Paper | Noise2Noise: Learning Image Restoration without Clean Data
Noise2Noise: Learning Image Restoration without Clean Data
发表在2018 ICML。
摘要:
We apply basic statistical reasoning to signal reconstruction by machine learning – learning to map corrupted observations to clean signals – with a simple and powerful conclusion: it is possible to learn to restore images by only looking at corrupted examples, at performance at and sometimes exceeding training using clean data, without explicit image priors or likelihood models of the corruption. In practice, we show that a single model learns photographic noise removal, denoising synthetic Monte Carlo images, and reconstruction of undersampled MRI scans – all corrupted by different processes – based on noisy data only.
结论:
We have shown that simple statistical arguments lead to new capabilities in learned signal recovery using deep neural networks; it is possible to recover signals under complex corruptions without observing clean signals, without an explicit statistical characterization of the noise or other corruption, at performance levels equal or close to using clean target data. That clean data is not necessary for denoising is not a new observation: indeed, consider, for instance, the classic BM3D algorithm (Dabov et al., 2007) that draws on self-similar patches within a single noisy image. We show that the previously-demonstrated high restoration performance of deep neural networks can likewise be achieved entirely without clean data, all based on the same general-purpose deep convolutional model. This points the way to significant benefits in many applications by removing the need for potentially strenuous collection of clean data.
AmbientGAN (Ashish Bora, 2018) trains generative adversarial networks (Goodfellow et al., 2014) using corrupted observations. In contrast to our approach, AmbientGAN needs an explicit forward model of the corruption. We find combining ideas along both paths intriguing.
要点:
- 以往我们都是学习受损图像到干净图像的映射;由于往往是病态问题,因此需要图像先验或似然模型。本文向我们展示:我们可以只通过观察受损样本,达到相似甚至更好的效果。本文以去噪为例。
- 实际上,这种思想在历史工作中已经有所体现。例如BM3D算法,通过搜索和处理同一张有噪图像内的相似块(没借助干净块),完成去噪的目的。但本文是第一个论证:这种思想也可以在DNN中实现。
优点:
- 这是一篇非常具有insight的文章,指出了理解神经网络学习与点估计的相似性。
- 这种insight可以指导我们直接通过有噪数据训练神经网络,解决了无损图像获取困难的问题。
局限:论证很模糊,并且是在噪声零均值的假设下论述的。
故事背景
如果我们接触过图像(信号)恢复中基于模型(重建)的算法,我们就知道:其难点和麻烦的地方,在于对似然函数(降质模型)和图像先验(稀疏、平滑等)的建模。
而CNN很好地解决了这一问题,但需要大量的训练数据,通常是受损输入\(\hat{x}_i\)和干净目标\(y_i\),并且训练目标是最小化经验损失:
其中,\(f_{\theta}\)是参数化的映射(a parametric family of mappings),例如CNN。
获取大量干净数据是很困难的。例如,为了获得无噪图像,我们需要长曝光;为了获得MRI图像的完整采样,图像中不能有动态目标等。
这篇文章就告诉我们:其实我们只需要观察受损图像,就能学习该映射,有时甚至能学得更好。同其他基于CNN的学习方法一样,我们不需要对似然和先验作过多假设。
算法原理
点估计
假设我们有一组温度采样数据\((y_1, y_2, \dots)\)。我们希望在某种损失度量\(L\)下,得到温度估计值\(z\)(希望该损失最小):
如果采用\(L_2\)损失,那么估计值就是观测值的算术平均(批注:假设样本分布i.i.d.):
总结一下,点估计带有一些统计平均的性质。比如,我们可以简单地对多点采样的温度取平均,得到最终的估计温度。
神经网络算法与点估计的关系
回过头来,我们观察式1。乍一眼看,式1表达的是参数预测问题(不是简单地估计值,而是学习一个预测模型,服务千千万万的输入),式2是点估计问题,二者不是一个东西。
理想状况下,网络的优化方式如下(提供准确的先验和似然):
上式可以理解为:对于每一个样本\(x_i\),都在执行一次点估计。可以理解为:根据观测点\(y\),估计点\(z = f_{\theta}(x)\),而估计完成时,参数\(\theta\)就可以根据\(z\)推出(或者说二者本质是一样的)。
当然,这种论证是很粗糙的,但提供给我们一个非常有用的见解。我们考虑超分辨问题:这是一个典型的病态问题,因为高频信息在采样过程中丢掉了,而同一张LR图像可以对应大量的HR图像。
借助上述点估计思想,我们不难理解:神经网络实际上是将这些大量的、可能的HR图像做了一个统计平均(点估计的特性),因此\(L_2\)范数下超分辨图像常常被过度平滑。
这也能解释BM3D的成功本质!
核心思想
基于上述思考,我们可以很自然地思考:既然是统计平均,那么我们可以将干净图像\(y\)随意换成其他图像(信号),只要保证期望不变,那么也能得到我们想要的估计值\(z = f_{\theta}(x)\)(式3),进而得到不变的参数\(\theta\)(式4)!
换句话说,如果假设噪声零均值(或保证期望仍然是无噪图像的期望),那么我们就可以让神经网络的输入和监督都是有噪图像,学习的参数是一样的!
即:
其中,\(\hat{x}_i\)是有噪图像,\(\hat{y}_i\)也是有噪图像(\(y_i\)不一定要和\(x_i\)相同),\(y\)就是目标干净图像。
附录A.3.给出了一个证明,证明\(y_i\)和\(\hat{y}_i\)均值之间的误差与样本数量\(N\)有关;当\(N\)足够大时,该误差趋于0。
在一篇引用该文的论文中,\(\hat{x}_i\)和\(\hat{y}_i\)用的是同一幅干净图像、在同一噪声分布下分别独立产生的两幅图像。
回头品味
再回头品味一下。实际上,BM3D算法属于基于模型(重建)的算法,英文叫a model-based or reconstruction-based approach。BM3D通过块匹配和协同滤波的方式去噪,可以简单理解为统计平均取均值,从而消除噪声。
但是,这篇文章提出,神经网络算法也可以理解为统计平均。这种思想很前卫,也很不好理解,论证也很模糊。
我们原来对神经网络工作模式的理解大致如下:大量有噪图像 -> 表征图像本质的高维特征 -> 重建图像 <- 对应干净图像监督。
现在我们换个角度理解:大量有噪图像 -> 表征图像本质的高维特征 -> 大量重建图像 <- 另一组有噪图像监督(要求或假设总期望相同)
再理解:如果我们能将 神经网络的工作模式 理解为点估计,那么无论是估计干净图像,还是估计另一组有噪图像(期望仍是干净的),学习得到的模型仍然是一样的,估计得到的参数也是一致的。
怎么理解,见仁见智,欢迎评论区各路大神启发我~~
实验
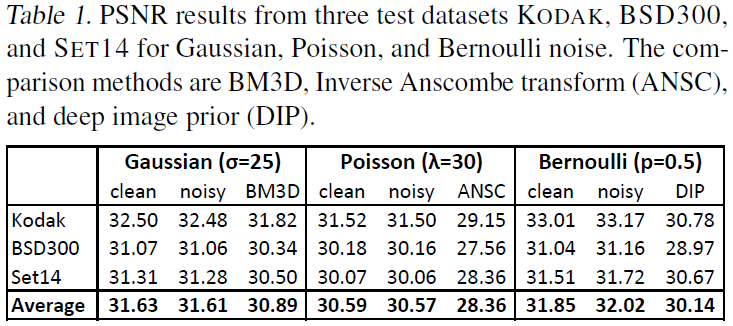
实验尝试了高斯噪声、泊松噪声、伯努利噪声、蒙特卡罗图像噪声,以及欠采样的MRI图像噪声。
高斯
网络采用RED30,是一个30层的残差网络。其余测试采用了更窄的U-Net,训练速度更快,效果相似。
高斯噪声标准差从0到50不等,混合在一个训练集中,因此让网络具有盲去噪的功能。
训练集采用ImageNet,测试集采用BSD300、SET14和KODAK。
如上表,该方法的效果超过了BM3D。
由于网络无法真正实现从一副有噪图像映射至另一幅有噪图像,因此损失一直都很大。
但是梯度不大,原因没看懂:
While the activation gradients are indeed noisy, the weight gradients are in fact relatively clean because Gaussian noise is independent and identically distributed (i.i.d.) in all pixels, and the weight gradients get averaged over \(2^16\) pixels in our fully convolutional network.
可能的意思是:平均多了,由于每个像素点上的噪声是iid的,因此会有一些抵消,故梯度比较干净。
但如果每个像素点之间的噪声存在关联,那么这种抑制效果就会减弱,梯度就会很大,训练会比较振荡。如下图(b):
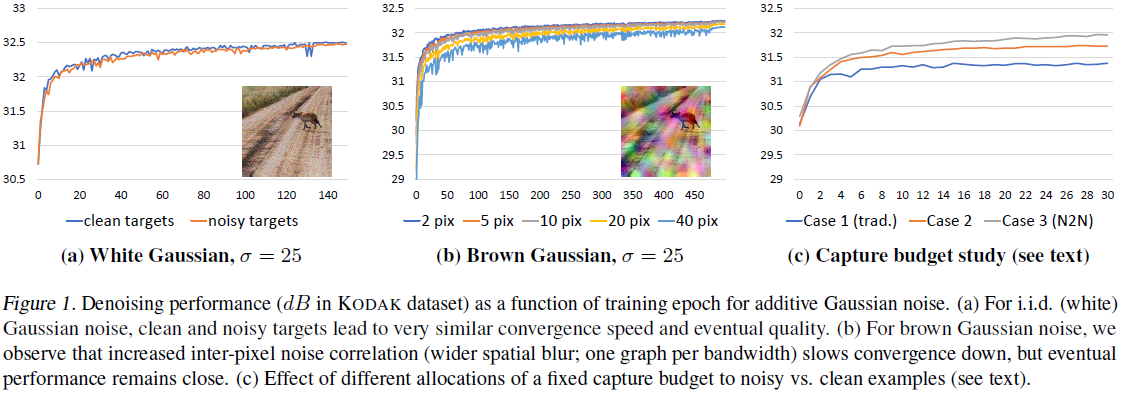
这种噪声是在高斯噪声图像的基础上,做了一个高斯滤波。带宽越大,关联越强,训练曲线越振荡。
现在,我们讨论算法对数据量的需求。假设使用一张ImageNet图像加噪,计算量是1CU。
-
第一种情况,我们使用100张图像,每张图像生成20副噪声图像。这样就有\(100*20*19 = 38000\)对训练样本。(噪声图像两两作为输入)
-
第二种情况,我们按照传统做法,100副图像,每幅图像生成1副对应的噪声图像,但训练时一一对应。
-
第三种情况,我们使用1000张图像,每张图像生成2副噪声图像。这样就有\(1000*2*1 = 2000\)对训练样本。
如上图(c),效果都比传统做法更好。
其他生成噪声
泊松噪声是摄像中的主要噪声,尽管是零均值的,但与信号有关,很难消除。略。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号