Paper | Non-local Neural Networks

Non-local Neural Networks

• Non-local Neural Networks
  • 1. 动机
  • 2. 相关工作
  • 3. Non-local神经网络
    • 3.1 Formulation
    • 3.2 具体实现形式
    • 3.3 Non-local块
  • 4. 视频分类模型
    • 4.1 2D ConvNet（C2D）
    • 4.2 膨胀的（inflated）3D ConvNet（I3D）
    • 4.3 Non-local network
  • 5. 实验

本文提出non-local操作来捕捉远距离依赖。受到Non-local[4]的启发，本文中一个位置的响应（response）是所有位置特征的加权求和。

1. 动机

• 对于序列数据（语音、语言、视频），远距离依赖性很重要，并且主要通过循环操作来建模远程依赖。

• 对于图像数据，上下文依赖性很重要，并且主要通过堆叠卷积层产生更大的感受野。

但是，这些操作效率都很低，并且能建模的远程依赖性也有限。

因此，本文提出了non-local操作，即将所有位置的特征加权求和，作为某个位置的响应。注意，这些“所有位置”可以是空间维度、时间维度或空间-时间维度，分别对应于图像、序列和视频。

我们注意图中\(x_i\)（球）。其实这个球与前面的所有位置都有关联，但图中只给出了关联性最高的位置。

2. 相关工作

Non-local是一种经典的滤波算法，即计算一张图像里所有像素值的加权平均。其后被用于BM3D，称为block matching技术。

实际上，non-local神经网络的本质是一种图神经网络（graph neural networks）[41]。

从另一个角度，non-local又与self-attention有异曲同工之妙。但self-attention主要用于机器翻译，而本文的网络用于更广泛的计算机视觉任务。

还有Interaction Networks，旨在建模多物体的相互关系[40,24]。

但non-local是以上工作的本质优势。【本文只能说提供了一种实现方式，没有特定目的，可以用于多种视觉任务】

3. Non-local神经网络

这一章行文蛮有意思的，先给出一个很简单的公式，然后举一大堆例子来完善这个公式。这是一种把简单的事物复杂化的写故事方法。

3.1 Formulation

本文定义的在神经网络中的non-local操作很简单：

\[y_i = \frac{1}{\mathcal{C}(x)} \sum_{\forall j} f(x_i, x_j) g(x_j) \]

其中\(y_i\)是输出，\(x_j\)是输入。\(i\)可以沿时间维度、空间维度或时间-空间维度遍历。\(f\)计算的是位置\(i\)和\(j\)的关系。\(\mathcal{C}\)是归一化函数。

我们可以对比一下卷积和循环操作：

• 卷积操作实际上是局部的non-local。例如\(3 \times 3\)卷积，就是一个在面积为9的邻域内的non-local操作，也符合上式。

• 循环操作也是局部的non-local，例如只考虑当前时刻和上一时刻。

• 全连接不是non-local。FC要求输入输出尺寸固定，并且是通过权值联系。而non-local输入尺寸随意，并且是通过函数学习相互联系。【博主认为FC是本文所示的non-local的特例】

3.2 具体实现形式

【本节点像在讨论attention的实现形式】

为了简洁，\(g\)用一个线性函数实现。即我们可以通过\(1 \times 1\)卷积或\(1 \times 1 \times 1\)卷积实现。以下讨论\(f\)的实现形式。实验将证明：以下选择不会对最终结果产生太大影响。

1. 高斯函数。在non-local mean[4]和双边滤波器[47]中使用的是欧氏距离，但为了方便运算，这里直接用点积：

   \[f(x_i, x_j) = \exp (x_i^T x_j) \]

   然后归一化函数就是\(\sum_{\forall j} f(x_j, x_i)\)。

2. 嵌入（embedded）高斯。

   \[f(x_i, x_j) = \exp ({\theta (x_i)}^T \phi (x_j)) \]

   无非就是在embedding空间上继续操作罢了。这里的\(\theta(x) = W_{\theta} x\)，\(\phi (x) = W_{\phi} x\)。归一化函数同上。

   有意思的是，这和attention is all you need里的self-attention本质一致。作者将这种联系强调为贡献：

   As such, our work provides insight by relating this recent self-attention model to the classic computer vision method of non-local means [4], and extends the sequential self-attention network in [49] to a generic space/spacetime non-local network for image/video recognition in computer vision.

3. 点积。即不再取e指数。此时归一化函数是常数\(N\)。为什么要归一化呢？因为输入尺寸未知。

   \[f(x_i, x_j) = {\theta (x_i)}^T \phi (x_j) \]

4. 拼接。

   \[f(x_i, x_j) = \text{ReLU} (w_f^T [\theta (x_i), \phi (x_j)]) \]

   归一化函数同上。

3.3 Non-local块

形式很简单：

\[z_i = W_z y_i + x_i \]

解释：\(y_i\)是习得的注意力，\(+ x_i\)即残差学习。【有意思，这又和residual attention networks异曲同工】

结合上一节，我们以embedding高斯为例，实现框图如图：

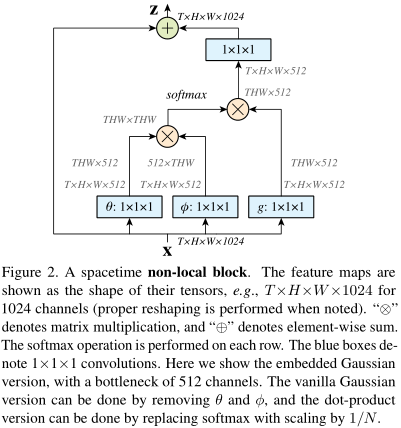
如果\(x\)有1024维度，那么\(W_{g,\theta,\phi}\)的维度都设为一半，即512。这样可以让注意力的计算量减小一半。最后\(W_{z}\)再升回去？

如果想降低计算量，有个简单做法：在\(\phi\)和\(g\)以后，做一次池化。即我们不考虑所有\(x_j\)，而只考虑一部分\(x_j\)。

4. 视频分类模型

有意思的是，本文的对比算法（baseline）也是作者搭建的。

4.1 2D ConvNet（C2D）

该baseline主要是为了探究时序信息的作用。C2D的时序操作是简单的池化，此外不考虑任何复杂操作。实现方式如表：

输入是32帧\(224 \times 224\)的视频。

4.2 膨胀的（inflated）3D ConvNet（I3D）

很简单。在C2D的基础上，把\(k \times k\)的2D卷积都改为\(t \times k \times k\)的3D卷积，即在某\(t\)帧上操作。

4.3 Non-local network

现在才是主菜。很简单，把non-local块加入上述的C2D和I3D就行了。作者同时考虑了加1个、5个和10个块的效果。

5. 实验

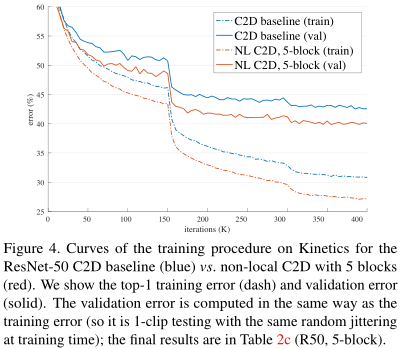
如图，无论是训练还是测试，加了NL块的网络都更快收敛，收敛得也更好。

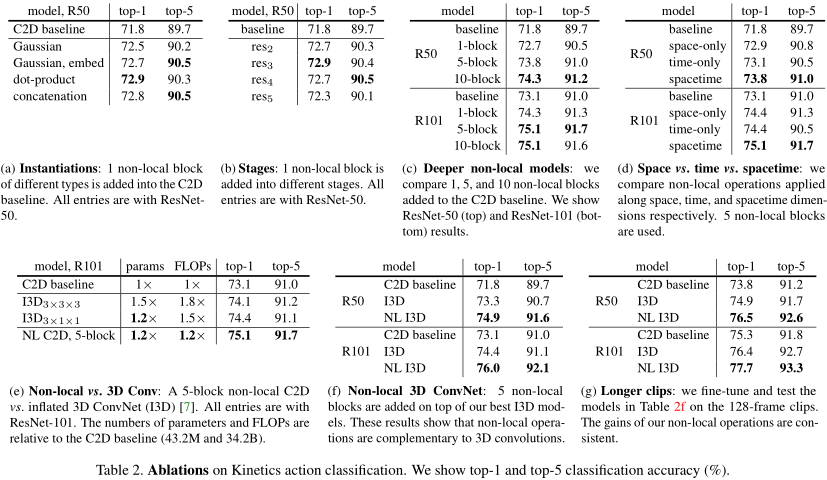
表(a)证实，上述几种attention方式在效果上没什么不同。

表(b)证实，attention block加在ResNet-50的五个块的任意一个块，性能上差异不大。加在最后一个块效果最差，可能是因为最后一个块采用了\(7 \times 7\)卷积，会导致注意力不精确。

表(c)证实，随着attention block的增加，性能在变好。这种性能增长并非是层数增长导致的。因为R50加10个block后，效果比R101不加block还好。

表(d)证实，如果只在空域或只在时间域上采用注意力机制，效果有提升但不大；同时在空域和时域采用注意力机制，效果最好。

表(e)证实，NL+C2D比I3D效果更好，并且FLOPs更少。参数差不多。

表(f)证实，I3D搭配NL效果也得到了提升。

表(g)证实，随着输入序列长度增加，NL的威力得到放大。

其他实验略。