Paper | Densely Connected Convolutional Networks

Densely Connected Convolutional Networks

• Densely Connected Convolutional Networks
  • 黄高老师190919在北航的报告听后感
  • 故事背景
  • 网络结构
    • Dense block
    • DenseNet
      • 过渡层
      • 成长率
      • 瓶颈层
      • 细节
  • 实验

发表在2017 CVPR。

摘要:

Recent work has shown that convolutional networks can be substantially deeper, more accurate, and efficient to train if they contain shorter connections between layers close to the input and those close to the output. In this paper, we embrace this observation and introduce the Dense Convolutional Network (DenseNet), which connects each layer to every other layer in a feed-forward fashion. Whereas traditional convolutional networks with L layers have L connections—one between each layer and its subsequent layer—our network has \(\frac{L(L+1)}{2}\) direct connections. For each layer, the feature-maps of all preceding layers are used as inputs, and its own feature-maps are used as inputs into all subsequent layers. DenseNets have several compelling advantages: they alleviate the vanishing-gradient problem, strengthen feature propagation, encourage feature reuse, and substantially reduce the number of parameters. We evaluate our proposed architecture on four highly competitive object recognition benchmark tasks (CIFAR-10, CIFAR-100, SVHN, and ImageNet). DenseNets obtain significant improvements over the state-of-the-art on most of them, whilst requiring less computation to achieve high performance. Code and pre-trained models are available at https://github.com/liuzhuang13/DenseNet.

结论:

We proposed a new convolutional network architecture, which we refer to as Dense Convolutional Network (DenseNet). It introduces direct connections between any two layers with the same feature-map size. We showed that DenseNets scale naturally to hundreds of layers, while exhibiting no optimization difficulties. In our experiments, DenseNets tend to yield consistent improvement in accuracy with growing number of parameters, without any signs of performance degradation or overfitting. Under multiple settings, it achieved state-of-the-art results across several highly competitive datasets. Moreover, DenseNets require substantially fewer parameters and less computation to achieve state-of-the-art performances. Because we adopted hyperparameter settings optimized for residual networks in our study, we believe that further gains in accuracy of DenseNets may be obtained by more detailed tuning of hyperparameters and learning rate schedules. Whilst following a simple connectivity rule, DenseNets naturally integrate the properties of identity mappings, deep supervision, and diversified depth. They allow feature reuse throughout the networks and can consequently learn more compact and, according to our experiments, more accurate models. Because of their compact internal representations and reduced feature redundancy, DenseNets may be good feature extractors for various computer vision tasks that build on convolutional features, e.g., [4, 5]. We plan to study such feature transfer with DenseNets in future work.

要点和优点:

• 稠密连接：每一层的输出特征图，都将作为其后所有层的输入。

• 网络可以深得多，优化难度却很低。

• 网络参数量更少，所需计算量大幅下降，性能却显著提升。

• 当提高参数量时，网络泛化能力也很好，不容易过拟合。

黄高老师190919在北航的报告听后感

一年前第一次看这篇文章时，感觉DenseNet无非是ResNet的一种极致扩展。但黄高老师给我提供了一种全新的思考。

我们首先看一个随机深度网络：如下图，在训练时，若干层会随机消失（由恒等变换或短路代替），在测试时再全部用起来。

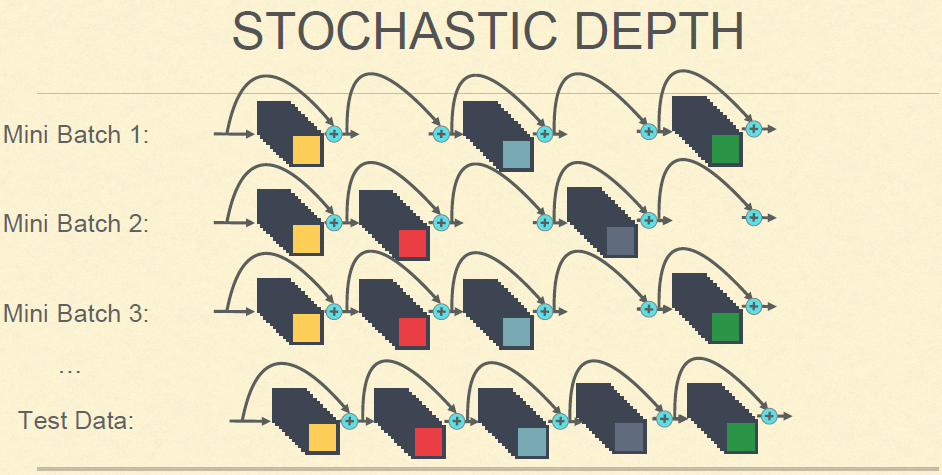
这个网络的泛化能力得到了显著提升。原因：这种类似于dropout形式的训练，迫使网络不会过于依赖于某一层。因为传统CNN是级联结构，黄老师认为，如果某一层出现问题，那么错误就会被逐级放大。因此这种随机深度+短路的形式，可以提升网络的泛化能力。

总之，我们应该看到以下两个矛盾：

那么，我们应该怎么取得权衡呢？
首先，我们应该保证网络的泛化能力，即引入适当的冗余。冗余不是臃肿，而是让网络不过度依赖某些参数或特征，从而具有一定的健壮性。短连接就是一个很好的方法，因为实验发现，大多数梯度传输都是通过短连接实现的。因此，黄老师就将此发挥到了极致：稠密连接。
其次，我们要尽量降低冗余。由于特征是稠密复用的，因此我们可以适当减少特征图数量，从而减少网络的整体参数量和计算量：我们大幅度减少每一层的特征图数量：

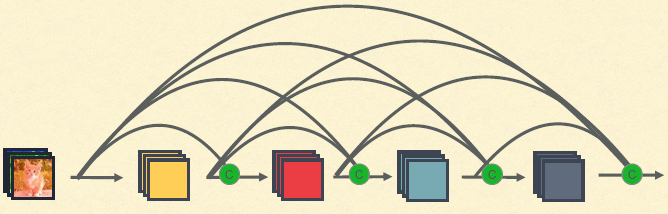
网络加深到121层（实验发现18层没有优势，因为特征图太少），参数量却低得多：

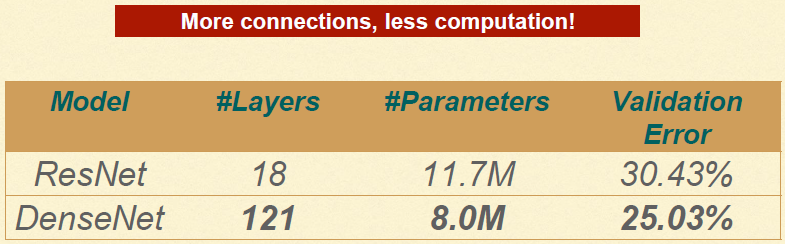
总之，如果我们将DenseNet理解为冗余与计算量的权衡，我们就对DenseNet有了更深层次的认知。

故事背景

尽管CNN已经发展了20多年，近期只有Highway Networks和ResNets突破了100层。

网络结构

Dense block

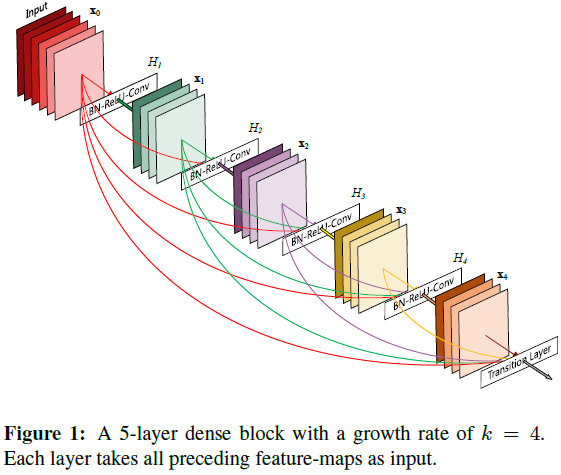
上图是一个示意图。注意，ResNet是将特征逐点求和，再输入下一层或输出，而这里DenseNet是将特征图通道拼接起来。同时注意，最后一层是过渡层（Transition Layer），也算在block内。

对于某个block内的第\(l\)个卷积层，其输入为\(l\)个输入的拼接。如果该block内一共有\(L\)层，那么一共就有\(l + (l-1) + \dots + 1 = (l + 1) \frac{l}{2}\)个连接。

DenseNet

我们看整体网络结构。在本文中，当通道拼接后，会依次执行BN、ReLU和\(3 \times 3\)的卷积。整体网络由多个block组成：

过渡层

还有一个问题。由于需要通道拼接，因此我们要保证特征图的尺寸相同。但显然这是很愚蠢的做法。为此我们有两点改进：

1. 引入block的概念，每一个block内稠密连接，block之间的尺寸不保证相同。

2. 为了完成block之间的过渡，作者引入了过渡层（transition layers），其包含BN、\(1 \times 1\)卷积以及\(2 \times 2\)的池化层。

在过渡层，我们让特征图数量减半（输出通道数等于输入通道数的一半）。这种设计以DenseNet-BC代替。

成长率

这种稠密连接的结构有一个反直觉的特点：其参数量（可以）非常小（批注：原因上一节我也提到了）。我们先看ResNet，它的参数量很大，原因是每一层的特征图都比较多也比较庞大。而对于DenseNet，每一层的特征图只限定为很小的数目，比如每层12张。作者称该超参数为成长率（growth rate）\(k\)。实验证明较小的成长率是足够的。

瓶颈层

尽管特征图数量\(k\)不大，但是拼接后的特征图数量还是太大了。为此，我们引入瓶颈层（bottleneck layers），即\(1 \times 1\)卷积层，在保证特征图尺寸不变的条件下，减小特征图数目。具体做法：在拼接后、BN+ReLU-\(3 \times 3\)Conv之前，加入BN+ReLU+\(1 \times 1\)Conv，即最终变成BN - ReLU - Conv (\(1\times 1\)) - BN - ReLU - Conv (\(3 \times 3\))。本文采用DenseNet-B表示这一结构，并通过实验证明其优势。

细节

• DenseNet中一共有3个dense block，每一个block内的特征图尺寸分别是\(32 \times 32\)、\(16 \times 16\)和\(8 \times 8\)。

• 在最开始，\(3 \times 3\)的卷积作用于输入图像，得到16通道的特征图，再输入第一个dense block。

• 对于\(3 \times 3\)卷积，两侧分别插一个零，保证特征图尺寸不变。

• 在过渡层，\(1 \times 1\)卷积搭配\(2 \times 2\)平均池化，如上图。

• 一个全局平均池化和softmax分类器搭载在最后一层之上，得到分类结果。

• 作者尝试了40层+成长率12、100层+成长率24、250层+成长率24等。

在ImageNet上的实验，作者采用的网络配置如下：

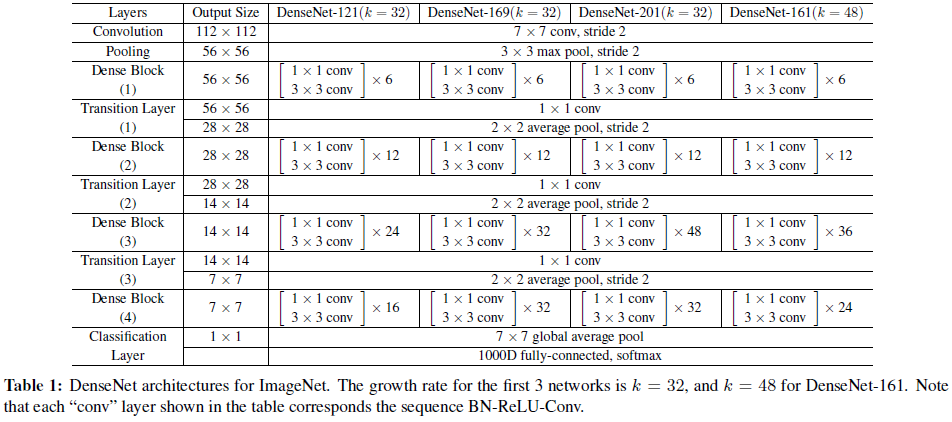
实验

我们主要看这个图：

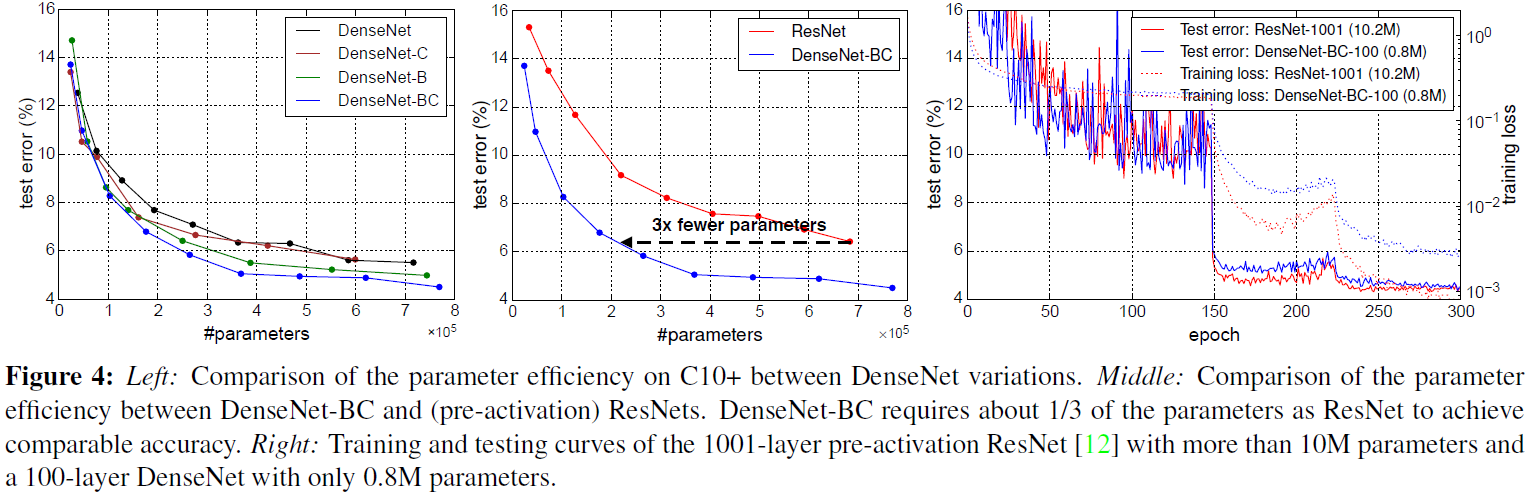
这表明：

• 稠密连接+瓶颈处理+过渡层压缩性能最佳。

• 与ResNet相比，DenseNet-BC不仅性能更好，参数量需求也更低。

• DenseNet泛化能力更好。虽然训练误差比ResNet高，但是测试效果是几乎一致的（在相同epoch条件下，与ResNet-1001相比）。