组合数学学习笔记

更好的阅读体验

update

2024-11-12 11:25 修改了一些格式错误且增加了二项式反演的例题

2024-11-12 14:33 改进了二项式反演的证明

基础知识

一、加法原理

完成某个工作有 \(n\) 类办法，第 \(i\) 类办法有 \(a_i\) 种，则完成此工作的方案数有 \(\sum\limits _{i=1}^n a_i\) 种。

二、乘法原理

完成某个工作有 \(n\) 个步骤，第 \(i\) 个步骤有 \(b_i\) 种，则完成此工作的方案数有 \(\prod\limits _{i=1}^n b_i\) 种。

排列组合（基础）

一、定义

1.排列数：从 \(n\) 个物体中选出 \(m\) 个物体按一定顺序排为一列的方案数，用 \(A_n ^m\ (\)或\(P_n^m)\) 表示，
\(A_n^m=\dfrac{n!}{(n-m)!}\)。

2.组合数：从 \(n\) 个物体种选出 \(m\) 个物体（不考虑顺序）的方案数，用 \(\begin{pmatrix} n \\ m \end{pmatrix}\)(或 \(C_n^m\))表示，\(\dbinom{n}{m}=\dfrac{A_n^m}{m!}=\dfrac{n!}{m!(n-m)!}\)。

3.插板法

现有 \(n\) 个完全相同的元素，要求将其分为 \(k\) 组。

• 保证每组至少有一个元素，一共有多少种分法？

考虑拿 \(k - 1\) 块板子插入到 \(n\) 个元素两两形成的 \(n - 1\) 个空里面。因为元素完全相同，所以答案就是 \(\dbinom{n - 1}{k - 1}\)。

本质是求 \(x_1+x_2+\cdots+x_k=n\) 的正整数解的组数。

• 每组允许为空，一共有多少种分法？

给总体先加上 \(k\) 个，以保证每组至少一个，接下来处理同上，最后相当于每组减一还回去即可。答案为 \(\dbinom{n+k-1}{k-1}\)。因为 \(\dbinom{n}{m}=\dbinom{n}{n-m}\),答案即为 \(\dbinom{n+k-1}{n}\)。

本质是求 \(x_1+x_2+\cdots+x_k=n\) 的非负整数解的组数。

• 对于第 \(i\) 组，至少要分到 \(a_i\) 个（\(\sum\limits a_i\le n\)），一共有多少种分法？

本质是求 \(x_1+x_2+\cdots+x_k=n\) 的整数解的组数。

模仿第三种情况，我们设 \(x'_i=x_i-a_i\) 以保证每组最少分到 \(a_i\) 个。现在相当于求 \(x'_1+x'_2+\cdots+x'_k=n\) 的整数解。

过程：

\[x'_1+x'_2+\cdots+x'_k=n \]

\[(x'_1+a_1)+(x'_2+a_2)+\cdots+(x'_k+a_k)=n \]

\[x_1+x_2+\cdots+x_k=n-a_1-a_2-\cdots-a_k \]

\[x_1+x_2+\cdots+x_k=n-\sum a_i \]

所以答案为 \(\dbinom{n-\sum a_i+k-1}{n-\sum a_i}\)。

---

例：\(\ \ 1 \sim n\) 这 \(n\) 个自然数中选 \(k\) 个，使得这 \(k\) 个数中任何两个数都不相邻的组合有 \(\dbinom {n-k+1}{k}\) 种。

证明：设选的 \(k\) 个数分别为 \(x_1,x_2,\cdots,x_k (x_1\le x_2\le \cdots \le x_k)\)，设 \(x'_i=x_i+i-1\)，则一定有 \(x'_1<x'_2<\cdots<x'_k\ \ (x'_k\le n)\)，即两两都不相邻。因为 \(x'_k=x_k+k-1\le n\)，所以 \(x_k\le n-k+1\)，我们只需在 \(1\sim n-k+1\) 中选 \(k\) 个数即可，答案为 \(\dbinom{n-k+1}{k}\) 种。

二项式定理

内容

\[(a+b)^n=\sum_{i=0}^n\binom{n}{i}a^{n-i}b^i \]

证明

采用数学归纳法。

先理解一个引理：帕斯卡法则，即：

\[\dbinom{n}{k}+\dbinom{n}{k-1}=\dbinom{n+1}{k} \]

• 证明帕斯卡法则：假设有 \(n+1\) 个人，要在其中选出 \(k\) 个人，很明显方案有 \(\dbinom{n+1}{k}\) 种；但不幸的是，一共的 \(n+1\) 个人中死了一个，现在我们总人数剩下 \(n\) 人，但还是要选 \(k\) 人，现在方案数为 \(\dbinom{n}{k-1}\) 种；我们发现少的方案数一定和那死的一个人有关，那我们所缺少的方案数就是在选种的 \(k\) 个人中有那个死人，所以我们还能自主选择 \(k-1\) 人，所以缺少的方案数为 \(\dbinom{n}{k-1}\)。所以我们有：

\[\dbinom{n+1}{k}-\dbinom{n}{k-1}=\dbinom{n}{k} \]

调换下顺序得到：

\[\dbinom{n}{k}+\dbinom{n}{k-1}=\dbinom{n+1}{k} \]

得证。

现在证明二项式定理。

当 \(n=1\) 时，原式显然成立。

假设当 \(n=k\) 时原式成立，设 \(n=k+1\)：

\[(a+b)^{k+1}=a(a+b)^k+b(a+b)^k \]

\[=a\sum_{i=0}^k\dbinom{k}{i}a^{k-i}b^i+b\sum_{j=0}^k\dbinom{k}{j}a^{k-j}b^j \]

将 \(a,b\) 乘进来：

\[=\sum_{i=0}^k\dbinom{k}{i}a^{k-i+1}b^i+\sum_{j=0}^k\dbinom{k}{j}a^{k-j}b^{j+1} \]

把前半部分 \(i=1\) 时提出来：

\[=a^{k+1}+\sum_{i=1}^k\dbinom{k}{i}a^{k-i}b^i+\sum_{j=0}^k\dbinom{k}{j}a^{k-j}b^{j+1} \]

将 \(j\) 化为 \(i-1\):

\[=a^{k+1}+\sum_{i=1}^k\dbinom{k}{i}a^{k-i}b^i+\sum_{i=1}^{k+1}\dbinom{k}{i-1}a^{k-i+1}b^{i} \]

把后半部分 \(i=k+1\) 时提出来：

\[=a^{k+1}+\sum_{i=1}^k\dbinom{k}{i}a^{k-i}b^i+\sum_{i=1}^{k}\dbinom{k}{i-1}a^{k-i+1}b^{i}+b^{k+1} \]

将中间两个求和合并：

\[=a^{k+1}+b^{k+1}+\sum_{i=1}^k\left[\dbinom{k}{i}+\dbinom{k}{i-1}\right]a^{k-i}b^i \]

套用帕斯卡法则：

\[=a^{k+1}+b^{k+1}+\sum_{i=1}^k\dbinom{k+1}{i}a^{k-i}b^i \]

\[=\sum_{i=0}^{k+1}\dbinom{k+1}{i}a^{k-i}b^i \]

所以当 \(n=k+1\) 时，结论仍成立。因此对任意 \(n\in \mathbb{N} ^{+}\)，均可使所证等式成立，
得证。

鸽巢原理（抽屉原理）

内容

将 \(n\) 个物体，划分为 \(k\) 组，那么至少存在一个分组，含有大于或等于 \(\left \lceil \dfrac{n}{k} \right \rceil\) 个物品。

证明

反证法。

设每个分组含有小于 \(\left \lceil \dfrac{n}{k} \right \rceil\) 个物体，则其总和 \(S\leq (\left \lceil \dfrac{n}{k} \right \rceil -1 ) \times k=k\left\lceil \dfrac{n}{k} \right\rceil-k < k(\dfrac{n}{k}+1)-k=n\) ，矛盾。

容斥原理

内容

设 \(U\) 中元素有 \(n\) 种不同的属性，而第 \(i\) 种属性称为 \(P_i\)，拥有属性 \(P_i\) 的元素构成集合 \(S_i\)，那么

\[\left|\bigcup_{i=1}^{n}S_i\right|=\sum_{m=1}^n(-1)^{m-1}\sum_{a_i<a_{i+1} }\left|\bigcap_{i=1}^mS_{a_i}\right| \]

证明

数学归纳法，懒得写了以后填坑（）

卡特兰数

定义

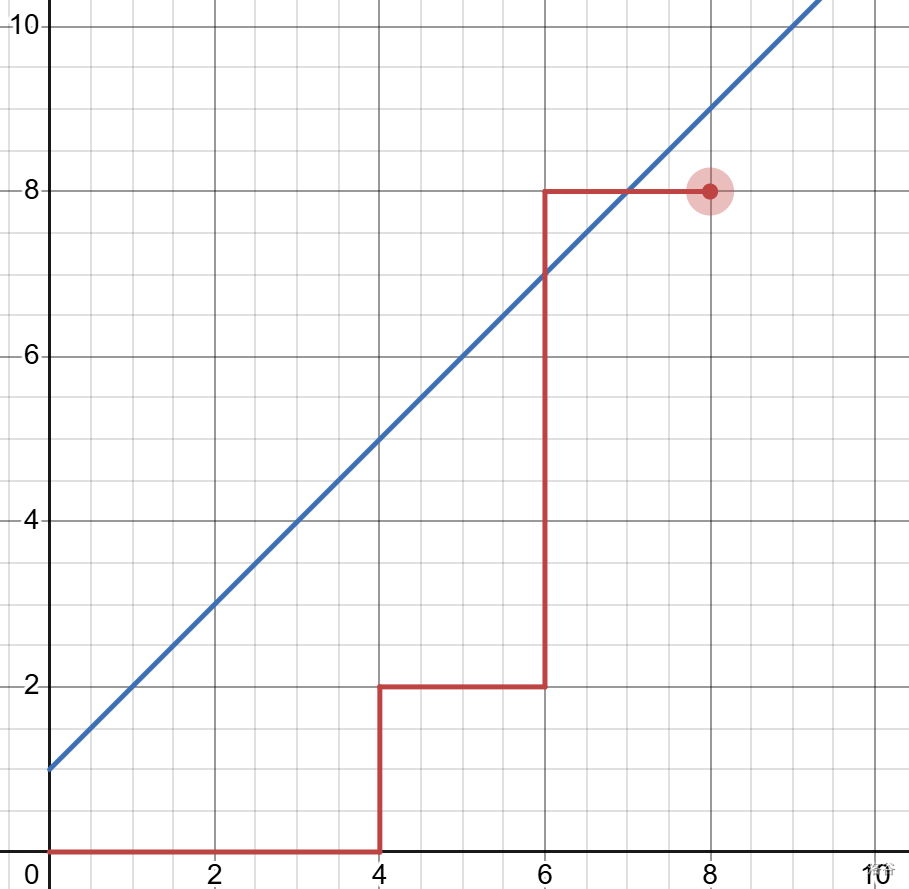
定义卡特兰数 \(H_n\) 表示坐标轴上从 \((0,0)\) 点到 \((n,n)\) 的路径中不越过直线 \(y=x\) 的路径数。下图为一种不合法的方案。

求法

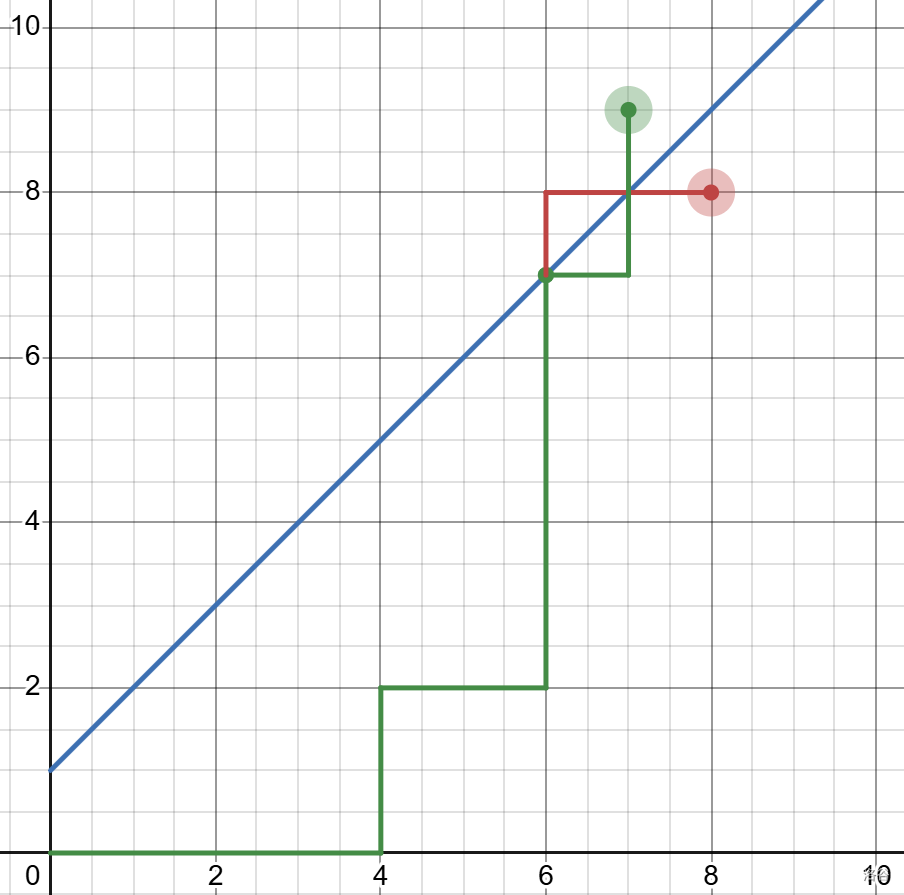
如下图，对每个非法的方案都可以通过把在第一个越过 \(y=x\) 的点之后的路径以直线 \(y=x+1\) 做对称从而构造一条自 \((0,0)\) 至 \((n-1,n+1)\) 的路径。

因为一共需要走 \(2n\) 步，所以从 \((0,0)\) 到 \((n,n)\) 的方案总数有 \(\dbinom{2n}{n}\) 种，从 \((0,0)\) 到 \((n-1,n+1)\) 的方案数有 \(\dbinom{2n}{n-1}\) 种。

综上可得：

\[\begin{aligned} H_n&=\dbinom{2n}{n}-\dbinom{2n}{n-1}\\ &=\frac{(2n)!}{(n!)^2}-\frac{(2n)!}{(n+1)!(n-1)!}\\ &=\frac{(n+1)(2n)!}{n!(n+1)!}-\frac{n(2n)!}{n!(n+1)!}\\ &=\frac{(2n)!}{n!(n+1)!}\\ &=\frac{\dbinom{2n}{n}}{n+1}\\ \end{aligned}\]

递推公式

\[H_n = \sum_{i=0}^{n-1}H_iH_{n-i-1} \]

\[H_n = \frac{4n-2}{n+1}H_{n-1} \]

证明：\((0,0)\) 到 \((n,n)\) 的路径可以分作以下几步：

• 从 \((0,0)\) 走到 \((i,i)\)，方案数为 \(H_i\)。

• 从 \((i,i)\) 走到 \((n-1,n-1)\)，方案数为 \(H_{n-i-1}\)。

• 从 \((n-1,n-1)\) 走到 \((n,n)\)，方案数为 \(1\)。

枚举每一个 \(i\)，由此得到 \(H_n = \sum_{i=0}^{n-1}H_iH_{n-i-1}\)。

\[\begin{aligned} & H_n = \frac{4n-2}{n+1}H_{n-1} \\ \iff & \frac{C_{2n}^n}{n+1} = \frac{4n-2}{n+1} \times \frac{C_{2n-2}^{n-1}}{n} \\ \iff & \frac{(2n)!}{(n+1)(n!)^2} = \frac{4n-2}{n+1} \times \frac{(2n-2)!}{n(n-1)!^2} \\ \iff & \frac{(2n)!}{n} = (4n-2) \times {(2n-2)!} \\ \iff & \frac{(2n)(2n-1)}{n} = 4n-2 \\ \iff & 4n-2 = 4n-2 \\ \end{aligned} \]

故得证。

组合数性质

性质1

\[\dbinom{n}{m}=\dbinom{n}{n-m} \]

证明

正确性显然，用组合数意义理解，在 \(n\) 个中选 \(m\) 个相当于在 \(n\) 个中挑 \(n-m\) 个不选。

性质2

\[\dbinom{n}{m}=\dfrac{n}{m}\dbinom{n-1}{m-1} \]

证明

\[\begin{aligned} \dbinom{n}{m}&=\dfrac{n!}{m!(n-m)!}\\ &=\dfrac{n}{m}\times \dfrac{(n-1)!}{(m-1)!(n-m)!}\\ &=\dfrac{n}{m}\dbinom{n-1}{m-1} \end{aligned}\]

性质3

\[\dbinom{n}{m}=\dbinom{n-1}{m}+\dbinom{n-1}{m-1} \]

证明

即帕斯卡定理的略微转换，具体见上。

性质4

\[\sum_{i=0}^{n}\dbinom{n}{i}=2^n \]

证明

将 \(a=b=1\) 带入二项式定理即可。

\[\begin{aligned} 2^n&=(1+1)^n\\ &=\sum_{i=0}^n\dbinom{n}{i}1^{n-i}1^i\\ &=\sum_{i=0}^n\dbinom{n}{i} \end{aligned}\]

性质5

\[\sum_{i=0}^{n}(-1)^i\dbinom{n}{i}=[n=0] \]

\([a]\) 表示当 \(a\) 为真时答案为 \(1\)，否则为 \(0\)（相当于一个 bool）。

证明

证法基本等同于性质 \(4\)，将 \(a=1,b=-1\) 带入二项式定理即可。

我们这里认为 \(0^0=1\)，所以 \(n=0\) 时答案为 \(1\)。

具体证明略。

性质6

\[\sum_{i=0}^{m}\dbinom{n}{i}\dbinom{m}{m-i}=\dbinom{n+m}{m}\tag{$n\ge m$} \]

证明

考虑通过组合数意义来理解。

假设现在有 \(n\) 个男生，\(m\) 个女生，我们现在要从这 \(n+m\) 个人中选出 \(m\) 个人，方案数显然为 \(\dbinom{n+m}{m}\)。另一种思考方式是从男生中选 \(i\) 个，女生中选 \(m-i\) 个，对于每个 \(i\) 方案数为 \(\dbinom{n}{i}\dbinom{m}{m-i}\)，枚举每个 \(i\) 即为总方案数。

性质7

\[\sum_{i=0}^n\binom{n}{i}^2=\binom{2n}{n} \]

证明

性质 \(6\) 的特殊情况，取 \(m=n\) 即可。

性质8

\[\sum_{i=0}^{n}i\dbinom{n}{i}=n2^{n-1} \]

证明

\[\begin{aligned} \sum_{i=1}^{n}i\dbinom{n}{i}&=n\cdot\sum_{i=1}^{n}\dfrac{i}{n}\dbinom{n}{i}\\ &=n\cdot\sum_{i=1}^{n}\dbinom{n-1}{i-1}\text{(套用性质2)}\\ &=n2^{n-1}\text{(套用性质4)}\\ \end{aligned}\]

性质9

\[\begin{aligned} \sum_{i=1}^{n}i^2\dbinom{n}{i}&=n(n+1)2^{n-2} \end{aligned}\]

证明

\[\begin{aligned} \sum_{i=1}^{n}i^2\dbinom{n}{i}&=n\cdot\sum_{i=1}^n\dfrac{i}{n}\dbinom{n}{i}\cdot i\\ &=n\cdot\sum_{i=1}^{n}i\dbinom{n-1}{i-1}\\ &=n\cdot\sum_{i=0}^{n-1}(i+1)\dbinom{n-1}{i}\\ &=n\cdot\sum_{i=0}^{n-1}i\dbinom{n-1}{i}+n\cdot\sum_{i=0}^{n-1}\dbinom{n-1}{i}\\ &=n\cdot\sum_{i=0}^{n-1}i\dbinom{n-1}{i}+n2^{n-1}\\ &=n(n-1)\cdot\sum_{i=0}^{n-1}\dfrac{i}{n-1}\dbinom{n-1}{i}+n2^{n-1}\\ &=n(n-1)\cdot\sum_{i=1}^{n-1}\dbinom{n-2}{i-1}+n2^{n-1}\\ &=n(n-1)2^{n-2}+n2^{n-1}\\ &=n(n+1)2^{n-2} \end{aligned}\]

拓展：求证 $$\begin{aligned}
\sum_{i=1}^{n}im\dbinom{n}{i}&=n^{{\overline{m}}2}
\end{aligned}$$。

性质10：

\[\binom{n}{r}\binom{r}{k} = \binom{n}{k}\binom{n-k}{r-k} \]

证明

\[\begin{aligned} \binom{n}{r}\binom{r}{k} &= \dfrac{n!}{r!(n-r)!}\cdot\dfrac{r!}{k!(r-k)!}\\ &= \dfrac{n!}{(n-r)!\cdot k!\cdot(r-k)!}\\ &= \dfrac{n!(n-k)!}{(n-r)!\cdot k!\cdot (r-k)!\cdot(n-k)!}\\ &=\dfrac{n!}{k!(n-k)!}\cdot \dfrac{(n-k)!}{(r-k)!(n-r)!}\\ &=\dbinom{n}{k}\dbinom{n-k}{r-k} \end{aligned}\]

二项式反演

内容

形式1

\[F_n=\sum_{i=0}^{n}(-1)^i{n\choose i}G_i \iff G_n=\sum_{i=0}^{n}(-1)^{i}{n\choose i}F_i \]

形式2

\[F_n=\sum_{i=0}^{n}{n\choose i}G_i \iff G_n=\sum_{i=0}^{n}(-1)^{n-i}{n\choose i}F_i \]

证明

发现形式一的形态很对称，那我们设一个反演系数。

设矩阵 \(A_{n,i}=(-1)^i\begin{pmatrix} n \\ i \end{pmatrix}\)，现在变为求证 $$F_n=\sum_{i=0}^{n}A_{n,i}G_i \iff G_n=\sum_{i=0}^{n}A_{n,i}F_i$$，即证 \(A*A=I\)。

\[\begin{aligned} (A*A)_{n,m}&=\sum_{t=1}^{\infty}{A_{n,t}}{A_{t,m}}\\ &=\sum_{t=m}^{n}(-1)^t{n \choose t}(-1)^m{t \choose m}\\ &=(-1)^m\sum_{t=m}^{n}(-1)^t{n \choose t}{t \choose m}\\ &=(-1)^m\sum_{t=m}^{n}(-1)^t(\dfrac{n!}{t!\times (n-t)!}\cdot\dfrac{t!}{m!\times (t-m)!})\\ &=(-1)^m\sum_{t=m}^{n}(-1)^t{n \choose m}{n-m \choose n-t}\\ &=(-1)^m{n \choose m}\sum_{t=m}^{n}(-1)^t{n-m \choose n-t}\\ &=(-1)^m{n \choose m}\sum_{t=0}^{n-m}(-1)^{t+m}+{n-m \choose n-t-m}\\ &=(-1)^{2m}{n \choose m}\sum_{t=0}^{n-m}(-1)^t+{n-m \choose t}\\ \end{aligned}\]

发现后面的那块是二项式定理，所以原式可以化简为：

\[(-1)^{2m}{n \choose m}(1-1)^{n-m} \]

仔细观察，此式只有在 \(n=m\) 时值为 \(1\)，其余时间都为 \(0\)，即 \([n=m]\)，也就是单位矩阵 \(I\)。

由此得证 \(A*A=I\) 即矩阵 \(A\) 自逆，从而得证形式一，而形式二通过移动 \(-1\) 的次幂即可推得。

例题

CF997C Sky Full of Stars

虽然 Codeforces 题库炸了，但不影响这是一道能用来练二项式反演的好题（好像也可以用容斥原理做？）。

套路化的，我们设 \(F_{i,j}\) 为 至少 有 \(i\) 行 \(j\) 列同色的方案数，\(G_{i,j}\) 为 恰好 有 \(i\) 行 \(j\) 列同色的方案数。很明显，我们有：

\[F_{x,y}=\sum_{i=x}^n\sum_{j=y}^n {n\choose i}{n\choose j}G_{i,j} \]

发现这是 二维二项式反演 的经典式子，反演后可得：

\[G_{x,y}=\sum_{i=x}^n\sum_{j=y}^n (-1)^{n-i}{n\choose i}(-1)^{n-j}{n\choose j}F_{i,j} \]

\[G_{x,y}=(-1)^{2n}\sum_{i=x}^n\sum_{j=y}^n (-1)^{i+j}{n\choose i}{n\choose j}F_{i,j} \]

而我们要求的答案是总方案数 \(3^{n^2}-G_{0,0}\)，问题即转化为求 \(F\)，接下来分类讨论。

• 当 \(ij \ne 0\) 时，同色的行和列一定交叉，所以所有行和列都是一种颜色，方案数为 \({n\choose i}{n\choose j}3^{(n-i)(n-j)+1}\)。
• 当 \(ij = 0,i+j \ne 0\) 时，同色的行和列一定交叉，所以所有行和列都是一种颜色，方案数为 \({n\choose i+j}3^{i+j+(n-i-j)n}\)。
• 当 \(i+j = 0\) 时，无限制，方案数为 \(3^{n^2}\)。

把 \(F\) 带回去算出 \(G_{0,0}\) 用全部方案数一减即可。