题解：CF1551D1 Domino (easy version)

题解：CF1551D1 Domino (easy version)

分析

题目中保证 $n\times m$ 为偶数，下面进行分类讨论。

情况一

如果 $n$ 和 $m$ 都是偶数，那么可以分割成 $\frac{n}{2}\times \frac{m}{2}$ 个 $2\times 2$ 的方块。

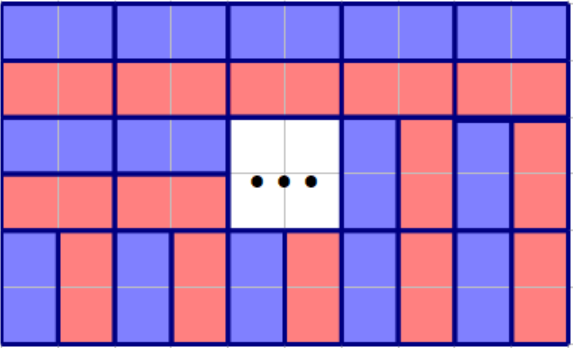
根据上图我们发现，只要 $k$ 满足 $0\le k\le \frac{n}{2}\times \frac{m}{2}\times 2$ 且 $2\mid k$，就一定可以凑出来。

情况二

如果 $n$ 是奇数，$m$ 是偶数，我们考虑把 $n$ 变为偶数转化为第一种情况。

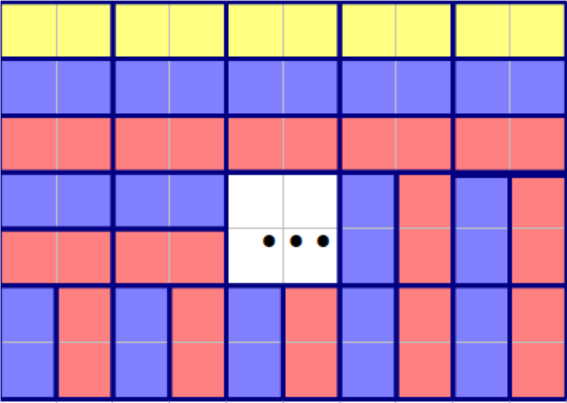
如上图，可以先在第一行排 $\frac{m}{2}$ 个多米诺骨牌，这时如果 $k<\frac{m}{2}$ 就无解，否则就直接转化为了第一种情况，此时 $k$ 变为 $k-\frac{m}{2}$。

情况三

如果 $n$ 是偶数，$m$ 是奇数，我们考虑把 $m$ 变为偶数转化为第一种情况。

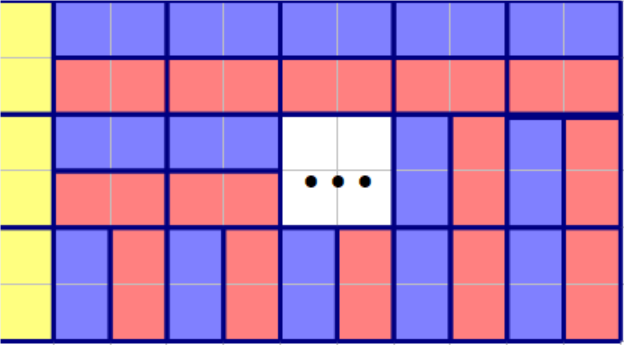
如上图，可以先在第一列排 $\frac{n}{2}$ 个多米诺骨牌。由于 $k$ 的限制是横向的多米诺骨牌，所以 $k$ 不变，转换为情况一。

代码

#include<bits/stdc++.h>
using namespace std;
int n,m,k;
bool check(int a,int b,int c)
{
    if(c&1)return 0;
    if(c>(a/2)*(b/2)*2)return 0;
    return 1;
}
signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int T;
    cin>>T;
    while(T--)
    {
        cin>>n>>m>>k;
        if(!(n&1)&&!(m&1))
        {
            if(check(n,m,k))
                cout<<"YES"<<endl;
            else
                cout<<"NO"<<endl;
        }
        else if((n&1)&&!(m&1))
        {
            if(k<m/2)
            {
                cout<<"NO"<<endl;
                continue;
            }
            k-=m/2;
            n--;
            if(check(n,m,k))
                cout<<"YES"<<endl;
            else
                cout<<"NO"<<endl;
        }
        else if(!(n&1)&&(m&1))
        {
            m--;
            if(check(n,m,k))
                cout<<"YES"<<endl;
            else
                cout<<"NO"<<endl;
        }
    }
    return 0;
}