二叉树前中后序与表达式的延伸
今天给大家讲一讲理论知识
二叉树之前中后序
二叉树基本定义
直白的讲,二叉树只由三部分组成:根,左子树,右子树
但是,每个左子树与右子树同样也可以把自己看作根,因此,他们也有自己的左子树与右子树
注:左子树与右子树可以为空气
二叉树前中后序
前中后序是三种遍历二叉树不同的方式
前序顺序:根 左 右
中序顺序:左 根 右
后序顺序:左 右 根
下面举个例子:
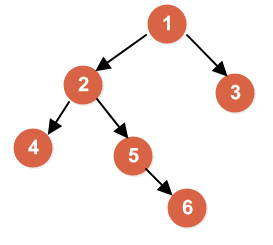 图片转载自风一样的码农的博客
图片转载自风一样的码农的博客
这个例子的三种顺序分别是:
前序:124563
中序:425613
后序:465231
前中后序在表达式中的使用
表达式分为前中后缀形式
其中,前中后缀形式等同于二叉树的前中后序
首先,人的大脑是中序,因此,我们可以将表达式通过二叉树的形式表现出来,然后再求此表达式的其他形式。
举个例子:
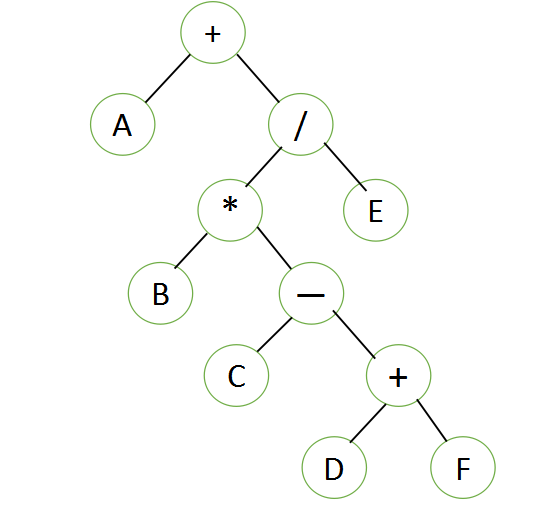
此表达式在我们人脑中应是(中序):A+B*[C-(D+F)]/E
前序:+A/*B-C+DFE
后序:ABCDF+-*E/+
计算机怎样求表达式
计算机很死板,它不可能看得懂我们人类的括号。
因此,计算机只能讲我们人类的中缀表达式改成后缀表达式,
然后,将他们从前往后放入栈中,如果入栈的是符号,则弹出它即比它早进栈的两位并将它们和刚入栈的符号进行运算,然后将结果放入栈。
还用刚刚的例子:ABCDF+-*E/+
设一个栈a,弹入与弹出过程如下:
1.A
2.A B 弹入字母,不进行操作
3.A B C
4.A B C D
5.A B C D F
6.A B C D F + 弹入“+”,弹出“+”,“D”,“F”,并求出D+F然后重新弹入结果
7.A B C D+F - 弹入“-”,弹出“-”,“C”,“D+F”,并求出C-(D+F)然后重新弹入结果
8.A B C-(D+F) * 弹入“*”,弹出“*”,“B”,“C-(D+F)”,并求出B*[C-(D+F)]然后重新弹入结果
9.A B*[C-(D+F)] E
10.A B*[C-(D+F)] E / 弹入“/”,弹出“/”,“B*[C-(D+F)]”,“E”,并求出B*[C-(D+F)]/E然后重新弹入结果
11.A B*[C-(D+F)]/E + 弹入“+”,弹出“+”,“A”,“B*[C-(D+F)]” ,并求出A+B*[C-(D+F)]然后重新弹入结果
运算结果为最终栈中的A+B*[C-(D+F)]
计算机通过后缀形式可以算出表达式
如果您觉得此博客还不错,别忘记点赞+关注


