【图论】长链剖分学习笔记
0x01：引入
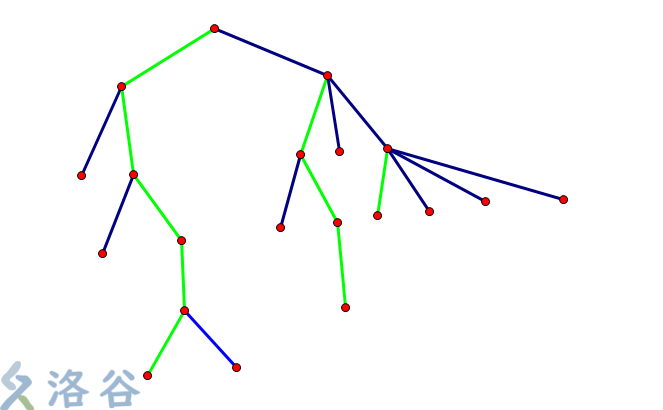
与重链剖分不同，长链剖分以子树深度最大的儿子作为重儿子，这里所述之深度是指子树内离它最远的叶子到它的距离。
如图绿色部分就是长链。
构造长链代码
点击查看代码
void dfs(int u,int fa){
for(int i=h[u];i;i=ne[i]){
int v=e[i];if(v==fa)continue;
dfs(v,u);
if(dep[v]>dep[son[u]])son[u]=v;
}
dep[u]=dep[son[u]]+1;
}
0x02：性质&结论
- 从根结点到任意叶子结点经过的轻边条数不超过 \(O(\sqrt{n})\)。
浅证：对于一个深度为 \(k\) 的结点，每往上跳一条轻边，其所在子树的结点个数至少增加 \(k+1\) 个。假设跳了 \(k\) 条轻边，其所在结点个数最少为 \(\sum_{i=1}^{k}i=\frac{k(k+1)}{2}\)。故得证。
- 一个结点的 \(k\) 级祖先所在长链长度一定不小于 \(k\)。
浅证：反证法。若小于 \(k\)，从长链的定义上看，应选择该结点所在子树作为重儿子。
- 选一个节点能覆盖它到根的所有节点。选 \(k\) 个节点，覆盖的最多节点数就是前 \(k\) 条长链长度之和，选择的节点即 \(k\) 条长链末端。
0x03：应用1：树上 k 级祖先
运用长链剖分可以做到 \(O(n\log n)\) 预处理，\(O(1)\) 查询。具体是这样的：
对于每个结点，预处理倍增数组。
对于每条长链的链顶，设链长为 \(k\)，则记录其向上/向下各 \(k\) 个结点。
查询时，先跳到 \(2^{\log k}\) 级祖先，由性质 2，再跳到链顶直接查表。
点击查看代码
void dfs1(int u){
d[u]=d[fa[u][0]]+1;
for(int i=1;i<=19;++i)
fa[u][i]=fa[fa[u][i-1]][i-1];
for(int i=h[u];i;i=ne[i]){
int v=e[i];
dfs1(v);
if(dep[v]>dep[son[u]])son[u]=v;
}
dep[u]=dep[son[u]]+1;
}
void dfs2(int u,int t){
top[u]=t;down[t].push_back(u);
if(u==t){
for(int i=0,p=u;i<=dep[u];++i){
up[u].push_back(p);
p=fa[p][0];
}
}
if(son[u])dfs2(son[u],t);
for(int i=h[u];i;i=ne[i]){
int v=e[i];if(v==son[u])continue;
dfs2(v,v);
}
}
int query(int u,int k){
if(!k)return u;
u=fa[u][lg[k]],k-=1<<lg[k];
k-=d[u]-d[top[u]],u=top[u];
return k>=0?up[u][k]:down[u][-k];
}
0x04：应用2：优化 dp
长链剖分可以优化深度相关的 dp，形如 \(f_{u,k}\) 表示以 \(u\) 为根且深度为 \(k\) 的答案（这里的深度就是深度，不是定义里那个），其思路与 dsu on tree 类似：先遍历重儿子并继承重儿子的答案，然后遍历并合并轻儿子的答案。
设 \(f_{u,k}\) 表示 \(u\) 子树中到 \(u\) 距离为 \(k\) 的结点个数，显然有
然而空间时间双炸，考虑优化，就是上面那个做法。
注意到每个点只会被合并一次，因为当 \(u\) 所在链顶 \(t\) 与 \(fa_t\) 合并时，\(u\) 的答案已经在 \(t\) 里面了，于是时间复杂度是 \(O(n)\) 的。
但是，光继承重儿子的答案就得是 \(O(n)\) 的啊。接下来就是长链剖分最美妙的地方：
注意到，若我们继承重儿子 \(v\) 的答案，有 \(f_{u,k}=f_{v,k+1}\)，也就是平移了一个位置。
那么，对每一条长链，分配一个内存空间让链上的点共用不就行了，也就是给每个结点动态地分配一个指针。这样空间和时间都变成了 \(O(n)\)。
点击查看代码
const int N=1e6+10;
//f[u][i]表示以u为根的子树内距离为i的结点数
int buf[N],*now=buf;//统一的内存条，now指针维护一段连续内存的起始地址
int n,ans[N],*f[N];//同一条长链中的结点共享一段连续的内存(长度为长链长)
int h[N],e[N<<1],ne[N<<1],idx;
int dep[N],son[N];//长链剖分用
void add(int a,int b){e[++idx]=b,ne[idx]=h[a],h[a]=idx;}
void dfs1(int u,int fa){
for(int i=h[u];i;i=ne[i]){
int v=e[i];if(v==fa)continue;
dfs1(v,u);
if(dep[v]>dep[son[u]])son[u]=v;
}
dep[u]=dep[son[u]]+1;
}
void dfs2(int u,int fa){
f[u][0]=1;
if(son[u]){
f[son[u]]=f[u]+1;//共享内存，但需平移一位，f[son[u]][dep]的信息就会相应存在f[u][dep+1]里,节省合并时间
dfs2(son[u],u);
ans[u]=ans[son[u]]+1;//继承son[u]答案
}
for(int i=h[u];i;i=ne[i]){//合并轻子树答案
int v=e[i];if(v==fa||v==son[u])continue;
f[v]=now,now+=dep[v];//分配内存,平移(此时v为所在重链链顶)
dfs2(v,u);
for(int j=1;j<=dep[v]+1;++j){
f[u][j]+=f[v][j-1];
if(f[u][j]>f[u][ans[u]]||(f[u][j]==f[u][ans[u]]&&j<ans[u]))ans[u]=j;
}
}
if(f[u][ans[u]]==1)ans[u]=0;
}
int main(){
#ifdef LOCAL
freopen("std.in","r",stdin);
freopen("my.out","w",stdout);
#endif
read(n);
for(int i=1,a,b;i<n;++i){
read(a),read(b);
add(a,b),add(b,a);
}
dfs1(1,0);
f[1]=now,now+=dep[1];//分配地址，同时将指针平移
dfs2(1,0);
for(int i=1;i<=n;++i)printf("%d\n",ans[i]);
return 0;
}
0x05：其他例题
调了一天代码，写你妈的长剖，给我写 dsu on tree 去。
