构造题做
-
找出题中特殊限制(前提)
-
找出答案的限制(求出的方法?取值范围?性质?若需判断能否构造,条件是什么?...)
-
贪心(关键):逐一解决限制
CF1712D Empty Graph
-
\(n\) 个点的完全图,\(l,r\) 之间的边权为 \(\min_{i=l}^r a_i\)。
-
由于是完全图,则任意两点都存在边,两点之间的最短路只有两种情况:直接走;通过 \(a_{min}\) 的点走,即 \(d(u,v)=\min(e(u,v),e(u,k_{min})+e(k_{min},v))=\min(\min_{i=l}^ra_i,2\times a_{min})\)。
-
注意到 \(e(l,r)\ge e(l+1,r)\),这告诉我们只用考虑编号相邻两点即可。于是整个直径就是 \(\max(\min(a_i,a_{i+1},2\times a_{min}))\)。看到 \(max,min\) 相互嵌套果断二分答案。首先解决 \(a_{min}\) 的限制,若 \(2\times a_i<mid\) 显然要把 \(a_i\) 变大。然后解决 \(\min(a_i,a_{i+1})\),如果存在 \(\ge mid\) 的那没事了,若没有,则考虑是否有 \(a_i\ge mid\),有则随便修改一条它相邻的边(点),无则要修改两个点。判断总修改次数是否 \(\le k\) 即可。
点击查看代码
const int N=1e5+10,inf=1e9;
int n,k,a[N],tmp[N];
bool check(int mid){
int tot=0,qwq=-1;bool flag=0;
for(int i=1;i<=n;++i){
if(2*a[i]<mid)tmp[i]=inf,++tot;
else tmp[i]=a[i];
}
for(int i=1;i<n;++i){
if(min(tmp[i],tmp[i+1])>=mid){flag=1;break;}
qwq=max(qwq,tmp[i]);
}qwq=max(qwq,tmp[n]);
if(flag)return tot<=k;
return (qwq>=mid?tot+1:tot+2)<=k;
}
void solve(){
read(n),read(k);
for(int i=1;i<=n;++i)read(a[i]);
int l=1,r=1e9,mid,ans;
while(l<=r){
mid=(l+r)>>1;
if(check(mid))ans=mid,l=mid+1;
else r=mid-1;
}
printf("%d\n",ans);
}
int main(){
int t;read(t);
while(t--)solve();
return 0;
}
CF1717D Madoka and The Corruption Scheme
-
比赛是二叉树的形式,可以钦定比赛对手,可以钦定赢家,但是某场比赛的赢家会被改变(只有 \(k\) 次)。
-
在会被改变的情况下,求能保证的编号最小。
-
既然我们能钦定一开始的排列顺序以及谁赢,不如我们把他直接确定下来,
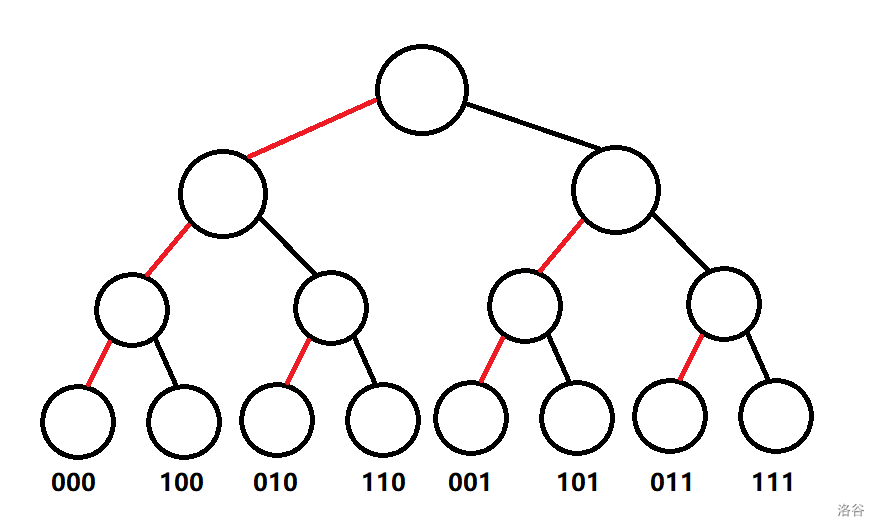
红边表示钦定它赢,用 0 表示该边赢,1 表示该边输,则叶子节点都对应一个唯一的 01 串。全为 0 的那位就是最后的赢家。
对于赞助商单次改变结果的操作相当于将某个节点的 1 变成 0。对于一个人,赞助商想要他赢,它的编号不能有多于 \(k\) 个 1。
于是我们可以算出赞助商能钦定的赢家个数 \(cnt\),我们从小到大安排编号,那么最终的答案就是 \(cnt\) 啦。
\(cnt\) 怎么算?编号的二进制位有 \(n\) 位,其中 \(i\) 位是 \(1\) 的人就有 \(\dbinom{n}{i}\) 个,答案就是 \(\sum_{i=0}^{\min(n,k)}\dbinom{n}{i}\)。
点击查看代码
const int N=1e5+10,mod=1e9+7;
int n,k;
long long fac[N],ifac[N],ans=0;
long long qpow(long long a,int b){
long long res=1;
while(b){
if(b&1)res=res*a%mod;
b>>=1;a=a*a%mod;
}
return res;
}
long long C(int a,int b){
return fac[a]*ifac[b]%mod*ifac[a-b]%mod;
}
int main(){
read(n),read(k);fac[0]=1;
for(int i=1;i<=n;++i)fac[i]=1ll*i*fac[i-1]%mod;
ifac[n]=qpow(fac[n],mod-2);
for(int i=n-1;~i;--i)ifac[i]=1ll*(i+1)*ifac[i+1]%mod;
for(int i=0;i<=min(n,k);++i)ans=(ans+C(n,i))%mod;
printf("%lld\n",ans);
return 0;
}
CF1381A2 Prefix Flip (Hard Version)
-
对于一次操作,是将前缀取反后反转。
-
最多操作 \(2n\) 次,使 \(a\) 变成 \(b\)。
-
注意到操作并不会影响到后缀,考虑从后往前逐位确定。对于一位 \(a_i\not= b_i\),则考虑能否通过反转前缀 \([1,i]\) 得到,若 \(a_1\not=b_i\),则先反转第一个数再反转 \([1,i]\)。故最多操作 \(2n\) 次,符合要求。记录一下前缀区间的 \(l,r\) 和反转情况就能很好维护了。
点击查看代码
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
#define pb push_back
const int N=1e5+10;
int n,a[N],b[N];
vector<int>ans;
void solve(){
scanf("%d",&n);ans.clear();
for(int i=1;i<=n;++i)scanf("%1d",&a[i]);
for(int i=1;i<=n;++i)scanf("%1d",&b[i]);
int l=1,r=n,rev=0;
for(int i=n;i;--i){
if((a[r]^rev)==b[i]){
l<r?--r:++r;
continue;
}
if((a[l]^rev)==b[i])ans.pb(1);
ans.pb(i);
swap(l,r),rev^=1;
l<r?--r:++r;
}
printf("%d ",ans.size());
for(int i:ans)printf("%d ",i);printf("\n");
}
int main(){
#ifdef LOCAL
freopen("std.in","r",stdin);
freopen("my.out","w",stdout);
#endif
int t;scanf("%d",&t);
while(t--)solve();
return 0;
}
CF1706D2 Chopping Carrots (Hard Version)
-
结果的式子中含有下取整,有 \(\max\) 和 \(\min\),\(1\le p_i\le k\)。
-
求 \(\max-\min\) 的最小值
-
可以考虑枚举最小值 \(v\in[0,a_1]\)(注意 \(a\) 是递增给出的,\(p_1=1\) 时取得上界 \(a_1\),下界显然是 \(0\)),对于 \(1\le i\le n\) 计算 $\max_{i=1}^n (\left\lfloor\frac{a_i}{p_i}\right\rfloor)-v $ 的最小值,其中 \(p_i\) 尽量大,这可以通过 \(p_i=\left\lfloor\frac{a_i}{v}\right\rfloor\) 得到。时间复杂度是 \(O(n\times a_1)\) 的,只能通过弱化版本。
这个做法的瓶颈就是对于枚举的每一个 \(v\) 都要 \(O(n)\) 算一遍能取到的最大值,考虑如何通过预处理优化这个过程。
记 \(maxn(v)\) 表示当取 \(v\) 为最小值时,取到的最大值,也就是上面 \(O(n)\) 算的东西。考虑每个 \(a_i\) 对其有什么影响。
注意到 \(\left\lfloor\frac{a_i}{p_i}\right\rfloor\) 的取值只有 \(O(\min(k,\sqrt{a_i}))\) 种(整除分块的结论),记为 \(s_1,s_2,...,s_x\),显然对于 \(s_j<v\le s_{j+1}\),\(maxn(v)\) 至少为 \(s_{j+1}\)。于是我们可以用 \(s_{j+1}\) 去更新 \(maxn(s_j+1)\),最后计算答案的时候扫描一遍就可以了。总共时间复杂度 \(O((\sum_{i=1}^n\min(k,\sqrt{a_i}))+a_1)\)。
点击查看代码
int n,k,a[N],maxn[N];
void solve(){
read(n),read(k);
memset(maxn,0,sizeof maxn);
for(int i=1;i<=n;++i){
read(a[i]);int pre=-1,cur;
//注意这里枚举取值是递减的,所以是用 pre 更新 cur+1
for(int j=1;j<=min(a[i],k);j=(a[i]/(a[i]/j))+1){
cur=a[i]/j;
maxn[cur+1]=max(maxn[cur+1],pre);
pre=cur;
}maxn[0]=max(maxn[0],pre);
}
int qwq=0,ans=1e9;
for(int i=0;i<=a[1];++i){
qwq=max(qwq,maxn[i]);
ans=min(ans,qwq-i);
}printf("%d\n",ans);
}
CF1738D Permutation Addicts
-
\(b\) 的构造与 \(a\) 和 \(k\) 存在大小关系,且 \(b\) 所代表的值在 \(a\) 前面,或为特殊值。
-
给出 \(b\),构造合法的 \(a\) 和 \(k\)。
-
写的太好了遂搬过来

点击查看代码
int n;
vector<int>e[N],ans;
void dfs(int u){
ans.pb(u);
for(int v:e[u])if(e[v].empty())ans.pb(v);
for(int v:e[u])if(!e[v].empty())dfs(v);
}
void solve(){
read(n);ans.clear();
for(int i=0;i<=n+1;++i)e[i].clear();
int k=N;
for(int i=1,b;i<=n;++i){
read(b);e[b].pb(i);
i<b?k=min(k,b-1):k=min(k,i-1);
}printf("%d\n",k);
if(!e[0].empty())dfs(0);
else dfs(n+1);
for(int i=1;i<=n;++i)printf("%d ",ans[i]);printf("\n");
}
CF1658C Shinju and the Lost Permutation
-
排列 \(p\) 的 \(i\) 循环置换表示将后 \(i\) 个数移到最前
-
定义 \(i\) 循环置换的权值为 \(\max_{j=1}^{k}p_j\) 的不同元素个数,给出 \(c_i\) 表示 \(i-1\) 循环置换的权值,是否存在排列 \(p\) 满足 \(c\)。
-
注意到若最大数 \(n\) 在最前面,则 \(c_i=1\),这样的 \(c_i\) 有且仅有一个。事实上 \(i-1\) 循环置换到 \(i\) 只是将最后一个数移到前面,于是我们从这个 \(1\) 的位置开始往后循环判断,可以分讨得出相邻两次置换一定得满足 \(c_i-c_{i-1}\le 1\)。
点击查看代码
const int N=1e5+10;
int n,c[N];
void solve(){
read(n);int flag=0,pos;
for(int i=1;i<=n;++i){
read(c[i]);
if(c[i]==1)pos=i,++flag;
}
if(flag>1||!flag)return printf("NO\n"),void();
for(int i=1;i<=n;++i){
int nxt=pos+1>n?1:pos+1;
if(c[nxt]-c[pos]>1){flag=0;break;}
pos=nxt;
}
if(!flag)printf("NO\n");
else printf("YES\n");
}
int main(){
#ifdef LOCAL
freopen("std.in","r",stdin);
freopen("my.out","w",stdout);
#endif
int t;read(t);
while(t--)solve();
return 0;
}
CF1691D Max GEQ Sum
1、2. 给出 \(a_i\) 询问对于所有的 \((1\le i<j\le n)\) 都满足 \(\max_{l=i}^j a_l\ge \sum_{l=i}^j a_l\)。
- 一种很自然的思路就是钦定某个数为最大值,向左右拓展判断最大的和是否小于等于它。向左右拓展可以用双向链表维护,从小到大钦定数之后删掉就可以了。
点击查看代码
const int N=2e5+10;
#define int long long
int n,a[N],sum[N],p[N];
int pre[N],nxt[N];
int lg[N],mn[20][N],mx[20][N];
void build(){
for(int i=1;i<=lg[n];++i){
for(int j=1;j+(1<<i)-1<=n;++j){
mn[i][j]=min(mn[i-1][j],mn[i-1][j+(1<<(i-1))]);
mx[i][j]=max(mx[i-1][j],mx[i-1][j+(1<<(i-1))]);
}
}
}
int query(int l,int mid,int r){
int p=lg[mid-l+1],q=lg[r-mid+1];
return max(mx[q][mid],mx[q][r-(1<<q)+1])-min(mn[p][l],mn[p][mid-(1<<p)+1]);
}
void solve(){
read(n);
for(int i=1;i<=n;++i){
read(a[i]);pre[i]=i-1,nxt[i]=i+1,p[i]=i;
sum[i]=sum[i-1]+a[i],mn[0][i]=sum[i-1],mx[0][i]=sum[i];
}build();
sort(p+1,p+n+1,[](const int &x,const int &y){return a[x]<a[y];});
for(int i=1;i<=n;++i){
int id=p[i];
if(a[id]<query(pre[id]+1,id,nxt[id]-1))return printf("NO\n"),void();
pre[nxt[id]]=pre[id];nxt[pre[id]]=nxt[id];
}printf("YES\n");
}
signed main(){
for(int i=2;i<N;++i)lg[i]=lg[i>>1]+1;
int t;read(t);
while(t--)solve();
return 0;
}
CF1659D Reverse Sort Sum
-
操作 \(i\) 得到的序列就是将 \(a\) 前 \(i\) 个数排序后的序列。\(c_i\) 表示 \(n\) 次操作每列的和。
-
给出 \(c_i\) 求 \(a_i\),保证有解。
-
一个显然的结论就是 \(a_i\) 里面每个 \(1\) 对 \(\sum c_i\) 都贡献了 \(n\) 次,于是 \(1\) 的个数就是 \(\frac{\sum c_i}{n}\)。由于每次操作都是和前缀有关,所以考虑从后往前推。
注意到,若序列存在 \(1\),则 \(c_n\) 要么是 \(n\) 要么是 \(1\),这分别对应 \(a_n=1\) 和 \(a_n=0\)。那我们可不可以用类似的结论推出 \(a_i\) 呢?当然是可以的。
若 \(a_i=1\),则它一定会在前 \(i\) 次操作内给 \(c_i\) 贡献 \(i\) 次。设当前在位置 \(i\),剩余 \(cnt\) 个 \(1\) 没填。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号