【DP】SOSdp 学习笔记
SOS（sum over subset），解决一类子集求和的 dp 问题。参考文章
给你一个长为 \(n\) 的序列 \(a\)，求 \(sum[S]=\sum_{i\subseteq S}a[i]\)，即子集求和。
你说那简单啊，\(O(3^{m})\) 枚举子集不就行了吗。（\(m\) 为最高位数）
点击查看代码
for (int S=0;S<(1<<n);++S){
sum[S]=a[0];
for(int i=S;i;i=(i-1)&S){
sum[S]+=a[i];
}
}
事实上，这样枚举子集也会有重复枚举的情况，还可以再继续优化。优化的方向就是减少枚举次数。
改变一下 \(sum[S]\) 的表示，变成 \(sum[S][j]=\sum_{i\subseteq S,S\oplus i<2^{j+1}}\ \ a[i]\)，即与其只有前 \(j\) 位不同的子集的和，这样我们可以把集合划分成互不相交的集合。容易写出 dp：
可以滚动数组，然后枚举 \(S\) 就行了。
点击查看代码
for(int i=0;i<(1<<N);++i)sum[i]=a[i];
for(int i=0;i<N;++i)for(int S=0;S<(1<<N);++S){
if(S&(1<<i))sum[S]+=sum[S^(1<<i)];
}
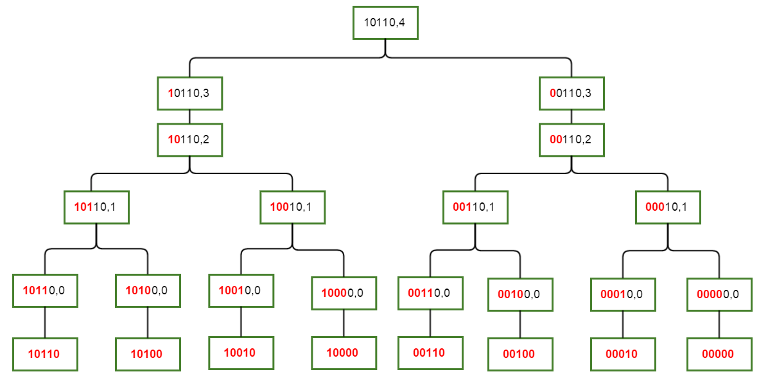
（原文图片，方便理解）
显而易见，这样的复杂度是 \(O(m2^m)\)（\(m\) 是位数）的。
\(\circ\) CF165E Compatible Numbers
给出一个序列 \(a\)，对于每个 \(a_i\) 问你是否存在 \(a_j\) 满足 \(a_i\& a_j=0\)，有则输出这个 \(a_j\)。
这里 \(a_j\) 并不是 \(a_i\) 的子集，怎么转移？注意到，\(a_j\) 是 \(a_i\) 补集的子集啊！于是我们还是按照求子集的方式去转移，询问的时候查询补集就行了。
点击查看代码
const int N=1e6+10,all=(1<<22)-1;//全集
int n,a[N],f[all+10];
int main(){
read(n);
memset(f,-1,sizeof f);
for(int i=1;i<=n;++i){
read(a[i]);
f[a[i]]=a[i];
}
for(int i=0;i<22;++i){//按正常子集转移
for(int S=0;S<=all;++S){
if((S&(1<<i))&&f[S^(1<<i)]!=-1)f[S]=f[S^(1<<i)];
}
}
for(int i=1;i<=n;++i)printf("%d ",f[all&(~a[i])]);//询问补集
return 0;
}
\(\circ\) CF449D Jzzhu and Numbers
给出序列 \(a\)，从 \(a\) 里面选出一个非空子集使这些数按位与起来为 \(0\)，求方案数。
好牛逼的题，考虑分析一下条件。
按位与为 \(0\)，也就是说对每一位都至少有一个数是 \(0\)。对于一个数 \(x\)，它能满足的位就是它取反后为 \(1\) 的地方。于是所有选出来的数取反后按位与起来就是全集。可以写出这样的暴力:
点击查看代码
for(int i=1;i<=n;++i){
for(int j=0;j<=all;++j){
f[j&a[i]]+=f[j];//这里的a[i]是取反后的
}
}//答案就是f[all]
但是我们不会 FWT，只能换个角度，正难则反，求不满足的方案数然后容斥。
考虑 \(f[S]\) 表示 \(S\) 内的位都不满足，其他位随便的方案数，显然只有 \(S\) 的补集的子集是可以选的，设补集的子集中满足的 \(a_i\) 个数为 \(cnt\)，则它的贡献就是 \(2^{cnt}\times\) 容斥系数。是不是又变成 SOSdp 的方法了？
点击查看代码
const int N=1e6+10,all=(1<<20)-1,mod=1e9+7;
int n,a[N];
int f[all+10],pw[N];
inline int count(int x){
int res=0;
while(x)++res,x-=x&-x;
return res;
}
int main(){
read(n);pw[0]=1;
for(int i=1;i<=n;++i){
read(a[i]);
pw[i]=2ll*pw[i-1]%mod;
a[i]=all&(~a[i]);++f[a[i]];//求和转变为求补集的子集的方案数
}
for(int i=0;i<20;++i)for(int S=0;S<=all;++S){
if(S&(1<<i))f[S]=(f[S]+f[S^(1<<i)])%mod;
}
int ans=0;
for(int i=0;i<=all;++i){
ans=((1ll*ans+1ll*(count(i)&1?-1:1)*pw[f[i]])%mod+mod)%mod;
}
printf("%d\n",ans);
return 0;
}
