10/6 牛客 2022 tg 第一场

难度？？？

A

细节巨多卡爆常数的二分答案，pass

B

二进制贡献考虑枚举位数，对于一个点，只有他自己和直接儿子可以有贡献， 统计第 \(i\) 位上 \(1\) 的个数 \(cnt\)，只有为奇数时有贡献 \(2^i\)，这样的方案数为 \(C_{cnt}^1+C_{cnt}^3+C_{cnt}^5+...\)=\(2^{cnt-1}\)。同时还要考虑其他不相关结点的移动，以及该点上只有一个点（无贡献）的情况，细节一堆。

C

考虑贪心构造，显然我们尽量让 \(AB\) 多次交换，把剩下的 \(A、B\) 尽量连续放在一起，

枚举 \(AB\) 交换了多少次，形如 BBB...BA BBB...BA

考虑填上剩下的 \(A\)：一个放在开头可以多 \(1\) 权值，剩下的在串里的每个 \(A\) 后面接上 \(a\) 个可获得 \(1\) 的权值。

考虑填上剩下的 \(B\)：一个放在末尾可以多 \(1\) 权值，剩下的填充进串里每凑足 \(b+1\) 个 \(B\) 可获得 \(1\) 的权值。

D

《容易看出》这是一个分段函数，形如

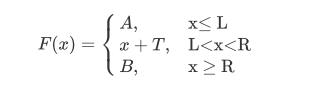
我们的目标是维护这个分段函数的两个断点 \(L\) 和 \(R\)。

（转载）

于是可以用线段树维护断点。

先考虑单个操作，\(f_{op}(x)\) 表示操作 \(op\) 的分段函数，有

\[f_1(x)=x+val,\ \ \ x\in(-\infty,+\infty)\\f_2(x)=\begin{cases}x,&x\in(-\infty,val)\\val,&x\in[val,+\infty)\end{cases}\\f_3(x)=\begin{cases}x,&x\in(val,+\infty)\\val,&x\in(-\infty,val]\end{cases} \]

再考虑如何合并，

若 \(f_1\) 后面跟着 \(f_2\)（避免歧义，将 \(f_1\) 中的 \(val\) 表示成 \(val'\)），则

\[f_2(f_1(x))=f_2(x+val')=\begin{cases}x+val',&x+val'\in(-\infty,val)\\val,&x+val'\in[val,+\infty)\end{cases} \]

即

\[f_2(f_1(x))=\begin{cases}x,&x\in(-\infty,val-val')\\val,&x\in[val-val',+\infty)\end{cases} \]

这里根据加上的值，断点位置会改变。跟着 \(f_3\) 同理。

若 \(f_2\) 后面跟着 \(f_1\)，则

\[f_1(f_2(x))=\begin{cases}x+val',&x\in(-\infty,val)\\val+val',&x\in[val,+\infty)\end{cases} \]

即直接加 \(val'\) 就行了，\(f_3\) 同理。

若 \(f_2\) 后面跟着 \(f_3\)（将 \(f_3\) 中的 \(val\) 表示成 \(val'\)），则

\[f_3(f_2(x))=\max(\min(x,val),val')=\begin{cases}x,& val'\le x\le val,\\val,& val'\le val\le x\\val',&x\le val'\end{cases} \]

事实上所谓的 \(\min\) 和 \(\max\)，它们的区别只是对初始值限制的范围不同，可以看作同一类型的函数。

综合以上，需要记录的有：断点 \(L\) 和 \(R\)，需要加的数 \(sum\)，可以写出以下维护代码：

#define ls p<<1
#define rs p<<1|1
struct node{ll sum,L,R;}tre[N<<2];

void pushup(int p){//左边合并到右边就是把左边的范围丢到右边限制一下
    tre[p].L=max(min(tre[ls].L,tre[rs].R-tre[ls].sum),tre[rs].L-tre[ls].sum);
    tre[p].R=max(min(tre[ls].R,tre[rs].R-tre[ls].sum),tre[rs].L-tre[ls].sum);
    tre[p].sum=tre[ls].sum+tre[rs].sum;
}

void modify(int p,int l,int r,int pos,int op,ll val){
    if(l==r){//限制范围
        if(op==1)tre[p]=(node){val,-inf,inf};
        if(op==2)tre[p]=(node){0,-inf,val};
        if(op==3)tre[p]=(node){0,val,inf};
        return;
    }
    int mid=l+r>>1;
    if(pos<=mid)modify(ls,l,mid,pos,op,val);
    else modify(rs,mid+1,r,pos,op,val);
    pushup(p);
}