做过的题
菜就多练
主要记录的是 dp 题(因为大部分都不会),还有一些思维题,还有一些 tricks,还有一些模板类的题。
CF533B Work Group
简要题意:
给定一棵树,要求选定一些点加入点集,使得这些点的权值和最大,且对于点集中的任意一个点,其子树中恰有奇数个点(可能包括它本身)被选中。
思路:
显然首先考虑树形 dp,设 \(f[u][0/1]\) 表示以 \(u\) 为根选出偶数/奇数个点的权值最大和,考虑到
可以这样转移:
就 OK 了。
点击查看代码
//main code
void dp(int u){
f[u][0]=0,f[u][1]=-1145141919810;
for(int v:e[u]){
dp(v);
ll qwq1=f[u][0],qwq2=f[u][1];
f[u][0]=max(qwq1+f[v][0],qwq2+f[v][1]);
f[u][1]=max(qwq2+f[v][0],qwq1+f[v][1]);
}f[u][1]=max(f[u][1],f[u][0]+a[u]);
}
signed main(){
cin>>n;
for(int i=1;i<=n;++i){
cin>>p[i]>>a[i];
if(~p[i])e[p[i]].push_back(i);
}
dp(1);
printf("%lld\n",max(f[1][0],f[1][1]));
return 0;
}
CF351B Jeff and Furik
简要题意:
给你一个长为 \(n\) 的排列 \(p\),接下来轮流进行两种操作:
-
任选两个相邻元素交换。
-
等概率地做以下子操作之一:
1). 对于所有 \(p[i]<p[i+1]\),随机取一对 \(p[i]\) 与 \(p[i+1]\) 交换。
2). 对于所有 \(p[i]>p[i+1]\),随机取一对 \(p[i]\) 与 \(p[i+1]\) 交换。
若操作完整个排列升序,结束。问在操作一最优的情况下,总操作数的期望值为多少。
思路:
对于相邻元素交换求排列升序,不难想到逆序对。
对于操作一,显然每次减少一个逆序对。
对于操作二,有 \(0.5\) 的概率增加或减少一个逆序对。
综上,则轮流一次,有 \(0.5\) 的概率减少 \(2\) 个逆序对或保持不变。
设 \(f[i]\) 表示逆序对数剩余 \(i\) 时的期望操作数,则有
可是不对劲,转移出现了自环,这时可以引入一个 trick :
将 \(f[i]\) 用 \(f[i+2]\) 表示,即类似解方程,有
于是答案就可以 \(O(1)\) 了。(注意逆序对数为奇数的情况)
点击查看代码
//main code
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i){
scanf("%d",&p[i]);
for(int j=1;j<i;++j)tot+=(p[j]>p[i]);//偷懒
}
printf("%.6lf\n",1.0*(tot*2-(tot&1)));
return 0;
}
CF1092F Tree with Maximum Cost
简要题意:
给你一棵树,树带点权 \(a[i]\),求一点 \(u\) 使
最大,求最大值。
思路:
对于“给你一棵树,求一点 \(u\)”一般先想换根 dp。
考虑 \(f[u]\) 表示以 \(u\) 为根的答案,\(sum[u]\) 表示子树权值和,现在转移到子结点 \(v\),对于 \(v\) 子树上的结点深度都 \(-1\) ,其余深度 \(+1\),则转移方程为
点击查看代码
//main code
void dfs1(int u,int fa){
dep[u]=dep[fa]+1;sum[u]=a[u];
for(int v:e[u]){
if(v==fa)continue;
dfs1(v,u);
sum[u]+=sum[v];
}
}
void dfs2(int u,int fa){
for(int v:e[u]){
if(v==fa)continue;
f[v]=f[u]+sum[u]-sum[v]*2;
sum[v]=sum[u];
dfs2(v,u);
}
}
# [P4630 [APIO2018] 铁人两项](https://www.luogu.com.cn/problem/P4630 "P4630 [APIO2018] 铁人两项")
int main(){
cin>>n;
for(int i=1;i<=n;++i)cin>>a[i];
for(int i=1;i<n;++i){
int x,y;cin>>x>>y;
e[x].push_back(y),e[y].push_back(x);
}
dep[0]=-1,dfs1(1,0);
for(int i=1;i<=n;++i)f[1]+=dep[i]*a[i];
dfs2(1,0);
ll ans=-1;
for(int i=1;i<=n;++i)ans=max(ans,f[i]);
printf("%lld\n",ans);
return 0;
}
CF734E Anton and Tree
简要题意:
给一棵 \(n(n<=200000)\) 个节点的树,每个点为黑色或白色,一次操作可以使一个相同颜色的连通块变成另一种颜色,求使整棵树变成一种颜色的最少操作数。
思路:
水紫。
显然先考虑把同一连通块的点缩成一个点,得到的新树一定是黑白相间的。再来考虑如何染色最优,显然一次性能改变的点越多越好,考虑一直在一个点反复染色,扩散到其他点,则操作数就是到离他最远的点的距离。贪心地想,最优即是直径的中点。
于是考虑在同色的相邻点连长为 \(0\) 的边,异色的相邻点连长为 \(1\) 的边,求直径即可。
点击查看代码
// main code
void dfs(int u,int fa){
for(int i=h[u];i;i=ne[i]){
int v=e[i];
if(v==fa)continue;
dfs(v,u);
res=max(res,f[u]+f[v]+w[i]);
f[u]=max(f[u],f[v]+w[i]);
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i)scanf("%d",&p[i]);
for(int i=1;i<n;++i){
int a,b;scanf("%d%d",&a,&b);
if(p[a]==p[b])add(a,b,0),add(b,a,0);
else add(a,b,1),add(b,a,1);
}
dfs(1,0);
printf("%d\n",res+1>>1);
return 0;
}
P5322 [BJOI2019] 排兵布阵
简要题意:

(不会概括)
思路:
考虑到每场对决的方案必须相同,派遣士兵的总数不能超过 \(m\) ,容易想到这是个背包。设 \(f[i][j]\) 表示争夺前 \(i\) 个城堡,派出 \(j\) 个士兵的最大总分,可以枚举打败了多少对手,设 \(a[i][j]\) 表示第 \(i\) 座城堡里对手士兵数的第 \(j\) 小,于是贪心地,只用派 \(2\times a[i][j]+1\) 人即可。
点击查看代码
// main code
int main(){
cin>>s>>n>>m;
for(int i=1;i<=s;++i)for(int j=1;j<=n;++j)cin>>a[j][i];
for(int i=1;i<=n;++i)sort(a[i]+1,a[i]+s+1);
for(int i=1;i<=n;++i){
for(int j=m;~j;--j){
for(int k=1;k<=s;++k){
if(j>a[i][k]*2){
f[j]=max(f[j],f[j-a[i][k]*2-1]+k*i);
}
}
}
}
for(int i=0;i<=m;++i)ans=max(ans,f[i]);
cout<<ans<<"\n";
return 0;
}
P1453 城市环路
简要题意:
给你一棵基环树,结点有点权,要求从中选出一些点,满足相邻两点不能同时选,求最大权值和。
思路:
显然如果只是一棵树,那么就变成了 没有上司的舞会。考虑基环树上怎么做。
对于基环树常用的解法就是断环,本题对路径没有强制要求,则任选环上相邻两点(假设为 \(s\) 和 \(t\)),断掉他们的边,再分别以他们为根做 dp,设 \(f[i][0/1]\) 表示以 \(i\) 为根的答案且 \(i\) 不选/选,则答案为 \(\max \{f[s][0],f[t][0]\}\)。(\(0\) 是因为保证两边不会同时选)。
点击查看代码
// main code
void dfs(int u,int ff){
f[u][0]=0,f[u][1]=p[u];
for(int v:e[u]){
if(v==ff||(s==u&&t==v)||(s==v&&t==u))continue;
dfs(v,u);
f[u][0]=f[u][0]+max(f[v][0],f[v][1]);
f[u][1]+=f[v][0];
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;++i)scanf("%d",&p[i]),fa[i]=i;
for(int i=1;i<=n;++i){
int x,y;scanf("%d%d",&x,&y);++x,++y;
e[x].push_back(y);e[y].push_back(x);
int u=found(x),v=found(y);
if(u==v){
s=x,t=y;
}else fa[v]=u;
}
scanf("%lf",&k);
int res=0;
memset(f,0,sizeof f);
dfs(s,t);res=f[s][0];
memset(f,0,sizeof f);
dfs(t,s);res=max(res,f[t][0]);
printf("%.1lf\n",1.0*res*k);
return 0;
}
双倍经验 P2607 [ZJOI2008] 骑士,但是基环森林
P3177 [HAOI2015] 树上染色
简要题意:
有一棵点数为 \(n\) 的树,树边有边权。给你一个在 \(0 \sim n\) 之内的正整数 \(k\) ,你要在这棵树中选择 \(k\) 个点,将其染成黑色,并将其他 的 \(n-k\) 个点染成白色。将所有点染色后,你会获得黑点两两之间的距离加上白点两两之间的距离的和的受益。问受益最大值是多少。
思路:
一眼树型 dp,设 \(f[u][k]\) 表示以结点 \(u\) 为根选 \(k\) 个黑点,类似树上背包的转移,考虑如何计算答案。
如果硬算点与点之间的贡献的话会很复杂,不如换个角度,考虑当前边对答案的贡献。
设当前的边是 \(u\to v\),边权为 \(W\),即用 \(v\) 更新 \(u\),枚举 \(v\) 中取了多少黑点,设为 \(j\),则 \(v\) 中有 \(size[v]-j\) 个白点。当前边的贡献即为 \(W\times\) 经过当前边的黑/白点对之间的数量,即 \(W\times[j\times (k-j)\ +\ (size[v]-j)\times(n-k-size[v]+j) ]\)。
点击查看代码
// main code
void dfs(int u,int fa){
size[u]=1;f[u][0]=f[u][1]=0;
for(int i=h[u];i;i=ne[i]){
int v=e[i];
if(v==fa)continue;
dfs(v,u);
size[u]+=size[v];
}
for(int i=h[u];i;i=ne[i]){
int v=e[i];
if(v==fa)continue;
for(int j=min(k,size[u]);j>=0;--j){
for(int s=0;s<=min(j,size[v]);++s){
if(f[u][j-s]==-1)continue;
ll qwq=1ll*(k-s)*s+1ll*(n-k-size[v]+s)*(size[v]-s);
f[u][j]=max(f[u][j],f[u][j-s]+f[v][s]+w[i]*qwq);
}
}
}
}
int main(){
cin>>n>>k;
for(int i=1;i<n;++i){
int a,b,c;cin>>a>>b>>c;
add(a,b,c),add(b,a,c);
}
memset(f,-1,sizeof f);
dfs(1,0);
cout<<f[1][k]<<"\n";
return 0;
}
P4630 [APIO2018] 铁人两项
简要题意:
给你 \(n\) 点 \(m\) 边的无向图,求有多少三元组 \((s,c,f)\) 满足,一条路径从 \(s\) 出发,经过 \(c\) 到达 \(f\)。
思路:
无向图上路径问题且与连通性相关思考广义圆方树,
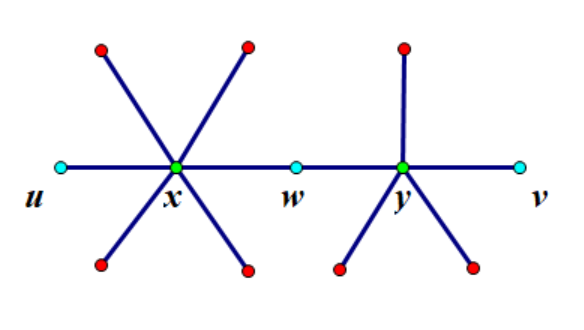
其中绿点表示方点,\((u,v)\) 之间于原图的简单路径条数相当于求其在圆方树路径上方点代表的点双大小之和,但显然 \(u\)、\(v\) 以及它们之间的割点(即路径上的所有圆点) \(w\) 都多算了一次,于是可以将方点权值设为点双大小,圆点权值设为 \(-1\),一个点对答案的贡献就是经过它的路径条数(显然)。
注意存在图不连通的情况。
点击查看代码
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
using namespace std;
const int N=2e5+10;
int n,m,cnt;
vector<int>e[N],g[N];
int stk[N],top,tot,dfn[N],low[N],tim;
int val[N],size[N];
void tarjan(int u){
dfn[u]=low[u]=++tim;stk[++top]=u;++tot;
for(int v:e[u]){
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]==dfn[u]){
g[++cnt].push_back(u),g[u].push_back(cnt);
val[u]=-1;val[cnt]=1;
for(int x=0;x!=v;){
x=stk[top--];
val[x]=-1;++val[cnt];
g[cnt].push_back(x),g[x].push_back(cnt);
}
}
}else low[u]=min(low[u],dfn[v]);
}
}
long long res=0;
void dfs(int u,int f){
size[u]=(u<=n);
long long qwq=0;
for(int v:g[u]){
if(v==f)continue;
dfs(v,u);
qwq+=1ll*size[u]*size[v];
size[u]+=size[v];
}qwq+=1ll*size[u]*(tot-size[u]);
res+=2ll*qwq*val[u];
}
int main(){
scanf("%d%d",&n,&m),cnt=n;
for(int i=1;i<=m;++i){
int x,y;scanf("%d%d",&x,&y);
e[x].push_back(y),e[y].push_back(x);
}
for(int i=1;i<=n;++i)if(!dfn[i])tarjan(i),dfs(i,0),top=tot=0;
printf("%lld\n",res);
return 0;
}
P4999 烦人的数学作业
简要题意:
给出一个区间 \(L\sim R\),求 \(L\) 到 \(R\) 区间内每个数的数字和,如 \(123\) 这个数的数字和为 \(1+2+3=6\)。共 \(T\) 次询问。(\(1 \leq L \leq R \leq 10^{18},1 \leq T \leq 20\))
思路:
算数位 dp 模板题。先确定前导零是否有影响,这道题里没有。数字和问题,考虑设 \(f[len][sum]\) 表示当前还有 \(len\) 位没填上数,已填的数的和为 \(sum\),即可。
点击查看代码
// main code:
ll dp(int len,int sum,bool lim){
if(!len)return sum;
if(!lim&&f[len][sum]!=-1)return f[len][sum];
ll res=0;
int t=lim?a[len]:9;
for(int i=0;i<=t;++i){
res=(res+dp(len-1,sum+i,lim&&i==t))%mod;
}
if(!lim)f[len][sum]=res;
return res;
}
ll work(ll x){
int tot=0;
while(x)a[++tot]=x%10,x/=10,g[tot]=(g[tot-1]*10+a[tot])%mod;
memset(f,-1,sizeof f);
return dp(tot,0,1);
}
int main(){
int t;ll l,r;
scanf("%d",&t);
while(t--){
scanf("%lld%lld",&l,&r);
printf("%lld\n",(work(r)-work(l-1)+mod)%mod);
}
return 0;
}
CF1197D Yet Another Subarray Problem
简要题意:
给 \(a_1, a_2, \cdots, a_n\) 和 \(m,k\),一个子区间 \([l,r]\) 的权值是 \(\sum\limits_{i=l}^r a_i-k\lceil \frac{r-l+1}{m}\rceil\) ,一个空区间的权值为 \(0\),请找到一个权值最大的区间,并输出其权值。(\(1≤n≤3×10^5,1≤m≤10\))
思路:
看到 \(\lceil \frac{r-l+1}{m}\rceil\) 很容易想到把序列分成大小为 \(m\) 的一个个块。考虑以 \(i\) 为区间左端点,则 \(a_{i+m},a_{i+2m},...\) (即对于 \(j\bmod m=i\) 的 $ a_j $)都作为块头减去 \(k\)。那么 \(i\) 只用取 \([0,m)\),枚举左端点 \(j=i+y\times m \,(y\in\mathbb{Z})\),预处理出右端点能取到哪就可以了,复杂度 O(nm)。
点击查看代码
//main code:
ll work(int x){
ll res=0;
for(int i=1;i<=n;++i){
sum[i]=sum[i-1]+a[i];
if(i%m==x)sum[i]-=k;//每块头减 k
}
maxn[n+1]=-1e18;
for(int i=n;i;--i)maxn[i]=max(maxn[i+1],sum[i]);//预处理右端点能取到哪
if(!x)x+=m;
for(int i=x;i<=n;i+=m){//枚举左端点
res=max(res,maxn[i]-sum[i-1]);
}
return res;
}
int main(){
scanf("%d%d%lld",&n,&m,&k);
for(int i=1;i<=n;++i)scanf("%lld",&a[i]);
for(int i=0;i<m;++i)ans=max(ans,work(i));
printf("%lld\n",ans);
return 0;
}
CF28D Don't fear, DravDe is kind
简要题意:

思路:
本题要求的是一个子序列,可以先考虑子序列中相邻元素的关系。我们发现:
也就是说 \(x\) 后面能跟上 \(y\) 必须得满足上面的条件,于是可以用 map 存能从哪里转移,做 dp 就可以了。
点击查看代码
//main code:
int main(){
scanf("%d",&n);
int v,c,l,r;
for(int i=1;i<=n;++i){
scanf("%d%d%d%d",&v,&c,&l,&r);
if(l&&mp[l].find(r+c)==mp[l].end())continue;
int x=mp[l][r+c];
f[i]=f[x]+v,pre[i]=x;
if(f[i]>f[mp[l+c][r]])mp[l+c][r]=i;
if(f[i]>f[id]&&!r)id=i;
}
while(id)ans[++tot]=id,id=pre[id];
printf("%d\n",tot);
for(int i=tot;i;--i)printf("%d ",ans[i]);
return 0;
}
P3287 [SCOI2014]方伯伯的玉米田
简要题意:
给定一长度为 \(n\) 的序列 \(a\),可进行最多 \(k\) 次区间 \(+1\) 操作。
求操作后的最长不下降子序列长度。(\(1<n<10000, 1< k\le 500, 1\le a_i \le 5000\))
思路:
码量不大,但是很有思维性的一道题。
首先考虑一次区间操作会对答案有什么影响:设对 \([l,r]\) 进行操作,
对于 \([1,l)\),不受影响,甚至有可能增加答案(因为 \([l,r]\) 原本比它矮的会变高)。
对于 \((r,n]\),有可能减少答案(原因同上)。
因此,从贪心的角度看,每次操作区间的右端点选 \(n\) 最优。
设 \(f[i][j]\) 表示拔高了 \([i,n]\) 共 \(j\) 次的答案,考虑能怎么转移到。
有 \(f[i][j]=max(f[x][y])+1\),其中 \(1\le x<i,0\le y\le j\),且 \(a[x]+y\le a[i]+j\)。
对 \(x\) 的限制可以由枚举顺序保证,其他两个可以用二维树状数组维护得到。
点击查看代码
#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
const int N=1e4+10,K=510;
int mn,n,k,a[N],ans=0;
int tre[N][N];
#define lb(x) (x&-x)
int query(int x,int y){
int res=0;
for(int i=x;i;i-=lb(i)){
for(int j=y;j;j-=lb(j)){
res=max(res,tre[i][j]);
}
}
return res;
}
void modify(int x,int y,int v){
for(int i=x;i<=k+1;i+=lb(i)){
for(int j=y;j<=mn+k;j+=lb(j)){
tre[i][j]=max(tre[i][j],v);
}
}
}
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;++i)scanf("%d",&a[i]),mn=max(mn,a[i]);
for(int i=1;i<=n;++i){
for(int j=k;~j;--j){
int qwq=query(j+1,a[i]+j)+1;
ans=max(ans,qwq);
modify(j+1,a[i]+j,qwq);
}
}
printf("%d\n",ans);
return 0;
}
CF1328E Tree Queries
简要题意:
给你一个以 \(1\) 为根的有根树.
每回询问 \(k\) 个节点 \({v_1, v_2 \cdots v_k}\)求出是否有一条以根节点为一端的链使得询问的每个节点到此链的距离均 \(\leq 1\).
只需输出可行性, 无需输出方案.
思路:
一眼虚树(bushi),可是我不会打。
观察一个点在链上或在链旁边有什么性质。这条链要么经过它自己,要么经过它父节点,要么经过它的任意一个儿子,观察到三种情况中这条链一定会经过它的父亲。于是问题就转化成,是否存在一条链,经过给定点的父亲。将父亲 \(dfs\) 序排一下,判断后一个是不是在前一个的子树上即可。
点击查看代码
void dfs(int u,int f){
dfn[u]=++tim;size[u]=1;fa[u]=f;
for(int v:e[u]){
if(v==f)continue;
dfs(v,u);
size[u]+=size[v];
}
}
int main(){
#ifdef LOCAL
freopen("std.in","r",stdin);
freopen("my.out","w",stdout);
#endif
read(n),read(m);
for(int i=1;i<n;++i){
int u,v;read(u),read(v);
e[u].push_back(v),e[v].push_back(u);
}dfs(1,1);
while(m--){
read(k);
for(int i=1;i<=k;++i)read(v[i]),v[i]=fa[v[i]];
sort(v+1,v+k+1,[=](int a,int b){return dfn[a]<dfn[b];});
bool flag=1;
for(int i=2;i<=k;++i){
if(dfn[v[i]]<dfn[v[i-1]]||dfn[v[i]]>dfn[v[i-1]]+size[v[i-1]]-1){flag=0;break;}
}
if(flag)printf("YES\n");
else printf("NO\n");
}
return 0;
}
CF1343E Weights Distributing
简要题意:
给出一个有 \(n\) 个点,\(m\) 条边的无向图和一个长为 \(m\) 的权值序列 \(w\)。
你可以随意安排边权(每条边权对应 \(w\) 中的一个数,不可以重复)。
求 \(a\) 到 \(b\) 的最短路与 \(b\) 到 \(c\) 的最短路的和的最小值。
思路:
安排边权首先考虑贪心。
假设只考虑 \(a\) 到 \(b\),有一个思路就是先将所有边权设为 \(i\) ,求出 \(a\) 到 \(b\) 最短路,根据其长度安排尽量小的边权。
现在加上 \(b\) 到 \(c\) 的路径,发现两条路径可能有重合的地方,设其为 \(x\) ,则路径总长度就是 \(dis(a,x)+2\times dis(b,x)+dis(c,x)\) ,这样又转化为了上面两个点的情况,枚举 \(x\) 即可。当然还有,从贪心角度来想,\(dis(b,x)\) 经过两次肯定要安排较小的边给它。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
template <typename T>
inline void read(T& r) {
r=0;bool w=0;
char ch=getchar();
while(ch<'0'||ch>'9') w=ch=='-'?1:0,ch=getchar();
while(ch>='0'&&ch<='9') r=(r<<3)+(r<<1)+(ch^48), ch=getchar();
r=w?-r:r;
}
const int N=2e5+10;
int n,m;
int dis[3][N],a,b,c;
long long w[N];
vector<int>e[N];
bool vis[N];
queue<int>q;
void init(int s,int op){
while(!q.empty())q.pop();
for(int i=1;i<=n;++i)dis[op][i]=1e9,vis[i]=0;
q.push(s),vis[s]=1;dis[op][s]=0;
while(!q.empty()){
int u=q.front();q.pop();
for(int v:e[u]){
if(vis[v])continue;
dis[op][v]=dis[op][u]+1;
vis[v]=1;q.push(v);
}
}
}
int main(){
#ifdef LOCAL
freopen("std.in","r",stdin);
freopen("my.out","w",stdout);
#endif
int t;read(t);
while(t--){
read(n),read(m);read(a),read(b),read(c);
for(int i=1;i<=m;++i)read(w[i]);
sort(w+1,w+m+1);
for(int i=2;i<=m;++i)w[i]+=w[i-1];
for(int i=1;i<=m;++i){
int u,v;read(u),read(v);
e[u].push_back(v);e[v].push_back(u);
}
init(a,0),init(b,1),init(c,2);
long long res=1e18;
for(int i=1;i<=n;++i){
int disa=dis[0][i],disb=dis[1][i],disc=dis[2][i];
if(disa+disb+disc>m)continue;
res=min(res,w[disa+disb+disc]+w[disb]);
}
printf("%lld\n",res);
for(int i=1;i<=n;++i)e[i].clear();
}
return 0;
}
P1297 [国家集训队]单选错位
简要题意:
有 \(n\) 道单选题,每道题有 \(a_i\) 个选项,但是填答案时错位,第 \(i\) 题答案填到 \(i+1\) 位置上(第 \(n\) 填到第 \(1\)),求做对题目的期望数。
思路:****
很有意思的期望题,根据期望的线性性,对每一道题单独求解
若 \(a_i=a_{i+1}\),则期望显然为 \(\frac{1}{a_i}=\frac{1}{a_{i+1}}\)。
若 \(a_i<a_{i+1}\),则第 \(i+1\) 题的正确答案在第 \(i\) 题的概率为 \(\frac{a_i}{a_{i+1}}\),期望为 \(\frac{a_i}{a_{i+1}}\times \frac{1}{a_i}=\frac{1}{a_{i+1}}\)
若 \(a_i>a_{i+1}\),则第 \(i+1\) 题的正确答案在第 \(i\) 题的概率为 \(\frac{a_{i+1}}{a_{i}}\),期望为 \(\frac{a_{i+1}}{a_{i}}\times \frac{1}{a_{i+1}}=\frac{1}{a_i}\)
综上,则总答案为 \(\sum\frac{1}{\max(a_i,a_i+1)}\)。
点击查看代码
int n,A,B,C,a[N];
db ans=0;
int main(){
scanf("%d%d%d%d%d", &n, &A, &B, &C, a + 1);
for (int i = 2; i <= n; i++)a[i] = ((long long) a[i - 1] * A + B) % 100000001;
for (int i = 1; i <= n; i++)a[i] = a[i] % C + 1;a[n+1]=a[1];
for(int i=1;i<=n;++i)ans+=1.0/(db)max(a[i],a[i+1]);
printf("%.3lf\n",ans);
return 0;
}
P6190 [NOI Online #1 入门组] 魔法
简要题意:
给你 \(n\) 点 \(m\) 边的有向图,每条边有边权 \(t_i\),求 \(1\) 到 \(n\) 的最小花费。走过一条边时,你可以使这条边的边权变为 \(-t_i\)(仅单次),最多可以做 \(k\) 次这个操作。(\(1\le n\le 100,1 \leq m \leq 2500,0 \leq k \leq 10^6\))
思路:
-
对于 \(k=0\),显然直接 floyd 就好了。
-
对于 \(k>0\),分层图?但注意到 \(k\) 十分的大,显然空间爆炸。
想想上面的 floyd,设 \(dis[p][i][j]\) 表示最多使用 \(p\) 次操作,从 \(i\) 到 \(j\) 的最小花费,显然有:
我们能想到啥?矩阵乘法!倍增!
先预处理出 \(k=1\) 时的情况:暴力枚举操作的边即可。
点击查看代码
const int N=150,M=3e3+10;
typedef long long ll;
int n,m,K;
int u[M],v[M];ll t[M];
ll dis[N][N];
struct matrix{ll m[N][N];}a;
matrix mul(matrix x,matrix y){
matrix res;
memset(res.m,0x3f,sizeof res.m);
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
res.m[i][j]=min(res.m[i][j],x.m[i][k]+y.m[k][j]);
}
}
}
return res;
}
matrix qpow(int b){
matrix res=a;
while(b){
if(b&1)res=mul(res,a);
b>>=1;
a=mul(a,a);
}
return res;
}
int main(){
read(n),read(m),read(K);
memset(a.m,0x3f,sizeof a.m);memset(dis,0x3f,sizeof dis);
for(int i=1;i<=n;++i)dis[i][i]=0;
for(int i=1;i<=m;++i){
read(u[i]),read(v[i]),read(t[i]);
dis[u[i]][v[i]]=min(dis[u[i]][v[i]],t[i]);
}
for(int k=1;k<=n;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}
}
}
if(K){
for(int k=1;k<=m;++k){
for(int i=1;i<=n;++i){
for(int j=1;j<=n;++j){
a.m[i][j]=min(a.m[i][j],min(dis[i][j],dis[i][u[k]]+dis[v[k]][j]-t[k]));
}
}
}
a=qpow(K-1);
printf("%lld\n",a.m[1][n]);
}else printf("%lld\n",dis[1][n]);
return 0;
}
太离谱了,你家入门组考紫题。
CF213C Relay Race
简要题意:
输入一个 \(n\times n\)的矩形,每个 \(a_{i,j}\) 是这个位置的价值。现在要从左上角走到右下角再返回,每个价值只被计算一次,求最大价值和。
思路:
P1004 [NOIP2000 提高组] 方格取数 和 P1006 [NOIP2008 提高组] 传纸条强化版。
走往返相当于走两遍。显然可以写 \(O(n^4)\) 的 dp,设 \(f_{i,j,k,l}\) 表示第一遍走到 \((i,j)\),第二遍走到 \((k,l)\) 的最大价值。时间上可以过,但是空间会炸。
注意到我们并不需要枚举那么多,两遍走的都是相同的路程,让它们同时走就行了,知道路程和当前的行(hang),可以推出当前的列,故设 \(f_{i,j,k}\) 表示当前走了 \(i\) 步,第一遍走到第 \(j\) 行,第二遍走到第 \(k\) 行的最大价值。于是就可以 \(O(n^3)\) 了。
于是对于重复的东西可以考虑通过相等部分做优化。
点击查看代码
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
#define getchar()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
template <typename T>
inline void read(T& r) {
r=0;bool w=0; char ch=getchar();
while(ch<'0'||ch>'9') w=ch=='-'?1:0,ch=getchar();
while(ch>='0'&&ch<='9') r=(r<<3)+(r<<1)+(ch^48), ch=getchar();
r=w?-r:r;
}
const int N=310;
int n,a[N][N],f[N<<1][N][N];//当前同时走了i步,第一个人在第j行,第二个人在第k行
int main(){
read(n);
for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)read(a[i][j]);
memset(f,-0x3f,sizeof f);
f[1][1][1]=a[1][1];
for(int i=2,tot=2*n-1;i<=tot;++i){
for(int j=1;j<=n;++j){
if(i-j+1<1||i-j+1>n)continue;
for(int k=1;k<=n;++k){
if(i-k+1<1||i-k+1>n)continue;
int h=i-j+1,l=i-k+1;
f[i][j][k]=max(max(f[i-1][j][k],f[i-1][j-1][k-1]),max(f[i-1][j][k-1],f[i-1][j-1][k]))+a[j][h]+a[k][l];
if(j==k)f[i][j][k]-=a[j][h];
}
}
}
printf("%d\n",f[2*n-1][n][n]);
return 0;
}
CF621E Wet Shark and Blocks
简要题意:
给你长为 \(n\) 的序列(\(0\le\) 每个数 \(\le 9\)),从中(可重复地)选 \(b\) 个数拼成一个 \(b\) 位数,求这个 \(b\) 位数模 \(x\) 余 \(k\) 的方案数。(\(2\le n\le 5\times10^4,1\le b\le 10^9,2\le x\le 100,0\le k<x\))
思路:
对于朴素 dp,显然设 \(f_{i,j}\) 表示当前选了 \(i\) 个数,余数为 \(j\) 的方案数。注意到 \(b\) 很大朴素是 \(O(nbx)\) 显然炸掉。
从数据规模角度考虑做法。做法肯定与 \(b\) 有关,\(b\le 10^9\),说明要 \(O(\log b)\);做法肯定与 \(x\) 有关,\(x\le100\),最多可以 \(O(x^3)\)。是不是很熟悉,矩阵快速幂啊。
流程:预处理转移矩阵,快速幂,输出答案,ok。
点击查看代码
const int N=5e4+10,M=110,mod=1e9+7;
int n,b,k,x,a[N];
struct Matrix{int m[M][M];}base;
Matrix mul(Matrix A,Matrix B){
Matrix res;
for(int i=0;i<x;++i)for(int j=0;j<x;++j)res.m[i][j]=0;
for(int s=0;s<x;++s){
for(int i=0;i<x;++i){
for(int j=0;j<x;++j){
res.m[i][j]=(res.m[i][j]+1ll*A.m[i][s]*B.m[s][j]%mod)%mod;
}
}
}
return res;
}
Matrix qpow(){
Matrix res;
for(int i=0;i<x;++i)res.m[i][i]=1;
while(b){
if(b&1)res=mul(res,base);
b>>=1;
base=mul(base,base);
}
return res;
}
int main(){
read(n),read(b),read(k),read(x);
for(int i=1;i<=n;++i){
read(a[i]);
for(int j=0;j<x;++j)++base.m[j][(j*10%x+a[i])%x];
}
printf("%d\n",qpow().m[0][k]);
return 0;
}
CF505E Mr. Kitayuta vs. Bamboos
简要题意:
自己看吧。
思路:
最小化最大值,显然二分答案,但怎么 \(check\) 呢?我们发现直接按顺序搞的话,很难判断该选哪个来操作。
这里引入了一个 trick,对于要按顺序操作求最终影响的问题,如果正向难做,不如考虑反向操作。
于是对于二分出的 \(mid\),先把所有的竹子高度设为 \(mid\),反向操作的话相当于每一轮选 \(k\) 个竹子“拔高” \(p\) 的高度,每轮结束后所有竹子高度减去 \(a_i\),如果这个 \(mid\) 可行,则每轮减去后所有竹子高度都 \(\ge0\),且所有操作结束后每个竹子的高度都 \(\ge h_i\)。
对于选出要拔高的竹子,我们可以贪心:若第 \(m\) 天结束后它的高度会 \(< 0\),则它肯定要拔高;按照危险程度(减少至 \(<0\) 的轮数)维护一个优先队列,每次取出前 \(k\) 个即可,若队列为空,则 \(mid\) 满足所有竹子的条件。
点击查看代码
const int N=1e5+10;
typedef pair<int,int> pr;
#define int long long
#define mp(x,y) make_pair(x,y)
int n,m,k,p,maxh=-1;
int f[N],h[N],a[N];//f[i]表示当前i的高度
bool check(int x){
priority_queue<pr>q;while(!q.empty())q.pop();
for(int i=1;i<=n;++i){
f[i]=x;
if(x-a[i]*m<h[i])q.push(mp(-x/a[i],i));
}
for(int i=1;i<=m&&!q.empty();++i){
for(int j=1;j<=k&&!q.empty();++j){
int id=q.top().second;q.pop();
if(f[id]-a[id]*i<0)return 0;
f[id]+=p;
if(f[id]-a[id]*m<h[id])q.push(mp(-f[id]/a[id],id));
}
}
return q.empty();
}
signed main(){
read(n),read(m),read(k),read(p);
for(int i=1;i<=n;++i)read(h[i]),read(a[i]),maxh=max(maxh,a[i]*m+h[i]);
int l=0,r=maxh,mid,ans=1e18;
while(l<=r){
mid=(l+r)>>1;
if(check(mid))ans=mid,r=mid-1;
else l=mid+1;
}
printf("%lld\n",ans);
return 0;
}
后面的题都只写思路不写题面了。
CF1706E Qpwoeirut and Vertices
求两点联通时间有个 trick,就是以每一条边连接的时间作为边权建立 kruskal 重构树,两点被连通的时间就是树上其 \(lca\) 的点权。设 \(ans_i=val_{lca(i,i+1)}\),即相邻两点联通时间。询问 \([l,r]\) 其实就是询问 \(\max^{r-1}_l ans_i\),线段树维护。
点击查看代码
const int N=4e5+10;
int n,m,q,fa[N],val[N],tot=0;
vector<int>e[N];
int son[N],size[N],dep[N],top[N];
int tre[N<<2],tmp[N];
inline int fnd(int x){return x!=fa[x]?fa[x]=fnd(fa[x]):x;}
void dfs1(int u,int f){
size[u]=1;dep[u]=dep[f]+1;
for(int v:e[u]){
dfs1(v,u);size[u]+=size[v];
if(size[v]>size[son[u]])son[u]=v;
}
}
void dfs2(int u,int t){
top[u]=t;if(son[u])dfs2(son[u],t);
for(int v:e[u])if(v!=son[u])dfs2(v,v);
}
int lca(int x,int y){
while(top[x]^top[y]){if(dep[top[x]]<dep[top[y]])swap(x,y);x=fa[top[x]];}
return dep[x]<dep[y]?x:y;
}
void build(int p,int l,int r){
if(l==r){tre[p]=tmp[l];return;}
int mid=(l+r)>>1;build(p<<1,l,mid),build(p<<1|1,mid+1,r);
tre[p]=max(tre[p<<1],tre[p<<1|1]);
}
int query(int p,int l,int r,int ql,int qr){
if(ql<=l&&r<=qr)return tre[p];
int mid=(l+r)>>1,res=0;
if(ql<=mid)res=max(res,query(p<<1,l,mid,ql,qr));
if(qr>mid)res=max(res,query(p<<1|1,mid+1,r,ql,qr));
return res;
}
void init(){
tot=n;
for(int i=1;i<=n*2;++i)fa[i]=i,e[i].clear();
memset(tre,0,sizeof tre),memset(tmp,0,sizeof tmp),memset(val,0,sizeof val);
memset(son,0,sizeof son);memset(dep,0,sizeof dep),memset(size,0,sizeof size),memset(top,0,sizeof top);
}
void solve(){
read(n),read(m),read(q);init();
for(int i=1;i<=m;++i){
int u,v;read(u),read(v);
int fu=fnd(u),fv=fnd(v);
if(fu!=fv){
val[++tot]=i;
e[tot].push_back(fu),e[tot].push_back(fv);
fa[fu]=fa[fv]=tot;
}
}
dfs1(tot,0),dfs2(tot,tot);
for(int i=1;i<n;++i)tmp[i]=val[lca(i,i+1)];
build(1,1,n-1);
while(q--){
int l,r;read(l),read(r);
printf("%d ",l==r?0:query(1,1,n-1,l,r-1));
}printf("\n");
}
int main(){
int t;read(t);
while(t--)solve();
return 0;
}
P6186 [NOI Online #1 提高组] 冒泡排序
设 \(a_i\) 表示 \(p_i\) 前面比它大的数的个数,显然整个排列的逆序对数 \(=\sum a_i\)。设 \(b_i\) 表示 \(a_j=i\) 的个数,则逆序对数又可写成 \(\sum_{i=0}^{n-1} i\times b_i\)。
考虑一轮冒泡对 \(a_i\) 有什么影响,通过模拟发现每过一轮,\(a_i\leftarrow\max(a_i-1,0)\)。
于是 \(k\) 轮操作后,剩下的逆序对数就是 \(\sum_{i=k}^{n-1}(i-k)\times b_i\),用线段树维护就行了。
点击查看代码
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int N=4e5+10;
#define int long long
#define lb x&-x
int n,m,p[N],tot[N];
int pre[N],tre[N];
int query(int x){
int res=0;
while(x)res+=tre[x],x-=lb;
return res;
}
void add(int x,int v){
while(x<=n)tre[x]+=v,x+=lb;
}
int sum1[N<<2],sum2[N<<2];
#define ls p<<1
#define rs p<<1|1
void build(int p,int l,int r){
if(l==r){
sum1[p]=tot[l]*l,sum2[p]=tot[l];
return;
}
int mid=(l+r)>>1;
build(ls,l,mid);build(rs,mid+1,r);
sum1[p]=sum1[ls]+sum1[rs],sum2[p]=sum2[ls]+sum2[rs];
}
void modify(int p,int l,int r,int pos,int k){
if(l==r){
sum2[p]+=k,sum1[p]=sum2[p]*l;
return;
}
int mid=(l+r)>>1;
if(pos<=mid)modify(ls,l,mid,pos,k);
else modify(rs,mid+1,r,pos,k);
sum1[p]=sum1[ls]+sum1[rs],sum2[p]=sum2[ls]+sum2[rs];
}
int query1(int p,int l,int r,int ql,int qr){
if(qr<ql)return 0;
if(ql<=l&&r<=qr)return sum1[p];
int mid=(l+r)>>1,res=0;
if(ql<=mid)res+=query1(ls,l,mid,ql,qr);
if(qr>mid)res+=query1(rs,mid+1,r,ql,qr);
return res;
}
int query2(int p,int l,int r,int ql,int qr){
if(qr<ql)return 0;
if(ql<=l&&r<=qr)return sum2[p];
int mid=(l+r)>>1,res=0;
if(ql<=mid)res+=query2(ls,l,mid,ql,qr);
if(qr>mid)res+=query2(rs,mid+1,r,ql,qr);
return res;
}
signed main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;++i){
scanf("%lld",p+i);
pre[p[i]]=i-query(p[i])-1;add(p[i],1);
tot[pre[p[i]]]++;
}build(1,0,n-1);
for(int i=1,t,c;i<=m;++i){
scanf("%lld%lld",&t,&c);
if(t==1){
if(p[c]<p[c+1])modify(1,0,n-1,pre[p[c]],-1),++pre[p[c]],modify(1,0,n-1,pre[p[c]],1);
else modify(1,0,n-1,pre[p[c+1]],-1),--pre[p[c+1]],modify(1,0,n-1,pre[p[c+1]],1);
swap(p[c],p[c+1]);
}else {
printf("%lld\n",query1(1,0,n-1,c,n-1)-c*query2(1,0,n-1,c,n-1));
}
}
return 0;
}
CF76A Gift
如果只求 \(s_i\) 或 \(g_i\) 的最大值那当然好求,直接搞 MST 就行,但是同时有了这两个条件,这个题就变得有意思了。
考虑先按照 \(g_i\) 排序,从小到大加入这条边(也就是先确定 \(\max g_i\)),然后维护关于 \(s_i\) 的 MST。发现 \(m\) 很大,我们不可能每次都花 \(O(m\log m)\) 的时间排序。注意到对于上一轮丢掉的边,在这一轮一定也不会用到,于是我们只用维护 \(O(n)\) 条边,每次用冒泡把新边加进去就不用 \(O(n\log n)\) 了,于是总时间复杂度 \(O(mn)\)。
点击查看代码
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
#define getchar()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
template <typename T>
inline void read(T& r) {
r=0;bool w=0; char ch=getchar();
while(ch<'0'||ch>'9') w=ch=='-'?1:0,ch=getchar();
while(ch>='0'&&ch<='9') r=(r<<3)+(r<<1)+(ch^48), ch=getchar();
r=w?-r:r;
}
const int N=300,M=5e4+10;
typedef long long ll;
int n,m,fa[N];ll G,S,ans=2e18;
struct node{int u,v;ll g,s;}e[M],tmp[M];int tot=0;
bool cmp(node a,node b){return a.g<b.g;}
int fnd(int x){return x!=fa[x]?fa[x]=fnd(fa[x]):x;}
void work(int x){
tmp[++tot]=e[x];
for(int i=tot-1;i&&tmp[i].s>tmp[i+1].s;--i)swap(tmp[i+1],tmp[i]);
for(int i=1;i<=n;++i)fa[i]=i;
int cnt=0;
for(int i=1;i<=tot;++i){
int u=fnd(tmp[i].u),v=fnd(tmp[i].v);
if(u!=v){tmp[++cnt]=tmp[i];fa[v]=u;}
if(cnt==n-1)break;
}
if(cnt==n-1)ans=min(ans,e[x].g*G+tmp[cnt].s*S);
tot=cnt;
}
int main(){
read(n),read(m);read(G),read(S);
for(int i=1;i<=m;++i){
int u,v;ll g,s;
read(u),read(v),read(g),read(s);
e[i]=(node){u,v,g,s};
}
sort(e+1,e+m+1,cmp);
for(int i=1;i<=m;++i)work(i);
printf("%lld\n",ans==2e18?-1:ans);
return 0;
}
CF893F Subtree Minimum Query
求子树内节点的最小权值很容易想到用 \(dfs\) 序,但是又多了“距离不超过 \(k\)”这个条件,可以转化成深度在 \([dep_x,dep_x+k]\) 的范围。
于是可以用主席树,以深度为时间轴,以 \(dfs\) 序为下标。查询就是查询时间轴为 \([dep_x,dep_x+k]\) 的主席树的区间 \([dfn_x,dfn_x+siz_x-1]\) 的最小值。
事实上 \(x\) 的子树中显然没有比 \(x\) 深度小的,直接查 \(dep_x+k\) 的区间就可以了。
点击查看代码
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
#include<queue>
using namespace std;
#define getchar()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
template <typename T>
inline void read(T& r) {
r=0;bool w=0; char ch=getchar();
while(ch<'0'||ch>'9') w=ch=='-'?1:0,ch=getchar();
while(ch>='0'&&ch<='9') r=(r<<3)+(r<<1)+(ch^48), ch=getchar();
r=w?-r:r;
}
const int N=1e5+10;
#define int long long
int n,m,s,a[N];
vector<int>e[N];
int dfn[N],tim=0,dep[N],siz[N];
int rt[N],tot=0,tre[N*50],ls[N*50],rs[N*50];
void dfs(int u,int fa){
dfn[u]=++tim,dep[u]=dep[fa]+1;siz[u]=1;
for(int v:e[u]){
if(v==fa)continue;
dfs(v,u);siz[u]+=siz[v];
}
}
void modify(int pre,int &cur,int l,int r,int pos,int v){
tre[cur=++tot]=tre[pre],ls[cur]=ls[pre],rs[cur]=rs[pre];
if(l==r){tre[cur]=v;return;}
int mid=l+r>>1;
if(pos<=mid)modify(ls[pre],ls[cur],l,mid,pos,v);
else modify(rs[pre],rs[cur],mid+1,r,pos,v);
tre[cur]=min(tre[ls[cur]],tre[rs[cur]]);
}
int query(int p,int l,int r,int ql,int qr){
if(!p)return 1e18;
if(ql<=l&&r<=qr)return tre[p];
int mid=(l+r)>>1,res=1e18;
if(ql<=mid)res=min(res,query(ls[p],l,mid,ql,qr));
if(qr>mid)res=min(res,query(rs[p],mid+1,r,ql,qr));
return res;
}
int tmp[N];
signed main(){
read(n),read(s);
for(int i=1;i<=n;++i)read(a[i]);
for(int i=1;i<n;++i){
int u,v;read(u),read(v);
e[u].push_back(v),e[v].push_back(u);
}dfs(s,0);tre[0]=2e9;
for(int i=1;i<=n;++i)tmp[i]=i;
sort(tmp+1,tmp+n+1,[](const int &a,const int &b){return dep[a]<dep[b];});
for(int i=1;i<=n;++i)modify(rt[dep[tmp[i-1]]],rt[dep[tmp[i]]],1,n,dfn[tmp[i]],a[tmp[i]]);
read(m);
for(int i=1,lstans=0,x,k;i<=m;++i){
read(x),read(k);x=(x+lstans)%n+1;k=(k+lstans)%n;
printf("%lld\n",lstans=query(rt[min(dep[x]+k,dep[tmp[n]])],1,n,dfn[x],dfn[x]+siz[x]-1));
}
return 0;
}
CF486D Valid Sets
\(n\) 很小,钦定某个点为根且为所在连通块最大值,设 \(f_u\) 表示已 \(u\) 为根的连通块个数,显然 \(f_u=\prod_{v\in son(u)}(1+f_v)\),但是注意相等元素之间不能重复贡献。
点击查看代码
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
#define getchar()(p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
char buf[1<<21],*p1=buf,*p2=buf;
template <typename T>
inline void read(T& r) {
r=0;bool w=0; char ch=getchar();
while(ch<'0'||ch>'9') w=ch=='-'?1:0,ch=getchar();
while(ch>='0'&&ch<='9') r=(r<<3)+(r<<1)+(ch^48), ch=getchar();
r=w?-r:r;
}
const int N=2100;
const long long mod=1e9+7;
int d,n,a[N];
vector<int>e[N];
long long f[N],ans;
bool cmp(int x,int y){return a[x]==a[y]?x<y:a[x]>a[y];}
void dfs(int rt,int u,int fa){
f[u]=1;
for(int v:e[u]){
if(v==fa)continue;
if(!cmp(rt,v)||a[rt]-a[v]>d)continue;
dfs(rt,v,u);
f[u]*=(1+f[v]);f[u]%=mod;
}
}
int main(){
read(d),read(n);
for(int i=1;i<=n;++i)read(a[i]);
for(int i=1,u,v;i<n;++i){
read(u),read(v);
e[u].push_back(v),e[v].push_back(u);
}
for(int i=1;i<=n;++i)dfs(i,i,0),ans=(ans+f[i])%mod;
printf("%lld\n",ans);
return 0;
}
CF1622D Shuffle
有思维价值的数数题,当然有一种思路就是双指针出每个极长区间,但是重复的情况比较复杂。
根据官方题解,我们从另外一个角度思考:我们不关注单个区间的变化,而是整体。
考虑枚举 \(i,j\) 表示发生变化的部分的左、右端点(即强制 \(i,j\) 变化,\([1,i)\) 和 \((j,n]\) 不变,然后 \(i,j\) 内部的 \(0,1\) 随便填),当然内部的 \(1\) 个数不能大于 \(k\),显然对于不同的 \(i,j\) 得到的最终序列都是互不相同的(因为 \(i,j\) 一定改变了)。设可以填的 \(0,1\) 个数为 \(cnt0\) 和 \(cnt1\),则对于单组 \(i,j\) 的答案就是 \(\dbinom{cnt0+cnt1}{cnt1}\)。
点击查看代码
#include<cstdio>
#include<iostream>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
const int N=5e3+10,mod=998244353;
int n,k,s[N],tot[N];
int C[N][N],ans=0;
int main(){
scanf("%d%d",&n,&k);
for(int i=1;i<=n;++i)scanf("%1d",&s[i]),tot[i]=tot[i-1]+s[i];
if(!tot[n]||tot[n]<k)return printf("1\n"),0;
memset(C,0,sizeof C);
C[0][0]=1;
for(int i=1;i<=n;++i){
C[i][0]=C[i][i]=1;
for(int j=1;j<i;++j){
C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
}
for(int i=1;i<=n;++i){
for(int j=i+1;j<=n;++j){//枚举 i,j 为发生变化的区间
int cnt=j-i-1,cnt1=tot[j]-tot[i-1];
if(cnt1>k)continue;
cnt1-=(!s[i])+(!s[j]);//强制 i,j 改变
ans=(ans+C[cnt][cnt1])%mod;
}
}
printf("%d\n",(ans+1)%mod);//啥都不变也是一种方案
return 0;
}
CF1717D Madoka and The Corruption Scheme
构造好题,既然我们能钦定一开始的排列顺序以及谁赢,不如我们把他直接确定下来,

红边表示钦定它赢,用 0 表示该边赢,1 表示该边输,则叶子节点都对应一个唯一的 01 串。全为 0 的那位就是最后的赢家。
对于赞助商单次改变结果的操作相当于将某个节点的 1 变成 0。对于一个人,赞助商想要他赢,它的编号不能有多于 \(k\) 个 1。
于是我们可以算出赞助商能钦定的赢家个数 \(cnt\),我们从小到大安排编号,那么最终的答案就是 \(cnt\) 啦。
\(cnt\) 怎么算?编号的二进制位有 \(n\) 位,其中 \(i\) 位是 \(1\) 的人就有 \(\dbinom{n}{i}\) 个,答案就是 \(\sum_{i=0}^{\min(n,k)}\dbinom{n}{i}\)。
点击查看代码
const int N=1e5+10,mod=1e9+7;
int n,k;
long long fac[N],ifac[N],ans=0;
long long qpow(long long a,int b){
long long res=1;
while(b){
if(b&1)res=res*a%mod;
b>>=1;a=a*a%mod;
}
return res;
}
long long C(int a,int b){
return fac[a]*ifac[b]%mod*ifac[a-b]%mod;
}
int main(){
read(n),read(k);fac[0]=1;
for(int i=1;i<=n;++i)fac[i]=1ll*i*fac[i-1]%mod;
ifac[n]=qpow(fac[n],mod-2);
for(int i=n-1;~i;--i)ifac[i]=1ll*(i+1)*ifac[i+1]%mod;
for(int i=0;i<=min(n,k);++i)ans=(ans+C(n,i))%mod;
printf("%lld\n",ans);
return 0;
}
P5283 [十二省联考 2019] 异或粽子
很 trick 的一道题,转换成前缀异或和,即求 \(k\) 对 \((i,j)\) 的 \(sum_i\oplus sum_{j-1}\) 的总和最大值。
一种暴力的想法显然就是 \(O(n^2)\) 枚举每一对然后选前 \(k\) 大。
求异或的最大值,首先就想到(可持久化) 01trie。
一个 trick:先求出以每个 \(i\) 为右端点,在 01trie 上找到对应左端点异或最大值,用个大根堆存着。对于每个取出来的位置 \(i\),假设它当前表示的是以 \(i\) 为右端点的 \(a\) 大值,我们再加入其 \(a+1\) 大值进去。这样减少了枚举,做 \(k\) 次就行了。求 kth 用 01trie 十分简单。
点击查看代码
const int N=5e5+10;
typedef long long ll;
int n,k;ll sum[N],ans=0;
int rt[N],cnt=0,son[N<<6][2],siz[N<<6];
void insert(int pre,int &cur,ll val,int bit=31){
siz[cur=++cnt]=siz[pre]+1;
son[cur][0]=son[pre][0],son[cur][1]=son[pre][1];
if(bit==-1)return;
int id=(val>>bit)&1;
insert(son[pre][id],son[cur][id],val,bit-1);
}
ll query(int cur,ll val,int k,int bit=31){
if(bit==-1||!siz[cur])return 0;
int id=(val>>bit)&1,t=id^1,s=siz[son[cur][t]];
if(k<=s)return (1ll<<bit)+query(son[cur][t],val,k,bit-1);
return query(son[cur][id],val,k-s,bit-1);
}
struct node{
ll val;int id,kth;
inline bool operator <(const node& a)const{
return val==a.val?id<a.id:val<a.val;
}
};
priority_queue<node>q;
int main(){
read(n),read(k);
insert(rt[0],rt[0],0);//一定要加!!!!!!
for(int i=1;i<=n;++i)read(sum[i]),insert(rt[i-1],rt[i],sum[i]^=sum[i-1]);
for(int i=1;i<=n;++i)q.push((node){query(rt[i-1],sum[i],1),i,1});//先加最大值
for(int i=1;i<=k;++i){
node tmp=q.top();q.pop();
ans+=tmp.val;
if(++tmp.kth<=tmp.id)q.push((node){query(rt[tmp.id-1],sum[tmp.id],tmp.kth),tmp.id,tmp.kth});
//加入 k+1 大值
}
printf("%lld\n",ans);
return 0;
}
一道类似的题:P2048 [NOI2010] 超级钢琴
P7913 [CSP-S 2021] 廊桥分配
嘻嘻,当年连签到题都不会打。(现在也不会捏)
注意到国内国际航班是相互独立的,不如分别预处理,把廊桥分配给航班,而不是按航班顺序把航班分配给廊桥。于是把航班丢到 \(set\) 里面,每次分配一个廊桥就贪心删 lower_bound。
点击查看代码
const int N=1e5+10;
typedef pair<int,int> pr;
int n,m1,m2,ans=0;
set<pr>s[2];
int cnt1[N],cnt2[N];
int calc(int op){
int tot=0,cur=0;
while(1){
auto it=s[op].lower_bound(make_pair(cur,cur));
if(it==s[op].end())break;
++tot;cur=(*it).second;
s[op].erase(it);
}
return tot;
}
int main(){
read(n),read(m1),read(m2);
for(int i=1,a,b;i<=m1;++i)read(a),read(b),s[0].insert({a,b});
for(int i=1,a,b;i<=m2;++i)read(a),read(b),s[1].insert({a,b});
for(int i=1;i<=n;++i)cnt1[i]=cnt1[i-1]+calc(0);
for(int i=1;i<=n;++i)cnt2[i]=cnt2[i-1]+calc(1);
for(int i=0;i<=n;++i)ans=max(ans,cnt1[i]+cnt2[n-i]);
printf("%d\n",ans);
return 0;
}
CF665E Beautiful Subarrays
一眼顶真,鉴定为前缀 01trie。
考虑查询 \(sum[i]\) 与 \(sum[0...i-1]\) 的异或和就行了。
设 \(k\) 当前位为 \(p\),\(sum[i]\) 当前位为 \(q\),
若 \(p=1\),则我们必须使当前位异或和为 \(1\),故跳到 \(q\oplus1\) 的地方。
若 \(p=0\),则异或和为 \(0\) 或 \(1\) 都可以,其中 \(1\) 是一定满足条件的,故加上贡献,跳到 \(q\oplus0=q\)。
最后记得加上叶子结点的贡献(此时总异或和 \(\ge k\))。
点击查看代码
const int N=1e6+10;
typedef long long ll;
int n,k,a[N];ll ans=0;
int tre[N*30][2],cnt[N*30],tot=1;
void insert(int x){
int pos=1;
for(int i=30;~i;--i){
int id=(x>>i)&1;
if(!tre[pos][id])tre[pos][id]=++tot;
pos=tre[pos][id],++cnt[pos];
}
}
ll query(int x){
ll res=0;int pos=1;
for(int i=30;~i;--i){
int id=(x>>i)&1,idk=(k>>i)&1;
if(idk)pos=tre[pos][id^1];
else res+=cnt[tre[pos][id^1]],pos=tre[pos][id];
}res+=cnt[pos];
return res;
}
int main(){
read(n),read(k);
for(int i=1;i<=n;++i){
read(a[i]);a[i]^=a[i-1];
insert(a[i-1]);ans+=query(a[i]);
}printf("%lld\n",ans);
return 0;
}
CF1251E2 Voting (Hard Version)
很好的贪心题与 STL 的运用。
考虑 \(m\) 从大到小枚举,因为 \(m\) 越大越难通过跟风来投票。
设比 \(m_i\) 小的个数为 \(p\),当前已被贿赂了 \(tot\) 个。若 \(p+tot\ge m_i\) 则可以不管这个 \(m_i\)。反之就得从里面贪心地选 \(m_i-p-tot\) 个来贿赂。
点击查看代码
#define pb push_back
const int N=2e5+10;
typedef long long ll;
int n;
multiset<ll>st;
vector<ll>a[N];
void solve(){
read(n);
for(int i=0;i<=n;++i)a[i].clear();
for(int i=1;i<=n;++i){
ll m,p;read(m),read(p);
a[m].pb(p);
}
st.clear();int left=n,tot=0;ll ans=0;
for(int i=n;~i;--i){
if(!a[i].size())continue;
for(ll v:a[i])st.insert(v);
left-=a[i].size();
int need=i-left-tot;
if(need<=0)continue;
while(need--){
++tot;
ans+=*st.begin();
st.erase(st.begin());
}
}
printf("%lld\n",ans);
}
CF103D Time to Raid Cowavans
注意到 \(k>\sqrt{n}\) 时 \(a_{t+pk}\) 个数不超过 \(\sqrt{n}\),\(k\le \sqrt{n}\) 时可以 \(O(n\sqrt{n})\) 预处理,显然根号分治。
但是直接预处理的话空间是会炸的,考虑将相同的 \(k\) 放在一起预处理,用个临时数组就好了。
点击查看代码
#define pb push_back
const int N=3e5+10,M=600;
typedef long long ll;
int n,m,t[N],k[N];
ll a[N],f[N+M],ans[N];
vector<int> q[600];
int main(){
read(n);
for(int i=1;i<=n;++i)read(a[i]);
read(m);
for(int i=1;i<=m;++i){
read(t[i]),read(k[i]);
if(k[i]>=500){
for(int j=t[i];j<=n;j+=k[i])ans[i]+=a[j];
}else q[k[i]].pb(i);
}
for(int i=1;i<500;++i){
if(!q[i].size())continue;
memset(f,0,sizeof f);
for(int j=n;j;--j)f[j]=a[j]+f[j+i];
for(int v:q[i])ans[v]=f[t[v]];
}
for(int i=1;i<=m;++i)printf("%lld\n",ans[i]);
return 0;
}
CF1194E Count The Rectangles
本来以为是什么神仙扫描线,结果是 bitset 的运用。
考虑 \(O(n^2)\) 预处理每条横线与竖线的相交情况,存在 bitset 里面。再 \(O(n^2)\) 枚举一对横线,查询同时与它们相交的竖线,总时间复杂度 \(O(\frac{n^3}{w})\)。
一个卡常小技巧:如果横线比竖线多,反过来,考虑枚举竖线求横线。
点击查看代码
const int N=5e3+10;
int n,tot1=0,tot2=0;
struct node{int a1,b1,a2,b2;}q1[N],q2[N];
bitset<N>f[N];
int main(){
read(n);
for(int i=1,a,b,c,d;i<=n;++i){
read(a),read(b),read(c),read(d);
if(a>c)swap(a,c);if(b>d)swap(b,d);
if(b==d)q1[++tot1]=(node){a,b,c,d};
else q2[++tot2]=(node){a,b,c,d};
}long long ans=0;
if(tot1<tot2){
for(int i=1;i<=tot1;++i){
for(int j=1;j<=tot2;++j){
if(q1[i].a1>q2[j].a1||q1[i].a2<q2[j].a1)continue;
if(q1[i].b1<q2[j].b1||q1[i].b1>q2[j].b2)continue;
f[i][j]=1;
}
}
for(int i=1;i<=tot1;++i){
for(int j=i+1;j<=tot1;++j){
long long qwq=(f[i]&f[j]).count();
ans+=qwq*(qwq-1)/2;
}
}
}else {
for(int i=1;i<=tot2;++i){
for(int j=1;j<=tot1;++j){
if(q2[i].a1<q1[j].a1||q2[i].a1>q1[j].a2)continue;
if(q2[i].b2<q1[j].b1||q2[i].b1>q1[j].b1)continue;
f[i][j]=1;
}
}
for(int i=1;i<=tot2;++i){
for(int j=i+1;j<=tot2;++j){
long long qwq=(f[i]&f[j]).count();
ans+=qwq*(qwq-1)/2;
}
}
}
printf("%lld\n",ans);
return 0;
}
CF768E Game of Stones
考虑以能取的最多次数作为 SG 函数值,然后就没了。注意判断的是后手是否胜利!!!
点击查看代码
int main(){
int n,sg=0;read(n);
for(int i=1,j,a;i<=n;++i){
read(a);
for(j=1;a>=j;++j)a-=j;
sg^=j-1;
}
!sg?printf("YES\n"):printf("NO\n");
return 0;
}
CF622E Ants in Leaves
由题意知,两个叶子节点深度相同,且它们的 lca 不是根,那么它们其中一个肯定要等一下。那么分别对根结点的每个子树 dfs,找到其每个子结点的深度,然后递推一下就行了。
点击查看代码
#define pb push_back
const int N=5e5+10;
int n;
vector<int>e[N];
int f[N],tot=0;
void dfs(int u,int fa,int dep){
for(int v:e[u]){
if(v==fa)continue;
dfs(v,u,dep+1);
}
if(e[u].size()==1)f[++tot]=dep;
}
int main(){
read(n);
for(int i=1,u,v;i<n;++i){
read(u),read(v);
e[u].pb(v),e[v].pb(u);
}int ans=0;
for(int v:e[1]){
tot=0;dfs(v,1,1);
sort(f+1,f+tot+1);
for(int i=1;i<=tot;++i)f[i]=max(f[i],f[i-1]+1);
ans=max(ans,f[tot]);
}printf("%d\n",ans);
return 0;
}
CF766E Mahmoud and a xor trip
套路题,显然考虑每一位对答案的贡献,就是经过它的使它贡献奇数次的路径数。设 \(f_{u,0/1}\) 表示经过 \(u\) 且第 \(i\) 位贡献偶/奇数次的路径数。
点击查看代码
#define pb push_back
const int N=1e5+10;
typedef long long ll;
int n,a[N];
vector<int>e[N];
ll f[N][2],ans=0;
void dfs(int u,int fa,int bit){
int cur=(a[u]>>bit)&1;
f[u][cur]=1,f[u][cur^1]=0;
for(int v:e[u]){
if(v==fa)continue;
dfs(v,u,bit);
ans+=(f[u][1]*f[v][0]+f[u][0]*f[v][1])*(1ll<<bit);
if(cur)f[u][1]+=f[v][0],f[u][0]+=f[v][1];
else f[u][0]+=f[v][0],f[u][1]+=f[v][1];
}
}
int main(){
read(n);
for(int i=1;i<=n;++i)read(a[i]),ans+=a[i];
for(int i=1,u,v;i<n;++i){
read(u),read(v);
e[u].pb(v),e[v].pb(u);
}for(int i=0;i<=20;++i)dfs(1,0,i);
printf("%lld\n",ans);
return 0;
}
CF1311F Moving Points
对于 \((i,j)\) 满足 \(x_i<x_j\),考虑可能的情况:
若 \(v_i>v_j\),则在以后某个时间一定会重合,所以 \(d(i,j)=0\)。
若 \(v_i\le v_j\),则它们的距离一定不变或越来越远,于是 \(d(i,j)=x_j-x_i\),即初始距离。
于是答案就是 \(\sum d(i,j) [x_i<x_j][v_i\le v_j]\),二维偏序。
点击查看代码
const int N=2e5+10;
typedef long long ll;
#define lb x&-x
int n,tmp[N],tot=0;
struct node{int x,v;}a[N];
ll ans=0,tre1[N],tre2[N];
void modify1(int x,ll v){while(x<=n)tre1[x]+=v,x+=lb;}
void modify2(int x,ll v){while(x<=n)tre2[x]+=v,x+=lb;}
ll query1(int x,ll res=0){while(x)res+=tre1[x],x-=lb;return res;}
ll query2(int x,ll res=0){while(x)res+=tre2[x],x-=lb;return res;}
int main(){
read(n);
for(int i=1;i<=n;++i)read(a[i].x),tmp[i]=a[i].x;
for(int i=1;i<=n;++i)read(a[i].v);
sort(a+1,a+n+1,[&](node a,node b){return a.v==b.v?a.x<b.x:a.v<b.v;});
sort(tmp+1,tmp+n+1);tot=unique(tmp+1,tmp+n+1)-tmp-1;
for(int i=1;i<=n;++i){
a[i].x=lower_bound(tmp+1,tmp+tot+1,a[i].x)-tmp;
ans+=query1(a[i].x)*tmp[a[i].x]-query2(a[i].x);
modify1(a[i].x,1ll),modify2(a[i].x,tmp[a[i].x]);
}
printf("%lld\n",ans);
return 0;
}
P7997 [WFOI - 01] 刷题 (problem)
注意到取同一个 \(a_i\) 两次等于没取,所以知 \(ans\le 2\times a_{max}-1\),直接连边跑奇偶最短路即可。
点击查看代码
#define pb push_back
const int N=1e5+10;
typedef long long ll;
typedef pair<int,int> pr;
int n,T,a[N];ll m;
vector<int>e[N<<1];
ll f[N][2];bool vis[N][2];
queue<pr>q;
void bfs(int s){
memset(f,0x3f,sizeof f);
q.push({s,0});vis[s][0]=1;f[s][0]=0;
while(!q.empty()){
int u=q.front().first,t=q.front().second;q.pop();
for(int v:e[u]){
if(vis[v][t^1])continue;
f[v][t^1]=f[u][t]+1;
vis[v][t^1]=1;q.push({v,t^1});
}
}
}
int main(){
read(n),read(T);
int maxn=-1;
for(int i=1;i<=n;++i)read(a[i]),maxn=max(maxn,a[i]);
for(int i=0;i<=2*maxn-1;++i)for(int j=1;j<=n;++j)e[i].pb(i>=a[j]?i-a[j]:i+a[j]);
bfs(0);
while(T--){
read(m);
for(int i=2*maxn-1;~i;--i){
if(f[i][m&1]<=m){printf("%d\n",i);break;}
}
}
return 0;
}
P4060 [Code+#1]可做题
看到异或想到按位贡献。
对于未知的地方,可以设成 \(0\)。对于已知的地方,考虑连续一段的贡献。
假设这一段是 \([l,r]\),则它们这一位由 \(0\) 还是 \(1\) 贡献取决于 \(a_{l-1}\) 填的是 \(0\) 还是 \(1\),贪心地选就好了。
点击查看代码
const int N=1e5+10;
typedef long long ll;
int n,m;ll ans=0;
struct node{int id,val;}a[N];
int main(){
read(n),read(m);
for(int i=1;i<=m;++i)read(a[i].id),read(a[i].val);
sort(a+1,a+m+1,[&](node a,node b){return a.id<b.id;});
for(int bit=0;bit<=30;++bit){
for(int i=1;i<=m;){
int j=i+1;
while(a[j].id==a[j-1].id+1)++j;
int res0=0,res1=1,cur0=0,cur1=1;
for(int k=i;k<j;++k){
int t=a[k].val>>bit&1;
cur0^=t,cur1^=t;
res0+=cur0,res1+=cur1;
}//res0:未知位填0的贡献;res1:未知位填1的贡献
if(a[i].id==1)ans+=(1ll*res0)<<bit;
else ans+=(1ll*min(res0,res1))<<bit;
i=j;
}
}
printf("%lld\n",ans);
return 0;
}
CF1517D Explorer Space
恰好走 \(k\) 步回到自身的最短路,显然是走过去再原路返回,维护走 \(\frac{k}{2}\) 步最近能走多远即可。\(k\) 为奇数时无解。
点击查看代码
const int N=510;
int n,m,k;
int a[N][N],b[N][N],f[N][N][30];
int main(){
read(n),read(m),read(k);
if(k&1){
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j)printf("-1 ");
printf("\n");
}return 0;
}
for(int i=1;i<=n;++i)for(int j=1;j<m;++j)read(a[i][j]);
for(int i=1;i<n;++i)for(int j=1;j<=m;++j)read(b[i][j]);
memset(f,0x3f,sizeof f);k>>=1;
for(int i=1;i<=n;++i)for(int j=1;j<=m;++j)f[i][j][0]=0;
for(int t=1;t<=k;++t){
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j){
int &res=f[i][j][t];
if(i>=2)res=min(res,f[i-1][j][t-1]+b[i-1][j]);
if(i<=n-1)res=min(res,f[i+1][j][t-1]+b[i][j]);
if(j>=2)res=min(res,f[i][j-1][t-1]+a[i][j-1]);
if(j<=m-1)res=min(res,f[i][j+1][t-1]+a[i][j]);
}
}
}
for(int i=1;i<=n;++i){
for(int j=1;j<=m;++j)printf("%d ",f[i][j][k]<<1);
printf("\n");
}
return 0;
}
AT Edu DP Contest U Grouping
数据范围显然状压,考虑预处理出每种可能的集合的得分,转移的时候考虑子集,即强制分组。
点击查看代码
const int N=20;
typedef long long ll;
int n;
ll a[N][N],f[1<<N];
int main(){
read(n);int lim=(1<<n)-1;
for(int i=0;i<n;++i)for(int j=0;j<n;++j)read(a[i][j]);
for(int i=0;i<=lim;++i){
for(int j=0;j<n;++j)if(i>>j&1){
for(int k=0;k<n;++k)if(i>>k&1){
f[i]+=a[j][k];
}
}
}
for(int i=0;i<=lim;++i)for(int j=i;j;j=i&(j-1))f[i]=max(f[i],f[j]+f[i^j]);
printf("%lld\n",f[lim]/2);
return 0;
}
AT Edu DP Contest V Subtree
换根 dp 是 trivial 的,问题就出在于 \(m\) 不一定是质数上,这意味着不能直接求逆元。于是只能按照朴素的方法即 \(f_u=\prod_{v\in to(u)}(f_v+1)\)。
考虑优化,可以求出其到达的所有结点(包括父节点)的前、后缀积。根从 \(u\) 换到 \(v\) 时,本来要用除法消去 \(v\) 的贡献,现在转为前后缀积乘一下即可。
点击查看代码
#define pb push_back
const int N=1e5+10;
typedef long long ll;
int n;ll m;
vector<int>e[N];
ll f[N],ans[N];
void dfs(int u,int fa){
f[u]=1;
for(int v:e[u])if(v!=fa){
dfs(v,u);f[u]=f[u]*(f[v]+1)%m;
}
}
void dfs2(int u,int fa){//关键部分
int sz=e[u].size();
vector<ll> pre(sz+1,1),suf(sz+1,1);
for(int i=0;i<sz;++i)pre[i+1]=pre[i]*(f[e[u][i]]+1)%m;
for(int i=sz-1;~i;--i)suf[i]=suf[i+1]*(f[e[u][i]]+1)%m;
ans[u]=pre[sz];
for(int i=0;i<sz;++i){
int v=e[u][i];
if(v==fa)continue;
f[u]=pre[i]*suf[i+1]%m;
dfs2(v,u);
}
}
int main(){
read(n);read(m);
for(int i=1,a,b;i<n;++i){
read(a),read(b);
e[a].pb(b),e[b].pb(a);
}dfs(1,0),dfs2(1,0);
for(int i=1;i<=n;++i)printf("%lld\n",ans[i]);
return 0;
}
P5994 [PA2014]Kuglarz
有点牛逼的转化题意的题。
如果我要确认所有位置的信息,即区间 \([i,i] (1\le i\le n)\),则至少需要 \(n\) 次询问。
如果我已经知道了 \([l,r1]\) 和 \([l,r2]\) (\(r1<r2\)),则 \([r1+1,r2]\) 的信息也能得出。这相当于连了 \((l,r1)\) 和 \((l,r2)\) 两条边,那么,\((r1+1,r2)\) 就不用连了。若所有点都联通,是不是所有点的信息都能知道了?
是不是有点像建 MST?但是还不够优雅,因为我们不可能将自己和自己连边,而且我们需要 \(n\) 条边,\((r1+1,r2)\) 里的 \(+1\) 也很难搞。
于是将查询 \([l,r]\) 的信息变成连 \((l-1,r)\) 这条边即可(也就是加了个 \(0\) 号点),那么,连 \((l-1,r1)\) 和 \((l-1,r2)\) 就不用连 \((r1,r2)\) 了。优雅,实在是太优雅了!
点击查看代码
const int N=2e3+10;
typedef long long ll;
int n,fa[N],tot;
struct node{int u,v;ll w;}e[N*N];
ll ans=0;
int fnd(int x){return x==fa[x]?x:fa[x]=fnd(fa[x]);}
int main(){
read(n);
for(int i=1;i<=n;++i){
fa[i]=i;
for(int j=i,a;j<=n;++j){
read(a);e[++tot]=(node){i-1,j,a};
}
}sort(e+1,e+tot+1,[&](node a,node b){return a.w<b.w;});
for(int i=1,cnt=0;i<=tot&&cnt<n;++i){
int u=fnd(e[i].u),v=fnd(e[i].v);ll w=e[i].w;
if(u!=v){
fa[v]=u;++cnt;
ans+=w;
}
}printf("%lld\n",ans);
return 0;
}
CF1681F Unique Occurrences
感觉之前某场膜你赛做过类似的题,就是树上路径数颜色。
考虑每一种颜色对答案的贡献:删去该颜色的所有边,贡献就是原先相连的连通块大小相乘。
如图,红边就是删去的边。

贡献就是原先红边相连的两个连通块大小乘积。

怎么算贡献?LCT?我不会打。考虑对于颜色分治,\(solve(l,r)\) 表示分治颜色在 \([l,r]\) 的边。
加上左半部分颜色的边,然后分治右半边,接着删掉左半边,加上右半边,然后分治左半边。如果 \(l=r\),则计算贡献。加边删边可以用可撤销并查集(有点像线段树分治,或许就是)。
点击查看代码
#define pb push_back
const int N=5e5+10;
typedef pair<int,int> pr;
#define fi first
#define se second
int n;long long ans=0;
vector<pr> e[N];
int fa[N],siz[N];
int fnd(int x){return x!=fa[x]?fnd(fa[x]):x;}
void work(int l,int r,vector<pr>& qwq){
for(int i=l;i<=r;++i)for(pr tmp:e[i]){
int u=fnd(tmp.fi),v=fnd(tmp.se);
if(u==v)continue;
if(siz[u]<siz[v])swap(u,v);
fa[v]=u,siz[u]+=siz[v];
qwq.pb({u,v});
}
}
void undo(vector<pr>& qwq){
for(pr tmp:qwq){
siz[tmp.fi]-=siz[tmp.se];
fa[tmp.se]=tmp.se;
}qwq.clear();
}
void solve(int l,int r){
if(l==r){
for(pr tmp:e[l]){
ans+=1ll*siz[fnd(tmp.fi)]*siz[fnd(tmp.se)];
}
return;
}
int mid=(l+r)>>1;vector<pr>qwq;
work(l,mid,qwq),solve(mid+1,r),reverse(qwq.begin(),qwq.end()),undo(qwq);
work(mid+1,r,qwq),solve(l,mid),reverse(qwq.begin(),qwq.end()),undo(qwq);
//为保正确,记得一定要reverse后再撤销
}
int main(){
read(n);
for(int i=1;i<=n;++i)fa[i]=i,siz[i]=1;
for(int i=1,u,v,w;i<n;++i){
read(u),read(v),read(w);
e[w].pb({u,v});
}solve(1,n);
printf("%lld\n",ans);
return 0;
}
AT Edu Contest X tower
显然 01 背包,但是转移的顺序对答案有影响。显然贪心地把能承重的放在下面,但是如何正确排序?
注意到对于一种枚举顺序,交换相邻两个的位置不影响其他的答案。设它们为 \(x,y\) 且 \(x\) 在 \(y\) 上面,则我们要让 \(y\) 承载完 \(x\) 后还能承载的比 \(x\) 多,即
移项得 \(s_x+w_x<s_y+w_y\)。我们枚举的顺序是从上到下。
点击查看代码
const int N=1e3+10,M=1e4+10;
typedef long long ll;
int n;
struct node{int w,s,v;}a[N];
ll f[M<<1];
int main(){
read(n);
for(int i=1;i<=n;++i)read(a[i].w),read(a[i].s),read(a[i].v);
sort(a+1,a+n+1,[&](node a,node b){return a.w+a.s<b.w+b.s;});
for(int i=1;i<=n;++i){
for(int j=a[i].s;~j;--j){
f[j+a[i].w]=max(f[j+a[i].w],f[j]+a[i].v);
}
}printf("%lld\n",*max_element(f,f+a[n].w+a[n].s+1));
return 0;
}
CF1638C Inversion Graph
若 \(i\) 向 \(j\) 有连边,则 \([i,j]\) 一定在一个连通块里面,因为不是比 \(p_j\) 大就是比 \(p_i\) 小。
那么,若 \([i,j]\) 是个极大连通块,则 \(j\) 后面的数一定都比 \(p_i\) 大。
既然如此,\([1,j]\) 一定组成了一个 \(j\) 的排列。
点击查看代码
void solve(){
read(n);int ans=0,maxn=-1;
for(int i=1;i<=n;++i){
if(maxn<i)++ans;
read(a);
maxn=max(a,maxn);
}printf("%d\n",ans);
}
CF1335F Robots on a Grid
数据保证在每个点开始都能无限走下去,且每个点都有唯一的一个方向,则构造出的图构成了一个内向基环树,每个点最终都会走到环里面。
要满足每个机器人都不相撞,则机器人个数最多就是环的大小,那么黑色结点个数呢?
对于环上的一个白点,我们可以将任意一个能走到它的黑点替换它上面的机器人,为什么这样是正确的?因为两个机器人如果要相遇,一定是在走到环之前的路上相遇的,它们最终也会走到环上的同一个点,我们只要选它们之中任意一个黑色的就行了。
现在的问题就是找环以及找满足条件的黑点,直接建基环树做有点麻烦。
考虑枚举起始点贡献环上的点,如何找到环上对应的点?显然,它走 \(n\times m\) 步走到的一定就是(至少走 \(n\times m\) 步进入环上),咋走?倍增。
点击查看代码
const int N=1e6+10;
int n,m;
int to[N][21];
bool col[N],black[N],white[N];
void solve(){
scanf("%d%d",&n,&m);n*=m;
char ch;
for(int i=1;i<=n;++i)scanf(" %c",&ch),col[i]=ch=='1';
for(int i=1;i<=n;++i){
scanf(" %c",&ch);
if(ch=='U')to[i][0]=i-m;
else if(ch=='D')to[i][0]=i+m;
else if(ch=='L')to[i][0]=i-1;
else to[i][0]=i+1;
}
for(int i=1;i<=20;++i)for(int j=1;j<=n;++j)to[j][i]=to[to[j][i-1]][i-1];
for(int i=1;i<=n;++i){
int pos=i;
for(int j=20;~j;--j)if(n>>j&1)pos=to[pos][j];
col[i]?white[pos]=1:black[pos]=1;
}
int ans1=0,ans2=0;
for(int i=1;i<=n;++i){
if(black[i])++ans1,++ans2;
else if(white[i])++ans1;
black[i]=white[i]=0;
}printf("%d %d\n",ans1,ans2);
}
CF1336A Linova and Kingdom
写 dp 写傻了,显然这题用 dp 难写啊。考虑贪心选点,肯定从深度最深的选啊,其他的怎么办?一个点被选到当且仅当其子树内的点都选了,因为其子树肯定比它优,选了它则其子树内的贡献都要减 1,那我们可以设一个点的权值为 \(dep_u-siz_u\),答案就是取前 \(k\) 大就行了啊。
点击查看代码
#define pb push_back
#define int long long
const int N=2e5+10;
int n,k,a[N],ans=0;
vector<int> e[N];
int dep[N],siz[N];
void dfs(int u,int fa){
dep[u]=dep[fa]+1;siz[u]=1;
for(int v:e[u]){
if(v==fa)continue;
dfs(v,u);siz[u]+=siz[v];
}a[u]=dep[u]-siz[u];
}
signed main(){
read(n),read(k);
for(int i=1,u,v;i<n;++i){
read(u),read(v);
e[u].pb(v),e[v].pb(u);
}dfs(1,0);
nth_element(a+1,a+k+1,a+n+1,[&](int a,int b){return a>b;});
for(int i=1;i<=k;++i)ans+=a[i];
printf("%lld\n",ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号