【DP】决策单调性小记
何谓决策单调性?
指的就是在最优化 dp 中,状态的最优转移点单调不减的性质。
这使得我们在做 dp 的时候可以减少冗余计算以达到优化的效果。这类优化方法常用于分段问题。
0x01:四边形不等式
设 \(f[i]\) 表示将前 \(i\) 个位置分段的最小代价,\(w(j,i)\) 表示从 \(j\) 转移到 \(i\) 的代价。
若对于 \(a\le b\le c\le d\),满足
我们就说 \(w\) 满足四边形不等式。
\(\bullet\) 结论:若 \(w\) 满足四边形不等式,则该 dp 问题具有决策单调性。
采取反证法:设 \(f[i]\) 的最优决策点为 \(p[i]\),且代价函数 \(w\) 满足四边形不等式。假设对于 \(j< i\),有 \(p[i]\le p[j]\),则根据最优性质,有
又根据四边形不等式,因为 \(p[i]\le p[j]\le j\le i\),所以有
\((1)(2)\)两式相加,两边消去相同项,得到
也就是说,从 \(p[i]\) 转移到 \(j\),比从 \(p[j]\) 转移更优,与我们的假设相悖,故结论得证。
不过在实战中,四边形不等式一般较难证明,暴力输出各决策点的方式确定决策单调性是最方便的。
0x02:在 \(\boxed{\mathrm{2D/1D}}\) dp 中的运用
这一类型的 dp 有分 \(k\) 段问题和区间 dp,朴素的 dp 一般是 \(O(n^3)\) 的,如果 \(w\) 满足四边形不等式,则我们可以用决策单调性来优化到 \(O(n^2)\) 的复杂度。
\(\bullet\) 结论:设 \(p_{i,j}\) 表示 \(f_{i,j}\) 的最优决策点,若 \(w\) 满足四边形不等式,则有 \(p_{i,j-1}\le p_{i,j}\le p_{i+1,j}\)。证明略。
例题 1:
\(\circ\) luoguP4767 [IOI2000]邮局
题目大意:一条数轴上有 \(n\) 个村庄,第 \(i\) 个村庄的位置为 \(a_i\),你需要放置 \(m\) 个邮局,使得每个村庄到最近的邮局的距离和最小(\(1\le m\le 300\),\(m\le n\le 3000\),\(a_i\in [1,10000]\))。也就是说这个问题是一个分 \(k\) 段问题。
设 \(f_{i,j}\) 表示在前 \(i\) 个村庄中放 \(j\) 个邮局的最小距离和,\(w(i,j)\) 表示在编号(从小到大)为 \([i,j]\) 的村庄中放一个邮局的代价(显然放在中位数处最优)。有状态转移方程
先做一遍 \(O(nm^2)\) 的暴力,求出每个状态的最优决策点并输出,我们可以发现满足 \(p_{i,j-1}\le p_{i,j}\le p_{i+1,j}\)
于是我们枚举 \(f_{i,j}\) 的决策点时候,可以枚举 \(k:p_{i,j-1}\le k\le p_{i+1,j}\),复杂度降为 \(O(nm)\)。
由于需要用到 \(f_{i+1,j}\) 的决策点,我们需要倒序枚举 \(i\)。
例题 2:
\(\circ\) CF833B The Bakery
题目大意:将一个长度为 \(n\) 的序列分为 \(k\) 段,使得总价值最大。一段区间的价值表示为区间内不同数字的个数。(\(n\leq 35000,k\leq 50\))
还是熟悉的分 \(k\) 段问题,\(f_{i,j}\) 表示前 \(i\) 个位置分 \(j\) 段,状态转移方程直接出来
我们发现 \(w\) 是个数颜色问题,具有决策单调性(大概就是区间越长越亏),但并不能快速的得出。
注意到每次转移都是由第 \(j-1\) 层转移到第 \(j\) 层,也就是说同层之间不会转移,我们可以用上一层区间 \([0,n-1]\) 的结果去转移当前区间 \([1,n]\) 的结果,连续做 \(k\) 次,不就得到答案了吗?
考虑一种分治做法,记 \(solve(ql,qr,L,R)\) 表示从上一次分治的 \([L,R]\) 转移到 \([ql,qr]\)。对于 \(mid=\lfloor\frac{ql+qr}{2}\rfloor\),我们可以先求出它的最优决策点 \(p\),由决策单调性可知,\([ql,mid)\) 一定由 \([L,p]\) 转移而来,\((mid,qr]\) 一定由 \([p,R]\) 转移而来。
对于 \(w\) 的计算,由数颜色我们想到类似莫队的方法转移,维护当前左右端点 \(tl,tr\),随着分治移动,时间复杂度 \(O(n\log n)\),\(k\) 次分治就是 \(O(nk\log n)\)。
也就是说,当 \(w\) 的贡献难算时,可采用分治的方法。
但注意,分治方法仅适用于一轮决策用上一轮结果转移的情况,如果同层转移则不可用。
习题:
\(\circ\) CF868F Yet Another Minimization Problem
\(\circ\) P5574 [CmdOI2019]任务分配问题
\(\circ\) P4072 [SDOI2016]征途
0x03: 在 \(\boxed{\mathrm{1D/1D}}\) dp 中的运用
状态转移方程一般形如 \(f_i=\min\{f_{j-1}+w(j,i)\}\),也就是一个分段问题(不过段数不限),这类问题就不能使用分治(因为是同层转移),而是使用二分队列/二分栈维护决策点。
例题:
\(\circ\) P1912 [NOI2009] 诗人小G
设 \(S_i\) 表示前 \(i\) 句诗加上 \((i-1)\) 个空格的长度,则 \(w(j,i)=|S_i-S_{j-1}-1-L|^P\) 表示将从 \(j\) 到 \(i\) 的诗句单独分成一行的代价。
通过暴力发现 \(w\) 满足四边形不等式,考虑决策单调性优化。
我们维护最优决策点 \(p_i\) ,由于满足决策单调性,对于两个决策点 \(x,y\ (x<y)\),我们一定能找到个分界点 \(k\),使得在 \(k\) 之前(\(< k\))用 \(x\) 转移优于 \(y\),在 \(k\) 之后(\(\ge k\))用 \(y\) 转移优于 \(x\)。
于是我们可以维护一个三元组 \((l,r,x)\),表示在区间 \([l,r]\) 中用 \(x\) 转移较优。根据优劣,对决策点维护个单调队列。
具体地,假设当前在位置 \(i\),我们取队头为最优转移,则队头 \((l_{head},r_{head},q_{head})\) 出队的前提是 \(r_{head}<i\)。对于队尾的三元组 \((l_{tail},r_{tail},q_{tail})\),我们能踢掉他的前提是 \(q_{tail}\) 和 \(i\) 的分界点 \(k\le l_{tail}\)。插入 \(i\) 即插入 \((k+1,n,i)\)。
事实上也不用那么麻烦地维护个三元组,记录队列中相邻两点的分界点即可。
0x04:\(\boxed{\mathrm{1D/1D}}\) 斜率优化
若转移方程能简化成 \(f_i=\min/\max A_i\times B_j+C_i+D_j\),由于其中有一项与 \(i,j\) 都相关,那么就不适用于上面的优化方法。
先不考虑 \(\min/\max\),把相关的项放在一起得 \(D_j=A_i\times B_j+(C_i-f_i)\)。令 \(y=D_j,k=A_i,x=B_j,b=C_i-f_i\),则整个方程可转化成 \(y=kx+b\) 的形式(具体来说是把已知的 \(i\) 作为 \(k\),找到决策点 \(j\) 就是找到点 \((x,y)\),所以 \(x,y\) 只和 \(j\) 有关),其中 \(y\) 和 \(k\) 都是已知的,且 \(f_i=b+C_i\)。
那么我们只需用给定的斜率 \(k\) 找到一个点 \((x,y)\),使得经过此点的直线截距取到 \(\min/\max\) 即可。
例题:
容易写出转移方程(有做特殊处理):
转换成斜率优化的形式变成
也就是说对于给定的 \(k=2(s_i-L)\) 找到点 \((x,y)\) 满足要求即可。
斜率优化的关键就在此,如何快速地找到这个点呢?显然,我们将这条直线从很低的地方向上平移,碰到的第一个点即为最优,这些决策点即为下凸包上的点(如果要 \(\max\) 则反之从上往下,决策点为上凸包)。
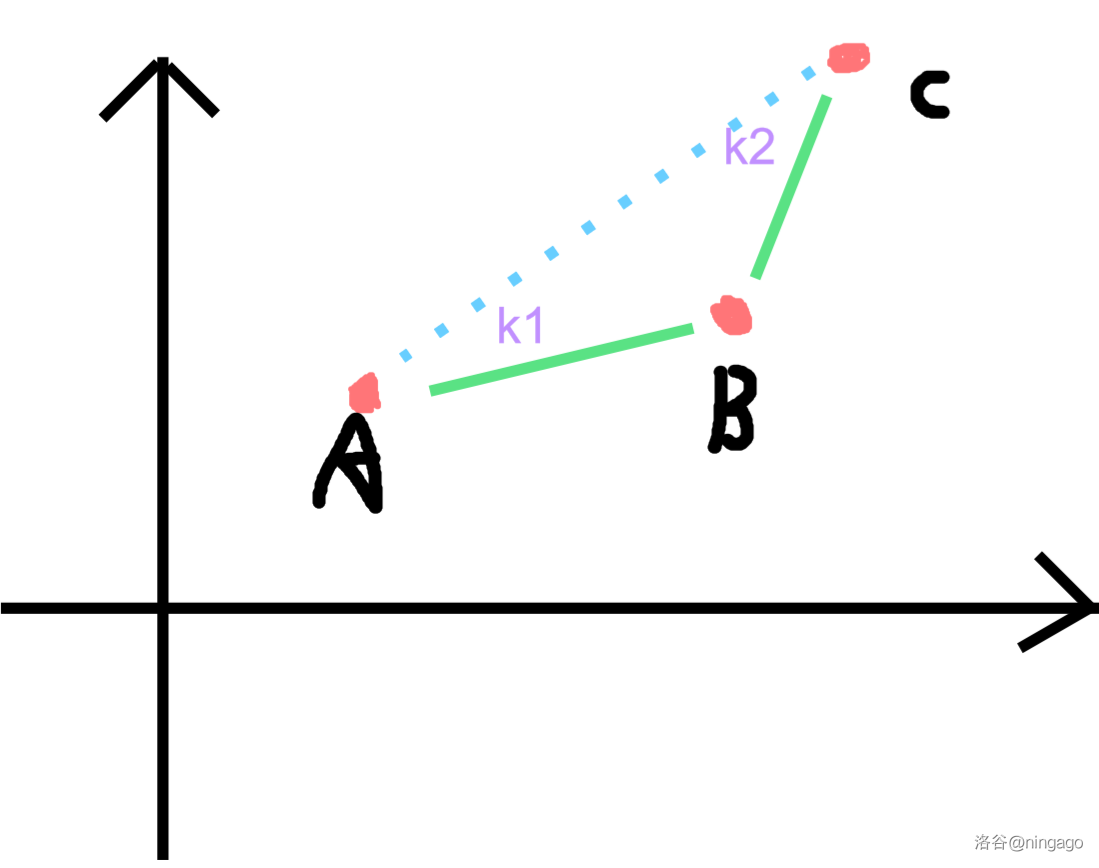
设最优决策点为 \(B\), 则对于给定的 \(k\) 显然有 \(k1< k < k2\) (不然就碰不到),而且每次查询的斜率 \(k\) 单调,那么我们可以对此用单调队列维护个下凸包,按照 \(k1< k < k2\) 淘汰头节点即可。
对于 \(k\) 不单调但是插入的点横坐标有序的情况,则用单调栈维护凸包,然后按照 \(k1< k < k2\) 二分即可。
对于 \(k\) 和横坐标都不单调的情况,可用动态凸包/李超树/CDQ 等解决。
2022.10.8 补充:对于维护的是上凸包,且 \(k,x\) 单增,应该用单调栈维护决策点,如 P5504 [JSOI2011] 柠檬。反之下凸包且 \(k\) 单减同理。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号