你所不了解的数据结构-van Emde Boas 树
前言
van Emde Boas 树(以下简称 vEB 树),是由荷兰计算机科学家 \(\mathtt{Peter\ van\ Emde\ Boas}\) 于 1975 年发明的一种树数据结构。
当我翻开 《算法导论》 的目录的时候,一下子就被这个奇特的名字吸引住了。在学习过程中,我发现这个数据结构构思极其巧妙。因此,我将按照原文的思路,采用更通俗易懂的表述介绍这个数据结构,这篇文章也是我的学习笔记。此外,网上有关 vEB 树的实现均为指针实现,我这里将会给出无指针的实现。
最后,这篇文章如果有什么疏漏或错误之处,还请读者指出。这篇文章仅作抛砖引玉啦~
\(0.\) 前置芝士
-
一定的树数据结构知识。
-
master 定理(分析时间复杂度的时候用)。
\(1.\) 引入
我们知道,像红黑树,二叉堆等支持优先队列操作的数据结构,它们的某些重要操作的时间复杂度的最坏(或摊还)情况的时间复杂度需 \(O(\log{n})\)。
在这篇文章里,我们会看到 vEB 树也支持优先队列和一些其他操作,分别是:查询元素是否存在、插入和删除元素、查询前驱和后继、查询集合里的最大值和最小值,且每个操作的时间复杂度都只需惊人的 \(O(\log{\log{n}})\)!!!但这个数据结构也有个限制,那就是所有关键字必须为 \([0,n-1]\) 的整数且无重复。
为避免歧义,以后我们用 \(n\) 表示元素个数,\(u\) 表示存储关键字值的全域大小(即关键字的值域为 \(\{0,1,2,...,u-1\}\))。其中,如无特殊要求,始终假定 \(u=\{2^k:k\in\mathbb{N}_+\}\)。那么 vEB 树的每一个操作的时间复杂度都为 \(O(\log{\log{u}})\)。
\(2.\) 简单的思路
由于我们只存储关键字的值域,可以开一个桶。若元素 \(i\) 存在,则 \(A[i]=1\),反之 \(A[i]=0\)。这样,查询元素是否存在、插入和删除元素的操作只需要 \(O(1)\),但查询前驱和后继、查询集合内最大值和最小值的操作最坏需要 \(O(u)\),因为我们需要扫描所查询元素前(后)面的所有元素,直到找到第一个存在的元素为止。
\(2.1\) 叠加结构
前面讲到,如果单开一个桶,查询前驱和后继扫描的时间将会非常久。那么,如何缩短扫描的时间呢?
我们考虑在桶上叠加一棵二叉树,如图:
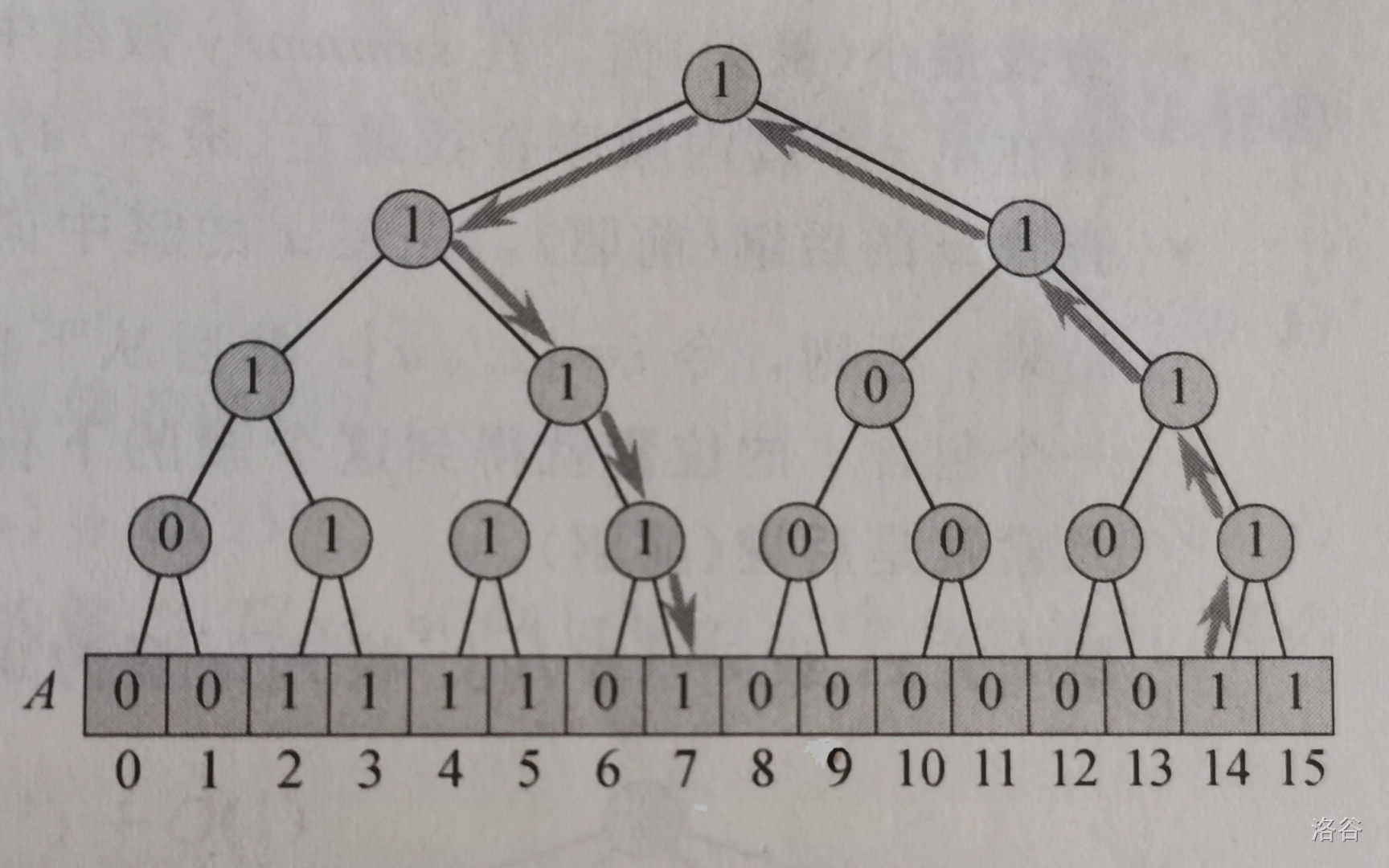
其中每一个非叶结点都代表一段值域的元素,其值为两个儿子的逻辑或,表示其代表的值域是否存在元素。我们来看看如何实现操作:
-
查询最大值:从根节点出发,一直走最右边的非零结点。
-
查询最小值:从根节点出发,一直走最左边的非零结点。
-
查询某个元素的前驱:从该元素出发,一直向上走,直到从右边进入某个结点,且该结点的左儿子非零,查询以该左儿子为根的最大值。(图中即为查询 \(14\) 的前驱的过程)
-
查询某个元素的后继:从该元素出发,一直向上走,直到从左边进入某个结点,且该结点的右儿子非零,查询以该右儿子为根的最小值。
-
插入某个元素:从根节点(或该元素)出发,把从根节点到该元素的路径上的每个结点都赋值为 \(1\)。
-
删除某个元素:将该元素的值置为 \(0\),然后从该元素开始,重新计算每个结点的或值(因为它的兄弟结点有可能非零,所以删掉这个元素后,其父节点不一定为 \(0\))。
我们会发现,除了查询一个元素是否存在(直接查桶 \(O(1)\))外,其他操作都是 \(O(\log{u})\)(因为只需要遍历二叉树上的一个路径),这很好地降下了复杂度。
旁白:???\(O(\log u)\)?我要的 \(O(\log{\log{u}})\) 呢!(恼
别着急,慢慢来嘛~
\(2.2\) 簇
有的时候,我们不一定要二叉树,我们可以像 B 树一样,使用多叉的结构。这样,整棵树的高度就减小了许多。
我们令值域 \(u=\{2^{2k}:k\in \mathbb{Z}\}\),那么 \(\sqrt{u}\) 是个整数。我们叠加一颗 \(\sqrt{u}\) 叉树,来代替二叉树,如图
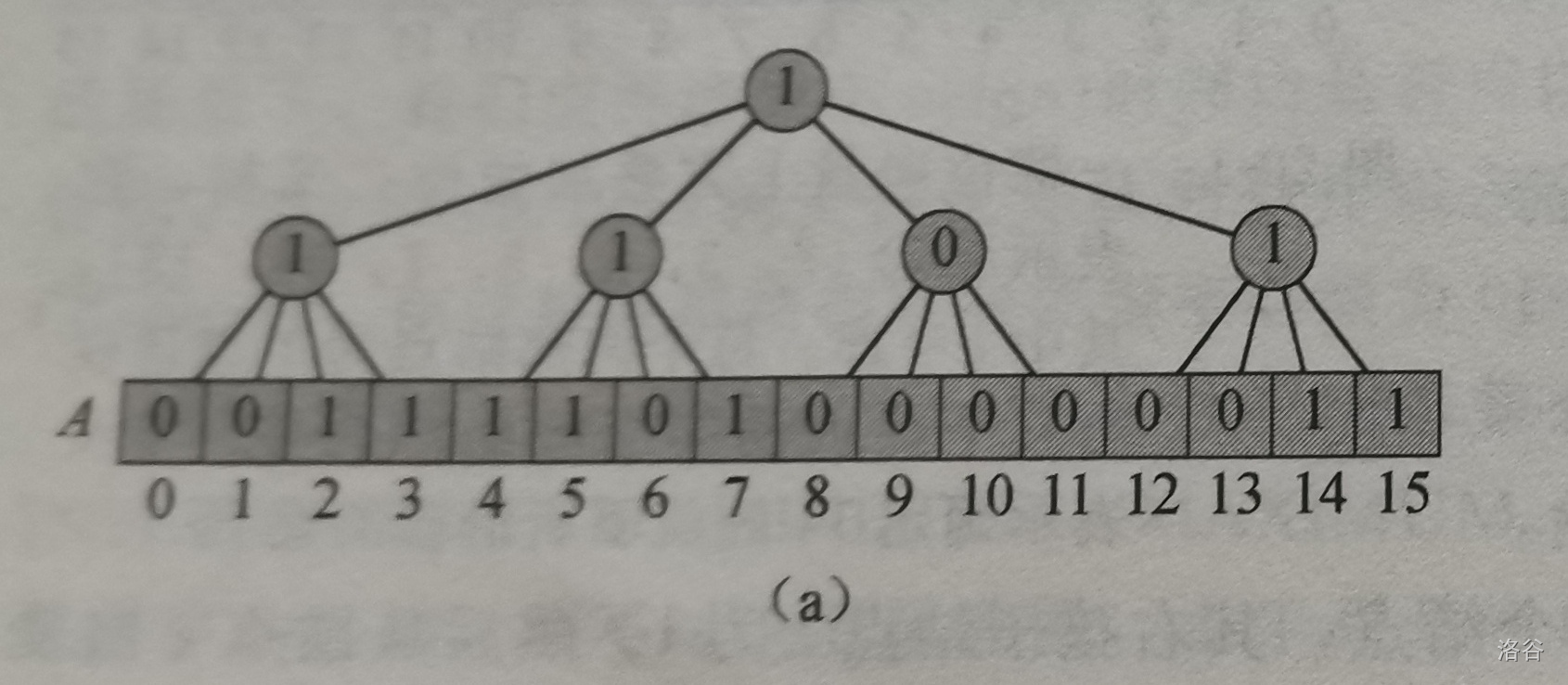
同样地,每一个非叶结点都代表一段值域的元素,其值为所有儿子的逻辑或。我们可以把这些非叶节点定义成一个数组 \(summary\),其中 \(summary[i]\) 为 \(1\) 则代表着其子节点有 \(1\),我们称 \(summary[i]\) 为第 \(i\) 个簇。如图
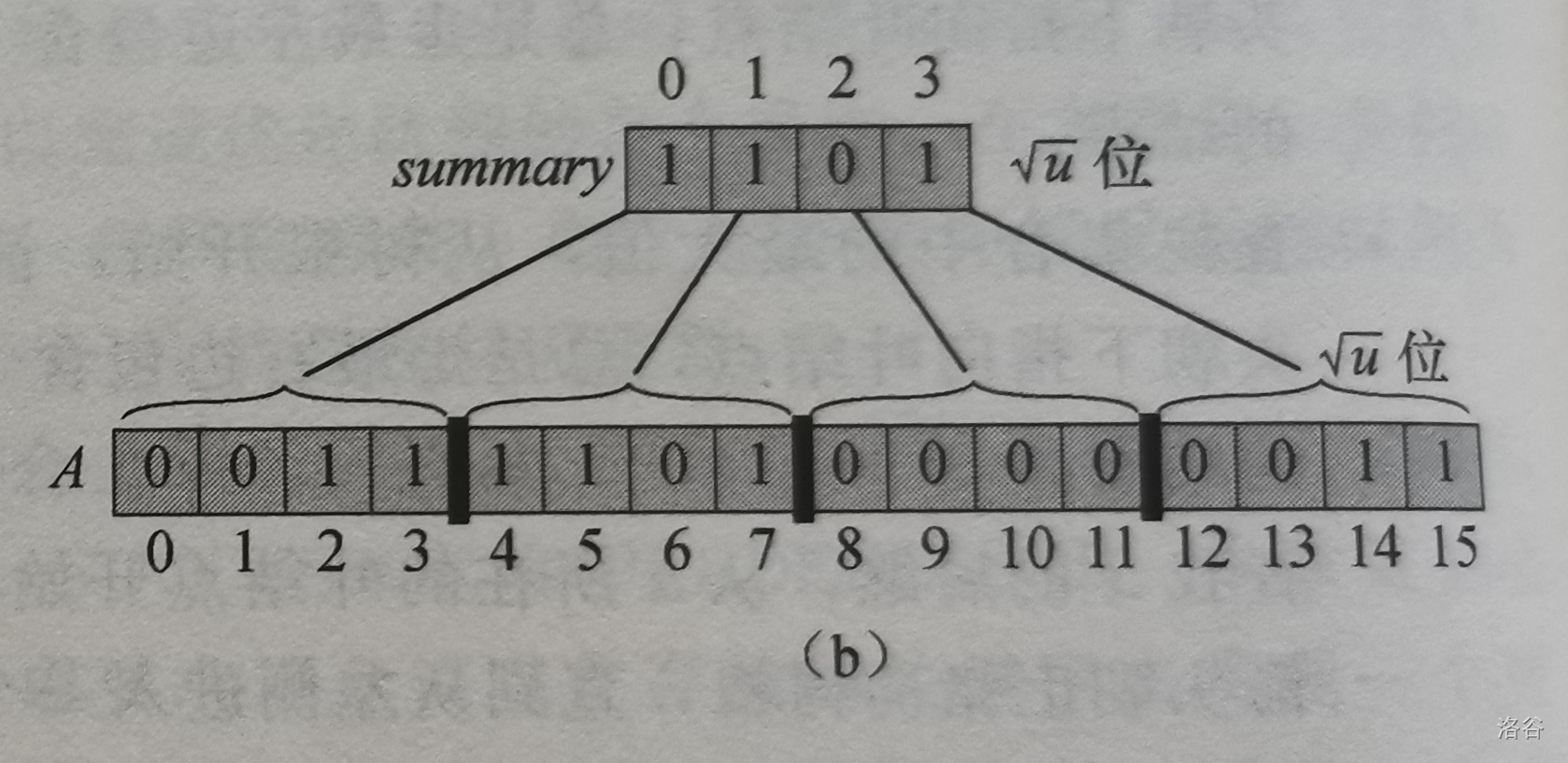
我们来考虑一下如何实现一些操作:
-
查询最大值:在 \(summary\) 中查找最右边为 \(1\) 的簇,再查询该簇内最右边为 \(1\) 的元素。
-
查询最小值:在 \(summary\) 中查找最左边为 \(1\) 的簇,再查询该簇内最左边为 \(1\) 的元素。
-
查询某个元素的前驱:在该元素所在簇中向左找,如果有 \(1\) 则为结果,否则在 \(summary\) 中从该簇向左找,如果有为 \(1\) 的簇则返回这个簇的最大值。
-
查询某个元素的后继:在该元素所在簇中向右找,如果有 \(1\) 则为结果,否则在 \(summary\) 中从该簇向右找,如果有为 \(1\) 的簇则返回这个簇的最小值。
-
插入一个元素:置该元素和该元素所在簇为 \(1\)。
-
删除一个元素:置该元素为 \(0\),重新计算该元素所在簇的逻辑或。
我们可以发现,除了插入和查询某个元素是否存在(都是 \(O(1)\))外,其他操作的时间复杂度都为 \(O(\sqrt{u})\)。
旁白:???\(O(\sqrt{u})\)?好像更慢了啊喂!
虽然慢,但这个思想为后续 vEB 树的讲解奠定了重要的基础。
\(3.\) 原型 vEB 树
本节中假设 \(u=\{2^{2^k}:k\in\mathbb{Z}\}\),则有 \(u^{\frac{1}{2}},u^{\frac{1}{4}}\) 等都为整数。
另外,从这节开始,有操作的部分我将会附上代码。
\(3.1\) 定义
-
\(high(x)=\lfloor{x/\sqrt{u}}\rfloor\)
-
\(low(x)=x\bmod \sqrt{u}\)
-
\(index(x,y)=x\sqrt{u}+y\)
这里一一来解释一下:为什么是 \(\sqrt{u}\) 呢?因为值域为 \(u\),每个簇的大小就为 \(\sqrt{u}\)。 \(high(x)\) 表示的是值 \(x\) 所在簇的编号;\(low(x)\) 表示的是值 \(x\) 在所在簇里面的编号;\(index(x,y)\) 则表示第 \(x\) 个簇的第 \(y\) 个元素是什么。(注意:编号也是从 \(0\) 开始的,这里所说的第 \(x\) 个簇指的是下面要讲的结构内的簇编号)那么我们就有 \(x=index(high(x),low(x))\)。
\(3.2\) 结构
我们考虑一种递归结构,像上面的大小为 \(\sqrt{u}\) 的 \(summary\) 数组一样,其每一个元素都指向一个大小为 \(\sqrt{u}\) 的结构。也就是说,一个大小为 \(u^{\frac{1}{2}}\) 的结构,包含着 \(u^{\frac{1}{2}}\) 个大小为 \(u^{\frac{1}{4}}\) 的结构,其又包含着 \(u^{\frac{1}{4}}\) 个大小为 \(u^{\frac{1}{8}}\) 的结构,直到大小为 \(2\) ,我们称它为基本结构。
像这样的的结构 我们定义它为原型 vEB 结构(proto_vEB)。(至于为什么是原型是因为它与真正的 vEB 结构还有区别)
下图就是一个原型 vEB 结构:
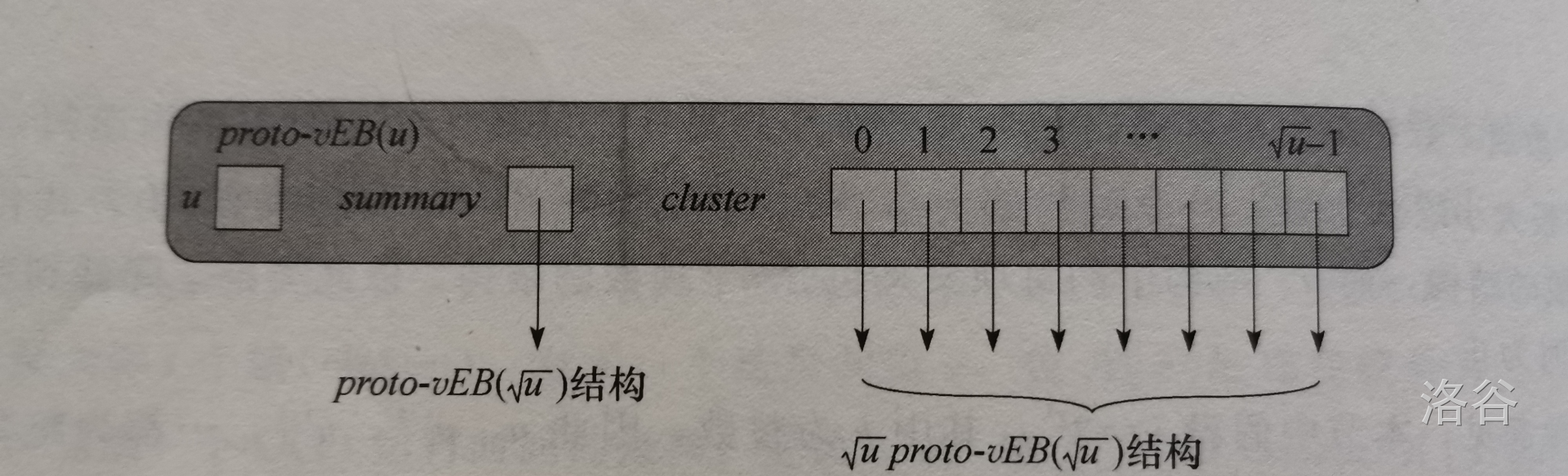
其中 \(u\) 代表该结构的值域大小,我们称一个值域为 \([0,u-1]\) 的原型 vEB 结构为 \(proto\_vEB(u)\)。当 \(u=2\) 时,这个结构是个基本结构,只包含 \(A[0,1]\),也就是只存储两个元素的信息。当 \(u\not=2\) 时,它包含着以下特征:
-
包含 \(\sqrt u\) 个簇的 \(cluster\) 数组,每一项分别指向一个 \(proto\_vEB(\sqrt u)\) 结构,分成更小的结构(也就是更小的簇)。
-
一个 \(summary\) 指针,它指向一个 \(proto\_vEB(\sqrt u)\) 结构,这个结构存储了 \(\sqrt u\) 个簇的所有信息,也就是它们的逻辑或。
结构体以及定义的实现:
struct proto_vEB{
int u;
bool A[2];//基本结构
int summary;
vector<int>cluster;
//用int是因为我之后建树将使用无指针
//vector是因为怕炸空间(
}tre[MAXN];
inline int high(int p,int x){
int u=(int)sqrt(tre[p].u);
return x/u;
}
inline int low(int p,int x){
int u=(int)sqrt(tre[p].u);
return x%u;
}
inline int index(int p,int x,int y){
int u=(int)sqrt(tre[p].u);
return x*u+y;
}
我们把这些结构组合起来,就形成了一个原型 vEB 树:
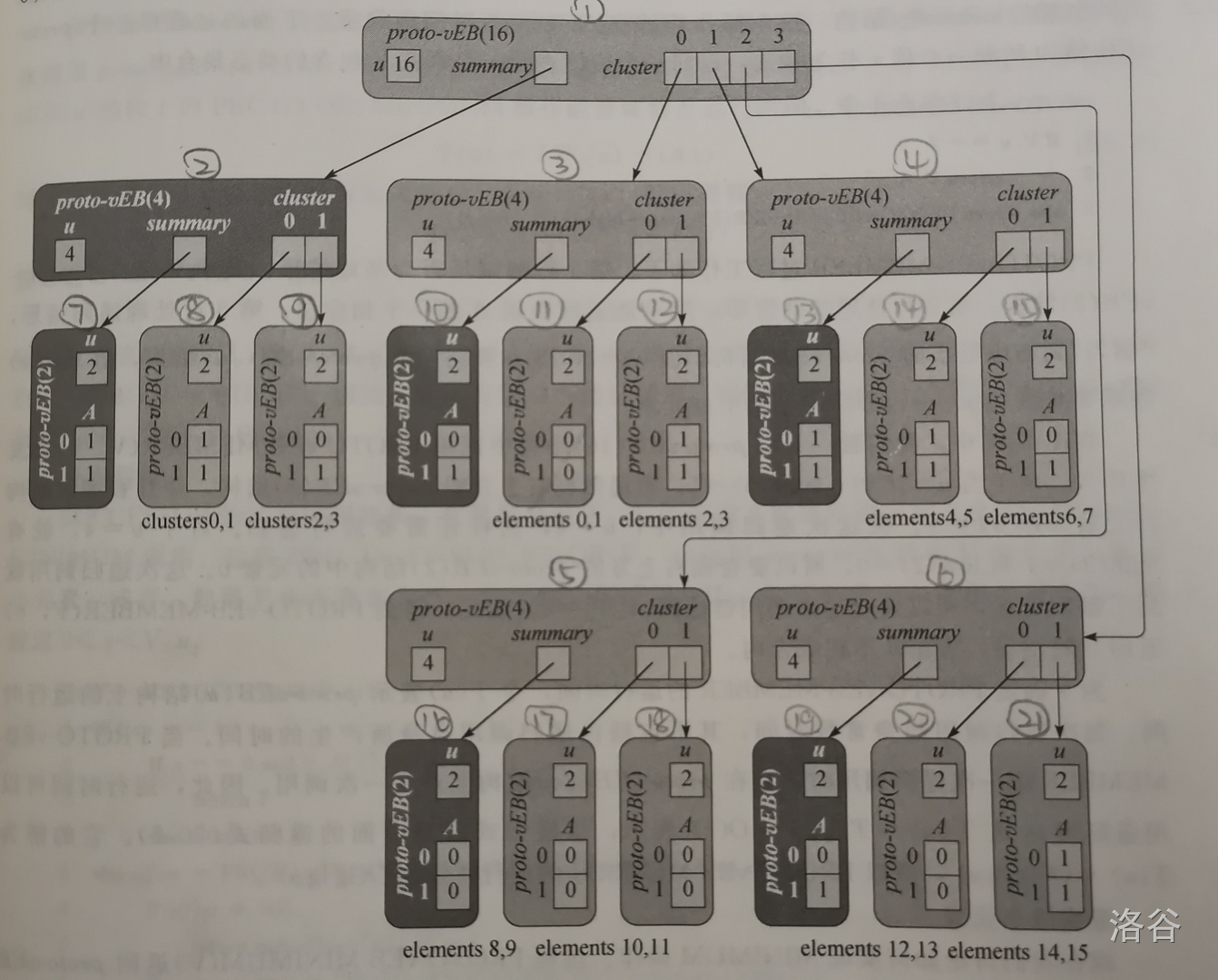
是不是很眼花缭乱?为了方便说明,我给每一个结构都编了序号(注意编号和序号的区分)。
这个 \(proto\_vEB(16)\) 结构存储的元素集合有 \(\{2,3,4,5,7,14,15\}\),存储它们的基本结构的序号为 \(12,14,15,21\)。我们可以发现,序号为 \(10\) 的 \(summary\) 结构存储了序号为 \(11,12\) 的基本结构的信息,其中 \(A[1]=1\) 表示序号为 \(12\) 的基础结构中有元素存在;序号为 \(9\) 的基本结构存储了序号为 \(5,6\) 的簇结构的信息(因为序号为 \(9\) 的结构是属于一个 \(summary\) 里的),其中 \(A[0]=0\) 表示序号为 \(5\) 的簇结构内没有任何元素存在;同理,序号为 \(7\) 的 \(summary\) 结构又存储了序为 \(8,9\) 的基本结构的信息。
这里我还要补充一下上面 \(index(x,y)\) 的定义,对于一个元素 \(a\),它在包含它的不同结构里的编号不一定相同,如:元素 \(7\) 在序号为 \(15\) 的 \(proto\_vEB(2)\) 结构中的编号为 \(1\),但它在序号为 \(4\) 的 \(proto\_vEB(4)\) 结构中的编号为 \(3\)。\(index\) 不仅仅是指一个元素的编号,也可以指一个结构在 \(summary\) 的编号,如:序号为 \(5\) 的 \(proto\_vEB(4)\) 结构在序号为 \(9\) 的 \(proto\_vEB(2)\) 结构(它属于 \(summary\))中的编号为 \(0\),在序号为 \(7\) 的 \(proto\_vEB(2)\) 结构中的编号为 \(2\)。
讲到这里可能会有点乱,建议反复看几次加强理解。
\(3.3\) proto_vEB 操作实现
在讲操作之前,我要给出两个递归式,并根据《算法导论》给出解法,这两个递归式是后续操作计算时间复杂度时的两种情况:
递归式一:
考虑变量替换法,令 \(m=\log u\),则 \(u=2^m\),有
重命名 \(S(m)=T(2^m)\),则新的递归式为
根据 master 定理解得 \(S(m)=O(\log m)\),则
递归式二:
同样考虑变量替换法,令 \(m=\log u\),则有
重命名 \(S(m)=T(2^m)\),得
根据 master 定理解得 \(S(m)=O(m)\),则
好啦,我们可以开始操作讲解啦!
\(3.3.1\) 判断某个值是否在集合中
bool PROTO_vEB_MEMBER(int p,int x){
if(tre[p].u==2)return tre[p].A[x];
return PROTO_vEB_MEMBER(tre[p].cluster[high(p,x)],low(p,x))
}
这个很简单,如果是基本结构直接返回 \(A\) 数组内对应的值,否则递归查询更小的结构。由于只产生了一次递归调用,这个过程我们可以写成递归式一,时间复杂度为 \(O(\log\log u)\)。
\(3.3.2\) 插入某个元素
void PROTO_vEB_INSERT(int p,int x){
if(tre[p].u==2)tre[p].A[x]=1;
else {
PROTO_vEB_INSERT(tre[p].cluster[high(p,x)],low(p,x));
PROTO_vEB_INSERT(tre[p].summary,high(p,x));
}
}
这个也很简单,如果是基本结构直接置 \(A\) 数组对应的值为 \(1\),否则递归插入。注意,我们不仅要把该值插入到簇里面,还要把相应的簇插入到 \(summary\) 里面以表示簇内有元素。此过程调用了两次递归,可以写成递归式二,时间复杂度 \(O(\log u)\)。
\(3.3.3\) 删除某个元素
这个相比于插入要复杂的多,我们需要判断簇中还有没有元素,可以添加属性 \(num\) 表示该簇内拥有的元素个数(这个操作《算法导论》里居然没给伪代码,可恶不能当懒人了)。相应地,我们的插入也要修改一下。
int PROTO_vEB_INSERT(int p,int x){//不保证x一定在集合内
if(tre[p].u==2){
if(!tre[p].A[x]){
++tre[p].num;
tre[p].A[x]=true;
return 1;
}
return 0;
}
int tmp1=PROTO_vEB_INSERT(tre[p].cluster[high(p,x)],low(p,x)),tmp2=PROTO_vEB_INSERT(tre[p].summary,high(p,x));
tre[tre[p].cluster[high(p,x)]].num+=tmp1;
tre[tre[p].summary].num+=tmp2;
return tmp1+tmp2;
}
int PROTO_vEB_DELETE(int p,int x){//保证x一定在集合内
if(tre[p].u==2){
--tre[p].num;tre[p].A[x]=0;
return 1;
}
int tmp1=PROTO_vEB_DELETE(tre[p].cluster[high(p,x)],low(x)),tmp2=0;
tre[p].num-=tmp1;
if(!tre[p].num){
tmp2=PROTO_vEB_DELETE(tre[p].summary,high(p,x));
tre[tre[p].summary].num-=tmp2;
}
return tmp1+tmp2;
}
我们发现,两个函数的返回值都是int,它们分别表示什么意思呢?
插入中的返回值表示的是新插入的元素的个数,同样,删除中的返回值表示的就是删除的元素的个数。
插入的部分很容易懂我就不讲了,看看删除。如果是基本结构,删除了数之后直接返回 \(1\),否则,先从簇里删除这个数,如果删掉该数后簇为空,我们再从 \(summary\) 里面删掉这个簇。最后返回删掉的元素的个数。
考虑最坏情况,删除的过程要调用两次函数,可以用递归式二表示,时间复杂度 \(O(\log u)\)。
\(3.3.4\) 查询最小值
这里的查询最小值表示的是查询某个结构中的最小值。
int PROTO_vEB_MINIMUM(int p){
if(tre[p].u==2){
if(tre[p].A[0])return 0;
if(tre[p].A[1])return 1;
return NIL;
}
int min_cluster=PROTO_vEB_MINIMUM(tre[p].summary);
if(min_cluster==NIL)return NIL;
int offset=PROTO_vEB_MINIMUM(tre[p].cluster[min_cluster]);
return index(min_cluster,offset);
}
如果是基本结构就返回里面最小的,如果这个基础结构不包含任何元素则返回 \(NIL\)。否则,先从 \(summary\) 查询最小的簇,再从这个簇里面查询。如果没有最小的簇,也就是 \(summary\) 中不包含任何元素,则返回 \(NIL\),否则返回最小值的编号。
这个操作需要调用两次递归,为递归式二,时间复杂度 \(O(\log u)\)。
由于查询最大值操作是对称的,这里就不赘述。
\(3.3.5\) 查询后继
int PROTO_vEB_SUCCESSOR(int p,int x){
if(tre[p].u==2){
if(x==0&&tre[p].A[1])return 1;
return NIL;
}
int offset=PROTO_vEB_SUCCESSOR(tre[p].cluster[high(p,x)],low(p,x));
if(offset!=NIL)return index(p,high(p,x),offset);
int succ_cluster=PROTO_vEB_SUCCESSOR(tre[p].summary,high(p,x));
if(succ_cluster==NIL)return NIL;
offset=PROTO_vEB_MINIMUM(tre[p].cluster[succ_cluster])return index(p,succ_cluster,offset);
}
如果是基本结构,判断查询的值是不是前一个元素且后一个元素存在,否则返回 \(NIL\)。不是基本结构的话,首先先看查询元素所在的簇中存不存在后继,不存在的话就在 \(summary\) 里面查询这个簇的后继簇,最后返回簇中最小值。
这里的时间复杂度比较特殊,我们需要调用两次查询后继的函数和一次最小值函数,可以列出这样的递归式:
还是变量替换法,令 \(m=\log u\),则有
重命名 \(S(m)=T(2^m)\),得
根据 master 定理解得 \(S(m)=O(m\log m)\),则
查询前驱操作也是对称的,这里也不赘述。
至此,原型 vEB 树的部分已经讲完。虽然原型 vEB 树的效率已经很好,但是还没全部达到预期的 \(O(\log\log u)\)。接下来,我们将会看到真正的 vEB 树是如何将这些操作优化至 \(O(\log\log u)\)的。
\(4.\) 真正的 vEB
还记得第 \(3\) 节中的假设吗?\(u=2^{2^k}\),这个假设局限性太大了。在真正的 vEB 里,我们允许 \(u=\{2^k:k\in\mathbb{N}_+\}\),但这样,\(\sqrt u\) 就不一定是整数了。
这里我们记 \(2^{\lceil\frac{\log u}{2}\rceil}=^\uparrow\!\!\!\!\!\sqrt u\),\(2^{\lfloor\frac{\log u}{2}\rfloor}=^\downarrow\!\!\!\!\!\sqrt u\)(这 LaTex 有够难打的),即 \(u\) 的上、下平方数(有 \(u=^\uparrow\!\!\!\!\!\sqrt u\times^\downarrow\!\!\!\!\!\sqrt u\))。那么,我们之前定义的函数也要有所修改:
-
\(high(x)=\lfloor{x/\ ^\downarrow\!\!\!\!\sqrt{u}}\rfloor\)
-
\(low(x)=x\bmod\ ^\downarrow\!\!\!\!\sqrt{u}\)
-
\(index(x,y)=x\ \ ^\downarrow\!\!\!\!\sqrt{u}+y\)
\(4.1\) 结构
vEB 的结构是以 proto_vEB 为基础修改而来,我们称一个大小为 \(u\) 的 vEB 结构为 \(vEB(u)\)。由于 \(u\) 发生了变化,在非基础结构中,\(summary\) 指向一个 \(vEB(\ ^\uparrow\!\!\!\!\sqrt u)\) 结构,\(cluster\) 数组则包含了 \(\ ^\uparrow\!\!\!\!\sqrt u\) 个簇,每个簇都分别指向一个 \(vEB(\ ^\downarrow\!\!\!\!\sqrt{u})\) 结构。
除此之外,我们还新增了两个属性:
-
\(min:\) 表示该结构内的最小元素。
-
\(max:\) 表示该结构内的最大元素。
如图就是一个 vEB 结构:
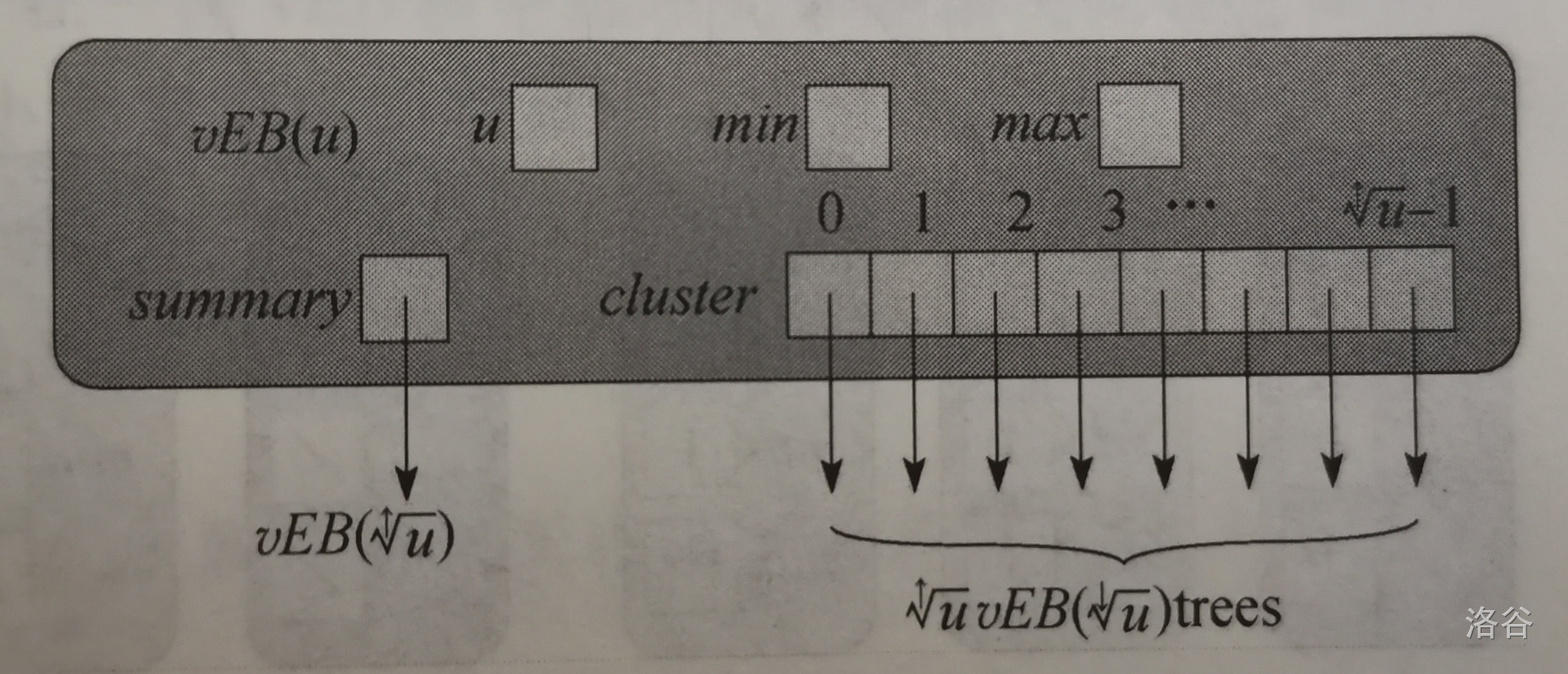
结构体和定义:
map<int,int>lg;
struct vEB{
int u,summary;
vector<int>cluster;
int min,max;
}vEB[MAXN];
void init(){
for(int i=0;i<32;++i)lg[1<<i]=i;//预处理log
}
inline int high(int p,int x){
int u=1<<(lg[vEB[p].u]>>1);
return x/u;
}
inline int low(int p,int x){
int u=1<<(lg[vEB[p].u]>>1);
return x%u;
}
inline int index(int p,int x,int y){
int u=1<<(lg[vEB[p].u]>>1);
return x*u+y;
}
特别地,我们有一些性质:
-
\(min\) 中存储的元素一定不会在该结构的所有簇中出现(\(max\) 不一定)。
-
如果是基础结构,那么我们不再需要用 \(A\) 数组,可以直接使用 \(min\) 和 \(max\) 表示(如果只有一个元素,则 \(min\) 和 \(max\) 都为它,如果没有元素的话,\(min\) 和 \(max\) 都为 \(NIL\))。
-
通过 \(min\) 和 \(max\),我们可以在常数时间内知道一个结构是否为空,或者仅含一个或两个以上的元素,可以缩短插入、删除、前驱、后继的递归调用链。
以下就是一棵标准的 vEB,其表示的集合跟之前 proto_vEB 的图一样,上述的性质均可在里面体现。
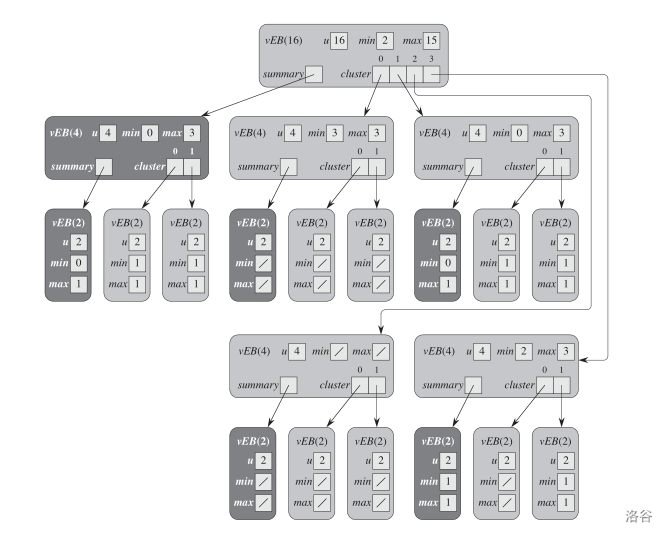
\(4.2\) 操作
下面我还是要给出一个递归式,根据《算法导论》给出解法,对于 vEB 的所有递归过程的操作的时间复杂度,我们都可以用下面的式子表示。
令 \(m=\log u\),则有
注意到,对于所有的 \(m\geq2\),都有 \(\lceil\frac{m}{2}\rceil\leq \frac{2m}{3}\),可以得到
重命名 \(S(m)=T(2^m)\),则重写为
根据 master 定理,有解 \(S(m)=O(\log m)\),所以我们有
\(T(u)=T(2^m)=S(m)=O(\log m)=O(\log\log u)\)
\(4.2.1\) 判断某元素是否在集合中
bool Tree_Member(int p,int x){
if(x==vEB[p].min||x==vEB[p].max)return true;
if(vEB[p].u==2)return false;
return Tree_Member(vEB[p].cluster[high(p,x)],low(p,x));
}
第一句话就是缩短运行时间的,如果 \(x\) 是最大或最小值,直接返回。如果既不是最大值也不是最小值,且该结构还是基本结构的话,\(x\) 一定不存在(因为基本结构就这两种元素),否则还是递归。时间复杂度 \(O(\log\log u)\)。
\(4.2.2\) 查询最大/小值
inline int Tree_Minimum(int p){
return vEB[p].min;
}
inline int Tree_Maximum(int p){
return vEB[p].max;
}
这个不用说了吧,\(O(1)\) 解决。
\(4.2.3\) 查询后继
int Tree_Successor(int p,int x){
if(vEB[p].u==2){
if(x==0&&vEB[p].max==1)return 1;
return NIL;
}
if(vEB[p].min!=NIL&&x<vEB[p].min)return vEB[p].min;
int offset,max_low=Tree_Maximum(vEB[p].cluster[high(p,x)]);
if(max_low!=NIL&&low(p,x)<max_low){
offset=Tree_Successor(vEB[p].cluster[high(p,x)],low(p,x));
return index(p,high(p,x),offset);
}
int succ_cluster=Tree_Successor(vEB[p].summary,high(p,x));
if(succ_cluster==NIL)return NIL;
offset=Tree_Minimum(vEB[p].cluster[succ_cluster]);
return index(p,succ_cluster,offset);
}
判断基础结构的语句和原型一样。注意到,如果 \(x\) 严格小于结构内的最小值,则直接返回,这确实省了不少时间。如果这些情况都不满足,我们先判断 \(x\) 所在簇内是否有后继,可以查询簇内最大值 \(O(1)\) 确定,有的话直接确定位置然后返回,没有的话再继续查询 \(summary\) 内 \(x\) 所在簇是否有后继,有则返回该后继的最小值。
整个过程最多只会调用一次递归,原先查询簇内是否有后继和查询后继簇的最小值的 \(O(\log u)\) 步骤都用 \(O(1)\) 的最大/小值函数代替了,时间复杂度 \(O(\log\log u)\)。
\(4.2.4\) 查询前驱
为什么前驱不和后继一起讲呢?因为前驱函数大体和后继函数是对称的,但是多加了一个判断:
int Tree_Predecessor(int p,int x){
if(vEB[p].u==2){
if(x==1&&vEB[p].min==0)return 0;
return NIL;
}
if(vEB[p].max!=NIL&&x>vEB[p].max)return vEB[p].max;
int offset,min_low=Tree_Minimum(vEB[p].cluster[high(p,x)]);
if(min_low!=NIL&&low(p,x)>min_low){
offset=Tree_Predecessor(vEB[p].cluster[high(p,x)],low(p,x));
return index(p,high(p,x),offset);
}
int pred_cluster=Tree_Predecessor(vEB[p].summary,high(p,x));
if(pred_cluster==NIL){
if(vEB[p].min!=NIL&&x>vEB[p].min)return vEB[p].min;
return NIL;
}
offset=Tree_Maximum(vEB[p].cluster[pred_cluster]);
return index(p,pred_cluster,offset);
}
这一句判断出现在第 \(13\) 行:
if(vEB[p].min!=NIL&&x>vEB[p].min)return vEB[p].min;
还记得之前说到的性质吗,\(min\) 中存在的元素不会出现在该结构的任何一个簇里,这里 \(pred\_cluster\) 的值为 \(NIL\),说明找不到前驱,但是还有一种可能,就是前驱就是 \(min\),这里就判断了这种情况。时间复杂度还是 \(O(\log\log u)\)。
\(4.2.5\) 插入一个元素
在原型 vEB 里,插入需要两次递归:往簇里插入元素,将簇插入到 \(summary\) 中。我们来思考一下,怎么样才能只用一次递归呢?
答案很简单,当该簇中有元素时,说明该簇已经存在于 \(summary\) 中,不需要再递归;当该簇为空时,我们直接把元素 \(O(1)\) 塞给 \(min\) 和 \(max\) 就行,然后递归将这个簇插入到 \(summary\) 里面。这样就做到了只用一次递归。
inline void Empty_Tree_Insert(int p,int x){
vEB[p].max=vEB[p].min=x;
}
void Tree_Insert(int p,int x){
if(vEB[p].min==NIL){
Empty_Tree_Insert(p,x);
return;
}
if(x<vEB[p].min)swap(x,vEB[p].min);
if(vEB[p].u>2){
if(Tree_Minimum(vEB[p].cluster[high(p,x)])==NIL){
Tree_Insert(vEB[p].summary,high(p,x));
Empty_Tree_Insert(vEB[p].cluster[high(p,x)],low(p,x));
}else Tree_Insert(vEB[p].cluster[high(p,x)],low(p,x));
}
if(x>vEB[p].max)vEB[p].max=x;
return;
}
如果 \(min\) 值为 \(NIL\),则显然这个簇是没有任何元素的,直接 \(O(1)\)。同时我们要满足性质,如果插入的值比当前最小值还小,那么就交换一下就行了,因为 \(min\) 不会出现在后面任何簇里,我们就改为插入之前的 \(min\) 就行。接着就按照上面刚刚讲的来执行就行。最后还要判断一下有没有插入最大值。全程最多调用一次递归, \(O(\log\log u)\)。
\(4.2.6\) 删除一个元素
所有操作里面最难理解的来了哦。
void Tree_Delete(int p,int x){//保证x存在于集合中
if(vEB[p].min==vEB[p].max){
vEB[p].min=vEB[p].max=NIL;
return;
}
if(vEB[p].u==2){
vEB[p].max=vEB[p].min=!x;
return;
}
if(x==vEB[p].min){
int first_cluster=Tree_Minimum(vEB[p].summary);
x=index(p,first_cluster,Tree_Minimum(vEB[p].cluster[first_cluster]));
vEB[p].min=x;
}
Tree_Delete(vEB[p].cluster[high(p,x)],low(p,x));
if(Tree_Minimum(vEB[p].cluster[high(p,x)])==NIL){
Tree_Delete(vEB[p].summary,high(p,x));
if(x==vEB[p].max){
int summary_max=Tree_Maximum(vEB[p].summary);
if(summary_max==NIL)vEB[p].max=vEB[p].min;//如果summary里面为空,那么剩下的就只有min了(就算min的值为NIL也直接赋值给max)
else vEB[p].max=index(p,summary_max,Tree_Maximum(vEB[p].cluster[summary_max]));//否则重新设置max
}
}else if(x==vEB[p].max)vEB[p].max=index(p,high(p,x),Tree_Maximum(vEB[p].cluster[high(p,x)]));
return;
}
首先确定结构内元素的个数,如果只有一个,像第一句判断一样,直接就删除了,否则结构内至少有两个元素。如果是基础结构(两个元素),那么置 \(min\) 和 \(max\) 为另外一个就行。接下来就是非基础结构的情况了。
首先考虑如果删除的是 \(min\),根据性质,我们只需要直接找到第二小的元素给他替换上就行。
然后我们递归删除簇内的这个元素,如果删掉后簇为空了,那么就从 \(summary\) 里面删掉这个簇。再来考虑删掉的是最大值的情况,我们只要找到第二大的替换上去就行。为什么调用最大值函数一定就是第二大呢?因为 \(x\) 既是簇里的最大值,又是簇里的唯一一个元素,删掉了它,又删掉了簇,剩下的不就是第二大了嘛,其余部分看注释。
如果删掉 \(x\) 后簇没空,再考虑删去的是最大值的情况,因为前面已经调用了删去 \(x\) 的函数,那么剩下的肯定是第二大,直接替换上去就行。
乍一看,删除函数里面最多会调用两次递归,但是注意调用的条件:我们调用第二次递归的前提是 \(x\) 是簇里唯一的元素,既然是唯一的,那么删除它的时候会在第一个判断的时候 \(O(1)\) 判断掉。所以只会有两种可能:
-
第一次调用只用 \(O(1)\)。
-
第二次调用不会发生。
所以删除操作的时间复杂度还是 \(O(\log\log u)\) 的。
终于讲完啦!
\(5.\) 例题
\(O(\log\log u)\) 的时间复杂度处理 \(10^6\) 的数据还是游刃有余的,但唯一的缺点就是建树的时间是 \(O(u)\) 的,如果操作过少,值域过大,效率可能比其它树数据结构还低。
\(Code:\)
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e6,NIL=-1;
int cnt;
map<int,int>lg;
struct vEB{
int u,summary;
vector<int>cluster;
int min,max;
}vEB[MAXN];
inline void Tree_Build(int p,int size){//u=2^size
vEB[p].summary=vEB[p].min=vEB[p].max=NIL;
if(size<=1){
vEB[p].u=2;return;
}
vEB[p].u=1<<size;
int cluster_size=(size>>1)+(size&1);//即ceil(log(u)/2)
vEB[p].summary=++cnt;
Tree_Build(vEB[p].summary,cluster_size);
vEB[p].cluster.resize(1<<cluster_size); //节省空间用的
for(int i=0;i<1<<cluster_size;++i){
vEB[p].cluster[i]=++cnt;
Tree_Build(vEB[p].cluster[i],size>>1);
}
return;
}
void init(){
for(int i=0;i<32;++i)lg[1<<i]=i;
}
inline int high(int p,int x){
int u=1<<(lg[vEB[p].u]>>1);
return x/u;
}
inline int low(int p,int x){
int u=1<<(lg[vEB[p].u]>>1);
return x%u;
}
inline int index(int p,int x,int y){
int u=1<<(lg[vEB[p].u]>>1);
return x*u+y;
}
inline int Tree_Minimum(int p){
return vEB[p].min;
}
inline int Tree_Maximum(int p){
return vEB[p].max;
}
bool Tree_Member(int p,int x){
if(x==vEB[p].min||x==vEB[p].max)return true;
if(vEB[p].u==2)return false;
return Tree_Member(vEB[p].cluster[high(p,x)],low(p,x));
}
int Tree_Successor(int p,int x){
if(vEB[p].u==2){
if(x==0&&vEB[p].max==1)return 1;
return NIL;
}
if(vEB[p].min!=NIL&&x<vEB[p].min)return vEB[p].min;
int offset,max_low=Tree_Maximum(vEB[p].cluster[high(p,x)]);
if(max_low!=NIL&&low(p,x)<max_low){
offset=Tree_Successor(vEB[p].cluster[high(p,x)],low(p,x));
return index(p,high(p,x),offset);
}
int succ_cluster=Tree_Successor(vEB[p].summary,high(p,x));
if(succ_cluster==NIL)return NIL;
offset=Tree_Minimum(vEB[p].cluster[succ_cluster]);
return index(p,succ_cluster,offset);
}
int Tree_Predecessor(int p,int x){
if(vEB[p].u==2){
if(x==1&&vEB[p].min==0)return 0;
return NIL;
}
if(vEB[p].max!=NIL&&x>vEB[p].max)return vEB[p].max;
int offset,min_low=Tree_Minimum(vEB[p].cluster[high(p,x)]);
if(min_low!=NIL&&low(p,x)>min_low){
offset=Tree_Predecessor(vEB[p].cluster[high(p,x)],low(p,x));
return index(p,high(p,x),offset);
}
int pred_cluster=Tree_Predecessor(vEB[p].summary,high(p,x));
if(pred_cluster==NIL){
if(vEB[p].min!=NIL&&x>vEB[p].min)return vEB[p].min;
return NIL;
}
offset=Tree_Maximum(vEB[p].cluster[pred_cluster]);
return index(p,pred_cluster,offset);
}
inline void Empty_Tree_Insert(int p,int x){
vEB[p].max=vEB[p].min=x;
}
void Tree_Insert(int p,int x){
if(vEB[p].min==NIL){
Empty_Tree_Insert(p,x);
return;
}
if(x<vEB[p].min)swap(x,vEB[p].min);
if(vEB[p].u>2){
if(Tree_Minimum(vEB[p].cluster[high(p,x)])==NIL){
Tree_Insert(vEB[p].summary,high(p,x));
Empty_Tree_Insert(vEB[p].cluster[high(p,x)],low(p,x));
}else Tree_Insert(vEB[p].cluster[high(p,x)],low(p,x));
}
if(x>vEB[p].max)vEB[p].max=x;
return;
}
void Tree_Delete(int p,int x){
if(vEB[p].min==vEB[p].max){
vEB[p].min=vEB[p].max=NIL;
return;
}
if(vEB[p].u==2){
vEB[p].max=vEB[p].min=!x;
return;
}
if(x==vEB[p].min){
int first_cluster=Tree_Minimum(vEB[p].summary);
x=index(p,first_cluster,Tree_Minimum(vEB[p].cluster[first_cluster]));
vEB[p].min=x;
}
Tree_Delete(vEB[p].cluster[high(p,x)],low(p,x));
if(Tree_Minimum(vEB[p].cluster[high(p,x)])==NIL){
Tree_Delete(vEB[p].summary,high(p,x));
if(x==vEB[p].max){
int summary_max=Tree_Maximum(vEB[p].summary);
if(summary_max==NIL)vEB[p].max=vEB[p].min;
else vEB[p].max=index(p,summary_max,Tree_Maximum(vEB[p].cluster[summary_max]));
}
}else if(x==vEB[p].max)vEB[p].max=index(p,high(p,x),Tree_Maximum(vEB[p].cluster[high(p,x)]));
return;
}
int n,m,rt;
int main(){
init();
// freopen("std.in","r",stdin);
// freopen("my.out","w",stdout);
scanf("%d%d",&n,&m);
int u=0;for(--n;n;n>>=1,++u);
Tree_Build(rt,u);
while(m--){
int op,x;scanf("%d",&op);
if(op==1){
scanf("%d",&x);
if(!Tree_Member(rt,x))Tree_Insert(rt,x);
}else if(op==2){
scanf("%d",&x);
if(Tree_Member(rt,x))Tree_Delete(rt,x);
}else if(op==3){
printf("%d\n",Tree_Minimum(rt));
}else if(op==4){
printf("%d\n",Tree_Maximum(rt));
}else if(op==5){
scanf("%d",&x);
printf("%d\n",Tree_Predecessor(rt,x));
}else if(op==6){
scanf("%d",&x);
printf("%d\n",Tree_Successor(rt,x));
}else if(op==7){
scanf("%d",&x);
printf("%d\n",Tree_Member(rt,x)?1:-1);
}
}
return 0;
}
后记
终于写完啦!!1,现在是 2021 年 6 月 27 日 23 时 39 分。
写这篇文章的原因不只是因为从《算法导论》里看到的,还有一个原因是之前在日报里看到过:Ynoi的学习笔记,只是很简单的讲了一下,但也激发了我很大的兴趣。vEB 树虽然实用性不强,但是能够很好的激发思维,这才是我写完这篇文章的动力。
谢谢观看。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号