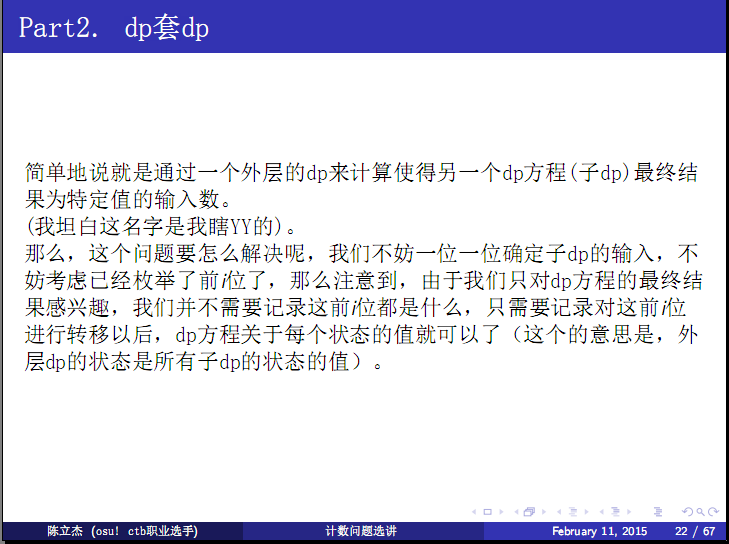
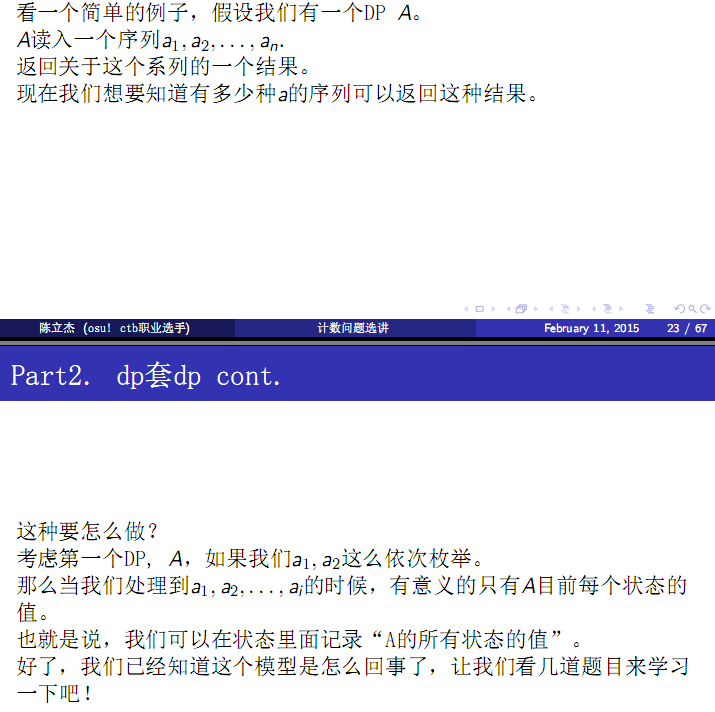
DP套DP HDOJ 4899 Hero meet devil（国王的子民的DNA）

 

题目链接

题意：

　　给n长度的S串，对于0<=i<=|S|，有多少个长度为m的T串，使得LCS(S,T) = i。

思路：

　　理解的不是很透彻，先占个坑。

#include <bits/stdc++.h>

const int S = (1 << 15) + 5;
const int MOD = 1e9 + 7;

char color[] = "ATGC";
char s[20];
int pre[20], lcs[20];
int dp[2][S], add[S][4];
int ans[20];
int n, m;

void add_mod(int &a, int b) {
    a += b;
    if (a >= MOD) {
        a -= MOD;
    }
}

int bit_count(int x) {
    return x ? bit_count (x >> 1) + (x & 1) : x;
}

void init() {
    n = strlen (s + 1);
    for (int state=0; state<(1<<n); ++state) {  //状压枚举S与T公共点的组合
        pre[0] = 0;
        for (int i=1; i<=n; ++i) {
            pre[i] = pre[i-1] + ((state>>(i-1)) & 1);  //S匹配到前i个时LCS的长度
        }
        for (int k=0; k<4; ++k) {  //T的某一个位置是color[k]，新的LCS的长度和公共点位置
            for (int i=1; i<=n; ++i) {
                if (s[i] == color[k]) {
                    lcs[i] = pre[i-1] + 1;
                } else {
                    lcs[i] = std::max (lcs[i-1], pre[i]);
                }
            }

            int &tmp = add[state][k] = 0;  //对于state状态，加一个颜色k后新的state
            for (int i=1; i<=n; ++i) {
                tmp |= ((lcs[i]!=lcs[i-1]) << (i-1));
            }
        }
    }
}

void solve() {
    int now = 0;
    memset (dp[now], 0, sizeof (dp[now]));
    dp[now][0] = 1;
    for (int i=1; i<=m; ++i) {
        now ^= 1;
        memset (dp[now], 0, sizeof (dp[now]));
        for (int state=0; state<(1<<n); ++state) {
            for (int k=0; k<4; ++k) {
                add_mod (dp[now][add[state][k]], dp[now^1][state]);
            }
        }
    }
    memset (ans, 0, sizeof (ans));
    for (int state=0; state<(1<<n); ++state) {
        add_mod (ans[bit_count (state)], dp[now][state]);
    }
    for (int i=0; i<=n; ++i) {
        printf ("%d\n", ans[i]);
    }
}

int main() {
    int T;
    scanf ("%d", &T);
    while (T--) {
        scanf ("%s", s + 1);
        scanf ("%d", &m);
        init ();
        
        solve ();
    }
    return 0;
}