「多项式乘法」

前置知识

多项式

定义

在数学中，由若干个单项式相加组成的代数式叫做多项式（若有减法：减一个数等于加上它的相反数）。多项式中的每个单项式叫做多项式的项，这些单项式中的最高项次数，就是这个多项式的次数。其中多项式中不含字母的项叫做常数项。

——百度百科

对于一个含有未知数的式子，如下：

\[y=x^2+x+3 \]

• \(x,y\) 是这个式子里的未知数，叫作元。

• \(x^2,x,3\) 是这个式子里的单项式，叫作项。

• \(^2\) 是最高项次数，叫作次数。

表示

系数表示法

即用这个多项式的每一项系数来表示这个多项式。

一个 \(n-1\) 次 \(n\) 项多项式：

\[f(x)=\sum^{n-1}_{i=0}a_ix^i \]

用系数表示法为：

\[f(x)=\{a_0,a_1...a_i...a_{n-1}\} \]

点值表示法

在初中，我们学过一次函数 \(y=kx+b\) 和二次函数 \(y=ax^2+bx+c\)，不管前面的 \(y\)，它们都是一个多项式。

我们学过：

• 给定平面直角坐标系上的两点，我们可以确定一个一次函数 \(y=kx+b\) 。

• 给定平面直角坐标系上的三点，我们可以确定一个二次函数 \(y=ax^2+bx+c\) 。

以此类推，给定平面直角坐标系上的 \(n\) 个点，我们可以确定一个 \(n-1\) 次多项式。

所以，对于一个 \(n-1\) 次多项式，我们可以用 \(n\) 个点值来表示这个多项式。

\[f(x)=\{(x_0,f(x_0)),(x_1,f(x_1))...(x_i,f(x_i))...(x_{n-1},f(x_{n-1}))\} \]

复数

定义

我们把形如 \(z=a+bi\)（\(a,b\) 均为实数）的数称为复数，其中 \(a\) 称为实部，\(b\) 称为虚部，\(i\) 称为虚数单位。当 \(z\) 的虚部等于零时，常称 \(z\) 为实数；当 \(z\) 的虚部不等于零时，实部等于零时，常称 \(z\) 为纯虚数。复数域是实数域的代数闭包，即任何复系数多项式在复数域中总有根。

复数是由意大利米兰学者卡当在十六世纪首次引入，经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作，此概念逐渐为数学家所接受。

——百度百科

在实数范围内 \(\sqrt{-1}\) 是不存在的，但是在复数中，我们定义 \(i^2=-1\) 。

也许有些难理解，不妨将一个复数看作平面直角坐标系某个一次函数上的一个点，只不过这个坐标系有些特殊，横轴是实部，纵轴是虚部。

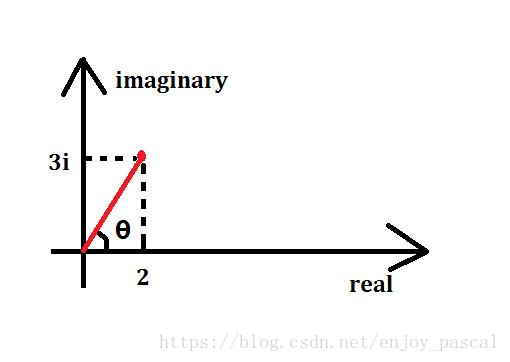
图中表示的就是一个复数 \(2 + 3i\) 。

\(PS\)：如果你把他当成向量来理解也没问题。

极角

复数在坐标系上与原点的连线和横轴所成的夹角，即上图的 \(\theta\) 。

模

复数的模就是它到坐标远点的距离：

\[|z|=\sqrt{a^2+b^2} \]

共轭复数

一个复数的共轭复数就是它虚部取反的复数：

\[\bar{z}=a-bi \]

运算

设 \(z_1=a+bi,z_2=c+di\)

加法

\[z_1+z_2=(a+c)+(b+d)i \]

复数的加法类似于向量相加，并且满足平行四边形法则：

减法

\[z_1-z_2=(a-c)+(b-d)i \]

乘法

\[z_1z_2=(a+bi)(c+di) \]

\[=ac+adi+bci+bdi^2 \]

\[=(ac-bd)+(ad+bc)i \]

性质：模长相乘，极角相加。

DFT (离散傅里叶变换)

在数学上，我们通常用于将一个 \(n\) 次多项式从系数表示法转为点值表示法。

最朴素的方法是，随便代入若干个不同的 \(x\)，用 \(\Theta (n)\) 的效率求出点值，总复杂度 \(\Theta (n^2)\) 。

如果我们代入一组特殊的 \(x\)，使 \(x\) 的若干次方都为 \(1\)，我们可以很容易计算。

但是在实数范围内，只有 \(1\) 的若干次方都为 \(1\)，是远远不够的。

但是如果我们引入复数，就会有很多数符合这个条件，傅里叶说：“下面圆上的点都能满足这个条件”。

不妨将其等分成 \(n=8\) 份，将这些点代入到多项式中。

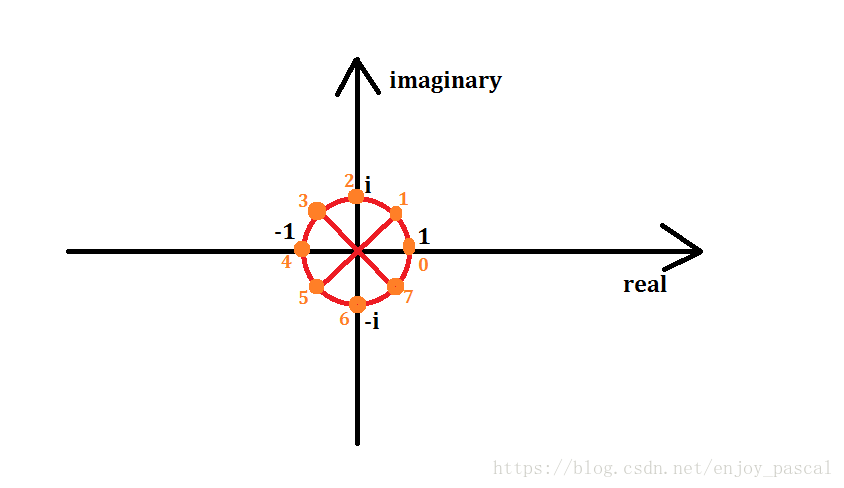
单位根

我们将上面圆上的点所代表的复数叫作单位根，用 \(w_n^k\) 表示，\(n\) 表示圆分成的份数，且通常是 \(2\) 的次幂，\(k\) 表示逆时针数第 \(k\) 个点。

\(w_n^1\) 称为 \(n\) 次单位根。

性质

• \((w_n^1)^k=w_n^k\)，由复数的乘法性质“模长相乘，极角相加”易证。

---

• \(w_n^k=cos\frac{k}{n}2\pi+isin\frac{k}{n}2\pi\)，下图易证：

---

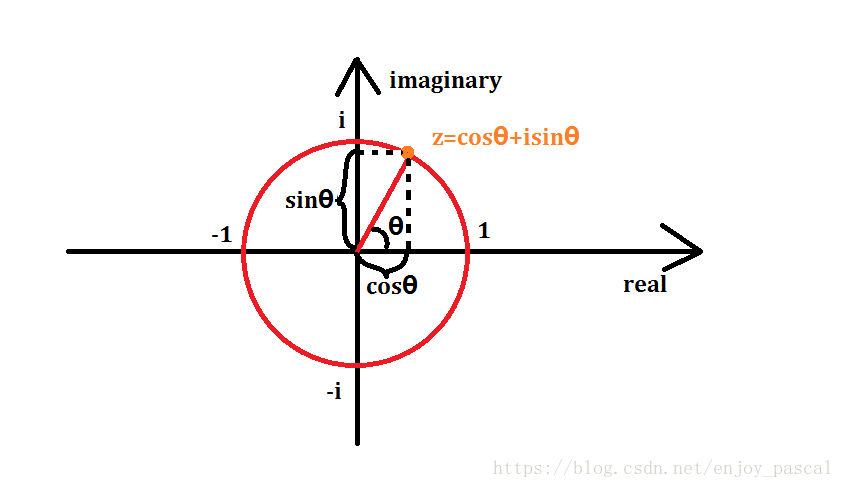
• \(w_n^k=w_{2n}^{2k}\)，证明：

\[w_n^k=cos\frac{k}{n}2\pi+isin\frac{k}{n}2\pi \]

\[=cos\frac{2k}{2n}2\pi+isin\frac{2k}{2n}2\pi \]

\[=w_{2n}^{2k} \]

---

• \(w_n^{k+\frac{2}{n}}=-w_{n}^{k}\)，证明：

\[w_n^{k+\frac{2}{n}}=w_n^kw_n^{\frac{2}{n}} \]

\[=w_n^k(cos\pi +sin\pi) \]

\[=-w_n^k \]

---

• \(w_n^0=w_n^n\)，证明：

\[w_n^0=w_n^n=1 \]

FFT (快速傅里叶变换)

我们用 \(DFT\) 计算出一些 \(w\) 值来代替 \(x\) 进行计算，但还是要暴力代入计算，复杂度还是 \(\Theta (n^2)\)...

\(FFT\) 让我们的 \(DFT\) 可以分治来做，从而使时间复杂度达到喜人的 \(\Theta(nlog^n)\) 。

设多项式

\[A(x)=\sum_{i=0}^{n-1}a_ix^i=a_0+a_1x+a_2x^2+a_3x^3...+a_{n-1}x^{n-1} \]

\[=(a_0+a_2x^2+...+a_{n-2}x^{n-2})+(a_1x+a_3x^3+...+a_{n-1}x^{n-1}) \]

\[=(a_0+a_2x^2+...+a_{n-2}x^{n-2})+x(a_1+a_3x^2+...+a_{n-1}x^{n-2}) \]

设多项式

\[A_1(x)=a_0+a_2x+a_4x^2+...+a_{n-2}x^{\frac{n-2}{2}} \]

\[A_2(x)=a_1+a_3x+a_5x^2+...+a_{n-1}x^{\frac{n-2}{2}} \]

得

\[A(x)=A_1(x^2)+xA_2(x^2) \]

设 \(k<\frac{n}{2}\) 然后将 \(w_n^k\) 作为 \(x\) 代入

\[A(w_n^k)=A_1((w_n^k)^2)+w_n^kA_2((w_n^k)^2) \]

\[=A_1(w_n^{2k})+w_n^kA_2(w_n^{2k}) \]

\[=A_1(w_\frac{n}{2}^k)+w_n^kA_2(w_\frac{n}{2}^k) \]

\[A(w_n^{k+\frac{n}{2}})=A_1(w_n^{2k+n})+w_n^{k+\frac{n}{2}}A_2(w_n^{2k+n}) \]

\[=A_1(w_n^{2k})+w_n^{k+\frac{n}{2}}A_2(w_n^{2k}) \]

\[=A_1(w_\frac{n}{2}^k)-w_n^kA_2(w_\frac{n}{2}^k) \]

证毕

所以，我们只要知道了 \(A_1(w_\frac{n}{2}^k)\) 和 \(A_2(w_\frac{n}{2}^k)\) 的值，我们就可以求 \(A(w_n^k)\) 和 \(A(w_n^{k+\frac{n}{2}})\) 的值，我们就可以分治地将多项式系数表示法转化成点值表示法。

IFFT (快速傅里叶逆变换)

我们现在已经会了将多项式系数表示法转化成点值表示法，但是怎么转化回去呢？

傅里叶告诉我们一个结论：

一个多项式在分治的过程中乘上单位根的共轭复数，分治完的每一项除以 \(n\) 即为原多项式的每一项系数。

所以我们只需 \(FFT\) 中 \(w\) 的虚部乘上 \(-1\)，并且最后将每个值除以 \(n\) 即可。

关于 FFT & IFFT 的小细节

• \(n\) 的值只能取 \(2\) 的次幂，因为我们在定义 \(w_n^k\) 时，已经限制了这个条件了。

• 当递归分治到 \(n=1\) 时，只有常数项，直接 \(return\) 。

递归 FFT 代码

inline void FFT (register int len, register Complex * a, register int opt) { // opt=1时是FFT,opt=-1时是IFFT
	if (len == 1) return; // 项数为1,只有常数项，直接返回
	register Complex a1[len >> 1], a2[len >> 1];
	for (register int i = 0; i <= len - 1; i += 2) //根据下标的奇偶分开
		a1[i >> 1] = a[i], a2[i >> 1] = a[i + 1];
	FFT (len >> 1, a1, opt), FFT (len >> 1, a2, opt); // 分治递归
	register Complex w1 = Complex (opt * sin (2.0 * pi / len), cos (2.0 * pi / len)); // w_n^1
	register Complex w = Complex (0, 1); // w_n^0
	len >>= 1;
	for (register int i = 0; i <= len - 1; i ++, w = w * w1) 
		a[i] = a1[i] + w * a2[i], a[i + len] = a1[i] - w * a2[i];
}

多项式乘法

容易发现，用系数表示法来相乘，复杂度是 \(\Theta(n^2)\) 的。

但是，转成两个点值表示法来求，复杂度是 \(\Theta(n)\) 的。

设

\[f(x)=\{(x_0,f(x_0)),(x_1,f(x_1))...(x_i,f(x_i))...(x_{n-1},f(x_{n-1}))\} \]

\[g(x)=\{(x_0,g(x_0)),(x_1,g(x_1))...(x_i,g(x_i))...(x_{n-1},g(x_{n-1}))\} \]

相乘得

\[f(x)\times g(x)=\{(x_0,f(x_0)g(x_0)),(x_1,f(x_1)g(x_1))...(x_i,f(x_i)g(x_i))...(x_{n-1},f(x_{n-1})g(x_{n-1}))\} \]

所以，我们可以用 \(FFT\) 将两个多项式转化成点值表达式，然后 \(\Theta(n)\) 相乘，再用 \(IFFT\) 转成系数表达式。

代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cmath>

using namespace std;

const int maxn = 6e6 + 50, INF = 0x3f3f3f3f;
const double pi = acos (- 1.0);

inline int read () {
	register int x = 0, w = 1;
	register char ch = getchar ();
	for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
	for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
	return x * w;
}

inline void write (register int x) {
	if (x / 10) write (x / 10);
	putchar (x % 10 + '0');
}

int n, m, len = 1;

struct Complex { // 复数，也可以用自带的complex库
	double x, y; // 虚部，实部
	Complex () { x = y = 0; }
	Complex (register double a, register double b) { x = a, y = b; }
	inline Complex operator + (const Complex &a) const { return Complex (x + a.x, y + a.y); }
	inline Complex operator - (const Complex &a) const { return Complex (x - a.x, y - a.y); }
	inline Complex operator * (const Complex &a) const { return Complex (x * a.y + y * a.x, y * a.y - x * a.x); }
} a[maxn], b[maxn];

inline void FFT (register int len, register Complex * a, register int opt) { // opt=1时是FFT,opt=-1时是IFFT
	if (len == 1) return; // 项数为1,只有常数项，直接返回
	register Complex a1[len >> 1], a2[len >> 1];
	for (register int i = 0; i <= len - 1; i += 2) //根据下标的奇偶分开
		a1[i >> 1] = a[i], a2[i >> 1] = a[i + 1];
	FFT (len >> 1, a1, opt), FFT (len >> 1, a2, opt); // 分治递归
	register Complex w1 = Complex (opt * sin (2.0 * pi / len), cos (2.0 * pi / len)); // w_n^1
	register Complex w = Complex (0, 1); // w_n^0
	len >>= 1;
	for (register int i = 0; i <= len - 1; i ++, w = w * w1) 
		a[i] = a1[i] + w * a2[i], a[i + len] = a1[i] - w * a2[i];
}

int main () {
	n = read(), m = read();
	for (register int i = 0; i <= n; i ++) a[i].y = read();
	for (register int i = 0; i <= m; i ++) b[i].y = read();
	while (len <= n + m) len <<= 1; // 项数只能是2的次幂，所以找到第一个大于n+m的即可
	FFT (len, a, 1), FFT (len, b, 1); // 系数转点值
	for (register int i = 0; i <= len - 1; i ++) a[i] = a[i] * b[i]; // 点值多项式相乘
	FFT (len, a, -1); // 点值转系数
	for (register int i = 0; i <= n + m; i ++) printf ("%d ", (int) (a[i].y / len + 0.5));
	putchar ('\n');
	return 0;
}

迭代优化

递归的效率太差了，所以我们需要一点小优化。

我们会发现，分治后的位置，是其下标二进制翻转以后的位置，我们可以先预处理好它最后到达的位置，在 \(FFT\) 之前交换即可。

迭代 FFT 代码

inline void FFT (register int len, register Complex *a, register int opt) {
	for (register int i = 1; i < len; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << bit - 1); // 预处理	
	for (register int i = 0; i < len; i ++) if (i < rev[i]) swap (a[i], a[rev[i]]); // 提前交换位置
	for (register int d = 1; d < len; d <<= 1) { // 当前变换所得序列的一半
		register Complex w1 = Complex (opt * sin (pi / d), cos (pi / d)); // 2*pi与2*d消掉了一个2
		for (register int i = 0; i < len; i += d * 2) { // 对每一段进行变换
			register Complex w = Complex (0, 1);
			for (register int j = 0; j < d; j ++, w = w * w1) {
				register Complex x = a[i + j], y = w * a[i + j + d]; // 蝴蝶变换
				a[i + j] = x + y, a[i + j + d] = x - y;
			}
		}
	}	
}

\(PS\)：网上有些三次 \(FFT\) 变两次 \(FFT\) 的做法，但是这让本来精度就不好的 \(FFT\) 更加雪上加霜，一般不怎么用，其实是我也不会。

NTT (快速数论变换)

容易发现，我们用 \(FFT\) 进行多项式乘法时引入了复数单位根，从而便于了计算，但是用的是 \(double\) 类型，精度可能会出问题，或许我们能找到某个东西来代替单位根。

阶

设 \(a,p\) 是整数，\(a\) 和 \(p\) 互质，那么：

使 \(a^n\equiv 1\mod p\) 成立的最小正整数 \(n\) 叫做 \(a\) 模 \(p\) 的阶，记作 \(\delta_p(a)=n\) 。

——百度百科

例如：

\[\delta_7(2)=3 \]

\[2^3\equiv 1\mod 7 \]

原根

设 \(m\) 是正整数，\(a\) 是整数，若 \(a\) 模 \(m\) 的阶等于 \(\phi (m)\)，则称 \(a\) 为模 \(m\) 的一个原根。

——百度百科

具体原根性质详见百度百科，这里我们只用到了基本定义。

对于一个模数 \(p\)，设它的原根为 \(g\)，则有：

\[g^{\phi (p)}\equiv 1\mod p \]

若 \(p\) 为质数，则有：

\[\phi (p) = p - 1 \]

\[g^{p-1}\equiv 1\mod p \]

根据单位根的性质，有：

\[(\omega_n^1)^n=g^{p-1}\equiv 1\mod p \]

\[\omega_n^1=g^{\frac{p-1}{n}} \]

\[\omega_n^{-1}=g^{-\frac{p-1}{n}} \]

这样我们就能够用原根来代替单位根了。

NTT 代码

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

typedef long long ll;

using namespace std;

const int maxn = 3e6 + 50, INF = 0x3f3f3f3f, mod = 998244353;

inline int read () {
	register int x = 0, w = 1;
	register char ch = getchar ();
	for (; ch < '0' || ch > '9'; ch = getchar ()) if (ch == '-') w = -1;
	for (; ch >= '0' && ch <= '9'; ch = getchar ()) x = x * 10 + ch - '0';
	return x * w;
}

inline void write (register int x) {
	if (x / 10) write (x / 10);
	putchar (x % 10 + '0');
}

int n, m, len = 1, bit, rev[maxn];
ll a[maxn], b[maxn];

inline ll qpow (register ll a, register ll b) {
	register ll ans = 1;
	while (b) {
		if (b & 1) ans = ans * a % mod;
		a = a * a % mod, b >>= 1;
	}
	return ans;
}

inline void NTT (register int len, register ll * a, register ll opt) {
	for (register int i = 1; i <= len; i ++) if (i < rev[i]) swap (a[i], a[rev[i]]);
	for (register int d = 1; d < len; d <<= 1) {
		register ll w1 = qpow (opt, (mod - 1) / (d << 1));
		for (register int i = 0; i < len; i += d << 1) {
			register ll w = 1;
			for (register int j = 0; j < d; j ++, w = w * w1 % mod) {
				register ll x = a[i + j], y = w * a[i + j + d] % mod;
				a[i + j] = (x + y) % mod, a[i + j + d] = (x - y + mod) % mod;
			}
		}
	}
}

int main () {
	n = read(), m = read();
	while (len <= n + m) len <<= 1, bit ++;
	for (register int i = 0; i <= n; i ++) a[i] = read();
	for (register int i = 0; i <= m; i ++) b[i] = read();
	for (register int i = 1; i <= len; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << bit - 1);
	NTT (len, a, 3), NTT (len, b, 3);
	for (register int i = 0; i <= len; i ++) a[i] = a[i] * b[i] % mod;
	NTT (len, a, qpow (3, mod - 2));
	for (register int i = 0; i <= n + m; i ++) printf ("%lld ", a[i] * qpow (len, mod - 2) % mod); putchar ('\n');
	return 0;
}