「NOI 2020」美食家

「NOI 2020」美食家

题面

某谷P6772

基本思路

从 \(n \leq 50\) 和 \(w \leq 5\) 中不难看出，这是一个矩阵快速幂，利用一个拆点的思想，可以先做一下 P4159迷路，然后再用一个二进制拆分，不错，就是 P6190魔法。

将上俩个题的思路综合起来，这个题就好处理多了。

拆点

何为拆点，如何拆点？

首先，我们拿一个图为例：

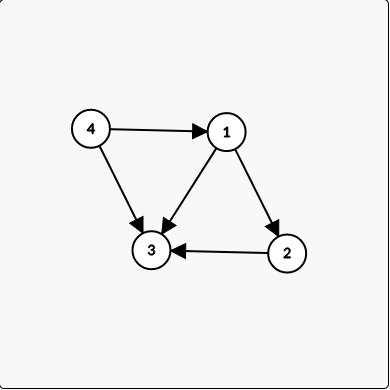
当前这个图的01邻接矩阵为：

\(\begin{bmatrix} 0&1&1&0 \\ 0&0&1&0 \\ 0&0&0&0 \\ 1&0&1&0 \end{bmatrix}\)

可以理解为 \(a[i][j]\) 从 \(i\) 走一步能否到 \(j\) 。

将这个矩阵相乘：

\( \begin{bmatrix} 0&1&1&0 \\ 0&0&1&0 \\ 0&0&0&0 \\ 1&0&1&0 \\ \end{bmatrix} \times \begin{bmatrix} 0&1&1&0 \\ 0&0&1&0 \\ 0&0&0&0 \\ 1&0&1&0 \end{bmatrix} = \begin{bmatrix} 0&0&1&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&1&1&0 \end{bmatrix} \)

易证，得出的矩阵 \(a[i][j]\) 表示从 \(i\) 走 \(2\) 步能否到达 \(j\) 。

不妨设一开始的矩阵为 \(base\) ，则可以得出：\(base^k\) 为从 \(i\) 走 \(k\) 步能否到达 \(j\) 。

---

但是这道题还有一个点权，该怎么统计呢？

我们可以将矩阵中的元素更改，并将矩阵乘法的运算重新定义。

不妨设 \(a[i][j]\) 为从 \(i\) 到 \(j\) 的最长路，那么矩阵中的运算就改为了：

c.a[i][j] = max (c.a[i][j], a.a[i][k] + b.a[k][j]);

注意将不能到达的点，权值设为 \(-INF\)，这样无论怎样相加都不会影响到答案了。

---

emmmm，好像跑的有点远。

由于我们的矩阵只支持边权为1时的图，所以我们要拆点。

拆点，顾名思义，就是将一个点拆成多个点，如下图：

图中1、6 ,就是我们原来的1和2 。

如果我们要从2到1建一条边权为3的边，我们就将新图中从6到3建一条边，这样就达到了我们的目的，也可以跑矩阵快速幂了。

分块快速幂

如果 \(k=0\)，那么答案很简单就是 \(base^T.a[1][1]\) 。

若 \(k\neq0\)，我们可以将整段 \(T\) 时间分成 \(k+1\) 块进行矩阵快速幂。

这样在每次美食节结束的时候，在统计答案的矩阵里，在相应的位置加上额外的贡献即可。

到现在我们就可以粗略的码一个效率为 \(\Theta(kn^3log_T)\) 的小暴力，显然会T到飞起。

二进制拆分

从上面我们会发现，在每次分块快速幂的时候，我们都将统计答案的 \(ans\) 矩阵乘上了一个 \(base^t\)。

我们可以现将 \(base\) 矩阵的 \(2^x\) 次方预处理出来。

在统计答案时，将这段时间二进制拆分，乘上相应的 \(base^{2^x}\)。

好像差不多可以优化一个 \(log\) 的效率，但还是会T到飞起。

搞掉一个n

怎么能搞掉一个n呢？

我们会发现，我们统计答案的矩阵 \(ans\)，只用到了 \(i = 1\) 的地方，所以我们直接只计算 \(i = 1\) 的那一行的答案即可。

搞掉一个n不轻轻松松？

当前复杂度 \(\Theta(kn^2logT)\)，直接碾掉！！！

代码（自带大常数）

#include <cstdio>
#include <cstring>
#include <algorithm>

#define ll long long
#define DEBUG puts ("emmmm")

using namespace std;

const int maxn = 5e2 + 50;

inline int read () {
	int x = 0, w = 1;
	char ch = getchar();
	for (; ch < '0' || ch > '9'; ch = getchar()) if (ch == '-') w = -1;
	for (; ch >= '0' && ch <= '9'; ch = getchar()) x = x * 10 + ch - '0';
	return x * w;
}

int n, m, T, K;
int c[maxn];

struct Festival{
	int t, pos, val;
	inline bool operator < (const Festival &a) const {
		return t < a.t;
	};
}Fes[maxn];

struct Matrix{
	ll a[260][260];
	Matrix () {
		memset (a, -0x3f, sizeof a); //初始为-INF，对答案不会造成影响
	};
}base, ans, basem[50];

inline Matrix Matx (Matrix a, Matrix b) {
	Matrix ans;
	register int i = 1, j = 1, k = 1;
	for (; i <= n * 5; i ++) {
		for (j = 1; j <= n * 5; j ++) {
			for (k = 1; k <= n * 5; k ++) {
				ans.a[i][j] = max (ans.a[i][j], a.a[i][k] + b.a[k][j]);
			}
		}
	}
	return ans;
}

inline Matrix Matx0 (Matrix a, Matrix b) {
	Matrix ans;
	register int j = 1, k = 1;
	for (; j <= n * 5; j ++) {
		for (k = 1; k <= n * 5; k ++) {
			if (a.a[1][k] != -1 && b.a[k][j] != -1) ans.a[1][j] = max (ans.a[1][j], a.a[1][k] + b.a[k][j]);
		}
	}
	return ans;
}

inline Matrix Matqpow (Matrix a, register int b) {
	Matrix ans;
	register int i = 1;
	for (; i <= n * 5; i ++) ans.a[i][i] = 1;
	while (b) {
		if (b & 1) ans = Matx (ans, a);
		a = Matx (a, a);
		b >>= 1;
	}
	return ans;
}

int main () {
	freopen ("delicacy.in", "r", stdin);
	freopen ("delicacy.out", "w", stdout);
	n = read(), m = read(), T = read(), K = read();
	for (register int i = 1; i <= n; i ++) c[i] = read();
	for (register int i = 1; i <= n; i ++) {
		for (register int j = 1; j <= 4; j ++) {
			register int u = (i - 1) * 5 + j + 1, v = (i - 1) * 5 + j; // 负责的建边，建议自己模拟
			if (j != 1) base.a[u][v] = 0;
			else base.a[u][v] = c[i];
		}
	}
	for (register int i = 1; i <= m; i ++) {
		register int u = read(), v = read(), w = read();
		if (w != 1) base.a[(u - 1) * 5 + 1][(v - 1) * 5 + w] = 0; // 负责的建边，建议自己模拟
		else base.a[(u - 1) * 5 + 1][(v - 1) * 5 + w] = c[v];
	}
	for (register int i = 1; i <= K; i ++) Fes[i].t = read(), Fes[i].pos = read(), Fes[i].val = read();
	sort (Fes + 1, Fes + K + 1);
	Fes[++ K].t = T;
	basem[1] = base;
	for (register int i = 2; (1 << i - 1) <= T; i ++) {
		basem[i] = Matx (basem[i - 1], basem[i - 1]);
	}
	register int last = 0;
	register bool flag = 0;
	ans.a[1][1] = 0;
	for (register int i = 1; i <= K; i ++) {
		register int x = Fes[i].t - last;
		for (register int j = 1; j <= 30; j ++) {
			if (1 << j - 1 & x) {
				ans = Matx0 (ans, basem[j]);
			}
		}
		last = Fes[i].t;
		for (register int j = 1; j <= n * 5; j ++) {
			if (ans.a[j][(Fes[i].pos - 1) * 5 + 1] >= 0) {
				ans.a[j][(Fes[i].pos - 1) * 5 + 1] += Fes[i].val;	
			}
		}
	}
	if (ans.a[1][1] < 0) {
		puts ("-1");
	}else {
		printf ("%lld\n", ans.a[1][1] + c[1]); // 别忘了最后加上刚开始获得的愉悦值
	}
	return 0;
}