大假期集训模拟赛13
斐波那契(fibonacci)
题目描述
小 \(C\) 养了一些很可爱的兔子。
有一天,小 \(C\) 突然发现兔子们都是严格按照伟大的数学家斐波那契提出的模型来进行繁衍:
一对兔子从出生后第二个月起,每个月刚开始的时候都会产下一对小兔子。我们假定,在整个过程中兔子不会出现任何意外。
小 \(C\) 把兔子按出生顺序,把兔子们从 \(1\) 开始标号,并且小 \(C\) 的兔子都是 \(1\) 号兔子和 \(1\) 号兔子的后代。如果某两对兔子是同时出生的,那么小 \(C\) 会将父母标号更小的一对优先标号。
如果我们把这种关系用图画下来,前六个月大概就是这样的:
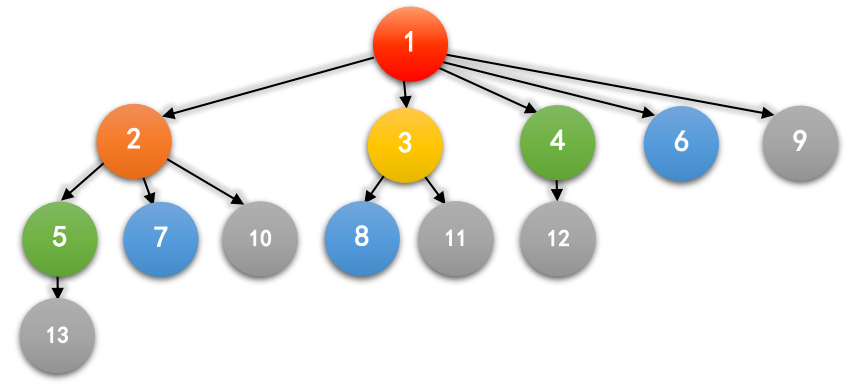
其中,一个箭头 \(A→B\) 表示 \(A\) 是 \(B\) 的祖先,相同的颜色表示同一个月出生的兔子。
为了更细致地了解兔子们是如何繁衍的,小 \(C\) 找来了一些兔子,并且向你提出了 \(m\) 个问题:她想知道关于每两对兔子 \(a_i\) 和 \(b_i\) ,他们的最近公共祖先是谁。你能帮帮小 \(C\) 吗?
一对兔子的祖先是这对兔子以及他们父母(如果有的话)的祖先,而最近公共祖先是指两对兔子所共有的祖先中,离他们的距离之和最近的一对兔子。比如, \(5\) 和 \(7\) 的最近公共祖先是 \(2\), \(1\) 和 \(2\) 的最近公共祖先是 \(1\) , \(6\) 和 \(6\) 的最近公共祖先是 \(6\) 。
输入格式
输入第一行,包含一个正整数 \(m\) 。
输入接下来 \(m\) 行,每行包含 \(2\) 个正整数,表示 \(a_i\) 和 \(b_i\) 。
输出格式
输入一共 \(m\) 行,每行一个正整数,依次表示你对问题的答案。
样例
样例输入
5
1 1
2 3
5 7
7 13
4 12
样例输出
1
1
2
2
4
数据范围与提示
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表:
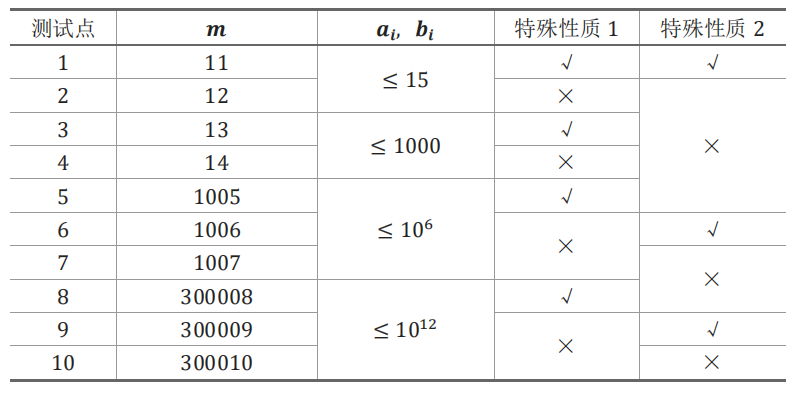
特殊性质 \(1\):保证 \(a_i,b_i\) 均为某一个月出生的兔子中标号最大的一对兔子。例如,对于前六个月,标号最大的兔子分别是 \(1, 2, 3, 5, 8, 13\) 。
特殊性质 \(2\):保证 \(|a_i-b_i|\leq 1\) 。
思路
其实就是找个规律,根本用不到建图求 \(LCA\) ,而且数据范围太大,也存不下,但是数据很水,能够混上 \(80opts\) 。
思路跟求 \(LCA\) 差不多,当我们仔细思考特殊我们会发现:
当 \(|a_i-b_i|=1\) 时,他们的 \(LCA\) 只会是 \(1\) 。
当 \(a_i,b_i\) 为标号最大的兔子时,他的父亲会是 \(fib[x-2]\) 。
剩下的情况,二分查找一下小于这个值的最大 \(fibonacci\) 值,减去这个值,就可以得到他的父亲。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+50,INF=0x3f3f3f3f,mod=1e9+7;
inline int read(){
int x=0,w=1;
char ch;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
int fib[66]={1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,75025,121393,196418,317811,514229,832040,1346269,2178309,3524578,5702887,9227465,14930352,24157817,39088169,63245986,102334155,165580141,267914296,433494437,701408733,1134903170,1836311903,2971215073,4807526976,7778742049,12586269025,20365011074,32951280099,53316291173,86267571272,139583862445,225851433717,365435296162,591286729879,956722026041,1548008755920};
int m;
int Dic(int x){//二分查找
int l=0,r=60;
while(l<=r){
int mid=(l+r)>>1;
if(fib[mid]>x){
r=mid-1;
}else if(fib[mid]<x){
l=mid+1;
}else if(fib[mid]==x){
return mid;
}
}
return l-1;
}
signed main(){
m=read();
while(m--){
int a=read(),b=read();
int f1=a,f2=b;
while(1){
if(f1==f2){//找到了LCA
printf("%lld\n",f1);
break;
}
if(abs(f1-f2)==1){//特殊性质2
printf("1\n");
break;
}
if(f1<f2)swap(f1,f2);//优先更新深度比较深的点
int x=Dic(f1);
if(f1==fib[x]) f1=fib[x-2];
if(f1>fib[x]) f1-=fib[x];
}
}
return 0;
}
数颜色
题目描述
小 \(C\) 的兔子不是雪白的,而是五彩缤纷的。每只兔子都有一种颜色,不同的兔子可能有相同的颜色。小 \(C\) 把她标号从 \(1\) 到 \(n\) 的 \(n\) 只兔子排成长长的一排,来给他们喂胡萝卜吃。排列完成后,第 \(i\) 只兔子的颜色是 \(a_i\) 。
俗话说得好,"萝卜青菜,各有所爱"。小 \(C\) 发现,不同颜色的兔子可能有对胡萝卜的不同偏好。比如,银色的兔子最喜欢吃金色的胡萝卜,金色的兔子更喜欢吃胡萝卜叶子,而绿色的兔子却喜欢吃酸一点的胡萝卜……为了满足兔子们的要求,小 \(C\) 十分苦恼。所以,为了使得胡萝卜喂得更加准确,小 \(C\) 想知道在区间 \([l_j,r_j]\) 里有多少只颜色为 \(c_j\) 的兔子。
不过,因为小 \(C\) 的兔子们都十分地活跃,它们不是很愿意待在一个固定的位置;与此同时,小 \(C\) 也在根据她知道的信息来给兔子们调整位置。所以,有时编号为 \(x_j\) 和 \(x_{j+1}\) 的两只兔子会交换位置。
小 \(C\) 被这一系列麻烦事给难住了。你能帮帮她吗?
输入格式
输入第 \(1\) 行两个正整数 \(n,m\) 。
输入第 \(2\) 行 \(n\) 个正整数,第 \(i\) 个数表示第 \(i\) 只兔子的颜色 \(a_i\) 。
输入接下来 \(m\) 行,每行为以下两种中的一种:
- \(1,l_j,r_j,c_j\) :询问在区间 \([l_j,r_j]\) 里有多少只颜色为 \(c_j\) 的兔子;
- \(2,x_j\) :\(x_j\) 和 \(x_{j+1}\) 两只兔子交换了位置
输出格式
对于每个 \(1\) 操作,输出一行一个正整数,表示你对于这个询问的答案
样例
样例输入
6 5
1 2 3 2 3 3
1 1 3 2
1 4 6 3
2 3
1 1 3 2
1 4 6 3
样例输出
1
2
2
3
样例说明
前两个 \(1\) 操作和后两个 \(1\) 操作对应相同;在第三次的 \(2\) 操作后,\(3\) 号兔子和 \(4\) 号兔子交换了位置,序列变为 \(1 \:\ 2 \:\ 2 \:\ 3 \:\ 3 \:\ 3\) 。
数据范围与提示
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解决一部分测试数据。
对于所有测试点,有 \(1\leq l_j\leq r_j\leq n,1\leq x_j\leq n\) 。
每个测试点的数据规模及特点如下表:
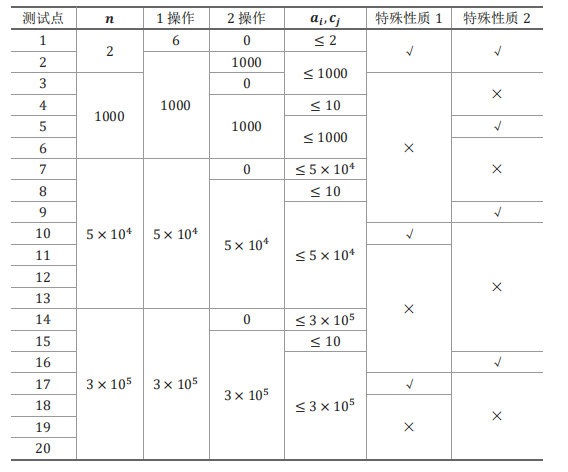
特殊性质 \(1\) :保证对于所有操作 \(1\),有 \(|r_j-l_j|\leq 20\) 或 \(|r_j-l_j|\geq n-20\) 。
特殊性质 \(2\) :保证不会有两只兔子相同颜色的兔子。
思路
这个题就不用跟 \(T1\) 一样,去按着特殊性质去找规律了。
听说这个题卡高级数据结构,幸好我不会。
这个题就看你用 \(STL\) 用的熟不熟练了,虽然很多函数名我也没记住,也是一个一个试的。
打了一手 \(vector\) ,糊掉了,没有将原数组进行交换,直接爆炸。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn=3e5+50,INF=0x3f3f3f3f;
inline int read(){
int x=0,w=1;
char ch;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
int n,m;
int a[maxn],size[maxn];
vector<int> vec[maxn];
int main(){
n=read(),m=read();
for(int i=1;i<=n;i++){
a[i]=read();
size[a[i]]++;
vec[a[i]].push_back(i);
}
while(m--){
int opt=read();
if(opt==1){
int l=read(),r=read(),c=read();
int x=lower_bound(vec[c].begin(),vec[c].begin()+size[c],l)-vec[c].begin();//找到左端点
int y=lower_bound(vec[c].begin(),vec[c].begin()+size[c],r+1)-vec[c].begin();//找到右端点
printf("%d\n",max(y-x,0));
}else if(opt==2){
int w=read();
if(a[w]==a[w+1])continue;//不知道有没有用的剪枝
int x=lower_bound(vec[a[w]].begin(),vec[a[w]].begin()+size[a[w]],w)-vec[a[w]].begin();
vec[a[w]][x]=w+1;
int y=lower_bound(vec[a[w+1]].begin(),vec[a[w+1]].begin()+size[a[w+1]],w+1)-vec[a[w+1]].begin();
vec[a[w+1]][y]=w;
swap(a[w],a[w+1]);//千万记得
}
}
return 0;
}
矩阵游戏
题目描述
\(LZK\) 发明一个矩阵游戏,大家一起来玩玩吧,有一个 \(N\) 行 \(M\) 列的矩阵。第一行的数字是 \(1,2,...M\) ,第二行的数字是 \(M+1,M+2,...2\times M\) ,以此类推,第 \(N\) 行的数字是 \((N-1)\times M+1,(N-1)\times M+2,...N\times M\) 。
例如, \(N=3,M=4\) 的矩阵是这样的:
1 2 3 4
5 6 7 8
9 10 11 12
对于身为智慧之神的 \(LZK\) 来说,这个矩阵过于无趣.于是他决定改造这个矩阵,改造会进行 \(K\) 次,每次改造会将矩阵的某一行或某一列乘上一个数字,你的任务是计算最终这个矩阵内所有数字的和,输出答案对 \(10^9+7\) 取模。
输入格式
第一行包含三个正整数 \(N\)、\(M\)、\(K\),表示矩阵的大小与改造次数。接下来的行,每行会是如下两种形式之一:
- \(R,X,Y\) ,表示将矩阵的第 \(X(1\leq X\leq N)\) 行变为原来的 \(Y(0\leq Y\leq 10^9)\) 倍.
- \(S,X,Y\) ,表示将矩阵的第 \(X(1\leq X\leq M)\) 列变为原来的 \(Y(0\leq Y\leq 10^9)\) 倍.
输出格式
输出一行一个整数,表示最终矩阵内所有元素的和对 \(10^9+7\) 取模的结果。
样例
样例输入输出 #1
game.in
3 4 4
R 2 4
S 4 1
R 3 2
R 2 0
game.out
94
样例输入输出 #2
game.in
2 4 4
S 2 0
S 2 3
R 1 5
S 1 3
game.out
80
数据范围与提示
\(40\%\) 的数据满足: \(1\leq N,M\leq 1000\);
\(80\%\) 的数据满足: \(1\leq N,M\leq 1000000,1\leq K\leq 1000\);
\(100\%\) 的数据满足: \(1\leq N,M\leq 1000000,1\leq K\leq 100000\) 。
思路
- \(40opts\) 的分段
很简单,直接在线改变就行了,不过别忘了开 \(long long\) ,每次乘也要取模,不然直接爆零。
- \(100opts\) 的正解
我们会发现,先进行行的乘法和先进行列的乘法,结果是一样的,而且每次更新的先后顺序改变,也不会对结果造成影响。
所以我们预先统计一下每一行的所有要成上的乘数的积(注意取模)。
\(Row[i]\) 表示第 \(i\) 行所有乘数的积,\(Col[j]\) 表示第 \(j\) 列所以乘数的积。
我们先进行行的乘法,统计每一列 \(sum_j\) 在进行行的乘法后的总和。
\(sum_j=\sum _{i=1}^{n} Row[i]\times [(i-1)\times m+j]\)
\(sum_j=\sum _{i=1}^{n} Row[i]\times (i-1)\times m+\sum _{i=1}^{n} Row[i]\times j\)
设 \(k_1=\sum _{i=1}^{n} Row[i]\times (i-1)\times m,k2=\sum _{i=1}^{n} Row[i]\times j\)
这样我们就可以用 \(O_n\) 的效率预处理出 \(k_1\) 和 \(\sum _{i=1}^{n} Row[i]\),最后枚举一遍 \(j\) ,加和求值即可。(注意取模)
其实我们观察可以发现,每一行每一列,都是一个等差数列,而且每一列的和也是个等差数列,所以我们在进行乘法的时候,我们只将首项和公差改变即可,最后求和就行。
代码
法一
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e6+50,INF=0x3f3f3f3f,mod=1e9+7;
inline int read(){
int x=0,w=1;
char ch;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
int n,m,k;
int Row[maxn],Col[maxn];
void Init(){
for(int i=1;i<=n;i++) Row[i]=1;//初始为1,不然全是0了
for(int i=1;i<=m;i++) Col[i]=1;
}
signed main(){
n=read(),m=read(),k=read();
Init();
for(int i=1;i<=k;i++){
char opt;
cin>>opt;
int x=read(),y=read();
if(opt=='R'){//记录每行乘的值
Row[x]=(Row[x]*y)%mod;
}else if(opt=='S'){//记录每列乘的值
Col[x]=(Col[x]*y)%mod;
}
}
int k1=0,k2=0;
for(int i=1;i<=n;i++){//套用公式
k1=(k1+Row[i]*(i-1)%mod*m%mod)%mod;
}
for(int i=1;i<=n;i++){
k2=(k2+Row[i])%mod;
}
int ans=0;
for(int j=1;j<=m;j++){
ans=(ans+(k1+j*k2)%mod*Col[j]%mod)%mod;
}
printf("%lld\n",ans);
return 0;
}
法二(借用老姚代码)
#include <bits/stdc++.h>
typedef long long LL;
const int maxn=1e6+5;
const LL Mod=1e9+7;
LL col[maxn];//col[i]记录第i列的乘数
LL a[maxn],b[maxn];//a[i],b[i]分别为第i行首项和公差
LL sum[maxn];//sum[i]表示第i列之和
int n,m;
void Init(){
int k;scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;++i){
a[i]=(1LL*(i-1)*m+1)%Mod;//第i行的首项
b[i]=1;//第i行的公差
}
for(int i=1;i<=m;++i)col[i]=1;
while(k--){
LL x,y;char ch;
scanf(" %c%lld%lld",&ch,&x,&y);
if(ch=='S')
col[x]=(col[x]*y)%Mod;
if(ch=='R'){
a[x]=(a[x]*y)%Mod;
b[x]=(b[x]*y)%Mod;
}
}
}
void Solve(){
LL d=0,ans=0;
for(int i=1;i<=n;++i){//求出第一列之和
sum[1]=(sum[1]+a[i])%Mod;//首项
d=(d+b[i])%Mod;//公差
}
for(int i=2;i<=m;++i)//利用等差数列公式求出其他列之和
sum[i]=(sum[i-1]+d)%Mod;
for(int i=1;i<=m;++i)
ans=(ans+sum[i]*col[i]%Mod)%Mod;
printf("%lld\n",ans);
}
int main(){
Init();
Solve();
return 0;
}
优美序列
题目描述
\(Lxy\) 养了 \(N\) 头奶牛,他把 \(N\) 头奶牛用 \(1...N\) 编号,第 \(i\) 头奶牛编号为 \(i\) 。
为了让奶牛多产奶,每天早上他都会让奶牛们排成一排做早操。奶牛们是随机排列的。
在奶牛排列中,如果一段区间 \([L,R]\) 中的数从小到大排列后是连续的,他认为这段区间是优美的。比如奶牛排列为: \((3,1,7,5,6,4,2)\),区间 \([3,6]\) 是优美的,它包含 \(4,5,6,7\) 连续的四个数,而区间 \([1,3]\) 是不优美的。
\(Lxy\) 的问题是:对于给定的一个区间 \([L,R](1\leq L\leq R\leq N)\) , 他想知道,包含区间 \([L,R]\) 的最短优美区间,比如区间 \([1,3]\) 的最短优美区间是 \([1,7]\) 。
输入格式
第一行为一个整数 \(N\) ,表示奶牛的个数。
第二行为 \(1\) 到 \(N\) 的一个排列,表示奶牛的队伍。
第三行为一个整数 \(M\) ,表示有 \(M\) 个询问。
后面有 \(M\) 行,每行有两个整数 \(L,R\) 表示询问区间。
输出格式
输出为 \(M\) 行,每行两个整数,表示包含询问区间的最短优美区间。
样例
样例输入
7
3 1 7 5 6 4 2
3
3 6
7 7
1 3
样例输出
3 6
7 7
1 7
数据范围与提示
\(15\%\) 的数据满足: \(1\leq N,M\leq 15\);
\(50\%\) 的数据满足: \(1\leq N,M\leq 1000\);
\(100\%\) 的数据满足: \(1\leq N,M\leq 100000\) 。
思路
析合树的应用,本人还没看明白,待更新~~~~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号