大假期集训模拟赛12
折纸
题目描述
小 \(s\) 很喜欢折纸。
有一天,他得到了一条很长的纸带,他把它从左向右均匀划分为 \(N\) 个单位长度,并且在每份的边界处分别标上数字 \(0\sim n\) 。
然后小 \(s\) 开始无聊的折纸,每次他都会选择一个数字,把纸带沿这个数字当前所在的位置翻折(假如已经在边界上了那就相当于什么都不做)。
小 \(s\) 想知道 \(M\) 次翻折之后纸带还有多长。
输入格式
输入包含多组数据,第一为一个正整数 \(T,0<T\leq 10\) 。
接下来,每组数据包括两行。
第一行包含两个正整数 \(N\) 和 \(M\) ,表示纸带的长度和操作的次数。
第二行包含 \(M\) 个整数 \(D_i\) ,其中 \(D_i\) 表示第 \(i\) 次选择的数字。
输出格式
每组数据输出一行,只有一个数字,即纸带最后的长度。
样例
样例输入
2
5 2
3 5
5 2
3 2
样例输出
2
2
数据范围与提示
\(100\%\) 的数据中 \(N\leq 10^{18},M\leq 3000\) 。
思路
很简单的一个模拟,考试的时候想复杂了,而且只是往同一个方向翻折。
其实思路很简单,我们会发现当我们进行第 \(i\) 次翻折的时候,只有前面的翻折会对这次翻折造成影响,所以我们只需要记录每次翻折的折点,在遍历前 \(j(1\leq j<i)\) 次翻折,改变第 \(i\) 次翻折的折点即可。
我们可以通过 \(f[i]\) 来记录第 \(i\) 次翻折的时候,是向左翻的还是向右翻的,再以 \(a[j]\) 为对称点,改变 \(a[i]\) 的值即可。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=1e5+50,INF=0x3f3f3f3f;
inline int read(){
int x=0,w=1;
char ch;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
int T;
int n,m;
int a[maxn],f[maxn];
signed main(){
T=read();
while(T--){
n=read(),m=read();
int head=0,tail=n;//记录当前纸条的首尾
for(int i=1;i<=m;i++){
int x=read();
if(x==head||x==tail)continue;//在边界直接跳过
for(int j=1;j<=i-1;j++){//改变x的值
if(a[j]<x&&f[j]==2){
x=2*a[j]-x;
}else if(a[j]>x&&f[j]==1){
x=2*a[j]-x;
}
}
if(x-head<tail-x){//从左往右翻
head=x;
f[i]=1;
}else{//从右往左翻
tail=x;
f[i]=2;
}
a[i]=x;
}
printf("%lld\n",tail-head);
}
return 0;
}
water
题目描述
有一块矩形土地被划分成 \(n\times m\) 个正方形小块。这些小块高低不平,每一小块都有自己的高度。水流可以由任意一块地流向周围四个方向的四块地中,但是不能直接流入对角相连的小块中。
一场大雨后,由于地势高低不同,许多地方都积存了不少降水。给定每个小块的高度,求每个小块的积水高度。
注意:假设矩形地外围无限大且高度为 \(0\) 。
输入格式
第一行包含两个非负整数 \(n,m\) 。
接下来 \(n\) 行每行 \(m\) 个整数表示第 \(i\) 行第 \(j\) 列的小块的高度。
输出格式
输出 \(n\) 行,每行 \(m\) 个由空格隔开的非负整数,表示每个小块的积水高度。
样例
样例输入
3 3
4 4 0
2 1 3
3 3 -1
样例输出
0 0 0
0 1 0
0 0 1
数据范围与提示
对于 \(20\%\) 的数据 \(n,m\leq 4\) 。
对于 \(40\%\) 的数据 \(n,m\leq 15\) 。
对于 \(60\%\) 的数据 \(n,m\leq 50\) 。
对于 \(100\%\) 的数据 \(n,m\leq 300\) ,|小块高度| \(\leq 10^9\) 。
在每一部分数据中,均有一半数据保证小块高度非负
思路
前几天考了好几次这种题型,将棋盘式的图转化成一个一维的图论来处理。
我们会发现:当一个块儿的四周有比它高度小或跟它高度相同的块儿时,它就存不住水了。
我们可以向四周建边,边权为两个块儿的最大高度,在做一遍最小生成树,深搜一遍求解即可。
代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=300+50,INF=0x3f3f3f3f;
inline int read(){
int x=0,w=1;
char ch;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
int n,m;
int pan[maxn][maxn];
int dx[4]={1,0,-1,0};
int dy[4]={0,-1,0,1};
int f[maxn*maxn];
int cnt;
struct Edge{
int from,to,w;
}e[maxn*maxn*10];
struct EDGE{
int to,next,w;
}g[maxn*maxn*10];
int tot,head[maxn*maxn<<2];
void Add(int u,int v,int w){
g[++tot].to=v;
g[tot].w=w;
g[tot].next=head[u];
head[u]=tot;
}
bool cmp(Edge a,Edge b){
return a.w<b.w;
}
int Find(int x){
return f[x]==x ? x : f[x]=Find(f[x]);
}
void Merge(int x,int y){
f[Find(x)]=Find(y);
}
void Kurscal(){//最小生成树
for(int i=1;i<=cnt;i++){
int u=e[i].from,v=e[i].to,w=e[i].w;
if(Find(u)!=Find(v)){
Merge(u,v);
Add(u,v,w);//双向边
Add(v,u,w);
}
}
}
void DFS(int u,int fa,int maxx){
for(int i=head[u];i;i=g[i].next){
int v=g[i].to;
if(v==fa)continue;
int vx=v/m+1,vy=v%m;//求出坐标值
if(vy==0){
vx--;
vy=m;
}
pan[vx][vy]=max(maxx,g[i].w)-pan[vx][vy];//求出积水量
DFS(v,u,max(maxx,g[i].w));
}
}
signed main(){
n=read(),m=read();
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
pan[i][j]=read();
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int k=0;k<=3;k++){
int xx=i+dx[k],yy=j+dy[k];
int x=(i-1)*m+j,y=(xx-1)*m+yy;
if(xx==0||yy==0||yy>m||xx>n){
y=0;
}
if(i==0||j==0||i>n||j>m){
x=0;
}
if(x==0&&y==0)continue;
e[++cnt].from=x;//双向边
e[cnt].to=y;
e[cnt].w=max(pan[i][j],pan[xx][yy]);
e[++cnt].from=y;
e[cnt].to=x;
e[cnt].w=max(pan[i][j],pan[xx][yy]);
}
}
}
for(int i=1;i<=n*m;i++){
f[i]=i;
}
sort(e+1,e+cnt+1,cmp);
Kurscal();
DFS(0,-1,-INF);
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
printf("%lld ",pan[i][j]);
}
printf("\n");
}
printf("\n");
return 0;
}
找伙伴
题目描述
在班级里,每个人都想找学习伙伴。伙伴不能随便找,都是老师固定好的,老师给出要求:伙伴要凭自己实力去找。
老师给每个人发一张纸,上面有数字。假设你的数字是 \(w\) ,那么如果某位同学手中的数字的所有正约数之和等于 \(w\) ,那么这位同学就是你的小伙伴。
输入格式
输入包含 \(n\) 组数据(最多 \(100\) 组)
对于每组测试数据,输入只有一个数字 \(w\) 。
输出格式
对于每组数据输出两行,第一行包含一个整数 \(m\) ,表示有 \(m\) (如果 \(m=0\) ,只输出一行 \(0\) 即可)个伙伴。
第二行包含相应的 \(m\) 个数,表示伙伴的数字。
注意:小伙伴的数字必须按照升序排列。
样例
样例输入
1
42
样例输出
1
1
3
20 26 41
数据范围与提示
\(100\%\) 的数据,有 \(w\leq 2\times 10^9\) 。
思路
简单的题目,简单的输入输出,嗯,数论,嗯,再见!!!
其实这个题就是用了模拟赛10中 \(T3\) 提到的约数和定理,当时只是求了个个数,这次就是求约数和了,还得记录一下路径。
- 约数和定理的证明:
对于一个大于 \(1\) 的正整数 \(n\) 可以分解质因数:( \(p_i\) 为质数)
\(n=\prod_{i=1}^k p_i^{a_i}={p_1}^{a_1}\times {p_2}^{a_2}\times {p_3}^{a_3}\times ......\times {p_k}^{a_k}\)
\({p_k}^{a_k}\)的约数个数为 \((a_k+1)\) 。
\(n\) 的约数是从 \({p_1}^{a_1},{p_2}^{a_2},{p_3}^{a_3}......{p_k}^{a_k}\) 中每个选一个相乘得到的。
所以 \(n\) 的约数个数为 \(\prod_{i=1}^k (a_i+1)\) 。
所以约数和就是每个中选一个相乘求 \(\sum\) 。
这样我们就可以化简为:
\(f[n]=\prod_{i=1}^k (p_i^0+p_i^1+p_i^2+p_i^3+......+p_i^{a_i})\)
就是约数和定理
首先我们将质数都先线性筛筛出来,你也可以打表,除非你想打 \(1e5\) 的表???
然后对 \(w\) 进行拆分,每拆分出一个质数 \(now*=p_i^{a_i}\) ,当 \(w\) 被拆分成 \(1\) 时,此时的 \(now\) 就是一个答案。
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+50,INF=0x3f3f3f3f;
inline int read(){
int x=0,w=1;
char ch;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
int w;
int prime[maxn+5];
int ans[maxn+5];
int vis[maxn+5];
int tot=0,sum;
void Getprime(){//线性筛
for(int i=2;i<=maxn;i++){
if(!vis[i]){
prime[++tot]=i;
}
for(int j=1;i*prime[j]<=maxn;j++){
vis[i*prime[j]]=1;
if(i%prime[j]==0)break;
}
}
}
bool Judge(int x){
for(int i=2;i<=sqrt(x);i++){
if(x%i==0)return 0;
}
return 1;
}
void DFS(int now,int p,int x){
if(now==1){//被拆分成1
ans[++sum]=x;
return;
}
if(Judge(now-1)&&now>prime[p]){//剪枝,如果now-1为质数,now=(now-1)^0+(now-1)^1,直接加上结果
ans[++sum]=x*(now-1);
}
for(int i=p;prime[i]*prime[i]<=now;i++){//枚举质数
int phi=prime[i];
int cnt=prime[i]+1;//利用公式
for(;cnt<=now;phi*=prime[i],cnt+=phi){
if(now%cnt==0){
DFS(now/cnt,i+1,x*phi);
}
}
}
}
int main(){
Getprime();
while(scanf("%d",&w)==1){
sum=0;
DFS(w,1,1);
sort(ans+1,ans+1+sum);
printf("%d\n",sum);
for(int i=1;i<=sum;i++){
printf("%d ",ans[i]);
}
printf("\n");
}
return 0;
}
string
题目描述
给定一个由小写字母组成的字符串 \(s\) 。
有 \(m\) 次操作,每次操作给定 \(3\) 个参数 \(l,r,x\) 。如果 \(x=1\) ,将 \(s[l]\sim s[r]\) 升序排序;如果 \(x=0\) ,将 \(s[l]\sim s[r]\) 降序排序。你需要求出最终序列。
输入格式
第一行两个整数 \(n,m\) ,表示字符串长度为 \(n\) ,有 \(m\) 次操作。
第二行一个字符串 \(s\) 。
接下来 \(m\) 行每行三个整数 \(l,r,x\) 。
输出格式
一行一个字符串表示答案。
样例
样例输入
5 2
cabcd
1 3 1
3 5 0
样例输出
abdcc
数据范围与提示
对于 \(40\%\) 的数据, \(n,m\leq 1000\) 。
对于 \(100\%\) 的数据, \(n,m\leq 100000\) 。
思路
- \(40opts\)的分段
直接用 \(sort\) 就可以了,简单通俗,分价比较高。
- \(100opts\)的分段
很明显的线段树,但是有那么一点考验思维,我们在建树的时候,若左右两个端点的字符相同,则父节点就存这个字符的值,若不同,父节点存为 \(0\) ,当我们访问的时候,若有值,直接输出 \(r-l+1\) 个本字符。
如下图:
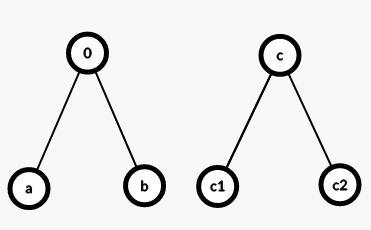
代码
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+50,INF=0x3f3f3f3f;
inline int read(){
int x=0,w=1;
char ch;
for(;ch<'0'||ch>'9';ch=getchar()) if(ch=='-') w=-1;
for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';
return x*w;
}
int n,m;
char a[maxn];
struct Tree{
int l,r,w;
}e[maxn<<2];
int cnt[30];
void Build(int rt,int l,int r){//建树
e[rt].l=l,e[rt].r=r;
if(l==r){
e[rt].w=a[l]-'a'+1;//存值
return;
}
int mid=(l+r)>>1;
Build(rt<<1,l,mid);//左子树存值
Build(rt<<1|1,mid+1,r);//右子树存值
if(e[rt<<1].w==e[rt<<1|1].w){//若左右子树的值相同,父节点存该值
e[rt].w=e[rt<<1].w;
}
}
void Init(int rt,int l,int r){//记录每个字母的数量
if(e[rt].l>=l&&e[rt].r<=r&&e[rt].w!=0){
cnt[e[rt].w]+=e[rt].r-e[rt].l+1;
return;
}
if(e[rt].w!=0){
e[rt<<1].w=e[rt<<1|1].w=e[rt].w;
}
int mid=(e[rt].l+e[rt].r)>>1;
if(l<=mid){
Init(rt<<1,l,r);
}
if(r>mid){
Init(rt<<1|1,l,r);
}
}
void Change(int rt,int l,int r,int w){//修改区间
if(e[rt].l>=l&&e[rt].r<=r||e[rt].w==w){
e[rt].w=w;
return;
}
if(e[rt].w!=0){
e[rt<<1].w=e[rt<<1|1].w=e[rt].w;
e[rt].w=0;
}
int mid=(e[rt].l+e[rt].r)>>1;
if(l<=mid){
Change(rt<<1,l,r,w);
}
if(r>mid){
Change(rt<<1|1,l,r,w);
}
if(e[rt<<1].w==e[rt<<1|1].w){
e[rt].w=e[rt<<1].w;
}
}
void COUT(int rt){//输出
if(e[rt].w!=0){
for(int i=e[rt].l;i<=e[rt].r;i++){
printf("%c",e[rt].w+'a'-1);
}
return;
}
COUT(rt<<1);
COUT(rt<<1|1);
}
int main(){
n=read(),m=read();
scanf("%s",a+1);
Build(1,1,n);
while(m--){
int l=read(),r=read(),opt=read();
memset(cnt,0,sizeof(cnt));
Init(1,l,r);
if(opt==1){
for(int i=1;i<=26;i++){//正序排序
if(cnt[i]!=0){
Change(1,l,l+cnt[i]-1,i);
l+=cnt[i];
}
}
}else{
for(int i=26;i>=1;i--){//降序排序
if(cnt[i]!=0){
Change(1,l,l+cnt[i]-1,i);
l+=cnt[i];
}
}
}
}
COUT(1);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号