P3842 [TJOI2007]线段——线性dp

P3842 [TJOI2007]线段

题目描述

在一个 \(n\times n\) 的平面上，在每一行中有一条线段，第 \(i\) 行的线段的左端点是 \((i, L(i))\)，右端点是 \((i, R(i))\)，其中 \(1\leq L(i)\leq R(i)\leq n\)。

你从 \((1, 1)\) 点出发，要求沿途走过所有的线段，最终到达 \((n, n)\) 点，且所走的路程长度要尽量短。

更具体一些说，你在任何时候只能选择向下走一步（行数增加 \(1\)）、向左走一步（列数减少 \(1\)）或是向右走一步（列数增加 \(1\)）。当然，由于你不能向上行走，因此在从任何一行向下走到另一行的时候，你必须保证已经走完本行的那条线段。

输入格式

输入文件的第一行有一个整数 \(n\)，以下 \(n\) 行，在第 \(i\) 行（总第 \(i+1\) 行）的两个整数表示 \(L(i)\) 和 \(R(i)\)。

输出格式

输出文件仅包含一个整数，你选择的最短路程的长度。

输入输出样例

输入

6
2 6
3 4
1 3
1 2
3 6
4 5

输出

24

说明/提示

我们选择的路线是

\((1,1)->(1,6)\)
\((2,6)->(2,3)\)
\((3,3)->(3,1)\)
\((4,1)->(4,2)\)
\((5,2)->(5,6)\)
\((6,6)->(6,4)->(6,6)\)

不难计算得到，路程的总长度是 \(24\)。

\(100\%\) 的数据中，\(n\leq 20,000\)。

思路

不难看出，路程长度由两个部分组成：左右走的距离 \(+\) 上下走的距离，因为上下走的距离一定是 \(n\)，所以我们只需要求出左右走的最小距离即可。

很明显，当我们走完一行的线段时，我们会处在左端点/右端点，这样我们就需要在线性 \(dp\) 的基础上加一维来表示走完这一行处在左/右端点。

所以我们定义一个 \(f[i][0/1]\)，表示走完第 \(i\) 行的线段后，我们处在左/右端点。

然后我们就可以用上一行的状态来推出下一行了。

分为 \(4\) 种情况：

上一行在左端点，下一行走到左端点；
上一行在左端点，下一行走到右端点；
上一行在右端点，下一行走到左端点；
上一行在右端点，下一行走到右端点；

我们以"上一行在右端点，下一行走到右端点"为例：

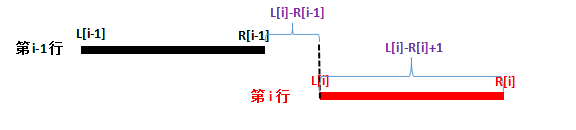
这样我们就可以推出状态转移方程了。

f[i][1]=min(f[i-1][1]+abs(l[i]-r[i-1])+r[i]-l[i]+1,f[i-1][0]+abs(l[i]-l[i-1])+r[i]-l[i]+1);//本行走到右端点，上一行走到左/右端点，取最小值
f[i][0]=min(f[i-1][1]+abs(r[i]-r[i-1])+r[i]-l[i]+1,f[i-1][0]+abs(r[i]-l[i-1])+r[i]-l[i]+1);//本行走到左端点，上一行走到左/右端点，取最小值

最后不要忘了初始化第 \(1\) 行就可以了。

代码

#include <bits/stdc++.h>
using namespace std;

const int maxn=2e4+50;
int n;
int l[maxn],r[maxn];
int f[maxn][2];

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d%d",&l[i],&r[i]);
    }
    f[1][0]=2*r[1]-l[1]-1;//第1行往返，走到右端点再回来
    f[1][1]=r[1]-1;//直接走到右端点
    for(int i=2;i<=n;i++){
        f[i][1]=min(f[i-1][1]+abs(l[i]-r[i-1])+r[i]-l[i]+1,f[i-1][0]+abs(l[i]-l[i-1])+r[i]-l[i]+1);//本行走到右端点，上一行走到左/右端点，取最小值
        f[i][0]=min(f[i-1][1]+abs(r[i]-r[i-1])+r[i]-l[i]+1,f[i-1][0]+abs(r[i]-l[i-1])+r[i]-l[i]+1);//本行走到左端点，上一行走到左/右端点，取最小值
    }
    printf("%d\n",min(f[n][1]+n-r[n],f[n][0]+n-l[n]));//因为最后还要走到(n,n)的地方，加上剩下的距离，再加上上下走的距离即可
    return 0;
}