DeepLearning---Hyper Parameters Optimization

超参数优化

超参数在很大程度上可以决定模型的训练效果，例如学习率影响学习效率，正则化影响泛化能力等。
对超参数的优化也一直是一个受人关注的问题，尤其是可调整的超参数越来越多，手动调参的消耗越来越大，迫切需要一些可以自动化搜索最佳超参数的算法。
本文将介绍几种常用的超参数优化算法。

Grid Search

网格搜索是最简单也是最容易理解的超参数优化算法。
当我们面对调参的时候，我们自然而然的就会想到把各种超参数的候选值全部尝试一遍，对比他们的实际效果，然后从中挑选出最佳的超参数组合，网格搜索就是这样的一种思想。
对于每个超参数，其都会有多个候选值，这些候选值可能是根据经验人为选定的，也可能是在一个合理范围内均匀选取的。通过对这些超参数排列组合，构建一个高维的超参数表格，然后遍历其中所有的组合，找出最佳的超参数配置。

例如，对于 learning_rate 和 batch_size 两个超参数，其候选值就可以两两组合构建一个二维表格，遍历表格就可以搜索出最佳超参数组合。

然而这种方法的计算消耗非常大，每增加一个超参数，计算时间都是指数级上升。

Random Search

随机搜索和网格搜索类似，采用同样的方式构建一个超参数表格，或者说搜索空间，对于每个超参数，每次随机选一个候选值，或者说每次在搜索空间中随机选取一个超参数组合，做一次评估，最后选出最好的组合。
该算法的尝试次数 \(N\) 人为指定，当 \(N\) 足够大的时候其行为类似于网格搜索，过小时则没有好的效果，比较依赖经验。

综合考虑各种因素，随机搜索的算法通常优于网格搜索，即在不大的消耗下可以得到较好的超参数组合。
当没有好的搜索算法时应当有限尝试该算法。

Bayesian Optimization

贝叶斯优化，其核心思想是构建一个从超参数到目标函数（或其他的评估指标）的映射。可以理解为，有这样一个函数，每一个自变量是我的一个超参数组合，对应的因变量是我的损失或者其他的评估指标。贝叶斯优化就是学习出这个函数，然后找到其中的极值。

看下面一个图

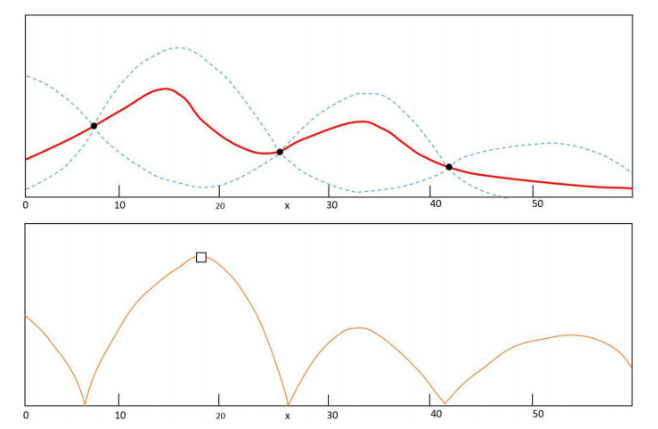
图中横坐标为超参数取值，纵坐标为模型评估指标，三个黑色点是已经计算过的点。算法会根据已经计算过的点来预测其他未知点的可能取值，红线表示预估的均值，蓝色虚线表示预估的波动范围，上下各一个标准差，不难看出，越靠近已经计算过的点，预估的误差越小，越远离预估的波动范围越大。之后根据均值和标准差，可以构建一个采集函数，即第二个子图所示，采集函数描述了第一个子图中某一点取到极值的概率，根据采集函数取下一个要计算的点。

上述过程就是贝叶斯优化的核心，其具体实现原理此处不再赘述，因为该方法的性价比在很多情况下不如随机搜索。