2020 Multi-University Training Contest 4 1007 Go Running(网络流)
题目
http://acm.hdu.edu.cn/showproblem.php?pid=6808
题意
在一个二维空间中,有一种检测机器,可以告诉你在 t 时刻 x 位置有人跑步经过。已知人跑步速度为 1 m/s,现给出 n 个机器的检测数据,问最少有多少人在跑步。
题解
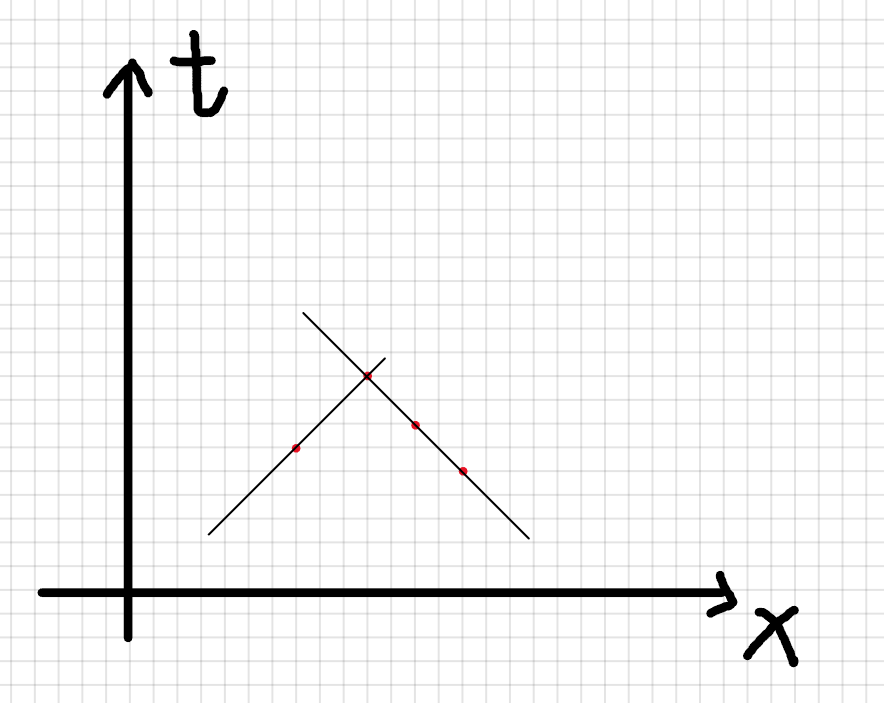
由每个机器数据可知若要在 t 时刻 x 位置能检测到,那么只有在 0 时刻 x - t 位置向正方向移动 和 x + t 位置向负方向移动两种情况,当我们将 x 和 t 作为坐标画到坐标轴上时,如下图所示。由于速度为 1 m/s,所以能够很快发现被斜率为 1 或 -1 的直线同时穿过的点能够只用一个人就够了。所以本题就变成了用最少数量的斜率为 1 或 -1 的直线覆盖所有的点,那么我们这时候将 x - t(斜率为1)和 x + t(斜率为-1) 作为二分图两边的匹配点,由 x - t 的点向 x + t 的点引出一条边,题目就变为了求二分图的最小点覆盖为题,而最小点覆盖就等于最大匹配数,也就是最大网络流问题。
#include <bits/stdc++.h>
// #include <iostream>
// #include <cstring>
// #include <string>
// #include <algorithm>
// #include <cmath>
// #include <cstdio>
// #include <queue>
// #include <stack>
// #include <map>
// #include <bitset>
// #include <set>
// #include <vector>
// #include <iomanip>
#define ll long long
#define ull unsigned long long
#define met(a, b) memset(a, b, sizeof(a))
#define rep(i, a, b) for(int i = a; i <= b; ++i)
#define bep(i, a, b) for(int i = a; i >= b; --i)
#define lowbit(x) (x&(-x))
#define MID (l + r) / 2
#define ls pos*2
#define rs pos*2+1
#define pb push_back
#define ios() ios::sync_with_stdio(0), cin.tie(0), cout.tie(0)
using namespace std;
const int maxn = 1e6 + 1010;
const int inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3f;
const ll mod = 1e9 + 7;
const double eps = 1e-6;
const double PI = acos(-1);
struct node {
ll x, t;
}arr[maxn];
struct Edge {
int to;
int flow;
int net;
}edge[maxn*2];
int head[maxn*2], cnt;
int cpy[maxn];
int lv[maxn];
ll b[maxn], tail;
queue<int> que;
void addedge(int u, int v, int flow) {
edge[cnt] = (Edge){v, flow, head[u]};
head[u] = cnt++;
edge[cnt] = (Edge){u, 0, head[v]};
head[v] = cnt++;
}
int bfs(int s, int e) {
rep(i, 0, 2*tail + 1) lv[i] = 0;
while(!que.empty()) que.pop();
que.push(s);
lv[s] = 1;
while(!que.empty()) {
int t = que.front();
que.pop();
for(int i = head[t]; i != -1; i = edge[i].net) {
int to = edge[i].to;
if(!lv[to] && edge[i].flow) {
lv[to] = lv[t] + 1;
que.push(to);
}
}
if(lv[e]) return 1;
}
return 0;
}
int dfs(int s, int e, int limit) {
if(s == e || !limit) return limit;
int flow = 0;
int minn;
for(int &i = head[s]; i != -1; i = edge[i].net) {
int to = edge[i].to;
if(lv[to] == lv[s] + 1 && (minn = dfs(to, e, min(limit, edge[i].flow)))) {
flow += minn;
edge[i].flow -= minn;
edge[i^1].flow += minn;
limit -= minn;
if(!limit) break;
}
}
return flow;
}
int dinic(int s, int e) {
int maxflow = 0;
memcpy(cpy, head, sizeof(int) * (2*tail + 1));
while(bfs(s, e)) {
maxflow += dfs(s, e, inf);
memcpy(head, cpy, sizeof(int) * (2*tail + 1));
}
return maxflow;
}
int main() {
int T;
scanf("%d", &T);
while(T--) {
tail = 0;
int n;
scanf("%d", &n);
rep(i, 1, n) {
cin >> arr[i].x >> arr[i].t;
b[++tail] = arr[i].x - arr[i].t;
b[++tail] = arr[i].x + arr[i].t;
}
sort(b + 1, b + 1 + tail);
tail = unique(b + 1, b + 1 + tail) - b - 1;
cnt = 0;
rep(i, 0, 2*tail + 1) head[i] = -1;
rep(i, 1, tail) {
addedge(0, i, 1);
addedge(i + tail, 2*tail + 1, 1);
}
rep(i, 1, n) {
int u = lower_bound(b + 1, b + 1 + tail, arr[i].x - arr[i].t) - b;
int v = lower_bound(b + 1, b + 1 + tail, arr[i].x + arr[i].t) - b + tail;
// cout << u << ' ' << v << "---" << endl;
addedge(u, v, 1);
}
cout << dinic(0, 2*tail + 1) << endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号