18.10.30 考试总结
这段时间我都好没有状态啊...。汪汪大哭 思路都是对的 然而总写挂写挂写挂 我真的难受。

通过打表发现 每一个满足条件的数对$(a, b), a > b$同时满足这样一个条件
$gcd(a, b) = a xor b = c = (a - b)$
所以考虑枚举$c$ 从$j = 2 ~ [n / c]$ 每次判断$j * c xor (j - 1) * c$是否等于$c$即可
由调和计数可以证明时间复杂度约为$O(nlnn)$
代码
#include <bits/stdc++.h> using namespace std; int n, ans; int main( ) { freopen("gcd.in", "r", stdin); freopen("gcd.out", "w", stdout); scanf("%d",& n); for(int c = 1;c <= n;c ++) { for(int j = 2;j <= (n / c);j ++) { int p1 = c * j, p2 = c * (j - 1); if((p1 ^ p2) == c) ans ++; } } printf("%d\n", ans); }

就是这道题 我明明是想出来怎么做的然而由于重心求错了就全部gg 我无fuck说:)
首先肯定是套点分治的板子 每次对于当前重心处理的时候对于它的每个子树处理两次 第一次跑的时候统计它与别的路径所能构成的答案
具体来说就是先跑出当前$dis$ 在一个有序的容器中找出和刚好大于$S$的路径 也就是说在这个容器中$lower_bound(S - dis)$
这个容器可以使用$set$ 第二次跑的时候 我们就将目前跑出来的路径压到$set$里面即可
不能同时统计答案同时压 否则会统计到自己
代码
#include <bits/stdc++.h> #define il inline #define rg register #define oo 1e9 using namespace std; const int N = 1e5 + 5; int head[N], nex[2 * N], tov[2 * N], val[2 * N]; int tot, n, S, E, size[N], siz[N], Num, ma, st; int dis[N], cnt, ans; bool vis[N]; set<int>h; il int read( ) { int t = 1, ans = 0; char x; x = getchar( ); while(x < '0' || x > '9') { if(x == '-') t = -1; x = getchar( ); } while(x >= '0' && x <= '9') { ans = ans * 10 + x - '0'; x = getchar( ); } return ans * t; } il void add(int u, int v, int w) { tot ++; nex[tot] = head[u]; tov[tot] = v; head[u] = tot; val[tot] = w; } il void Init( ) { n = read( ), S = read( ), E = read( ); for(rg int i = 1;i < n;i ++) { int u, v, w; u = read( ), v = read( ), w = read( ); add(u, v, w); add(v, u, w); } } il void find_st(int u, int fa) { size[u] = 1; int tmp = 0; for(rg int i = head[u];i;i = nex[i]) { int v = tov[i]; if(vis[v] || v == fa) continue; find_st(v, u); size[u] += size[v]; tmp = max(tmp, size[v]); } tmp = max(Num - size[u], tmp); if(tmp < ma) st = u, ma = tmp; } il void get_dis(int u, int fa, int tag) { if(tag) h.insert(dis[u]); else { if(dis[u] < S) { set<int> :: iterator it; it = h.lower_bound(S - dis[u]); int c = *it, d = h.size( ); if(d && c + dis[u] <= E && c + dis[u] >= S) ans = min(ans, c + dis[u]); } else if(dis[u] <= E) ans = min(ans, dis[u]); } for(rg int i = head[u];i;i = nex[i]) { int v = tov[i]; if(v == fa || vis[v]) continue; dis[v] = dis[u] + val[i]; if(dis[v] > S) {if(dis[v] <= E) ans = min(ans, dis[v]); continue ;} get_dis(v, u, tag); } } il void dfs(int u) { vis[u] = true; memset(dis, 0, sizeof(dis)); h.clear( ); for(rg int i = head[u];i;i = nex[i]) { int v = tov[i]; if(vis[v]) continue; dis[v] = val[i]; get_dis(v, u, 0); get_dis(v, u, 1); } for(rg int i = head[u];i;i = nex[i]) { int v = tov[i]; if(vis[v]) continue; Num = siz[v]; ma = oo; find_st(v, u); dfs(st); } } il void dfs1(int u, int fa) { siz[u] = 1; for(rg int i = head[u];i;i = nex[i]) { int v = tov[i]; if(v == fa) continue; dfs1(v, u); siz[u] += size[v]; } } il void Solve( ) { ans = oo; Num = n; ma = oo; find_st(1, 0); dfs1(1, 0); dfs(st); if(ans <= E) printf("%d\n", ans); else printf("-1\n"); } int main( ) { freopen("path.in", "r", stdin); freopen("path.out", "w", stdout); Init( ); Solve( ); }

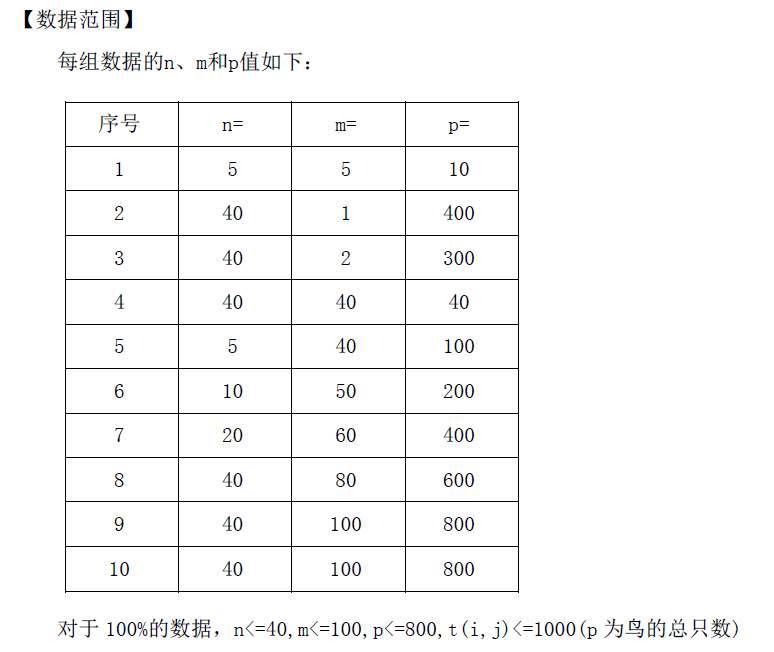
这道题一看就是四川的一道省选题修车好不好!!!!! 考场上一看就知道了但是仍然没有写出来 考完发现这是[NOI2012]美食节...。
这道题和修车的差别就是这道题相距修车他的数据范围变大了不少 所以怎么解决这个问题呢
选择网络流动态加点 原始建图是每个师傅拆成$n$个点 每个点表示这个师傅目前在修倒数第$x$辆车 也就是排在它后面的人都需要等待 他们这一轮等待时间为$x * val$
$val$是当前车被这个师傅修的时间 所以每个人都需要和这个师傅连边 边权为$x * val$ 流量为$1$ 然后每个人向原点连边 每个拆完的师傅向终点连边 边权$0$ 流量$1$
这道题呢 这道题因为数据太大 所以一开始我们只建出每个师傅修倒数第一辆车的点 跑完每次假设师傅$x$被使用了 那么下次这个师傅就只能倒数第次数加一修下一辆车了
那么我们就要新建出该师傅对应的下一个次数的节点 继续跑就可以了 至于为什么是从倒数第一个开始 倒数第一个产生的费用肯定是最小的 所以从小到大搞
代码
#include <bits/stdc++.h> #define oo 1e9 using namespace std; const int N = 90000 + 5; const int M = 5000000 + 5; int tot = 1, nex[M], tov[M], f[M], val[M]; int head[N], n, m, p[N], tag[N], a[50][200], src, sink; int dis[N], ev[N], ee[N], V, ans, x[N], cnt; bool vis[N]; queue<int>Q; int read( ) { int t = 1, ans = 0; char x; x = getchar( ); while(x < '0' || x > '9') { if(x == '-') t = -1; x = getchar( ); } while(x >= '0' && x <= '9') { ans = ans * 10 + x - '0'; x = getchar( ); } return ans * t; } void add(int u, int v, int fl, int w) { tot ++; nex[tot] = head[u]; f[tot] = fl; tov[tot] = v; val[tot] = w; head[u] = tot; tot ++; nex[tot] = head[v]; tov[tot] = u; f[tot] = 0; val[tot] = -w; head[v] = tot; } void Init( ) { n = read( ), m = read( ); for(int i = 1;i <= n;i ++) p[i] = read( ); for(int i = 1;i <= m;i ++) x[i] = 1; for(int i = 1;i <= n;i ++) for(int j = 1;j <= m;j ++) a[i][j] = read( ); src = n + m + 1, sink = n + m + 2; cnt = n + m + 2; for(int i = 1;i <= n;i ++) { add(src, i, p[i], 0); tag[i] = 1; for(int j = 1;j <= m;j ++) { add(i, j + n, 1, a[i][j]); tag[j + n] = j + n; } } for(int i = 1;i <= m;i ++) add(n + i, sink, 1, 0); } bool spfa( ) { for(int i = 1;i <= cnt;i ++) dis[i] = 2 * oo; for(int i = 1;i <= cnt;i ++) vis[i] = false; int cmp = dis[sink]; vis[src] = true; Q.push(src); dis[src] = 0; while(! Q.empty( )) { int u = Q.front( ); Q.pop( ); vis[u] = false; for(int i = head[u];i;i = nex[i]) { int v = tov[i]; if(dis[v] > dis[u] + val[i] && f[i]) { dis[v] = dis[u] + val[i]; ev[v] = u, ee[v] = i; if(! vis[v]) { Q.push(v); vis[v] = true; } } } } return dis[sink] < cmp; } void argu( ) { int u = sink, delta = oo; V = tag[ev[sink]] - n; while(u != src) { delta = min(delta, f[ee[u]]); u = ev[u]; } u = sink; while(u != src) { f[ee[u]] -= delta; f[ee[u] ^ 1] += delta; u = ev[u]; } ans += delta * dis[sink]; } void re_add( ) { x[V] ++; cnt ++; for(int i = 1;i <= n;i ++) add(i, cnt, 1, x[V] * a[i][V]); add(cnt, sink, 1, 0); tag[cnt] = V + n; } void Solve( ) { while(spfa( )) { argu( ); re_add( ); } printf("%d\n", ans); } int main( ) { freopen("bird.in", "r", stdin); freopen("bird.out", "w", stdout); Init( ); Solve( ); }


