18.10.29 考试总结
今天考试我没有一道题想出正解了...。 听了idy的话今天先把暴力搞了狗了标准100暴力分竟然没有垫底..

这道题其实要多暴力有多暴力...。 正解是开26棵线段树 每一个字母对应一棵线段树
每次搞一个区间首先把他所有的字母取出来 然后填回去 当然不是暴力填 仍然是区间填 每个的填法都是从小到大填
所以每次填完要打上标记 若下次递归到这里下放标记即可
代码
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 5; char s[N]; int tag[4 * N], n, m; struct node { int sum[26]; node operator + (const node & b) const { node a; for(int i = 0;i < 26;i ++) a.sum[i] = b.sum[i] + sum[i]; return a; } }zero, K, f[4 * N]; int read( ) { int t = 1, ans = 0; char x; x = getchar( ); while(x < '0' || x > '9') { if(x == '-') t = -1; x = getchar( ); } while(x >= '0' && x <= '9') { ans = ans * 10 + x - '0'; x = getchar( ); } return ans * t; } void update(int o) { f[o] = f[2 * o] + f[2 * o + 1]; } void build(int o, int l, int r) { if(l == r) { f[o].sum[s[l] - 'a'] ++; return ; } int mid = l + r >> 1; build(o << 1, l, mid); build(o << 1 | 1, mid + 1, r); update(o); } node giv(node & x, int size) { node tmp = zero; for(int i = 0;i < 26;i ++) { if(size < x.sum[i]) {x.sum[i] -= size; tmp.sum[i] += size; return tmp;} tmp.sum[i] += x.sum[i]; size -= x.sum[i]; x.sum[i] = 0; } } void push_down(int o, int l, int r) { int mid = l + r >> 1; if(tag[o]) { tag[o << 1] = tag[o << 1 | 1] = tag[o]; node tmp = f[o]; if(tag[o] == -1) { f[o << 1 | 1] = giv(tmp, r - mid); f[o << 1] = tmp; } else { f[o << 1] = giv(tmp , mid - l + 1); f[o << 1 | 1] = tmp; } tag[o] = 0; } } node query(int o, int l, int r, int L, int R) { if(l >= L && r <= R) return f[o]; int mid = l + r >> 1; push_down(o, l, r); node ans = zero; if(L <= mid) ans = ans + query(o << 1, l, mid, L, R); if(mid < R) ans = ans + query(o << 1 | 1, mid + 1, r, L, R); update(o); return ans; } void get_tag(int o, int l, int r, int L, int R, int opt) { if(l >= L && r <= R) { tag[o] = opt; f[o] = giv(K, r - l + 1); return ; } push_down(o, l, r); int mid = l + r >> 1; if(opt == 1) { if(L <= mid) get_tag(o << 1, l, mid, L, R, opt); if(mid < R) get_tag(o << 1 | 1, mid + 1, r, L, R, opt); } else { if(mid < R) get_tag(o << 1 | 1, mid + 1, r, L, R, opt); if(L <= mid) get_tag(o << 1, l, mid, L, R, opt); } update(o); } void dfs(int o, int l, int r) { if(l == r) { for(int i = 0;i < 26;i ++) if(f[o].sum[i]) {printf("%c",i + 'a');} return ; } push_down(o, l, r); int mid = l + r >> 1; dfs(o << 1, l, mid); dfs(o << 1 | 1, mid + 1, r); } int main( ) { freopen("string.in", "r", stdin); freopen("string.out", "w", stdout); scanf("%d%d",& n,& m); scanf("%s",s + 1); build(1, 1, n); while(m --) { int l, r, opt; l = read( ), r = read( ), opt = read( ); if(! opt) opt = -1; K = query(1, 1, n, l, r); get_tag(1, 1, n, l, r, opt); } dfs(1, 1, n); }

这道题是一道很日怪的$dp$
$dp[i][j]$表示到了第$i$列有$j$列没有填的合法方案数
那么$i$越过一个左侧区间的右端点时,从之前剩下空列中选一在这个左侧区间放1。转移时分在右侧区间放1或不放1。
代码
#include <bits/stdc++.h> using namespace std; const int N = 3003; const long long MOD = 998244353; int F[N], G[N], n, m, lef, tot; long long dp[N][N]; int main( ) { freopen("matrix.in", "r", stdin); freopen("matrix.out", "w", stdout); scanf("%d%d",& n,& m); for(int i = 1;i <= n;i ++) { int l, r; scanf("%d%d",& l,& r); F[l] ++; G[r] ++; } dp[0][0] = 1; for(int i = 1;i <= m;i ++) { lef ++; tot += G[i]; for(int j = G[i];j <= tot;j ++) dp[i][j] = dp[i - 1][j - G[i]]; for(int j = 1;j <= tot;j ++) dp[i][j - 1] = (dp[i][j - 1] + dp[i][j] * j % MOD) % MOD; for(int j = 1;j <= F[i];j ++) { for(int k = 0;k <= tot;k ++) dp[i][k] = dp[i][k] * max(lef - (tot - k), 0) % MOD; lef --; } } printf("%lld\n", dp[m][0]); }

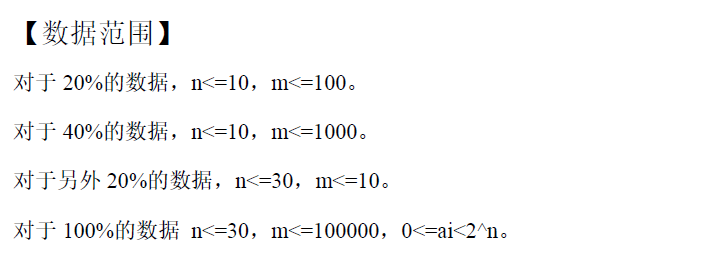
这道题首先对对手操作进行化简 原式子的$x$可以分为两种情况
1.$x$的第$n$位为$1$ 也就是说它乘以二之后模上$2^{n}$为$1$ 后面的$2 * x$相当于$x$左移一位 所以这个操作相当于把$x$最高位取出来挤到最后一位
2.$x$的第$n$位为$0$ 那么这个时候他乘以二模上$2 ^ {n}$不变 他除以$2 ^ {n}$则为0 同样相当于把他的最高位取出来挤到最后
先不考虑异或上给定的数
因为异或是相互独立的 所以在进行这个操作的时候相当于先把前面位置的$a[i]$分别进行上述操作再异或起来 所以这个时候会产生$m + 1$个值与给定数进行异或 因为有$m + 1$个断点
那么这个时候就可以对这$m + 1$个数建一棵深度为$n$的$trie$ 然后在这个上面$dfs$
若到达某一个深度时他有两个儿子 那么他对答案不会做出贡献 因为不论我这一位选择什么我的对手都可以选择另外一边将我吃掉
那么若这一位只有一个儿子 就可以产生$(1 << (dep - 1))$的贡献 因为对手只有一种选择 我选择与他相反的即可
一直走到叶子节点 统计对于每个叶子节点的答案的最大值 因为最小值是在$dfs$过程中已经保证了
代码
#include <bits/stdc++.H> using namespace std; const int N = 3e6 + 5; int ans, num, cnt, son[N][2], n, m, rsum[N], sum[N], a; bool vis[N]; void insert(int x) { int now = 0; for(int i = n;i >= 1;i --) { int nd = x & (1 << (i - 1)) ? 1 : 0; if(! son[now][nd]) son[now][nd] = ++ cnt; now = son[now][nd]; } vis[now] = true; } void dfs(int nd, int tmp, int dep) { if(vis[nd]) { if(tmp > ans) ans = tmp, num = 1; else if(tmp == ans) num ++; return ; } if(son[nd][1] && son[nd][0]) { dfs(son[nd][1], tmp, dep - 1); dfs(son[nd][0], tmp, dep - 1); } else if(son[nd][1]) dfs(son[nd][1], tmp + (1 << (dep - 1)), dep - 1); else dfs(son[nd][0], tmp + (1 << (dep - 1)), dep - 1); } int main( ) { freopen("big.in", "r", stdin); freopen("big.out", "w", stdout); scanf("%d%d",& n,& m); for(int i = 1;i <= m;i ++) { scanf("%d",& a); int h = (a & (1 << (n - 1))) ? 1 : 0; int r = ((a ^ (h << (n - 1))) << 1) | h; sum[i] = sum[i - 1] ^ a; rsum[i] = rsum[i - 1] ^ r; } for(int i = 0;i <= m;i ++) { int p = rsum[i] ^ sum[m] ^ sum[i]; insert(p); } dfs(0, 0, n); printf("%d\n%d\n", ans, num); }


