18.10.15 考试总结

今天考试是真的难 我fo了 每道题都有思路 但是 每 道 题 都 没 有 搞 粗 来！！！ 我恨

这道题是一道dp 我已经接近正解了讲真 但是考场上全在想T2T3了 生气

首先有一些很明显的性质

1.第$i$列与第$i + k * n$列的棋子数量一定是一样的 否则无法保证任意一个$n * n$的矩阵内棋子数相等

 2.棋子可以随便乱搞 相当于求一个组合数

所以$dp[i][j]$表示到第$i$列总共放了$j$个棋子的方案数 不用一列一列的求 因为已知某些列是一样的 所以可以直接求出组合数的幂

即 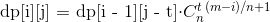 预处理出即可 

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const ll MOD = 1e9 + 7;
ll m, C[105][105], Coe[105][105], dp[105][10005];
int n, c;

ll fast_pow(ll a, ll b) {
    
    ll ans = 1;
    for(;b;b >>= 1, a = a * a % MOD)
        if(b & 1) ans = ans * a % MOD;
    return ans;
}

void Init( ) {
    
    scanf("%d%lld%d",& n,& m,& c);
    C[0][0] = 1;
    for(int i = 1;i <= 100;i ++) {
        C[i][0] = C[i][i] = 1;
        for(int j = 1;j < i;j ++) {
            C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
            if(C[i][j] >= MOD) C[i][j] -= MOD;
        }
    }
    for(int i = 1;i <= n;i ++) {
        ll p = (m - i) / n + 1;
        for(int j = 0;j <= n;j ++) {
            Coe[i][j] = fast_pow(C[n][j], p);
        }
    }
}

void Solve( ) {
    
    dp[0][0] = 1;
    for(int i = 1;i <= n;i ++) {
        for(int j = 0;j <= i * n && j <= c;j ++) {
            int L = min(j, n);
            for(int k = 0;k <= L;k ++) {
                dp[i][j] += dp[i - 1][j - k] * Coe[i][k] % MOD;
                if(dp[i][j] >= MOD) dp[i][j] -= MOD;
            }
        }
    }
    printf("%lld\n", dp[n][c]);
}

int main( ) {
    
    freopen("chess.in","r",stdin);
    freopen("chess.out","w",stdout);
    Init( );
    Solve( );
}

这道题一开始总觉得自己是可以想出来的 结果想了半天在fyt大佬的帮助下只想出个垃圾被卡空间的$nlog$算法

暂且不提 

这道题真的是一个很聪明的算法 我们倒着来稿 对于每一个值都将他入栈 维护一个单调递增的序列 相当于维护每一个合法最长区间的右端点

因为每次维护栈的时候要$pop$所以在进行这个操作的时候进行答案的更新 因为这个元素被弹出 也就是说他比当前的元素要小 他的区间的左端点肯定在当前元素到栈顶之间

所以对于每一个栈顶 我们维护他到栈中下一个元素区间的最小元素 因为只有最小元素才能更新答案 若他后面有比他更小的就会不合法

每次弹的时候将它到栈顶元素的这段区间与栈顶元素到下一个元素的这段区间的最小值和位置合并即可

第一个元素要赋极大值 保证所有元素都被弹出 即都会被更新

代码

#include <bits/stdc++.h>
#define oo 1e9
using namespace std;

const int N = 1e7 + 5;
int val[N], stk[N], pos[N], n, a[N], ans = 1, top;

int read( ) {
    
    int t = 1, ans = 0;
    char x; x = getchar( );
    while(x < '0' || x > '9') {
        if(x == '-') t = -1;
        x = getchar( );
    }
    while(x >= '0' && x <= '9') {
        ans = ans * 10 + x - '0';
        x = getchar( );
    }
    return ans * t;
}

void Solve( ) {
    
    stk[++ top] = n, pos[top] = n, val[top] = a[n];
    for(int i = n - 1;i >= 1;i --) {
        int mival = a[i + 1], mipos = i + 1;
        while(top && a[stk[top]] < a[i]) {
            ans = max(ans, stk[top] - mipos + 1);
            if(val[top] < mival) {
                mival = val[top]; mipos = pos[top];
            }
            top --;
        }
        if(! top) {
            stk[++ top] = i, pos[top] = i, val[top] = a[i]; continue;
        }
        if(a[i] <= mival) {
            mival = a[i]; mipos = i;
        }
        stk[++ top] = i, pos[top] = mipos, val[top] = mival;
    }
    printf("%d\n", ans);
}

int main( ) {
    
    freopen("array.in","r",stdin);
    freopen("array.out","w",stdout);
    scanf("%d",& n); n ++; a[1] = oo;
    for(int i = 2;i <= n;i ++) a[i] = read( );
    Solve( );
}

这道题其实是一道回滚莫队板子我觉得 就是因为两端值域合并之后删除不方便 所以使用回滚莫队

就是每次固定一个边界 边界内左边的块内元素每次重新加进去 块外的信息保留

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;
int blo[N], a[N], vis[N], idc, ll[N], rr[N];
int stk[N], top, ans[N], n, m, b, now_ans;
bool arr[N];
struct ques {
    
    int l, r, id;
}q[N], Q[N];

bool cmp(const ques & a, const ques & b) {
    
    return blo[a.l] == blo[b.l] ? a.r < b.r : a.l < b.l;
}

void Init( ) {
    
    scanf("%d%d",& n,& m);
    b = sqrt(n);
    for(int i = 1;i <= n;i ++) {
        scanf("%d",& a[i]); blo[i] = (i + b - 1) / b;
    }
    for(int i = 1;i <= m;i ++) {
        scanf("%d%d",& q[i].l, & q[i].r);
        q[i].id = i;
    }
    sort(q + 1, q + m + 1, cmp);
}

bool cmp_r(const ques & a, const ques & b) {
    
    return a.r == b.r ? a.l < b.l : a.r < b.r;
}

void update(int u) {
    
    if(vis[u] != idc) vis[u] = idc, ll[u] = u, rr[u] = u, arr[u] = false;
}

void work(int link, bool tag) {
    
    update(link), update(link + 1), update(link - 1);
    int tmp_l = link, tmp_r = link;
    if(link != 1 && arr[link - 1]) tmp_l = ll[link - 1];
    if(link != n && arr[link + 1]) tmp_r = rr[link + 1];
    now_ans = max(now_ans, tmp_r - tmp_l + 1);
    ll[tmp_r] = tmp_l, rr[tmp_l] = tmp_r, arr[link] = true;
    if(tag) stk[++ top] = link;
}

void restore( ) {
    
    while(top) {
        int link = stk[top];
        if(link != 1 && arr[link - 1]) rr[ll[link - 1]] = link - 1;
        if(link != n && arr[link + 1]) ll[rr[link + 1]] = link + 1;
        top --; arr[link] = false;
    }
}

void Solve( ) {
    
    int R, now = 1;
    for(int i = 1;i <= n;i += b) {
        now_ans = 1; int num = 0;
        while(now <= m && q[now].l >= i && q[now].l <= i + b - 1) Q[++ num] = q[now], now ++;
        if(! num) continue;
        idc ++; R = min(n, i + b - 1);
        sort(Q + 1,Q + num + 1, cmp_r);
        for(int j = 1;j <= num;j ++) {
            while(R < Q[j].r) work(a[++ R], false);
            int tmp = now_ans;
            for(int k = min(Q[j].r, min(n, i + b - 1));k >= Q[j].l; k --)
                work(a[k], true);
            ans[Q[j].id] = now_ans; 
            now_ans = tmp; restore( );
        }
    }
    for(int i = 1;i <= m;i ++) printf("%d\n", ans[i]);
}

int main( ) {
    
    freopen("ants.in","r",stdin);
    freopen("ants.out","w",stdout);
    Init( );
    Solve( );
}