洛谷P2144 bzoj1002 [FJOI2007]轮状病毒 (高精度板子)

P2144 [FJOI2007]轮状病毒

题目描述

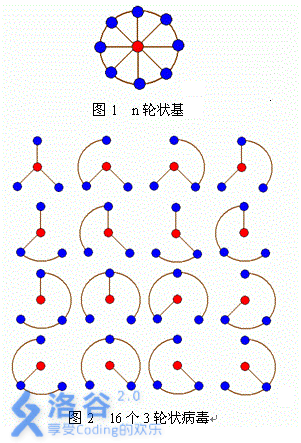
轮状病毒有很多变种。许多轮状病毒都是由一个轮状基产生。一个n轮状基由圆环上n个不同的基原子和圆心的一个核原子构成。2个原子之间的边表示这2个原子之间的信息通道，如图1。

n轮状病毒的产生规律是在n轮状基中删除若干边，使各原子之间有唯一一条信息通道。例如，共有16个不同的3轮状病毒，入图2所示。

给定n(N<=100)，编程计算有多少个不同的n轮状病毒。

输入输出格式

输入格式：

第一行有1个正整数n。

 

输出格式：

将编程计算出的不同的n轮状病毒数输出

输入输出样例

输入样例#1： 复制

3

输出样例#1： 复制

16

暴力打表找规律ye 暴力就是暴力并查集 把所有边存起来 $dfs$直到最后一条边 如果合法答案加$1$

发现当$n$分别为$1,2,3,4,5$时 答案分别为$1, 4, 16, 45, 121$ 

发现奇数项是平方数 偶数项是平方数减$4$

平方数是$1, 3, 4, 7, 11$ 类似于斐波那契数列 所以就高精度写一下就可以了(写这篇题解就是为了存高精度的板子qwq)

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e4 + 5;
int n;
struct Bigint {
    
    int size, num[N];
    void init(int data) {
        int s = 0;
        while(data) {
            s ++; num[s] = data % 10;
            data /= 10;
        }size = s;
    }
    void print( ) {
        for(int i = size;i >= 1;i --) printf("%d",num[i]);
        printf("\n");
    }
    void clear( ) {
        for(int i = 1;i <= size;i ++) num[i] = 0;
    }
}P, Q, D;

Bigint operator + (const Bigint & a, const Bigint & b) {
    
    Bigint ans; 
    ans.size = max(a.size, b.size) + 1;
    ans.clear( );
    for(int i = 1;i <= ans.size;i ++) {
        ans.num[i] = a.num[i] + b.num[i];
    }
    for(int i = 1;i < ans.size;i ++) {
        ans.num[i + 1] += ans.num[i] / 10;
        ans.num[i] %= 10;
    }
    while(! ans.num[ans.size]) ans.size --;
    return ans;
}

Bigint operator - (const Bigint & a, const Bigint & b) {
    
    Bigint ans; int s = max(a.size, b.size);
    ans.clear( );
    for(int i = 1;i <= s;i ++) {
        ans.num[i] = a.num[i] - b.num[i];
        if(ans.num[i] < 0) {
            ans.num[i + 1] --; ans.num[i] += 10;
        }
    }
    while(! ans.num[s]) s --; ans.size = s;
    return ans;
}

Bigint operator * (const Bigint & a, const Bigint & b) {
    
    Bigint ans; int s1 = a.size, s2 = b.size;
    int s = a.size + b.size - 1;
    ans.clear( );
    for(int i = 1;i <= s1;i ++)
        for(int j = 1;j <= s2;j ++)
            ans.num[i + j - 1] += a.num[i] * b.num[j];
    int k = 1;
    while(ans.num[k] || k <= s) {
        ans.num[k + 1] += ans.num[k] / 10;
        ans.num[k] %= 10;
        k ++;
    }
    while(ans.num[k] == 0) k --;
    ans.size = k;
    return ans;
}

int main( ) {
    
    scanf("%d",& n);
    P.init(1); Q.init(3); D.init(4);
    for(int i = 3;i <= n;i ++) {
        if(i % 2) P = P + Q;
        else Q = P + Q;
    }
    if(n % 2) {
        P = P * P; P.print( );
    }
    else {
        Q = Q * Q - D; Q.print( );
    }
}