18.10.7 考试总结
这道题还是很温柔的签到题 看了两分钟就搞出来了 然后忘记在每次更新队首之后重新更新答案了
然后幸好改出来惹
用滑动窗口维护对于每个右端点的最优左端点 就是每次加入元素 如果合法那么我就贪心的弹出队头然后区间长度取最小值即可
代码
#include <bits/stdc++.h> #define oo 1e9 using namespace std; const int N = 2 * 1e5 + 5; int T, a[N], n, k, r, b, q, cmd[N], num, len; int t[N]; void clear( ) { memset(t, 0, sizeof(t)); memset(cmd, 0, sizeof(cmd)); num = 0; } bool check(int pos) { if(t[a[pos]] - 1 >= cmd[a[pos]]) return true; return false; } void deal( ) { int tot = 0; int head = 0, tail = 0, las = 1; len = oo; for(int i = 1;i <= n;i ++) { tail ++; t[a[i]] ++; if(t[a[i]] == cmd[a[i]]) tot ++; while(check(las) && head < tail) { t[a[las]] -- ; las ++, head ++; } if(tot == num) len = min(len, i - las + 1); } } int read( ) { int t = 1, ans = 0; char x; x = getchar( ); while(x < '0' || x > '9') { if(x == '-') t = -1; x = getchar( ); } while(x >= '0' && x <= '9') { ans = ans * 10 + x - '0'; x = getchar( ); } return ans * t; } void Solve( ) { scanf("%d",& T); while(T --) { clear( ); n = read( ), k = read( ), r = read( ); for(int i = 1;i <= n;i ++) a[i] = read( ); for(int i = 1;i <= r;i ++) { b = read( ); q = read( ); cmd[b] = max(cmd[b], q); } for(int i = 0;i <= k;i ++) if(cmd[i] > 0) num ++; deal( ); if(len == oo) printf("DESTROY ALL\n"); else printf("%d\n", len); } } int main( ) { freopen("drop.in","r",stdin); freopen("drop.out","w",stdout); Solve( ); }
emmmmm考试的时候wans给我说这道题是2sat我还不信... 然后就被华丽丽的打脸饿
先复习一下这玩意儿吧 这个玩意儿是对于很多约束条件进行建边 $a -> b$表示选择了$a$就必须选择$b$
同一种东西有两种状态$a, -a$ 显然这两种状态是不能同时出现的 也就是说如果我沿着一种状态可以走到另一状态 那么这个条件就是不合法的
并且普通的$2sat$具有对称性 比如某个条件$(i, j)$表示$i, j$ 不能共存 也就是说连边$i -> -j,j -> -i$
所以对于2sat而言能从$i$走到$j$就一定能从$j$走到$i$ 也就是说他们在同一个强连通分量中 跑一遍$tarjan$ 在判断每个点的两个状态是否在同一个强连通分量就好了
那么对于这道题而言 题目条件$(i, j)$建边方式和上面的一样 所以也就是说这样子建图是尽可能保证不出现行星被炸掉的情况
所以我们的目的就转化成了添加若干条边 使某物品的两状态可以互相到达 由于对称性 我们只需要保证一个点能走到另一个点就可以了
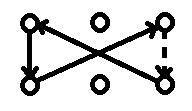假设上面的点表示正状态 下面负状态 那么我们建边只能从上面的点指向下面的点
对于这种上面的状态可以指向下面的状态而言 因为对称性 所以只要下面的点能够到上面 根据对称性 就只需要添加一条虚线边即可 直接到达自己显然不需要添加任何边
那么相反的 就只需要多添加自己的上面指向下面那条边就可以了
那么无解的情况就是下面的点没有一个能够到上面 也就是说走不通路的情况了 因为我们只能从上往下建边
枚举每个点 在这样子讨论一下跑跑dfs就可以了
代码
#include <bits/stdc++.h> using namespace std; const int N = 4000 + 5; int T, n, m, tot, head[N], nex[2 * N],tov[2 * N]; bool vis[N]; void add(int u, int v) { tot ++; nex[tot] = head[u]; tov[tot] = v; head[u] = tot; } int read( ) { int t = 1, ans = 0; char x; x = getchar( ); while(x < '0' || x > '9') { if(x == '-') t = -1; x = getchar( ); } while(x >= '0' && x <= '9') { ans = ans * 10 + x - '0'; x = getchar( ); } return t * ans; } void Add_Edge( ) { n = read( ),m = read( ); for(int i = 1;i <= m;i ++) { int x, y; x = read( ), y = read( ); int xx = x > 0 ? x + n : -x; int yy = y > 0 ? y + n : -y; if(x < 0) x = -x + n; if(y < 0) y = -y + n; add(x, yy); add(y, xx); } } void clear( ) { memset(head, 0, sizeof(head)); tot = 0; } void dfs(int u) { vis[u] = true; for(int i = head[u];i;i = nex[i]) { int v = tov[i]; if(! vis[v]) dfs(v); } } void Solve( ) { scanf("%d",& T); while(T --) { clear( ); Add_Edge( ); int ans = 3; for(int i = 1;i <= n;i ++) { memset(vis, 0, sizeof(vis)); dfs(i); int ret = 3; if(vis[i + n]) { memset(vis, 0, sizeof(vis)); dfs(i + n); if(vis[i]) {ans = 0; continue;} for(int j = 1;j <= n;j ++) if(vis[j]) { ret = 1; break; } } else { memset(vis, 0, sizeof(vis)); dfs(i + n); if(vis[i]) {ans = min(ans, 1); continue;} for(int j = 1;j <= n;j ++) if(vis[j]) { ret = 2; break; } } ans = min(ans, ret); } if(ans == 3) printf("No Way\n"); else printf("%d\n",ans); } } int main( ) { freopen("god.in","r",stdin); freopen("god.out","w",stdout); Solve( ); }
考试的时候$n$方暴力真的美滋滋还有60分
正解的思路其实和暴力是一样的 但是他用了无比优美的优化
暴力的思想大概是 贪心
先从左往右扫，如果某一时刻不满足要求，则需要删除前面中某一个支持对方的人。我们贪心地选择删除当前时刻访问的人（肯定是支持对方），然后继续往后扫。
然后再从右往左扫，作相同的操作。
直观地理解是这样的：我们尽量删除靠右的人，使得从右往左扫时少删除一些人。
可以采用交换论证法证明这贪心是对的。
我们可以把$C$看作$-1$，$V$看作$1$ 那么对于一段从右向左的区间而言 最小后缀和相反数就能表示杀掉人的个数 因为$C$越多 后缀和越小
题解写得好 我复制一波 在按照自己的理解修改一下
可以发现一个区间从左往右扫完，从右往左扫的这个过程可以不用实现出来。只需要求出剩下节点中从右端点开始的最小后缀和的相反数即可。
然后我们发现，如果两个询问区间拥有相同的左端点，则只需要作一次从左往右扫的工作。这使我们想到要离线化解决问题。
我们将询问按左端点排序，按照左端点从大到小的顺序求解询问。 至于每个区间的最小后缀和很容系想到用线段树维护
如果已知从$i$开始向右扫需要删除那些结点，则从$i - 1$开始向右扫需要删除那些结点可以快速求出 在进行修改的同时进行线段树的维护。
具体来说 如果$i-1$是支持者 则左数第一个被删除的结点与它抵消 相当于把他放了出来 也就是说他会在后续的后缀和中做出$-1$的贡献 注意后缀和指的是剩下的人和
如果$i - 1$是反对者 则加入被删除的结点里 他对线段树不作出贡献。
该过程可以用栈维护。
那么对于每个询问 可以在栈中二分得到从左往右的要杀的人的个数 在线段树中求最小后缀和 取相反数相加即可
总的来说 栈维护从左往右杀的人 线段树维护剩下的人从右往左杀的人
代码(这道题我竟然没看std改出来了hhh)
#include <bits/stdc++.h> using namespace std; const int N = 5 * 1e5 + 5; int a[N], q, sum[4 * N], f[4 * N], stk[N], top, n, ans[N]; char s[N]; struct event { int l, r, id; event(int l = 0, int r = 0, int id = 0): l(l), r(r), id(id) {} }b[N]; bool cmp(const event & a, const event & b) { return a.l < b.l; } void Init( ) { scanf("%d",& n); scanf("%s",s + 1); for(int i = 1;i <= n;i ++) a[i] = s[i] == 'C' ? 1 : -1; scanf("%d",& q); for(int i = 1;i <= q;i ++) { int l,r; scanf("%d%d",& l,& r); b[i] = event(l, r, i); } sort(b + 1, b + q + 1, cmp); } void update(int o) { sum[o] = sum[2 * o] + sum[2 * o + 1]; f[o] = min(f[2 * o + 1], sum[2 * o + 1] + f[2 * o]); } void modify(int o, int l, int r, int pos, int del) { if(l == r) { f[o] += del; sum[o] += del; return ; } int mid = l + r >> 1; if(pos <= mid) modify(2 * o, l, mid, pos, del); else modify(2 * o + 1, mid + 1, r, pos, del); update(o); } void init(int pos) { if(a[pos] == 1) { stk[++ top] = pos; //modify(1, 1, n, pos, -1); } else { modify(1, 1, n, pos, 1); if(top > 0) { modify(1, 1, n, stk[top --], -1); } } } bool check(int pos, int side) { return stk[pos] <= side; } int find_pos(int pos) { int l = 1,r = top,ans = top + 1; bool tag = false; while(l <= r) { int mid = l + r >> 1; if(check(mid, pos)) ans = mid, r = mid - 1; else l = mid + 1; } return ans; } event query(int o, int l, int r, int L, int R) { if(l >= L && r <= R) { return event(f[o], sum[o], 0); } int mid = l + r >> 1; if(R <= mid) return query(2 * o, l, mid, L, R); if(L > mid) return query(2 * o + 1, mid + 1, r, L, R); event q1 = query(2 * o, l, mid, L, R); event q2 = query(2 * o + 1, mid + 1, r, L, R); event q3; q3.l = min(q1.l + q2.r, q2.l); q3.r = q2.r + q1.r; return q3; } void Solve( ) { int now = q; for(int i = n;i >= 1;i --) { init(i);event aa = query(1, 1, n, 1, 11); while(i == b[now].l) { int num1 = find_pos(b[now].r); num1 = top - num1 + 1; event num2 = query(1, 1, n, b[now].l, b[now].r); int as = num1 + max(0, -num2.l); ans[b[now].id] = as; now --; } } for(int i = 1;i <= q;i ++) printf("%d\n",ans[i]); } int main( ) { freopen("sworder.in","r",stdin); freopen("sworder.out","w",stdout); Init( ); Solve( ); return 0; }
