洛谷 P3586 [POI2015]LOG
题目描述
维护一个长度为n的序列,一开始都是0,支持以下两种操作:1.U k a 将序列中第k个数修改为a。2.Z c s 在这个序列上,每次选出c个正数,并将它们都减去1,询问能否进行s次操作。每次询问独立,即每次询问不会对序列进行修改。
输入输出格式
输入格式:
第一行包含两个正整数n,m(1<=n,m<=1000000),分别表示序列长度和操作次数。接下来m行为m个操作,其中1<=k,c<=n,0<=a<=10^9,1<=s<=10^9。
输出格式:
包含若干行,对于每个Z询问,若可行,输出TAK,否则输出NIE。
输入输出样例
说明
维护一个长度为n的序列,一开始都是0,支持以下两种操作:
1.U k a 将序列中第k个数修改为a。
2.Z c s 在这个序列上,每次选出c个正数,并将它们都减去1,询问能否进行s次操作。
每次询问独立,即每次询问不会对序列进行修改。
这道题就是完全树状数组嘛
一开始看到这个玩意儿觉得就是建造一颗值域树状数组 然后再查询值大于等于$s$的个数
如果个数满足大于等于$c$ 那这个玩意儿就是合法的
但是这个时候也出现了问题 有可能我大于等于$s$的个数不大于$c$ 但是他仍然合法
比如$2 2 3 6 9$ 我要取出两个数 进行$9$次操作 按照之前的想法这个是不行的
但是在这种情况下它可以用多个不同的小数来补齐 那么什么时候才能算是合法的呢
考虑如果大于等于$s$的个数小于$c$该怎么办 假设大于等于$s$数的个数有$k$个
那么这个时候除去那$k$个数 剩余我们还需要减去$(c - k) * s$次 就用小于$s$的数的和与这个做比较
如果大于等于那这个就是合法的 所以还需要维护一颗求数字之和的树状数组
仔细想一下 这个为什么不会出现小数不够减的情况呢
因为有先决条件$sum < (c - k) * s$ 又因为不合法的数均是小于$s$ 所以不合法的数的个数一定大于$(c - k)$
所以我们一定能够选出$(c - k)$ 个数 然后用后面的小数补齐 使它一定够减 就像这样
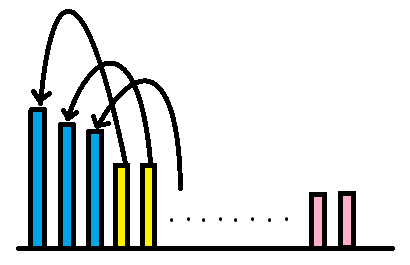
一定能够补齐 然后就各种操作搞一搞 要离散化
代码
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 2 * 1e6 + 5; int n,m,tot,t[N],b[N]; ll c[N],v[N]; struct option { int pd,x,y; }q[N >> 1],a[N >> 1]; void Init( ) { scanf("%d%d",& n,& m); for(int i = 1;i <= m;i ++) { char opt[5]; ll a,k; scanf("%s",opt); if(opt[0] == 'U') { scanf("%d%d",& a,& k); q[i].x = a; q[i].y = k; q[i].pd = 1; b[++ tot] = k; } else { scanf("%d%d",& a,& k); q[i].x = a,q[i].y = k; q[i].pd = 0; } } sort(b + 1,b + tot + 1); tot = unique(b + 1,b + tot + 1) - b - 1; } int lowbit(int a) { return a & (-a); } void modify(ll *c, int pos, ll del) { while(pos <= tot) { c[pos] += del; pos += lowbit(pos); } } ll query(ll *c,int pos) { ll ans = 0; while(pos >= 1) { ans += c[pos]; pos -= lowbit(pos); } return ans; } void Solve( ) { for(int i = 1;i <= m;i ++) { if(q[i].pd) { int pos1 = lower_bound(b + 1, b + tot + 1, t[q[i].x]) - b; int num = query(c, pos1) - query(c, pos1 - 1); if(num) modify(c, pos1, -1); if(num) modify(v, pos1, -t[q[i].x]); int pos2 = lower_bound(b + 1, b + tot + 1, q[i].y) - b; modify(c, pos2, 1); modify(v, pos2, q[i].y); t[q[i].x] = q[i].y; } else { int pos = lower_bound(b + 1, b + tot + 1, q[i].y) - b; int p = query(c, tot) - query(c, pos - 1); ll asum = query(v, tot),bsum = query(v, pos - 1); ll num = asum - bsum; if(p >= q[i].x) { printf("TAK\n"); continue; } else if(bsum >= 1ll * (q[i].x - p) * q[i].y) { printf("TAK\n"); continue; } else printf("NIE\n"); continue; } } } int main( ) { Init( ); Solve( ); }


