洛谷 P1852 [国家集训队]跳跳棋
题目描述
跳跳棋是在一条数轴上进行的。棋子只能摆在整点上。每个点不能摆超过一个棋子。
我们用跳跳棋来做一个简单的游戏:棋盘上有3颗棋子,分别在a,b,c这三个位置。我们要通过最少的跳动把他们的位置移动成x,y,z。(棋子是没有区别的)
跳动的规则很简单,任意选一颗棋子,对一颗中轴棋子跳动。跳动后两颗棋子距离不变。一次只允许跳过1颗棋子。
写一个程序,首先判断是否可以完成任务。如果可以,输出最少需要的跳动次数。
输入输出格式
输入格式:
第一行包含三个整数,表示当前棋子的位置a b c。(互不相同)
第二行包含三个整数,表示目标位置x y z。(互不相同)
输出格式:
如果无解,输出一行NO。
如果可以到达,第一行输出YES,第二行输出最少步数。
输入输出样例
说明
20% 输入整数的绝对值均不超过10
40% 输入整数的绝对值均不超过10000
100% 绝对值不超过10^9
这道题真的是一道好题!!是一道非常奇妙的建模题!!
题目上面有一句话是非常关键的 一次只允许跳过1颗棋子
这句话的意思也就是说对于三颗棋子$(a,b,c) (a < b < c)$
他可以两边棋子往中跳(两颗棋子到中间棋子的距离不一样是) 或者是中间棋子往两边跳
无论他是怎么跳 就相当于将这三者的某一段距离平移
很容易发现 对于每一个三元组$(a,b,c)$ 通过将两边的棋子不断的向中间跳 总能够到达一个状态使三者距离相等
而且这个状态是唯一的 因为都是往中间搞 相当于缩小边界 所以说每个状态对应只有一种跳法 也就是只对应了唯一一种最终情况
然后dalao们就联想到了树的父亲的唯一性 就可以将初始和过程中的状态当作子节点
将最终的 也就是两边无法往中间跳的状态看作根节点
但是一步一步跳显然会超时 所以联想到求$gcd$的方法 先上个图
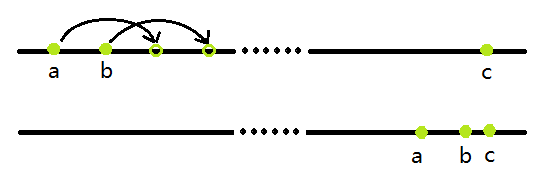
$a,b$ 最终跳到$c$ 相当于不断把$a,b$平移 平移到无法再平移为止
也就是说设原$a,b$距离$dis1 = b - a$ $b,c$距离$dis2 = c - b$ 假设$dis1 < dis2$
那么最终平移完了之后 得到的新$dis1$没变 而$dis2$变成了$dis2$ $mod$ $dis1$
要特判一下是否余数为$0$ 若为$0$则已经跳到根了
解决了跳的问题之后 现在要求三元组$(a,b,c)$转移到$(x,y,z)$的步数 也就是求这两个状态在树上的距离
就联想到了$lca$ 先判断这两个三元组的最终状态是否一致 如果一致 他们就是可以互相到达的 否则输出$NO$即可
然后现在考虑可以互相到达的情况 类比求$lca$的方法 先把他们调到一个深度 也就是他们分别到达根节点的步数做差 跳到他之后的这个状态
然后在二分他们到$lca$的距离 跳跳看他们的之后状态是否一致就可以了
代码
#include <bits/stdc++.h> #define oo 100000000 using namespace std; typedef long long ll; ll x,y,z,a,b,c; ll dep1,dep2,ans = 0; ll Get_root(ll a,ll b,ll c,ll & dep,ll & l) { ll d1 = b - a,d2 = c - b; while(d1 != d2) { if(d2 > d1) { ll s = d2 / d1,dis = d2 % d1; if(! dis) { dep += s - 1; l = d1; return a + (s - 1) * d1; } dep += s; a += s * d1; b += s * d1; d2 = dis; } else { ll s = d1 / d2,dis = d1 % d2; if(! dis) { dep += s - 1; l = d2; return a; } dep += s; b -= s * d2; c -= s * d2; d1 = dis; } } dep = 0; l = d1; return a; } void Swap(ll & a,ll & b,ll & c) { if(a > b) swap(a,b); if(a > c) swap(a,c); if(b > c) swap(b,c); } void Find_fa(ll & a,ll & b,ll & c,ll step) { while(step) { ll d1 = b - a,d2 = c - b; if(d2 > d1) { ll s = d2 / d1, dis = d2 % d1; if(s >= step) { a += step * d1; b += step * d1; return ; } a += s * d1; b += s * d1; step -= s; } else { ll s = d1 / d2,dis = d1 % d2; if(s >= step) { b -= step * d2; c -= step * d2; return ; } b -= s * d2; c -= s * d2; step -= s; } } } void Solve( ) { ll l = 0,r = min(dep2,dep1); ll st = oo; while(l <= r) { ll mid = l + r >> 1; ll aa = a,bb = b,cc = c; ll xx = x,yy = y,zz = z; Find_fa(aa,bb,cc,mid); Find_fa(xx,yy,zz,mid); if(aa == xx && bb == yy && cc == zz) st = mid,r = mid - 1; else l = mid + 1; } printf("%lld",ans + st * 2); } int main( ) { scanf("%lld%lld%lld%lld%lld%lld",& a,& b,& c,& x,& y,& z); Swap(a,b,c); Swap(x,y,z); ll del1,del2; ll pos1 = Get_root(a,b,c,dep1,del1); ll pos2 = Get_root(x,y,z,dep2,del2); if(del1 != del2 || pos1 != pos2) { printf("NO\n"); return 0; } printf("YES\n"); if(dep1 > dep2) { ans += dep1 - dep2; Find_fa(a,b,c,dep1 - dep2); } else if(dep2 > dep1) { ans += dep2 - dep1; Find_fa(x,y,z,dep2 - dep1); } Solve( ); }


