18.9.7 考试总结
啊今天是生日之后的第三天呢 然后我就大凶了.. 略微难受

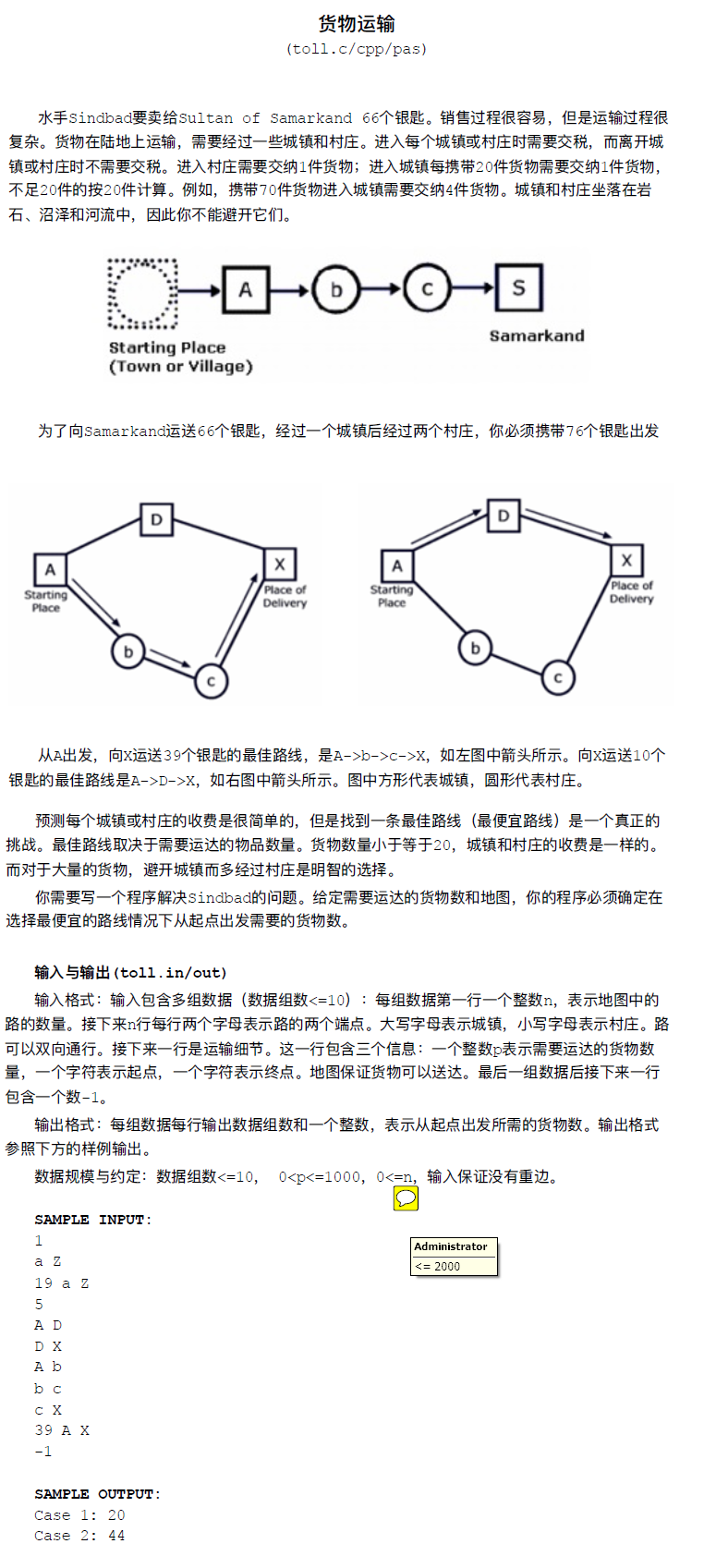
啊这道题正解是倒着搞得 ()然而蒟蒻我并不会... 于是就学习wans大佬的程序写的二分 + 正着搞得$Spfa$
$Spfa$最坏是 $nm$ 显然这道题是可以直接跑过的
所以对于起点二分一个最大货物量 然后$Spfa$跑每个点的最大值就可以了 按照题目意思来稿还是很清楚的
代码
#include <bits/stdc++.h> #define oo 10000000 using namespace std; const int N = 2000 + 5; int m,n,dis[N],head[N],nex[2 * N],tov[2 * N],p; int tot,s,t,cas; bool vis[N]; queue<int>Q; int deal(char c) { if(c >= 'a' && c <= 'z') return c - 'a'; else return c - 'A' + 26; } void add(int u, cint v) { tot ++; nex[tot] = head[u]; tov[tot] = v; head[u] = tot; } void add_Edge( ) { for(int i = 1;i <= n;i ++) { char a[2],b[2]; scanf("%s%s",a,b); int u = deal(a[0]),v = deal(b[0]); add(u,v); add(v,u); } } bool Spfa(int sum) { memset(dis,128,sizeof(dis)); memset(vis,0,sizeof(vis)); vis[s] = true; Q.push(s); dis[s] = sum; while(! Q.empty( )) { int u = Q.front( ); Q.pop( ); vis[u] = false; for(int i = head[u];i;i = nex[i]) { int v = tov[i]; if(v <= 25) { if(dis[v] < dis[u] - 1) { dis[v] = dis[u] - 1; if(! vis[v]) { vis[v] = true; Q.push(v); } } } else { if(dis[v] < dis[u] - (dis[u] + 19) / 20) { dis[v] = dis[u] - (dis[u] + 19) / 20; if(! vis[v]) { vis[v] = true; Q.push(v); } } } } } return dis[t] >= p; } void solve( ) { char a[2],b[2]; scanf("%d%s%s",& p,a,b); s = deal(a[0]),t = deal(b[0]); int l = p,r = oo,ans = oo; while(l <= r) { int mid = (l + r) >> 1; if(Spfa(mid)) ans = mid,r = mid - 1; else l = mid + 1; } printf("Case %d: %d\n",++ cas,ans); } int main( ) { freopen("toll.in","r",stdin); freopen("toll.out","w",stdout); while(scanf("%d",& n) != EOF) { if(n == -1) break; memset(head,0,sizeof(head)); tot = 0; add_Edge( ); solve( ); } }

emmmmmmm这道题我一来先把图搞出来 .... 搞出来.... 然后就不会了
谁来告诉我无向图最大点独立集咋跑...???? 然后意识到这是错误的
wans$SD$真的tqltql 我要膜dalao orzorzorz
可以发现 因为这是冒泡排序 所以每出现一个逆序对都要进行连边
也就是说如果他是单调递增的 那么就可以保证他们之间两两没有边 也就是说这是一个独立集
那么也就是我如果我们找到一个最长上升子序列 那么这就是新图里的最大点独立集
然后就$nlogn$跑就可以了 我用的线段树弄的 至于求这个的方法就不说了 网上到处都是
代码
#include <bits/stdc++.h> using namespace std; const int N = 1e5 + 5; int n,a[N],f[4 * N]; int query(int o,int l,int r,int L,int R) { if(l >= L && r <= R) { return f[o]; } int mid = (l + r) >> 1; int ans = 0; if(L <= mid) ans = max(ans,query(2 * o,l,mid,L,R)); if(mid < R) ans = max(ans,query(2 * o + 1,mid + 1,r,L,R)); return ans; } void update(int o) { f[o] = max(f[2 * o],f[2 * o + 1]); } void modify(int o,int l,int r,int pos,int val) { if(l == r) { f[o] = max(f[o],val); return ; } int mid = (l + r) >> 1; if(pos <= mid) modify(2 * o,l,mid,pos,val); else modify(2 * o + 1,mid + 1,r,pos,val); update(o); } void solve( ) { int ans = 0; for(int i = 1;i <= n;i ++) { int num = query(1,1,n,1,a[i]); modify(1,1,n,a[i],num + 1); ans = max(ans,num + 1); } printf("%d",ans); } int main( ) { freopen("sort.in","r",stdin); freopen("sort.out","w",stdout); scanf("%d",& n); for(int i = 1;i <= n;i ++) scanf("%d",& a[i]); solve( ); }

这道题一看数据范围就是状压dp啊 那么就愉快的乱写了... 我那个乱七八糟的程序竟然都还有60分...尴尬
总之垃圾程序就不说了 直接说正解吧 用 $01$ 状态表示哪些门选择了 哪些门没选择 而这个状态对应的钥匙数量是一定的
那么现在在钥匙一样多的情况下 我们要尽量使白色的钥匙更多 这是一个贪心的策略啊 使用多余的白色钥匙去补齐不够的钥匙
如果白钥匙一样多怎么办呢 比如我现在这个状态我可以有 $3,2,0$ 或者 $2,3,0$ 的钥匙 那么对应的能开的门就会出现问题
第一种就开不了 $2,3$ 第二种就开不了$3,2$ 但是我们并不知道开哪种门会更优 如果只记录白钥匙的情况
我们就只能傻乎乎的存下第一种达到$maxwhite$的情况 而对应的我们并不知道我们能够更新到哪种状态才是更优秀的
怎么办呢 就再开一维就好了 再存一个红钥匙的个数 就不会出现情况互相冲突的问题了
那么就很朴素的转移就好了 然后在转移的时候判断一下答案的最大值就可以了
代码
#include <bits/stdc++.h> using namespace std; const int N = 30; int n,red[N],gre[N],rk[N],wk[N],gk[N],k1,k2,k3,aans,ss; struct data { int r,w,g; int ans; }dp[(1 << 15)][151]; void Scanf( ) { scanf("%d",& n); for(int i = 1;i <= n;i ++) scanf("%d",& red[i]); for(int i = 1;i <= n;i ++) scanf("%d",& gre[i]); for(int i = 1;i <= n;i ++) scanf("%d",& rk[i]); for(int i = 1;i <= n;i ++) scanf("%d",& gk[i]); for(int i = 1;i <= n;i ++) scanf("%d",& wk[i]); scanf("%d%d%d",& k1,& k2,& k3); } int check(int pos,int nr,int ng,int nw) { if(red[pos] + gre[pos] > nr + ng + nw) return -1; if(nr >= red[pos]) { nr -= red[pos]; } else { int needw = red[pos] - nr; nw -= needw; if(nw < 0) return -1; nr = 0; } if(ng >= gre[pos]) { ng -= gre[pos]; } else { int needw = gre[pos] - ng; nw -= needw; if(nw < 0) return -1; ng = 0; } ss = nw; return nw + nr + ng; } void modify(int sta,int s,int num,int nr,int ng,int nw,int pos) { if(check(pos,nr,ng,nw) >= 0) { int cmp = check(pos,nr,ng,nw); cmp += rk[pos],cmp += gk[pos],cmp += wk[pos]; ss += wk[pos]; aans = max(aans,cmp); if((ss >= dp[sta][num].w) && (dp[s][num].w != -1)) { dp[sta][max(nr - red[pos],0) + rk[pos]].r = max(nr - red[pos],0) + rk[pos]; dp[sta][max(nr - red[pos],0) + rk[pos]].g = max(ng - gre[pos],0) + gk[pos]; dp[sta][max(nr - red[pos],0) + rk[pos]].w = ss; } } } void solve( ) { for(int sta = 0;sta < (1 << 14) - 1;sta ++) for(int i = 0;i <= 150;i ++) dp[sta][i].w = -1; dp[0][k1].r = k1, dp[0][k1].g = k2, dp[0][k1].w = k3; aans = k1 + k2 + k3; dp[0][k1].ans = aans; for(int sta = 0;sta < (1 << 14) - 1;sta ++) { int s = sta; for(int num = 0;num <= 150;num ++) { for(int j = 0;j < n;j ++) { if(!(sta & (1 << j))) { modify(sta | (1 << j),sta,num,dp[sta][num].r,dp[sta][num].g,dp[sta][num].w,j + 1); } } } } printf("%d",aans); } int main( ) { freopen("room.in","r",stdin); freopen("room.out","w",stdout); Scanf( ); solve( ); }
为什么总是在我最狼狈的时候出现呢。


