201971010235-阮凯 实验三 结对项目—《{0-1}KP 实例数据集算法实验平台》项目报告
| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | 2022年春软件工程课程班(2019级计算机科学与技术) |
| 这个作业要求链接 | 实验三 软件工程结对项目 |
| 我的课程学习目标 |
|
| 我实现的学习目标 |
|
| 结对方学号-姓名 | 201971010146-杨凯 |
| 结对方本次博客作业链接 | 201971010146-杨凯 实验三 结对项目—《{0-1}KP 实例数据集算法实验平台》项目报告 |
| 本项目Github的仓库链接地址 | 仓库连接 |
任务1的完成情况如下:
阅读《现代软件工程—构建之法》第3-4章内容,理解及掌握情况如下:
1. 代码风格规范:
- 主要是文字上的规定,其原则是:简明,易读,无二义性。
| 内容 | |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. 代码设计规范:
- 牵涉到程序设计、模块之间的关系、设计模式等方方面面的通用原则。
| 内容 | |
|---|---|
| 关于函数的重要原则是:只做一件事,并且要做好。 | |
| goto可以让函数有单一的出口。 | |
| 参数处理:所有参数都要验证其正确性。 断言:使用断言来验证参数的正确性。 |
3. 代码复审:
- 定义:看代码是否在代码规范的框架内正确的解决了问题。
- 形式:自我复审、同伴复审、团队复审。
- 目的:
- 找出代码的错误;
- 发现逻辑错误,程序可以编译通过,但是代码的逻辑是错的;
- 发现算法错误,比如使用的算法不够优化,边界条件没有处理好等;
- 发现潜在的错误和回归性错误-当前的修改导致以前修复的缺陷又重新出现;
- 发现可能需要改进的地方;
- 教育(互相教育)开发人员,传授经验,让更多的成员熟悉项目各部分的代码,同时熟悉和应用领域相关的实际知识。
- 代码复审的步骤:
- 代码必须成功地编译,在所有要求的平台上,同时要编译Debug|Retail 版本。
- 程序员必须测试过代码。
- 程序员必须提供新的代码,以及文件差异分析工具。
- 在面对面的复审中,一般是开发者控制流程,讲述修改的前因后果。但是复审者有权在任何时候打断叙述,提出自己的意见。
- 复审者必须逐一提供反馈意见。
- 开发者必须负责让所有的问题都得到满意的解释或解答,或者在TFS中创建新的工作项以确保这些问题会得到处理。
- 对于复审的结果,双方必须达成一致意见。
4. 结对编程:
- 在结对编程模式下,一对程序员肩并肩、平等地、互补地进行开发工作。
- 优点:
- 结对编程能提供更好的设计质量和代码质量。
- 对开发人员来说,结对编程可以带来更多的信心,高质量的产能带来更高的满足感。
- 在企业管理层次上,结对能更有效地交流,相互学习和传递经验,分享知识,能更好地应对人员流动。
- 若对结对编程运用得当,则可取得更高的投入产出比。
任务2的完成情况如下:
1. 结对方项目二博客链接:杨凯的博客
2. 结对方Github项目仓库链接:杨凯的Github仓库
3. 结对方项目二博客评论链接:对杨凯项目二博客评论
- 点评内容如下:
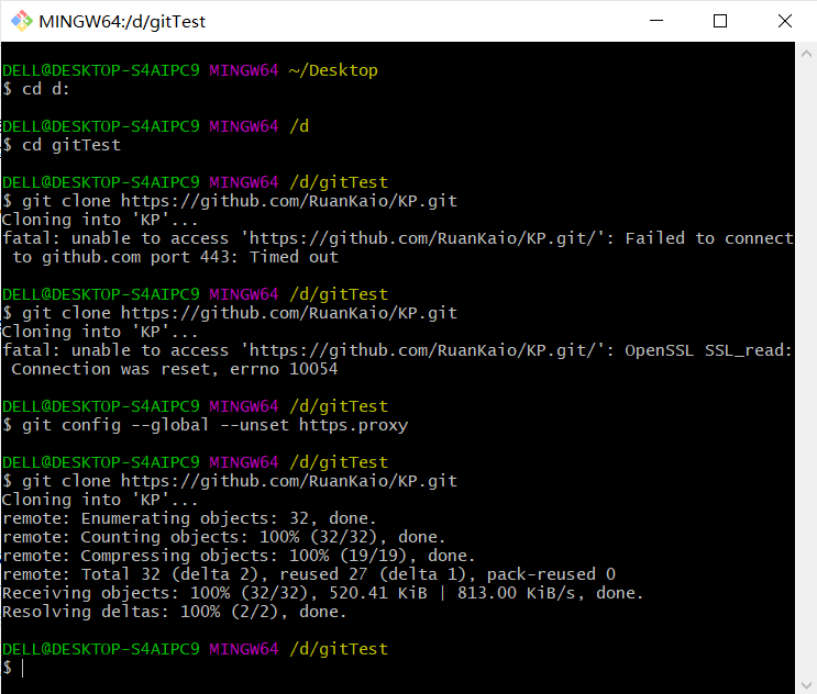
4. 克隆结对方项目源码:
- 在克隆的过程中,出现了错误,在查阅相关材料后,克隆成功,克隆情况如下所示:
- 运行结对方的代码,其运行结果和结对方在其博客中所描述的一致,仔细查看代码后,了解到结对方没有实现对一组{0-1}KP数据按重量比进行非递增排序,进行代码的修改后,帮其实现了此功能。
5. 代码核查表:
- 项目二的开发者:杨凯
- 项目二的复审者:阮凯
| 部分 | 要求 | 实际完成情况 |
|---|---|---|
1. 概要部分 |
1)代码符合需求和规格说明么? |
较符合; |
2)代码设计是否考虑周全? |
考虑的较为周全; | |
3)代码可读性如何? |
代码的可读性较好; | |
4)代码容易维护么? |
较易维护; | |
5)代码的每一行都执行并检查过了吗? |
多数执行并检查了,有少数并未执行; | |
| 2. 设计规范部分 | 1)设计是否遵从已知的设计模式或项目中常用的模式? |
遵从; |
2)有没有硬编码或字符串/数字等存在? |
没有; | |
3)代码有没有依赖于某一平台,是否会影响将来的移植(如Win32到 Win64 )? |
没有,不会影响移植; | |
4)开发者新写的代码能否用已有的 Library/SDK/Framework 中的功能实现?在本项目中是否存在类似的功能可以调用而不用全部重新实现? |
能,存在,有些代码可以调用; | |
5)有没有无用的代码可以清除? |
有; | |
| 3. 代码规范部分 | 1)修改的部分符合代码标准和风格么? |
基本符合; |
| 4. 具体代码部分 | 1)有没有对错误进行处理?对于调用的外部函数,是否检查了返回值或处理了异常? |
对相关错误进行了处理,没有异常; |
2)参数传递有无错误,字符串的长度是字节的长度还是字符(可能是单/双字节)的长度,是以 0 开始计数还是以 1 开始计数? |
没有错误,本项目不涉及字符串 ; | |
3)边界条件是如何处理的?switch语句的default分支是如何处理的?循环有没有可能出现死循环? |
对switch语句的default分支没有进行处理,没有出现死循环; | |
4)有没有使用断言(Assert)来保证我们认为不变的条件真的得到满足? |
没有; | |
5)对资源的利用,是在哪里申请,在哪里释放的?有无可能存在资源泄漏(内存、文件、各种GUI资源、数据库访问的连接,等等)?有没有优化的空间? |
对资源的利用,在最开始申请,在完成相关功能的计算后将其释放,没有资源泄露,没有优化空间; | |
6)数据结构中有没有用不到的元素? |
没有; | |
| 5. 效能 | 1)代码的效能(Performance)如何?最坏的情况是怎样的? |
基本完成了具体任务要求; |
2)代码中,特别是循环中是否有明显可优化的部分(C++中反复创建类,C# 中 string 的操作是否能用 StringBuilder 来优化)? |
没有; | |
3)对于系统和网络的调用是否会超时?如何处理? |
目前没有出现超时现象,若出现则将会进行杀毒处理,减少运行的进程,释放内存等; | |
| 6. 可读性 | 1)代码可读性如何?有没有足够的注释? |
可读性较好,注释较为全面; |
| 7. 可测试性 | 1)代码是否需要更新或创建新的单元测试?针对特定领域的开发(如数据库、网页、多线程等),可以整理专门的核查表。 |
代码需要更新; |
6. 结对方项目仓库中的日志数据:
- Fork:对结对方的仓库进行克隆。

- Clone:对结对方的仓库进行fork操作后,在自己的账号中会出现结对方的项目,之后就可以将其克隆到自己的电脑进行操作。
- Push:通过此命令可以将改动同步到自己的Github仓库中。
- Pull request:将已经修改的内容申请同步到结对方的项目中。
任务3的完成情况如下(项目必须包含src文件夹。):
1. 需求分析陈述:
Who 为谁设计,用户是谁?
0-1背包问题在现实中有着广泛的应用背景,如预算控制、项目选择、材料切割、货物装载等,用户是在相应的场景中需要拿到最优解得群体。
What 要解决那些问题?
需要解决如下问题:
- 读入数据:
- 可正确读入实验数据文件的有效{0-1}KP数据。
- 绘制散点图:
- 能够绘制任意一组{0-1}KP数据以价值重量为横轴、价值为纵轴的数据散点图。
- 非递增排序:
- 能够对一组{0-1}KP数据按重量比进行非递增排序。
- 最优解和求解时间:
- 用户能够自主选择:
- 贪心算法求解指定{0-1} KP数据的最优解和求解时间(以秒为单位)。
- 回溯算法求解指定{0-1} KP数据的最优解和求解时间(以秒为单位)。
- 动态规划算法求解指定{0-1} KP数据的最优解和求解时间(以秒为单位)。
- 用户能够自主选择:
- 数据保存:
- 任意一组{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
- 数据存储:
- {0-1}KP 实例数据集需存储在数据库。
- 平台:
- 平台可动态嵌入任何一个有效的{0-1}KP 实例求解算法,并保存算法实验日志数据。
- 界面:
- 人机交互界面要求为GUI界面(WEB页面、APP页面都可)。
- 遗传算法:
- 查阅资料,设计遗传算法求解{0-1}KP,并利用此算法测试平台。
Why 为什么解决这些问题?
解决这些问题可以加深对0-1背包问题所涉及的不同算法的理解。
2. 软件设计说明:
- 算法设计:
- 动态规划算法:在0-1背包问题中,物品i或者被装入背包,或者不被装入背包;wi表示物品的重量,vi表示对应的物品的价值,C表示背包的总容量,n表示物品的数量。
-
令V(i, j)表示在前i(1≤i≤n)个物品中能够装入容量为j(1≤j≤C)的背包中的物品的最大值,则可以得到如下动态规划函数:
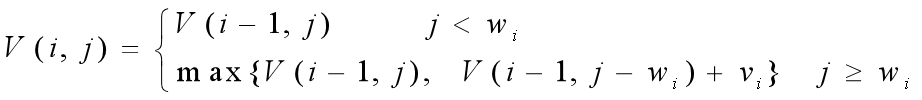
-
第一个式子表明:如果第i个物品的重量大于背包的容量,则物品i不能装入背包,则装入前i个物品得到的最大价值和装入前i-1个物品得到的最大价值是相同的。
-
二个式子表明:如果第i个物品的重量小于背包的容量,则会有以下两种情况:
- 如果第i个物品没有装入背包,则背包中物品的价值就等于把前i-1个物品装入容量为j的背包中所取得的价值。
- 如果把第i个物品装入背包,则背包中物品的价值等于把前i-1个物品装入容量为j-wi的背包中的价值加上第i个物品的价值vi;
- 取二者中价值较大者作为把前i个物品装入容量为j的背包中的最优解。
-
- 贪心算法:在每一步做出的选择都是当时看起来的最优选择,即局部最优选择。贪心算法解决0-1背包问题有三种策略,在此次项目设计中使用策略二。
- 策略一:每次装入的都是价值和重量比率最高的,也就是我们常说的性价比最高的;
- 策略二:每次装入的是当前可选择的东西中,价值最高的;
- 策略三:每次装入的是当前可选择东西中,重量最轻的。
- 回溯算法:在包含问题的所有可能解得解空间树中,从根结点出发,按照深度优先的策略进行搜索,对于解空间树的某个结点,如果该结点满足问题的约束条件,则进入该子树继续进行搜索,否则将以该结点为根结点的子树进行剪枝。
- 解空间:为n个元素所组成的集合的所有子集。
- 剪枝函数:用约束函数在扩展结点处减去不满足约束的子树,以及用限界函数减去得不到最优解得子树。
- 约束条件:装入背包的物品的总重量不得超过背包的容量。
- 遗传算法:是计算数学中用于解决最优化问题的搜索算法,是进化算法的一种。进化算法最初是借鉴了达尔文进化生物学中的一些现象而发展起来的,这些现象包括遗传、突变、自然选择以及杂交等。
- 编码:将问题空间转换为遗传空间;
- 生成初始种群:随机生成P个染色体;
- 种群适应度计算:按照确定的适应度函数,计算各个染色体的适应度;
- 选择:根据染色体适应度,按照选择算子进行染色体的选择;
- 交叉:按照交叉概率对被选择的染色体进行交叉操作,形成下一代种群;
- 突变:按照突变概率对下一代种群中的个体进行突变操作;
- 返回第3步继续迭代,直到满足终止条件。
- 动态规划算法:在0-1背包问题中,物品i或者被装入背包,或者不被装入背包;wi表示物品的重量,vi表示对应的物品的价值,C表示背包的总容量,n表示物品的数量。
- 代码设计:
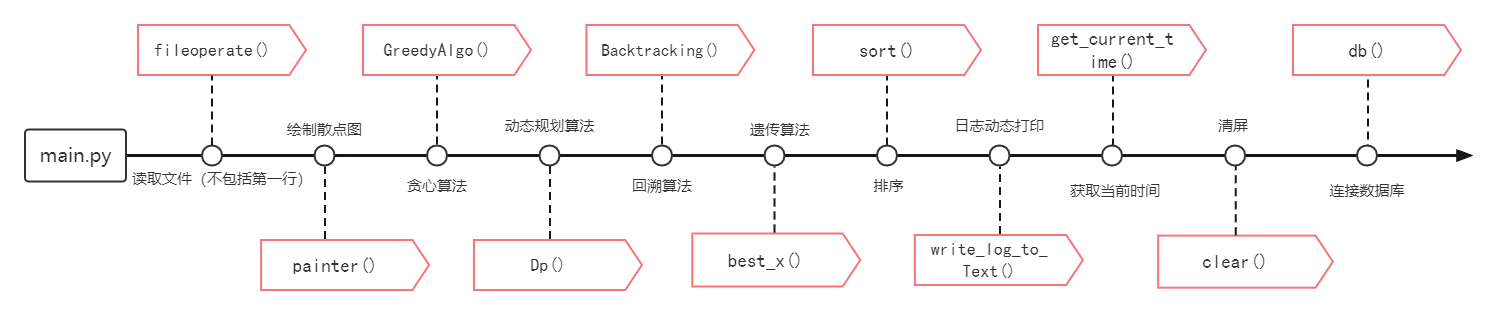
- main.py:
-
可正确读入实验数据文件的有效{0-1}KP数据;
-
用户可以自主选择数据文件;
-
用户能够自主选择贪心算法、动态规划算法、回溯算法、遗传算法求解指定{0-1} KP数据的最优解和求解时间(以秒为单位)。
-
任意一组{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件。
-
能够对任意一组{0-1}KP数据绘制以价值重量为横轴、价值为纵轴的数据散点图。
-
能够对任意一组{0-1}KP数据按重量比进行非递增排序。
-
平台可以动态嵌入任何一个有效的{0-1}KP 实例求解算法,并保存算法实验日志数据。
-
能够将任意一组{0-1}KP数据存入数据库。
-
人机交互界面是:通过python实现的GUI界面。
-
- resultD.txt:保存动态规划算法所求解的最优解和求解时间。
- resultG.txt:保存贪心算法所求解的最优解和求解时间。
- resultB.txt:保存回溯算法所求解的最优解和求解时间。
- resultR.txt:保存遗传算法所求解的最优解和求解时间。
- main.py:
3. 软件实现:
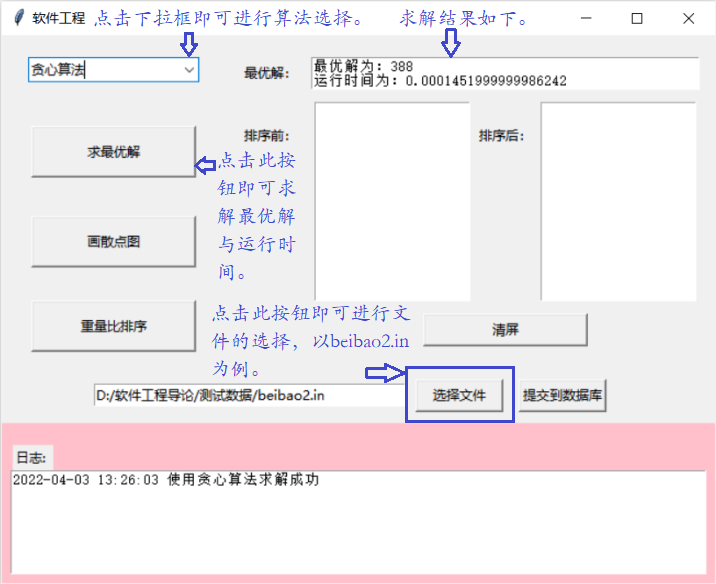
- 任意文件的选取以及贪心算法求解:
-
动态规划算法以及回溯算法的求解,与上面贪心算法的求解类似,在下拉框里选择相应的算法,之后点解“求最优解”按钮即可求解。
-
遗传算法求解、排序以及日志数据:
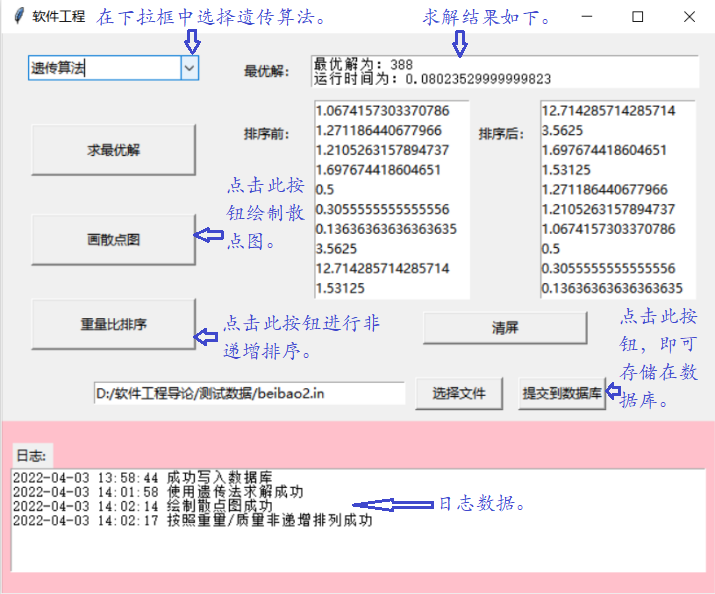
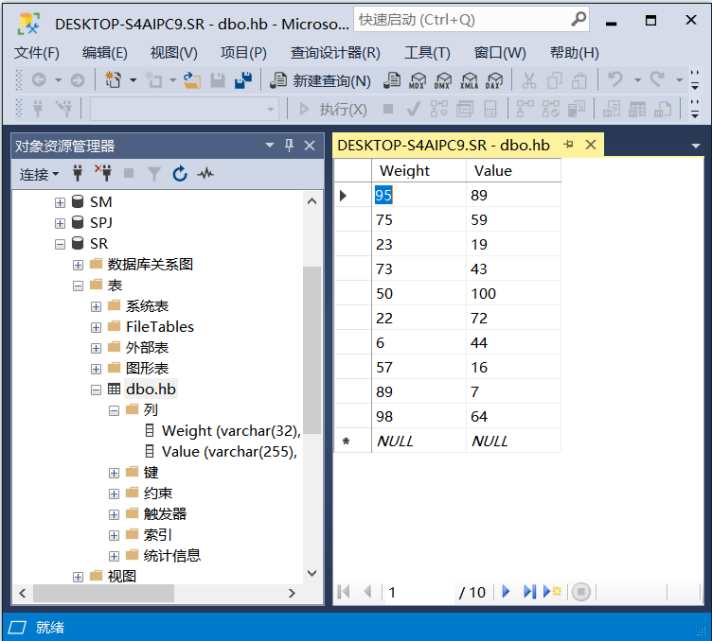
- 连接数据库,点击“提交到数据库”按钮即可将相应的文件存储在数据库:
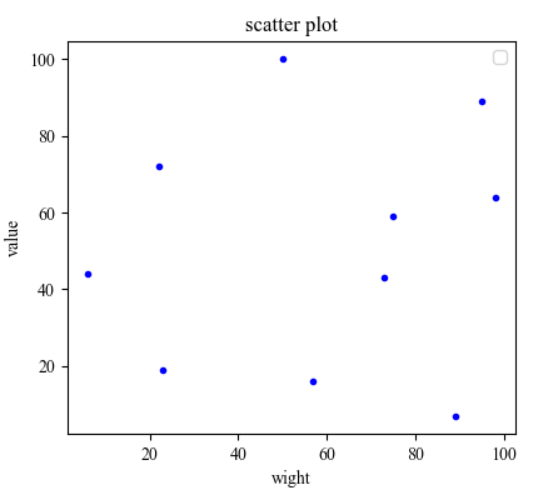
- 散点图的绘制情况如下图所示:
- 数据保存:

4. 代码展示:
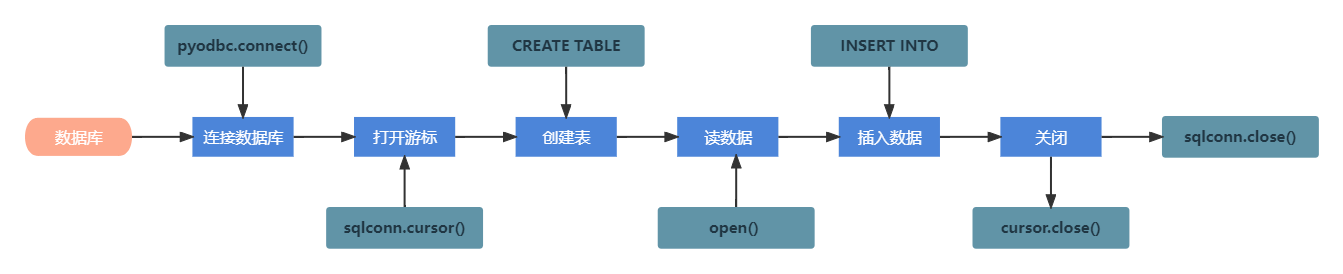
- 连接数据库:
sqlconn = pyodbc.connect(DRIVER='{ODBC Driver 17 for SQL Server}',
SERVER='DESKTOP-S4AIPC9',
DATABASE='SR',
Trusted_Connection='yes'
)
# 连接数据库
cursor = sqlconn.cursor() # 打开游标
cursor.execute("CREATE TABLE hb(\
Weight varchar(32) not null,\
Value varchar(255) not null,)\
") # 执行SQL语句
- 将读入的数据存入数据表中:
with open("测试数据/" + filename, 'r')as f:
datas = f.readlines()[1:] #第一行默认为总重量和数量,所以不读入。
for data in datas:
txt = re.split(r'[;,\s]\s*', data)
Weight = txt[0]
Value = txt[1]
cursor.execute("INSERT INTO hb(Weight,Value)VALUES('%s','%s')"%(Weight,Value))
# 调用insert方法
print("数据插入完成!")
- 非递增排序(在实验二的基础上进行了修改):
# 计算重量与价值的比值
for i in range(len(a)):
descending = []
F0 = int(a[i][0])
S0 = int(a[i][1])
T0 = F0 / S0
descending.append(T0)
print("非递增排序前为:")
print(descending)
descending.sort(reverse=True)
print("非递增排序后为:")
print(descending)
- 遗传算法:
#初始化,N为种群规模,n为染色体长度
def init(N,n):
C = []
for i in range(N):
c = []
for j in range(n):
a = np.random.randint(0,2)
c.append(a)
C.append(c)
return C
#评估函数
# x(i)取值为1表示被选中,取值为0表示未被选中
# w(i)表示各个分量的重量,v(i)表示各个分量的价值,w表示最大承受重量
def fitness(C,N,n,W,V,w):
S = []##用于存储被选中的下标
F = []## 用于存放当前该个体的最大价值
for i in range(N):
s = []
h = 0 # 重量
f = 0 # 价值
for j in range(n):
if C[i][j]==1:
if h+W[j]<=w:
h=h+W[j]
f = f+V[j]
s.append(j)
S.append(s)
F.append(f)
return S,F
#适应值函数,B位返回的种族的基因下标,y为返回的最大值
def best_x(F,S,N):
y = 0
x = 0
B = [0]*N
for i in range(N):
if y<F[i]:
x = i
y = F[x]
B = S[x]
return B,y
#计算比率
def rate(x):
p = [0] * len(x)
s = 0
for i in x:
s += i
for i in range(len(x)):
p[i] = x[i] / s
return p
#选择
def chose(p, X, m, n):
X1 = X
r = np.random.rand(m)
for i in range(m):
k = 0
for j in range(n):
k = k + p[j]
if r[i] <= k:
X1[i] = X[j]
break
return X1
#交配
def match(X, m, n, p):
r = np.random.rand(m)
k = [0] * m
for i in range(m):
if r[i] < p:
k[i] = 1
u = v = 0
k[0] = k[0] = 0
for i in range(m):
if k[i]:
if k[u] == 0:
u = i
elif k[v] == 0:
v = i
if k[u] and k[v]:
# print(u,v)
q = np.random.randint(n - 1)
# print(q)
for i in range(q + 1, n):
X[u][i], X[v][i] = X[v][i], X[u][i]
k[u] = 0
k[v] = 0
return X
#变异
def vari(X, m, n, p):
for i in range(m):
for j in range(n):
q = np.random.rand()
if q < p:
X[i][j] = np.random.randint(0,2)
return X
- 获取当前时间:
def get_current_time():
current_time = time.strftime('%Y-%m-%d %H:%M:%S', time.localtime(time.time()))
return current_time
- 清屏操作:
def clear():
LB1.delete(0, END)
LB2.delete(0, END)
- 日志动态打印:
def write_log_to_Text(logmsg):
global LOG_LINE_NUM
current_time = get_current_time()
logmsg_in = str(current_time) + " " + str(logmsg) + "\n" # 换行
if LOG_LINE_NUM <= 7:
log_txt.insert(END, logmsg_in)
LOG_LINE_NUM = LOG_LINE_NUM + 1
else:
log_txt.delete(1.0, 2.0)
log_txt.insert(END, logmsg_in)
- 列表框(用来排序的输出):
LB1 = Listbox(frameY)
LB2 = Listbox(frameY)
LB1.grid(row=1, column=1, pady=10, rowspan=3)
LB2.grid(row=1, column=3, pady=10, rowspan=3)
5. 程序运行:
程序运行时控制台的显示如下所示:
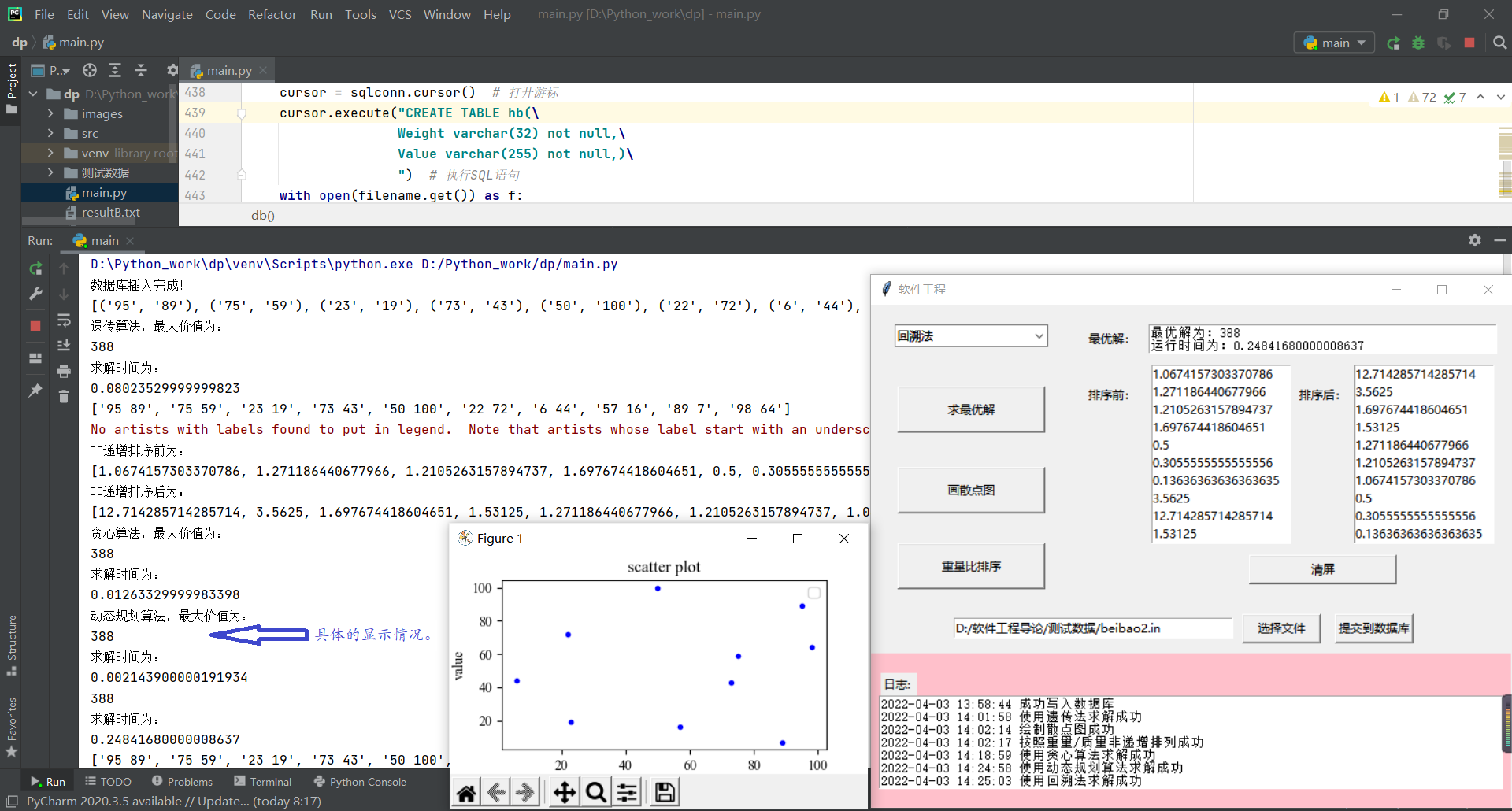
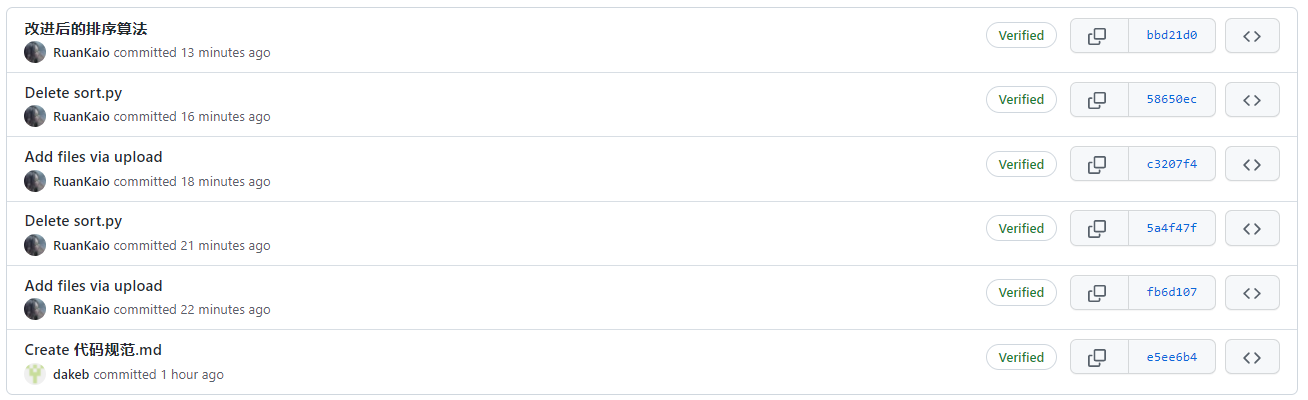
6. commit记录:
7. 结对照片:
8. 编码规范:
- 缩进:
- 缩进为4个空格(使用Tab键)。
- 行宽:
- 限定为100个字符。
- 常量:
- 常量命名全部大写,单词间用下划线隔开。
- 空行规则:
- 注释与其上面的代码用空行隔开;
- 在每个类声明后、每个函数定义结束之后都要加空行;
- 在一个函数体内,逻辑上密切相关的语句之间不加空行,其他地方应加空行分隔。
- 变量命名:
- 不以下划线或美元符号开始或结束;
- 不使用拼音与英文混合的方式;
- 方法名、参数名、成员变量、局部变量都使用lowerCamelCase(第一个词的首字母小写,以及后面每个词的首字母大写)风格,遵从驼峰形式。
- 每行最多字符数:
- 单行字符数限制不超过120个,超出需要换行,换行时遵循如下原则:
- 第二行相对第一行缩进 4个空格,从第三行开始,不再继续缩进;
- 运算符与下文一起换行;
- 方法调用的点符号与下文一起换行;
- 在多个参数超长,逗号后进行换行;
- 在括号前不换行。
- 单行字符数限制不超过120个,超出需要换行,换行时遵循如下原则:
- 函数命名:
- 函数名用大写字母开头的单词组合而成。
- 注释规则:
- 将复杂的注释放在函数头;
- 注释和代码同时更新,不用的注释删除;
- 注释与所描述内容进行同样的缩排;
- 注释掉的代码要配合相关说明;
- 操作符前后空格:
- 赋值运算符、逻辑运算符、加减乘除符号、三目运行符等二元操作符的左右必须加一个空格;
- 一元操作符前后不加空格;
- 中括号、点等这类操作符前后不加空格。
9. PSP展示:
(min) |
(min) |
||
|---|---|---|---|
| Planning | 计划 | ||
间,并规划大致工作步骤 |
|||
| Development | 开发 | ||
(包括学习新技术) |
|||
(和同事审核设计文档) |
|||
(为目前的开发制定合适的规范) |
|||
(自我测试。修改代码, 提交修改) |
|||
| Reporting | 报告 | ||
Process Improvement Plan |
10. 小结感受:
两人合作真的能够带来1+1>2的效果,在结对编程的过程中,需要进行有效的交流,在完成各自负责部分的情况下,对结对方的完成情况会进行检阅,提出不足之处,之后会加以改进,这样能够提供更好的设计质量和代码质量。


