201971010235-阮凯 实验二 软件工程个人项目 《0-1 背包问题》项目报告

项目 内容
课程班级博客链接 2022年春软件工程课程班(2019级计算机科学与技术)
这个作业要求链接 实验二 软件工程个人项目
我的课程学习目标
  • 掌握软件项目个人开发流程；
  • 掌握Github发布软件项目的操作方法。
我实现的学习目标
  • 掌握了个人项目的开发流程以及熟悉了求解{0-1}背包问题的各种算法；
  • 了解了使用python语言绘图以及排序以及掌握了Github发布软件项目的操作方法；
  • 了解了PSP的特点以及软件设计的原则。
项目Github的仓库链接地址 https://github.com/RuanKaio/dp

任务1的完成情况如下：

任务2的完成情况如下：

  • 《构建之法》第1章相关学习总结如下：

    • 程序=数据结构+算法、软件=程序+软件工程、软件企业=软件+商业模式。
    • 软件开发的阶段：玩具阶段、业余爱好阶段、探索阶段、成熟的产业阶段。
    • 软件工程：把系统的、有序的、可量化的方法应用到软件的开发、运营和维护上的过程。
    • 软件的特殊性：复杂性、不可见性、易变性、服从性、非连续性。
    • 软件工程与计算机科学的关系：计算机理论的进展会帮助软件工程，软件工程的进展会
      帮助计算机科学家更有效地进行实验和探索。
    • 软件工程的目标：创造“足够好”的软件。

  • 《构建之法》第2章相关学习总结如下：

    • 创建单元测试的主要步骤：
    1. 设置数据；
    2. 使用被测试类型的功能；
    3. 比较实际结果和预期结果。
    • 回归测试(Regression Test)的目的：
    1. 验证新的代码的确改正了缺陷；
    2. 同时要验证新的代码有没有破坏模块的现有功能，有没有Regression。
    • PSP：卡内基梅隆大学(CMU)的专家们针对软件工程师有一套模型，叫Personal Software Process(PSP)。
    • PSP的特点：
    1. 不局限于某一种软件技术，而是着眼于软件开发的流程；
    2. 不依赖于考试，主要靠工程师自己收集数据，然后分析，提高；
    3. 程序员的输入质量不高；
    4. PSP依赖于数据；
    5. PSP的目的是记录工程师如何实现需求的效率。
    • 软件设计的两个原则：
    1. 单一职责原则
    2. 封闭原则

任务3的完成情况如下：

1. 项目背景：

  背包问题（Knapsack Problem，KP）是NP Complete问题，也是一个经典的组合优化问题，有着广泛而重要的应用
背景。{０-1}背包问题（{0-1 }Knapsack Problem，{0-1}KP）是最基本的KP问题形式，它的一般描述为：从若干具有价值
系数与重量系数的物品（或项）中，选择若干个装入一个具有载重限制的背包，如何选择才能使装入物品的重量系数之和在
不超过背包载重前提下价值系数之和达到最大？

2. 需求分析：

  {0-1}KP数据集是研究{0-1}背包问题时，用于评测和观察设计算法性能的标准数据集；在此次实验中通过采用贪心算
法、动态规划算法、回溯算法求解{0-1}背包问题。

  • 贪心法是在每一步做出的选择都是当时看起来的最优选择，即局部最优选择。
  • 动态规划法是求解多阶段决策过程(decision process)最优化问题的数学方法。
  • 回溯法是在包含问题的所有可能解得解空间树中，从根结点出发，按照深度优先的策略进行搜索，对于解空间树的某
    个结点，如果该结点满足问题的约束条件，则进入该子树继续进行搜索，否则将以该结点为根结点的子树进行剪枝。

3. 功能设计：

  • 读入数据：
    • 可正确读入实验数据文件的有效{0-1}KP数据。
  • 绘制散点图：
    • 能够绘制任意一组{0-1}KP数据以价值重量为横轴、价值为纵轴的数据散点图。
  • 非递增排序：
    • 能够对一组{0-1}KP数据按重量比进行非递增排序。
  • 最优解和求解时间：
    • 用户能够自主选择贪心算法、动态规划算法、回溯算法求解指定{0-1} KP数据的最优解和求解时间（以秒为单位）。
  • 数据保存：
    • 任意一组{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。

4. 设计实现：

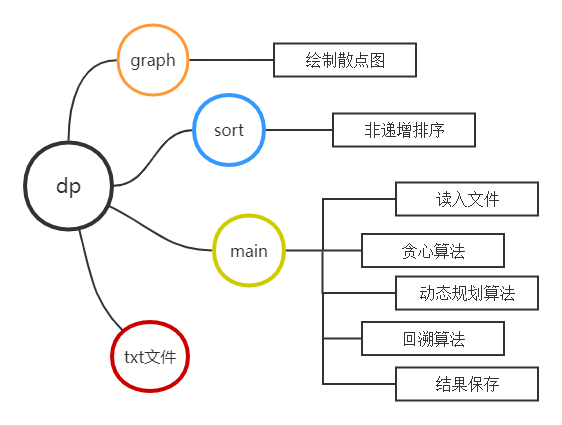
代码功能介绍如下：

  • graphy.py：能够绘制任意一组{0-1}KP数据以价值重量为横轴、价值为纵轴的数据散点图。
  • sort.py：能够对一组{0-1}KP数据按重量比进行非递增排序。
  • main.py：可正确读入实验数据文件的有效{0-1}KP数据，用户能够自主选择贪心算法、动态规划算法、回溯算法求解
    指定{0-1} KP数据的最优解和求解时间（以秒为单位），任意一组{0-1} KP数据的最优解、求解时间和解向量可保存为
    txt文件。
  • resultG.txt：保存贪心算法所求解的结果。
  • resultD.txt：保存动态规划算法所求解的结果。
  • resultB.txt：保存回溯算法所求解的结果。

5. 代码片段:

  • 散点图的绘制：
x, y = np.loadtxt(res, delimiter=' ', unpack=True)
plt.plot(x, y, '.', color='blue')

plt.xlabel('wight')
plt.ylabel('value')
plt.title('scatter plot')
plt.legend()
plt.show()
  • 从文件中读取数据：
# 读取数据(第一行读取)
f1 = open("D:\Python_work\dp\测试数据\\beibao0.in", "r")
a1 = []
res1 = f1.readlines()  # 若不想读取第一行则使用res = f.readlines()[1:]

for line in res1:
    line = line.replace('\n', '')  # 去掉\n;
    line = line.split(' ')  # 以空格划分
    a1.append(line)

f.close()
  • 贪心算法：
def GreedyAlgo(item,c,num):
    data = np.array(item)
    idex = np.lexsort([data[:,0], -1*data[:,1]])
    status = [0] * num
    Tw=0
    Tv=0

    for i in range(num):
        if data[idex[i],0] <= c:
            Tw += data[idex[i],0]
            Tv += data[idex[i],1]
            status[idex[i]] = 1
            c -= data[idex[i],0]
        else:
            continue

    print("贪心算法，最大价值为：")
    return Tv
  • 动态规划算法：
def Dp(w,v,c,num):
    cnt=[0 for j in range(c + 1)]

    for i in range(1,num+1):
        for j in range(c,0,-1):
                if j>=w[i-2]:
                    cnt[j] =max(cnt[j],cnt[j-w[i-2]]+v[i-2] )
                
    print("动态规划算法，最大价值为：")
    return cnt[c]
  • 回溯算法：
def Backtracking(k,c,num):
    global Nw,Nv,Bv,Bw
    status = [0 for i in range(num)]

    if k>=num:
        if Bv<Nv:
                Bv = Nv
    else:
        if Nw + w[k] <= c:
            status[k] = 1
            Nw += w[k]
            Nv += v[k]
            Backtracking(k+1,c,num)
            Nw -= w[k]
            Nv -= v[k]
        status[k] = 0
        Backtracking(k+1,c,num)
  • 结果保存：
result = "贪心算法：最优解：" + str(ret1) + "，" + "求解时间：" + str(time_sum)
file = open('D:\Python_work\dp\\resultG.txt', 'w')
file.write(result)
file.close()

6. 测试运行:

  • 散点图的绘制以beibao3.in为例：

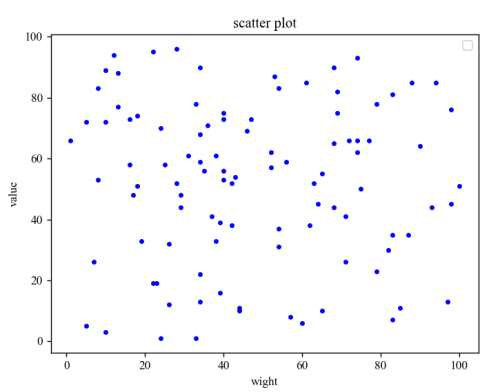
  • 非递增排序以beibao0.in为例：

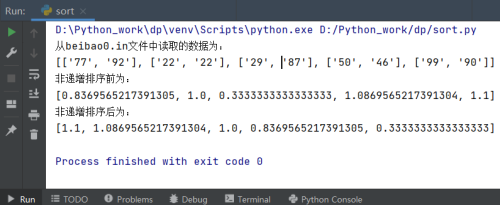
  • 用户自主选择贪心算法、动态规划算法、回溯算法进行求解以beibao0.in为例：

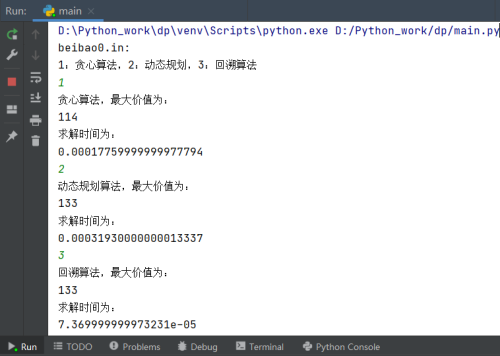
7. 代码规范：

  • 缩进：
    • 缩进为4个空格（使用Tab键）。
  • 变量命名：
    • 不以下划线或美元符号开始或结束；
    • 不使用拼音与英文混合的方式；
    • 方法名、参数名、成员变量、局部变量都使用lowerCamelCase(第一个词的首字母小写，
      以及后面每个词的首字母大写)风格，遵从驼峰形式。
  • 每行最多字符数：
    • 单行字符数限制不超过120个，超出需要换行，换行时遵循如下原则：
      • 第二行相对第一行缩进 4个空格，从第三行开始，不再继续缩进；
      • 运算符与下文一起换行；
      • 方法调用的点符号与下文一起换行；
      • 在多个参数超长，逗号后进行换行；
      • 在括号前不换行。
  • 函数最大行数：
    • 函数的规模尽量限制在100行以内。
  • 函数命名：
    • 函数名用大写字母开头的单词组合而成。
  • 类命名：
    • 使用UpperCamelCase(第一个词的首字母，以及后面每个词的首字母都大写)风格，遵从驼峰形式；
    • 抽象类命名使用Abstract或Base开头；
    • 异常类命名使用Exception结尾；
    • 测试类命名以它要测试的类的名称开始，以Test结尾。
  • 常量：
    • 常量命名全部大写，单词间用下划线隔开。
  • 空行规则：
    • 注释与其上面的代码用空行隔开；
    • 在每个类声明后、每个函数定义结束之后都要加空行；
    • 在一个函数体内，逻辑上密切相关的语句之间不加空行，其他地方应加空行分隔。
  • 注释规则：
    • 在源文件头部和函数头部进行注释；
    • 注释和代码同时更新，不用的注释删除；
    • 注释与所描述内容进行同样的缩排；
    • 注释掉的代码要配合相关说明；
    • 变量、常量、宏的注释应放在其上方相邻位置或右方。
  • 操作符前后空格：
    • 赋值运算符、逻辑运算符、加减乘除符号、三目运行符等二元操作符的左右必须加一个空格；
    • 一元操作符前后不加空格；
    • 中括号、点等这类操作符前后不加空格。

8. PSP展示:

PSP2.1
任务内容
计划共完成需要的时间
(min)
实际共完成需要的时间
(min)
Planning 计划
6
10
Estimate
估计这个任务需要多少时
间，并规划大致工作步骤
6
10
Development 开发
912
1336
Analysis
需求分析
(包括学习新技术)
16
26
Design Spec
生成设计文档
16
20
Design Review
设计复审
(和同事审核设计文档）
10
20
Coding Standard
代码规范
(为目前的开发制定合适的规范)
30
50
Design
具体设计
120
160
Coding
具体编码
480
720
Code Review
代码复审
120
160
Test
测试
(自我测试。修改代码, 提交修改)
120
180
Reporting 报告
70
92
Test Report
测试报告
30
36
Size Measurement
计算工作量
10
16
Postmortem &
Process Improvement Plan
事后总结,并提出过程改进计划
30
40

9. 经验分享：

在最开始了解此次作业时，认为自己一个人无法完成，然而结果是在自己长时间的努力下，完成了对自己来说完成不了的任务。

  • 起初最先想到是使用C++进行编程，为此做了如下准备：
    • 对上学期所学的算法设计课程进行了复习；
    • 查阅了如何读入文件；
    • 最终因对c++的掌握不全面，放弃了。
  • 之后想到的是使用java进行编程，为此做了如下准备：
    • 对以前所学过的相关知识进行了复习；
    • 对以前做过的实验进行了查看；
    • 最终因需要复习任务量太大而放弃。
  • 最后选择了python，但由于对其掌握也不是很全面，所以在代码的编写上耗费了大量的时间：
    • 对此次作业需要完成的功能，进行了查阅；
    • 进行散点图的绘制和非递增排序进行的较为顺利，在代码的编写过程中，报错较少；
    • 进行各种算法的编写时，各种错误信息层出不穷，写一步错一步，查找错误原因，修改；
    • 在编写代码的过程中，曾一度想要放弃，但是解决错误之后的喜悦，让我又有了继续编写下去的勇气；
    • 教训是“欠的账迟早要还”，“账”：对各种编程语言的掌握不全面；“还”：开始学习掌握一种适合自己的编程语言；
    • 收获是凡事尽量靠自己，自己动手，收获满满。
  • 经验是在以后的学习生活中，遇到难题时，不要一味的否定自己，坚持做下去，就会有不一样的收获。

任务4的完成情况如下：

已将项目提交至Github：

posted @ 2022-03-21 10:53  阮凯  阅读(144)  评论(3)  编辑  收藏  举报