基于投入导向的超效率CCR-DEA模型(MATLAB)
采用 CCR模型与超效率 DEA模型,在测算结果上完全相同;但对于效率项而言,每一个效率项都获得了一个全新且数值大于 1 的解。
基于投入导向的超效率CCR模型为:

借鉴参考文献[1],给出如下径向超效率代码。
clear
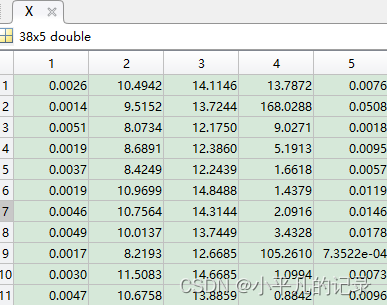
load('X');%投入指标数据,每一列代表每个决策单元的投入数据
load('Y');%产出指标数据。同上
x=X';y=Y';
n=size(x, 1); %决策单元数
m=size(x',1); %投入指标数
s=size(y',1); %产出指标数
epsilon=10^-10;%一个非常小的正数,在目标函数中用以识别松弛变量,并判断有效和弱有效
f=[zeros(1,n) -epsilon*ones(1,m+s) 1];%目标函数前n个决策变量的价值系数为0,第n+1到第n+m+s个决策变量的价值系数都为那个充分小的正数,第n+m+s+1个决策系数的价值系数为1
A=zeros(1,n+m+s+1);%不等式约束的系数矩阵,仅有1行,n+m+s+1列,元素全为0
b=0;%不等式约束左端的值,全部为0
LB=zeros(n+m+s+1,1);%决策变量的下限,共n+m+s+1行,1列。每个元素都为0,
UB=[];%决策变量的上限,无要求。
LB(n+m+s+1)=-inf;
for i=1:n
Aeq=[[x(:,1:i-1),zeros(m,1),x(:,i+1:n)] eye(m) zeros(m,s) -x(:,i)
[y(:,1:i-1),zeros(s,1),y(:,i+1:n)] zeros(s,m) -eye(s) zeros(s,1)];
beq=[zeros(m,1)
y(:,i)];
v(:,i)=linprog(f,A,b,Aeq,beq,LB,UB);
end
theta_se=v(n+m+s+1,:)';结果
0.0523743040732201
0.460194278564892
0.280835016622215
0.236269678021675
0.137840670422364
0.689863036524380
0.623629111454303
0.171727320159312
1.92741811023484
0.855787172666927
0.351011949617917
0.377780736929536
1.04518535254579
1.36798979340467
0.515844523360096
0.885503385809792
0.972765683802164
0.507884347300140
0.720737829252715
0.868254837493949
0.678868902578528
1.24654749293846
0.651339743186006
0.566628186204255
0.909258990279544
1.17729908354233
1.03973367345551
1.07081404510341
0.437828731291854
0.637403183592677
1.07791085587961
0.834316741706237
1.34902353413582
1.33482443066868
0.482137577192168
0.139365597368248
0.158433430063874
0.0478733732092864注:将投入指标数据保存在同个路径下,保存为X.mat文件,产出指标数据同样设置。
参考文献:[1]刘展,屈聪.MATLAB在超效率DEA模型中的应用[J].经济研究导刊,2014(03):86-87+93.
参考来源超效率DEA


 浙公网安备 33010602011771号
浙公网安备 33010602011771号