Python——Kmeans聚类算法、轮廓系数（算法理论、代码）
目录
3.4 使用for循环计算聚类个数为2至9时的轮廓系数值，寻找最优聚类个数
1 Kmeans模型理论
1.1 K-均值算法(K-means)算法概述
K-means算法是一种 无监督学习 方法，是最普及的聚类算法，算法使用 一个没有标签 的数据集，然后将数据聚类成不同的组。K-means算法具有一个迭代过程，在这个过程中，数据集被分组成若干个预定义的不重叠的聚类或子组，使簇的内部点尽可能相似，同时试图保持簇在不同的空间，它将数据点分配给簇，以便簇的质心和数据点之间的 平方距离之和最小 ，在这个位置，簇的质心是簇中数据点的算术平均值。
1.2 距离度量
闵可夫斯基距离(Minkowski distance)
$d(x,y)=(\sum_{i}|x_i -y_i|^p)^\frac{1}{p}$
𝑝取1或2时的闵氏距离是最为常用的𝑝 = 2 即为欧式距离𝑝 = 1 则为曼哈顿距离当𝑝取无穷时的极限情况下，可以得到切比雪夫距离
1.3 K-means算法流程
1：选择K个点作为初始质心。2：将每个点指派到最近的质心，形成K个簇。3：对于上一步聚类的结果，进行平均计算，得出该簇的新的聚类中心。4：重复上述两步/直到迭代结束：质心不发生变化。
首先，初始化称为簇质心的任意点。初始化时，必须注意簇的质心必须小于训练数据点的数目。因为该算法是一种迭代算法，接下来的两个步骤是迭代执行的。
初始化后，遍历所有数据点，计算所有质心与数据点之间的距离。现在，这些簇将根据与质心的最小距离而形成。在本例中，数据分为3 个簇 ( 𝐾 = 3 ) 。
第三步：移动质心，因为上面步骤中形成的簇 没有优化，所以需要形成优化的簇。为此，我 们需要迭代地将质心移动到一个新位置。取一个簇的数据点，计算它们的平均值，然后将该簇的质心移动到这个新位置。对所有其他簇重复相同的步骤。
初始化质心→簇赋值→迭代更新
——优化
上述两个步骤是迭代进行的，直到质心停止移动，即它们不再改变自己的位置，并且成为静态的。一旦这样做，k- 均值算法被称为收敛。K-均值的代价函数（又称 畸变函数 Distortion function）为：$J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_K )=\frac{1}{m}\sum_{i=1}^m||X^{(i)}-\mu_c(i)||^2$设训练集为： {𝑥 (1) , 𝑥 (2) , 𝑥 (3) , … , 𝑥 (𝑚) } ，簇划分𝐶 = {𝐶1, 𝐶2, ⋯ , 𝐶𝐾}，用𝜇1, 𝜇2 , . . . , 𝜇 𝐾 来表示聚类中心其中 𝜇 𝑐 (𝑖) 代表与 𝑥 (𝑖) 最近的聚类中心点。 我们的优化目标便是找出使得代价函数最小的 𝑐 (1) , 𝑐 (2) ,..., 𝑐 (𝑚) 和 𝜇 1 , 𝜇 2 , . . . , 𝜇 𝐾 。—— 优化过程记𝑘个簇中心为𝜇1 , 𝜇 2 , . . . , 𝜇 𝑘 ，每个簇的样本数目为𝑁1 , 𝑁 2 ,..., 𝑁 𝑘 使用平方误差作为目标函数:$J(\mu_1,...,\mu_K )=\frac{1}{2}\sum_{j=1}^K\sum_{i=1}^{N_j}(x_i-\mu_j)^2$
对关于从𝜇1 , 𝜇 2 , . . . , 𝜇 𝑘 ，的函数求偏导，这里的求偏导是对第𝑗个簇心𝜇𝑗求的偏导。故而其驻点为:现在，这个算法已经收敛，形成了清晰可见的不同簇。该算法可以根据簇在第一步中的初始化方式给出不同的结果。
1.4 K值的选择
现在我们需要找到簇的数量。通常通过“肘部法则”进行计算。我们可能会得到一条类似于人的肘部的曲线。下图中，代价函数的值会迅速下降，在𝐾 = 3的时候达到一个肘点。在此之后，代价函数的值会就下降得非常慢，所以，我们选择𝐾 = 3。这个方法叫“肘部法则” 。
K-均值 的一个问题在于，它有可能会停留在一个局部最小值处，而这取决于初始化的情况。为了解决这个问题，我们通常需要多次运行 K-均值 算法，每一次都重新进行随机初始化，最后再比较多次运行K-均值 的结果，选择代价函数最小的结果。
1.5 K-means的优点
鲁棒性高；速度快、易于理解、效率高；计算成本低、灵活性高；如果数据集是不同的，则结果更好；可以产生更紧密的簇；重新计算质心时，簇会发生变化。
1.6 K-means的缺点
需要预先指定簇的数量； 如果有两个高度重叠的数据，那么它就不能被区分，也不能判断有两个簇； 欧几里德距离可以不平等的权重因素，限制了能处理的数据变量的类型； 有时随机选择质心并不能带来理想的结果；无法处理异常值和噪声数据； 不适用于非线性数据集； 对特征尺度敏感；如果遇到非常大的数据集，那么计算机可能会崩溃。
1.7 聚类的评价指标
(1). 均一性：𝑝
类似于精确率，一个簇中只包含一个类别的样本，则满足均一性。其实也可以认为就是正确率(每个聚簇中正确分类的样本数占该聚簇总样本数的比例和)
(2). 完整性：𝑟
类似于召回率 ，同类别样本被归类到相同簇中，则满足完整性;(每个聚簇中正确分类的样本数占该类型的总样本数比例的和)
(3). V-measure:
均一性和完整性的加权平均
(4). 轮廓系数样本𝑖的轮廓系数：
簇内不相似度：计算样本i到同簇其它样本的平均距离为𝑎(𝑖)，应尽可能小。
簇间不相似度：计算样本𝑖到其它簇$C_j$的所有样本的平均距离$b_{ij}$，应尽可能大。
轮廓系数𝑠(𝑖)值越接近1表示样本𝑖聚类越合理，越接近-1，表示样本𝑖应该分类到另外的簇中，近似为0，表 示样本𝑖 应该在边界上;所有样本的𝑠(𝑖)的均值被成为聚类结果的轮廓系数。
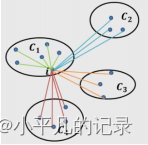
假设数据集被拆分为4个簇，样本𝑖对应的 𝑎(𝑖) 值就是所有𝐶1 中其他样本点与样本𝑖的距离平均值; 样本对应的𝑏(𝑖)值分两步计算，首先计算该点分别到𝐶2 、𝐶3和𝐶 4 中 样本点的平均距离，然后将三个平均值中的最小值作为𝑏(𝑖)的度量。
(5).调整兰德系数(ARI, Adjusted Rnd Index)数据集𝑆共有𝑁个元素， 两个聚类结果分别是：𝑋 和 𝑌 的元素个数为：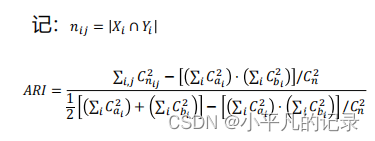
ARI取值范围为[−1,1]，值越大意味着聚类结果与真实情况越吻合。从广义的角度来讲，ARI衡量的是两个数据分布的吻合程度。
2 代码解释
from sklearn.cluster import KMeansKMeans传参详解：
- n_clusters : k值，聚类中心数量（开始时需要产生的聚类中心数量），默认为8
- max_iter : 算法运行的最大迭代次数，默认300，凸数据集不用管这个数，凹数据集需要指定。
- tol: 容忍的最小误差，当误差小于tol就会退出迭代（算法中会依赖数据本身），默认为1e-4
- n_init : （用不同的初始化之心运行计算的次数）k-means算法会随机运行n_init次，最终的结果将是最好的一个聚类结果，默认10
- init : 即初始值（质心）选择的方式，有三个选择
优化过的'k-means++', ，一般默认'k-means++' ，
完全随机选择'random': 随机选择k个实例作为聚类中心
自己指定的初始化质心，ndarray：如果传入为矩阵（ndarray），则将该矩阵中的每一行作为聚类中心
初始化过程如下：
从输入的数据点集合（要求有k个聚类）中随机选择一个点作为第一个聚类中心；（2）、对于数据集中的每一个点x，计算它与最近聚类中心(指已选择的聚类中心)的距离D(x)；（3）、选择一个新的数据点作为新的聚类中心，选择的原则是：D(x)较大的点，被选取作为聚类中心的概率较大；（4）、重复2和3直到k个聚类中心被选出来
- algorithm :可选的K-means距离计算算法， 可选{"auto", "full" or "elkan",default="auto"}
"full"：传统的距离计算方式.，支持稀疏数据。
"elkan"：使用三角不等式，效率更高，但是目前不支持稀疏数据。1、计算任意两个聚类中心的距离；2当计算x点应该属于哪个聚类中心时，当发现2*S(x，K1)<S（x，K2）时，根据三角不等式，S（x，K2）>S(x，K1)，
"auto"：当为稀疏矩阵时，采用full，否则elkan。
- precompute_distances : 是否将数据全部放入内存计算，可选{'auto', True, False}，开启时速度更快但是更耗内存。
'auto' : 当n_samples * n_clusters > 12million，不放入内存，否则放入内存，double精度下大概要多用100M的内存
True : 进行预计算
False : 不进行预计算
- n_jobs : 同时进行计算的核数（并发数），n_jobs用于并行计算每个n_init，如果设置为-1，使用所有CPU，若果设置为1，不并行，也可以自定义个数
- random_state : 用于随机产生中心的随机序列,指定确切的数字后，可以让每次运行程序，产生的结果都一样
- verbose : 是否输出详细信息，默认为0，值越大，细节打印越多。
● int：冗长度★ 0：不输出训练过程● 1：偶尔输出● >1：对每个子模型都输出
- copy_x : 是否直接在原矩阵上进行计算。默认为True，会copy一份进行计算。
新建对象后，常用的方法包括fit、predict、cluster_centers_和labels。fit（X）函数对数据X进行聚类，使用predict方法进行新数据类别的预测，使用cluster_centers_获取聚类中心，使用labels_获取训练数据所属的类别，inertia_获取每个点到聚类中心的距离和。
3 实操
附件wine数据集包含3种不同的葡萄酒的记录共178条。其中，每个特征对应葡萄酒的每种化学成分，并且都属于连续型数据。通过对wine数据集的数据进行聚类，实现葡萄酒的类别划分。 请依据wine数据集，编写Python代码完成下列操作：
（1）读取数据文件wine.csv，并储存为数据框wine。
（2）构建聚类数目为3的KMeans模型，并命名为kmeans。
（3）在数据框wine中添加一列 “label”,将各个样本的聚类标签对应填入“label”列中。
（4）根据计算出的聚类标签绘制各类别数量占比饼图。
（5）求取聚类结果的轮廓系数值（轮廓系数值是聚类结果的一种评价指标，其计算不需要真实标签）。
（6）使用for循环计算聚类个数为2至9时的轮廓系数值，寻找最优聚类个数。 交付结果文件和代码文件。
——数据集
3.1 构建聚类数目为3的KMeans模型
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3) #设定超参数聚类数为3
y_predicted = km.fit_predict(wine) #拟合+预测
y_predicted
wine['label'] = y_predicted #存储数据array([0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 2,
0, 0, 2, 2, 0, 0, 2, 0, 0, 0, 0, 0, 0, 2, 2, 0, 0, 2, 2, 0, 0, 2,
2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2, 1, 2, 1, 1, 2,
1, 1, 2, 2, 2, 1, 1, 0, 2, 1, 1, 1, 2, 1, 1, 2, 2, 1, 1, 1, 1, 1,
2, 2, 1, 1, 1, 1, 1, 2, 2, 1, 2, 1, 2, 1, 1, 1, 2, 1, 1, 1, 1, 2,
1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 2, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 1,
1, 2, 2, 2, 2, 1, 1, 1, 2, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 1, 1, 2,
2, 2, 1, 2, 2, 2, 1, 2, 1, 2, 2, 1, 2, 2, 2, 2, 1, 1, 2, 2, 2, 2,
2, 1])3.2 占比饼图
r1 = pd.Series(kmeans.labels_).value_counts() #统计各个类别的数目
r2 = pd.DataFrame(kmeans.cluster_centers_) #找出聚类中心
import matplotlib.pyplot as plt
label = ['0', '1', '2']
plt.pie(wine1['label'],labels = label, autopct='%.2f%%')
plt.show()
3.3 轮廓系数值
sklearn.metrics.silhouette_samples(wine, labels)
3.4 使用for循环计算聚类个数为2至9时的轮廓系数值，寻找最优聚类个数
from sklearn.metrics import silhouette_score
K=range(2,10)
score=[]
for k in K:
kmeans=KMeans(n_clusters=k)
kmeans.fit(wine)
score.append(silhouette_score(wine,kmeans.labels_,metric='euclidean'))
plt.plot(K,score,'r*-')
plt.xlabel('k')
plt.ylabel(u'轮廓系数')
plt.title(u'轮廓系数确定最佳的K值')Text(0.5, 1.0, '轮廓系数确定最佳的K值')
当k=3之后，在增加聚类的类别效果提高不是十分明显，由此可以确认此批数据的k应该取3.
