R——《时间序列分析——基于R》第5章 无季节效应的非平稳序列分析 习题1
目录
1.我国1949-2008年每年铁路货运量数据如表5-2所示。
| year | volume | year | volume | year | volume |
| 1949 | 5589 | 1969 | 53120 | 1989 | 151489 |
| 1950 | 9983 | 1970 | 68132 | 1990 | 150681 |
| 1951 | 11083 | 1971 | 76471 | 1991 | 152893 |
| 1952 | 13217 | 1972 | 80873 | 1992 | 157627 |
| 1953 | 16131 | 1973 | 83111 | 1993 | 162794 |
| 1954 | 19288 | 1974 | 78772 | 1994 | 163216 |
| 1955 | 19376 | 1975 | 88955 | 1995 | 165982 |
| 1956 | 24605 | 1976 | 84066 | 1996 | 171024 |
| 1957 | 27421 | 1977 | 95309 | 1997 | 172149 |
| 1958 | 38109 | 1978 | 110119 | 1998 | 164309 |
| 1959 | 54410 | 1979 | 111893 | 1999 | 167554 |
| 1960 | 67219 | 1980 | 111279 | 2000 | 178581 |
| 1961 | 44988 | 1981 | 107673 | 2001 | 193189 |
| 1962 | 35261 | 1982 | 113495 | 2002 | 204956 |
| 1963 | 36418 | 1983 | 118784 | 2003 | 224248 |
| 1964 | 41786 | 1984 | 124074 | 2004 | 249017 |
| 1965 | 49100 | 1985 | 130709 | 2005 | 269296 |
| 1966 | 54951 | 1986 | 135635 | 2006 | 288224 |
| 1967 | 43089 | 1987 | 140653 | 2007 | 314237 |
| 1968 | 42095 | 1988 | 144948 | 2008 | 330354 |
请选择适当的模型拟合该序列,并预测2009-2013年我国铁路货运量。
1.导入数据并绘图
library(aTSA)
test=read.csv("D:/时间序列/习题数据(基于R,EXCEL格式)/E5_1.csv")
y=ts(test$volume,start = 1949)
x=window(y,start=1949,end=2003)
plot(x,type="o")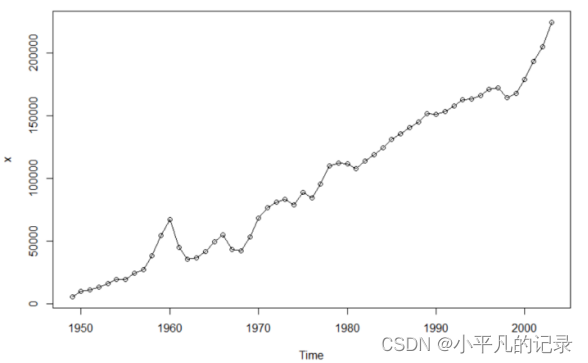
2.进行一阶差分并绘制该序列时序图
dif_x<-diff(x,type="o")
plot(dif_x,type="o")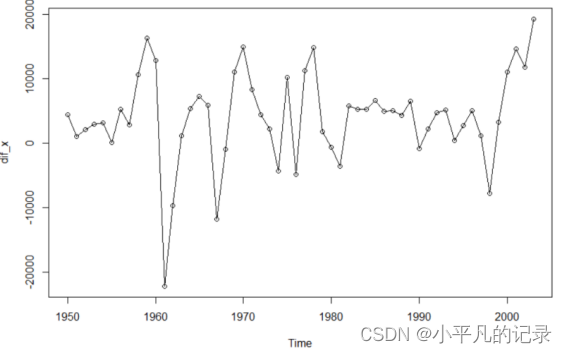
3.判断该序列的平稳性与纯随机性
adf.test(dif_x)
for(k in 1:2) print(Box.test(dif_x,lag = 6*k))——平稳性
Augmented Dickey-Fuller Test
alternative: stationary
Type 1: no drift no trend
lag ADF p.value
[1,] 0 -4.05 0.0100
[2,] 1 -3.79 0.0100
[3,] 2 -3.02 0.0100
[4,] 3 -2.05 0.0416
Type 2: with drift no trend
lag ADF p.value
[1,] 0 -5.03 0.01
[2,] 1 -5.24 0.01
[3,] 2 -4.87 0.01
[4,] 3 -4.12 0.01
Type 3: with drift and trend
lag ADF p.value
[1,] 0 -5.12 0.01
[2,] 1 -5.35 0.01
[3,] 2 -4.99 0.01
[4,] 3 -4.24 0.01
----
Note: in fact, p.value = 0.01 means p.value <= 0.01
ADF检验统计量的P值小于显著性水平(0.05),认为该序列为平稳序列
——纯随机性
Box-Pierce test
data: dif_x
X-squared = 14.384, df = 6, p-value = 0.02563
Box-Pierce test
data: dif_x
X-squared = 17.866, df = 12, p-value = 0.1198
6阶延迟的LB统计量的P值小于显著性水平5%,可判断该序列为非白噪声序列
4.考察该序列的自相关系数和偏自相关系数的性质
par(mfrow=c(1,2))
acf(dif_x)
pacf(dif_x)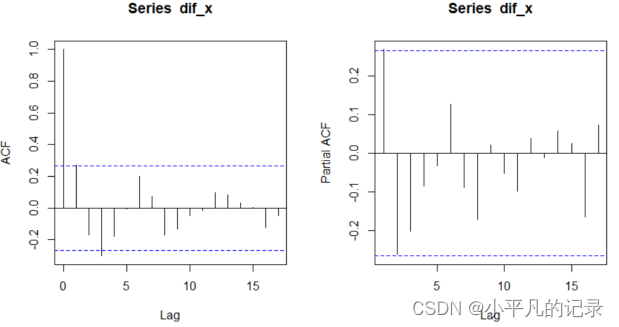
自相关系数图:呈有规律的衰减;偏自相关系数1阶截尾。选取ARIMA(1,1,0)和ARIMA(0,1,1)
5.选择适当模型拟合该序列的发展
5.1. ARIMA(1,1,0)不带漂移项
fit1<-arima(x,order=c(1,1,0),method = "ML")
fit1
ts.diag(fit1)Call:
arima(x = x, order = c(1, 1, 0), method = "ML")
Coefficients:
ar1
0.4643
s.e. 0.1266
sigma^2 estimated as 54343681: log likelihood = -557.64, aic = 1119.27
参数检验:参数$\phi _1$的估计值大于它的两倍标准差,参数显著
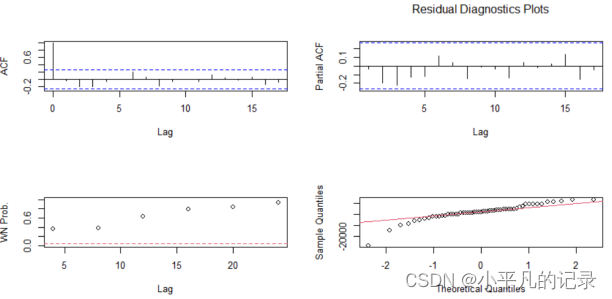
图 4 无漂移项模型显著性检验图
可看出各阶延迟下白噪声检验统计量的P值都显著大于0.05,可认为拟合模型的残差序列属于白噪声序列,该拟合模型显著成立。
5.2. ARIMA(1,1,0)带漂移项
library(forecast)
fit2<-Arima(x,order=c(1,1,0),include.drift = T)
fit2
tsdiag(fit2)Series: x
ARIMA(1,1,0) with drift
Coefficients:
ar1 drift
0.2883 4164.431
s.e. 0.1349 1310.414
sigma^2 = 49350270: log likelihood = -553.94
AIC=1113.87 AICc=1114.35 BIC=1119.84

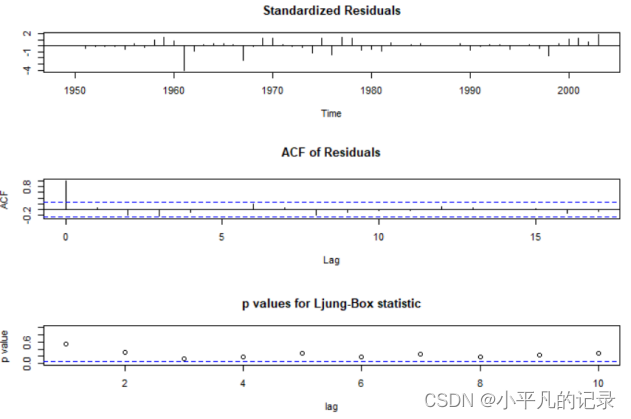
图 5 有漂移项模型显著性检验图
看出各阶延迟下白噪声检验统计量的P值都显著大于0.05,可认为拟合模型的残差序列属于白噪声序列,该拟合模型显著成立。
参数检验:参数$\phi _1$的估计值大于它的两倍标准差,参数显著;参数的估计值大于它的两倍标准差,参数显著。
5.3. ARIMA(0,1,1)不带漂移项
fit3<-arima(x,order=c(0,1,1),method = "ML")
fit3
ts.diag(fit3)Call:
arima(x = x, order = c(0, 1, 1), method = "ML")
Coefficients:
ma1
0.4374
s.e. 0.1080
sigma^2 estimated as 54853104: log likelihood = -557.87, aic = 1119.75
参数检验:参数$\phi _1$的估计值大于它的两倍标准差,参数显著

图 6 无漂移项模型显著性检验图
可看出各阶延迟下白噪声检验统计量的P值都显著大于0.05,可认为拟合模型的残差序列属于白噪声序列,该拟合模型显著成立。
5.4. ARIMA(0,1,1)带漂移项
library(forecast)
fit4<-Arima(x,order=c(0,1,1),method = "ML")
fit4
tsdiag(fit4)Series: x
ARIMA(0,1,1) with drift
Coefficients:
ma1 drift
0.3578 4146.285
s.e. 0.1233 1247.830
sigma^2 = 47791983: log likelihood = -553.1
AIC=1112.19 AICc=1112.67 BIC=1118.16
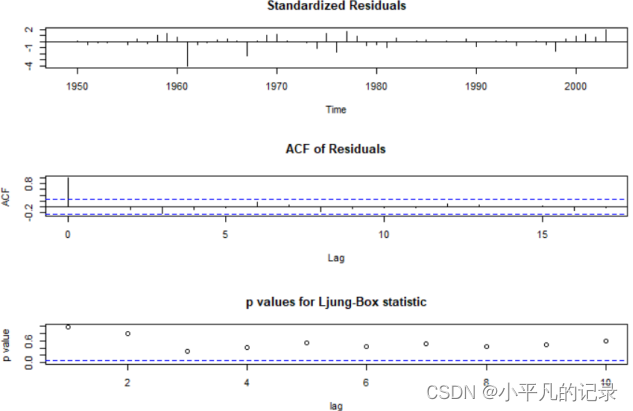
图 7 有漂移项模型显著性检验图
可看出各阶延迟下白噪声检验统计量的P值都显著大于0.05,可认为拟合模型的残差序列属于白噪声序列,该拟合模型显著成立。
参数检验:参数$\phi _1$的估计值大于它的两倍标准差,参数显著;参数的估计值大于它的两倍标准差,参数显著。
6.拟合预测
#预测ARIMA(1,1,0)
library(forecast)
#无漂移项
fore1 <- forecast::forecast(fit1,h=5)
fore1
v <- window(y,start = 2004)
error1<-v-fore1$mean
file1<-data.frame(fore1$mean,v,error1)
file1
plot(fore1)
lines(fore1$fitted,col=2,lty=2)
#有漂移项
fore2 <- forecast::forecast(fit2,h=5)
fore2
v <- window(y,start = 2004)
error2<-v-fore2$mean
file2<-data.frame(fore2$mean,v,error2)
file2
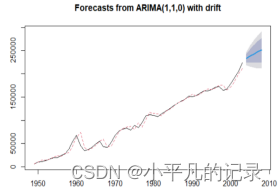
plot(fore2)
lines(fore2$fitted,col=2,lty=2)
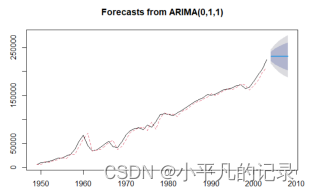
#预测ARIMA(0,1,1)
library(forecast)
#无漂移项
fore3 <- forecast::forecast(fit3,h=5)
fore3
v <- window(y,start = 2004)
error3 <- v-fore3$mean
file3<-data.frame(fore3$mean,v,error3)
file3
plot(fore3)
lines(fore3$fitted,col=2,lty=2)
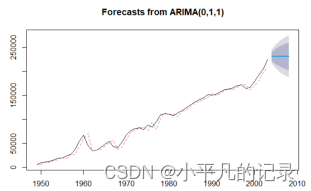
#有漂移项
fore4 <- forecast::forecast(fit4,h=5)
fore4
v <- window(y,start = 2004)
error4<-v-fore4$mean
file4<-data.frame(fore4$mean,v,error4)
file4
plot(fore4)
lines(fore4$fitted,col=2,lty=2)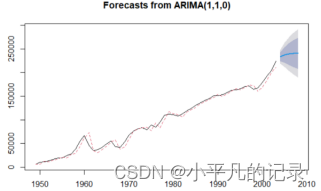
|
fore1.mean |
Volume |
error1 |
fore2.mean |
error2 |
fore3.mean |
Error3 |
fore4.mean |
error4 |
|
|
2003 |
233205.5 |
249017 |
15811.47 |
232773.2 |
16243.77 |
231360 |
17656.96 |
233221.1 |
15795.89 |
|
2004 |
237364.6 |
269296 |
31931.37 |
238194.7 |
31101.26 |
231360 |
37935.96 |
237367.4 |
31928.60 |
|
2005 |
239295.8 |
288224 |
48928.25 |
242721.5 |
45502.45 |
231360 |
56863.96 |
241513.7 |
46710.32 |
|
2006 |
240192.4 |
314237 |
74044.60 |
246990.4 |
67246.56 |
231360 |
82876.96 |
245660.0 |
68577.03 |
|
2007 |
240608.7 |
330354 |
89745.27 |
251185.0 |
79169.02 |
231360 |
98993.96 |
249806.3 |
80547.74 |
由预测值与真实值对比可得,带有漂移项的ARIMA(1,1,0)的预测效果较好,故采用此模型进行预测2009-2013年的数据。
预测结果如下:
|
|
Point Forecast
|
Lo 80
|
Hi 80
|
Lo 95
|
Hi95
|
|
2009
|
341363.1
|
331914.7
|
350811.6
|
326913.0
|
355813.3
|
|
2010
|
349760.7
|
332638.6
|
366882.9
|
323574.6
|
375946.8
|
|
2011
|
356823.1
|
332871.1
|
380775.1
|
320191.7
|
393454.5
|
|
2012
|
363202.9
|
333234.2
|
393171.5
|
317369.7
|
409036.0
|
|
2013
|
369233.6
|
333931.8
|
404535.4
|
315244.1
|
423223.1
|
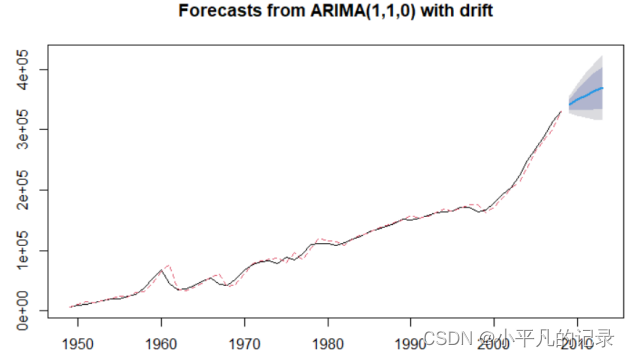
图 12 预测2009-2013年的铁路货运量


 浙公网安备 33010602011771号
浙公网安备 33010602011771号