动手学深度学习 | 自注意力 | 67
自注意力

在介绍transformer之前,先讲一个比价重要的东西=》 self-attention。self-attention其实没有什么特殊的地方,主要就是key,value,query到底要怎么选择,自注意力机制有自己的一套选法。


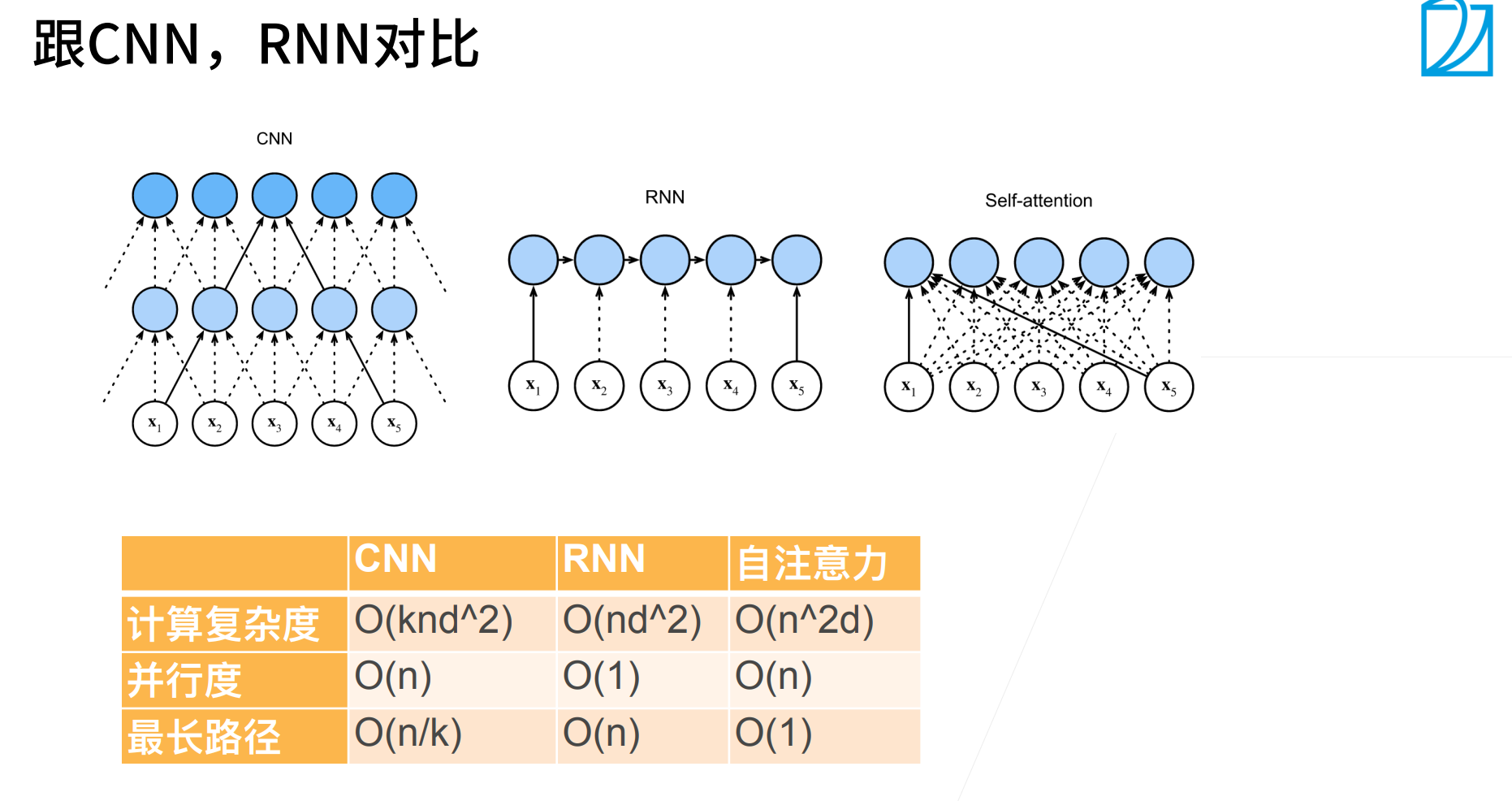
CNN,RNN,self-attention都可以用来处理序列。
CNN要实现序列处理,其实就相当于每次处理当前时刻都会看一个window,当然只是非常局限的。
计算复杂度 & 并行度 & 最长路径

self-attention的计算量是非常大的,一般训练一个都是要几千个GPU。






讲完了CNN,我们要讲另外一个常见的network架构,这个架构叫做self-attention。
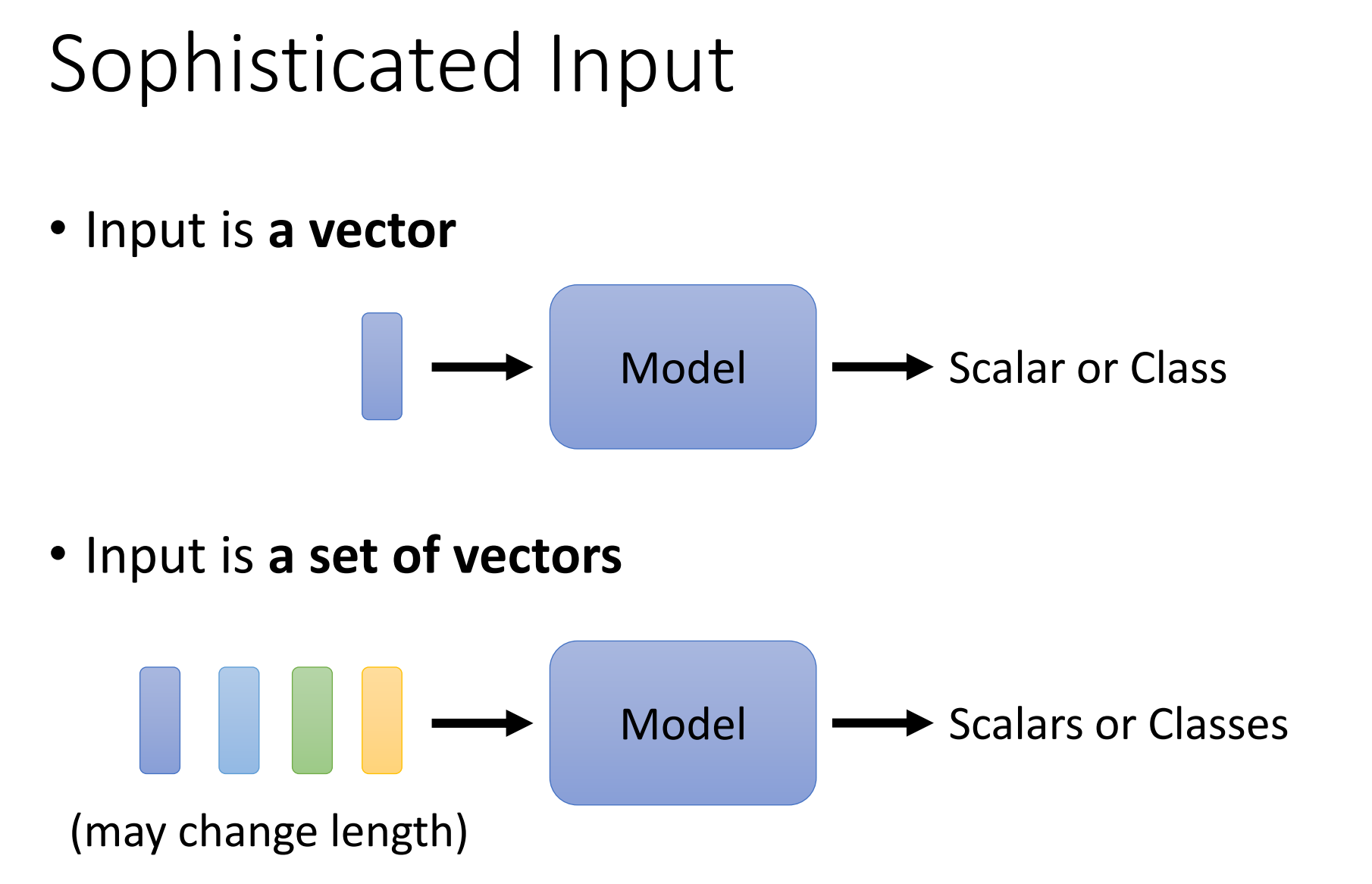
而这个self-attention想要解决的问题是什么呢?
到目前为止,我们为network的input都是一个向量,然后输出可能是一个数值(回归),也可以是一个向量(分类)。但假设我们遇到更复杂的问题呢?假设我们说输入是一排向量,而且这个输入的向量数目是会改变的,也就是每次输出的sequence的长度都会不一样(变长的序列问题)

一个变长序列的例子就是文字处理,比如“this is a cat”,四个token可以用四个向量来表示,当然只是这个句子有四个token,如果是更长的句子,那么向量的数目会更多,也就是vector set的大小会不一样。
那么如何把一个词汇表示成一个向量呢?最简答的做法就是one-hot的encoding。但是使用one-hot有一个非常严重的问题=> 就是one-hot假设所有token之间都是没有关系的(离散的)。如上图,不能看到说cat和dog比较接近,都是动物;也看不出apple和cat其实一个是植物,一个是动物,并没有什么关系。也就是one-hot编码中没有任何的语义信息。
有另外一个方法就是 word embedding。我们会给每一个词汇一个向量,而这个向量是有语义的信息的。如果你把word embedding画出来,你会发现所有的动物会聚集在一块,所有的植物会聚集在一块,所有的动词可能聚集在一块。word embedding如何得到的?这不是这次课的重点,如果想要知道可以看有关的录影https://www.youtube.com/watch?v=X7PH3NuYW0Q。现在在就可以在网络上下载到word embedding,然后会给一个词汇一个向量,而一个句子就是一排长度不一的向量。
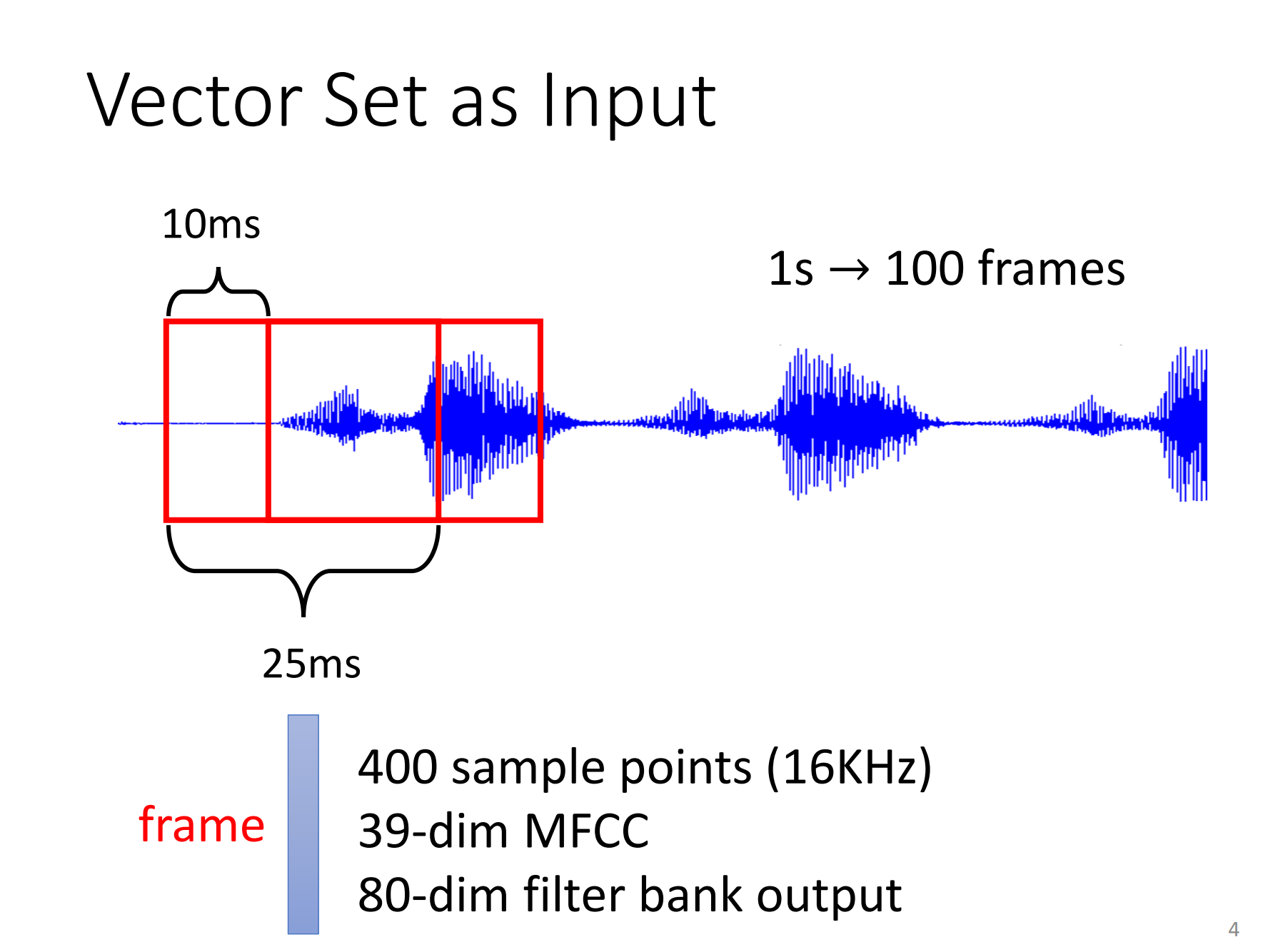
一段声音也是一排向量的输入。我们会把一段声音讯号取一个范围,叫做一个window,把这个window里面的资讯描述成一个向量,这个向量叫做一个Frame,在语音上我们会把一个向量叫做一个Frame。通常这个window的长度就是25个ms。如何把一个Frame的声音变成一个向量呢?上面列出了3种做法。
通常移动Frame的大小为10ms,那为什么是10ms?这个问题很难回答,这是古圣先贤给你调好的,你自己调放结果可能会差,他们都已经可能的情况都试过了。 总之呢,一段声音讯号就是一串向量来表示。1s的声音有100个向量(100个Frame)

还有什么东西是一堆向量呢?一个graph,一个图也是一堆向量。
social network上面的每一个节点就是一个人,节点和节点之间的边是他们的关系。而每一个节点可以看做是一个向量。也就是一个graph可以看做是一堆向量组成的(一个节点就是一个向量)。
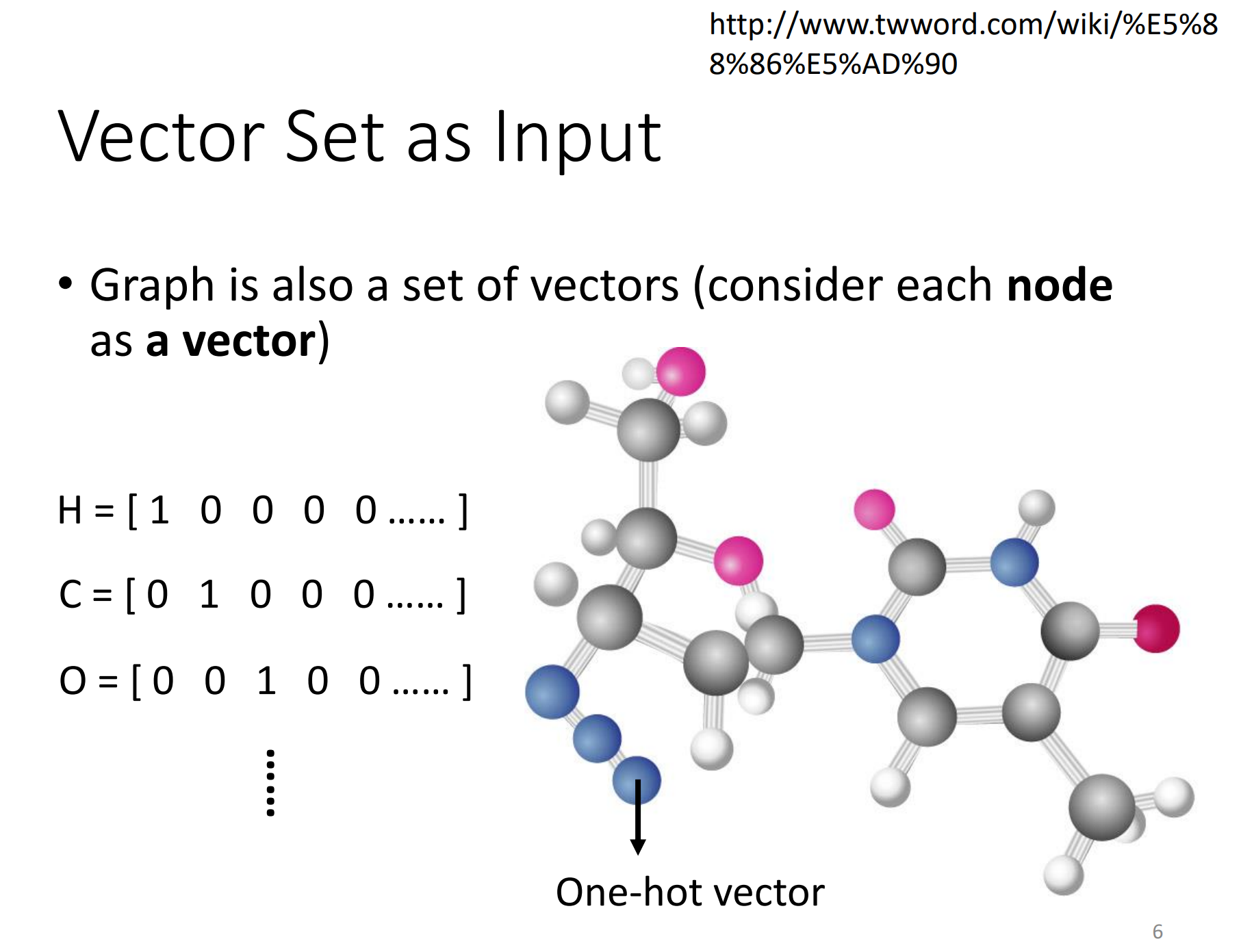
分子也可以看做是一个graph。现在像这种但drug discovery的应用,非常地受到重视。可以把一个分子(graph,一堆向量)当做是你的模型的输入。分子上面的每一个节点,可以看做是一个向量,这里可以使用one-hot编码表示。
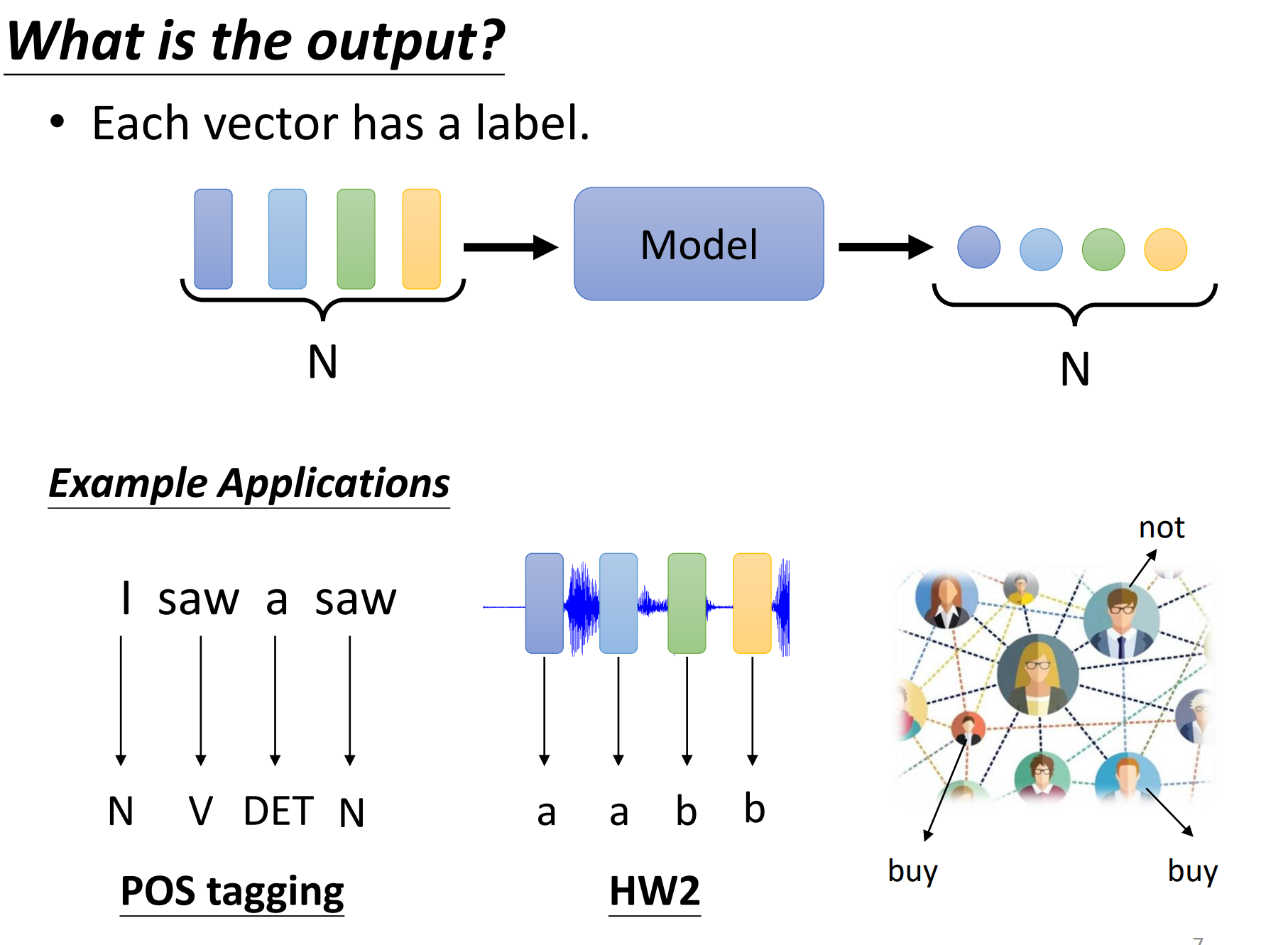
那输出是什么?我们刚刚看到了说输入的一堆向量,可以是文字、语音、graph。那这时候,我们有可能有什么样的输出呢?有三种可能性。
第一种可能性:每一个向量都有一个对应的label。也就说当你的模型,看到输入是四个向量的时候,它就要输出4个label,而每一个label它可能是一个数值,那就是regression问题;如果每个label是一个class,那就是一个classification的问题。
但是在第一种可能性里面,输入和输出的长度是一样的,所以模型不需要去烦恼,要输出多少的label,输出多少的scale,反正输入是4个向量,输出就是4个label。
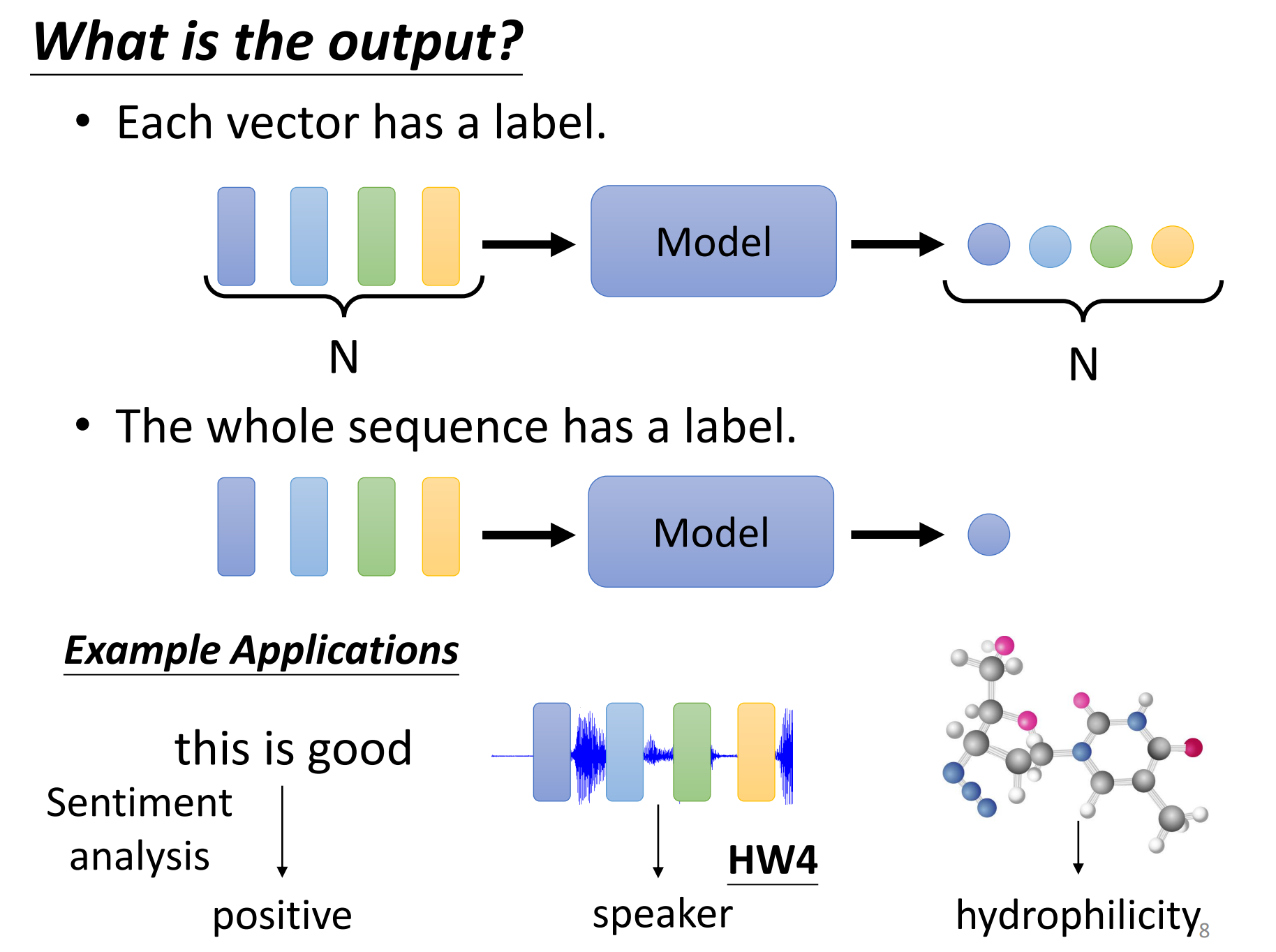
还有就是一堆向量输入,但是只有一个输出的label。
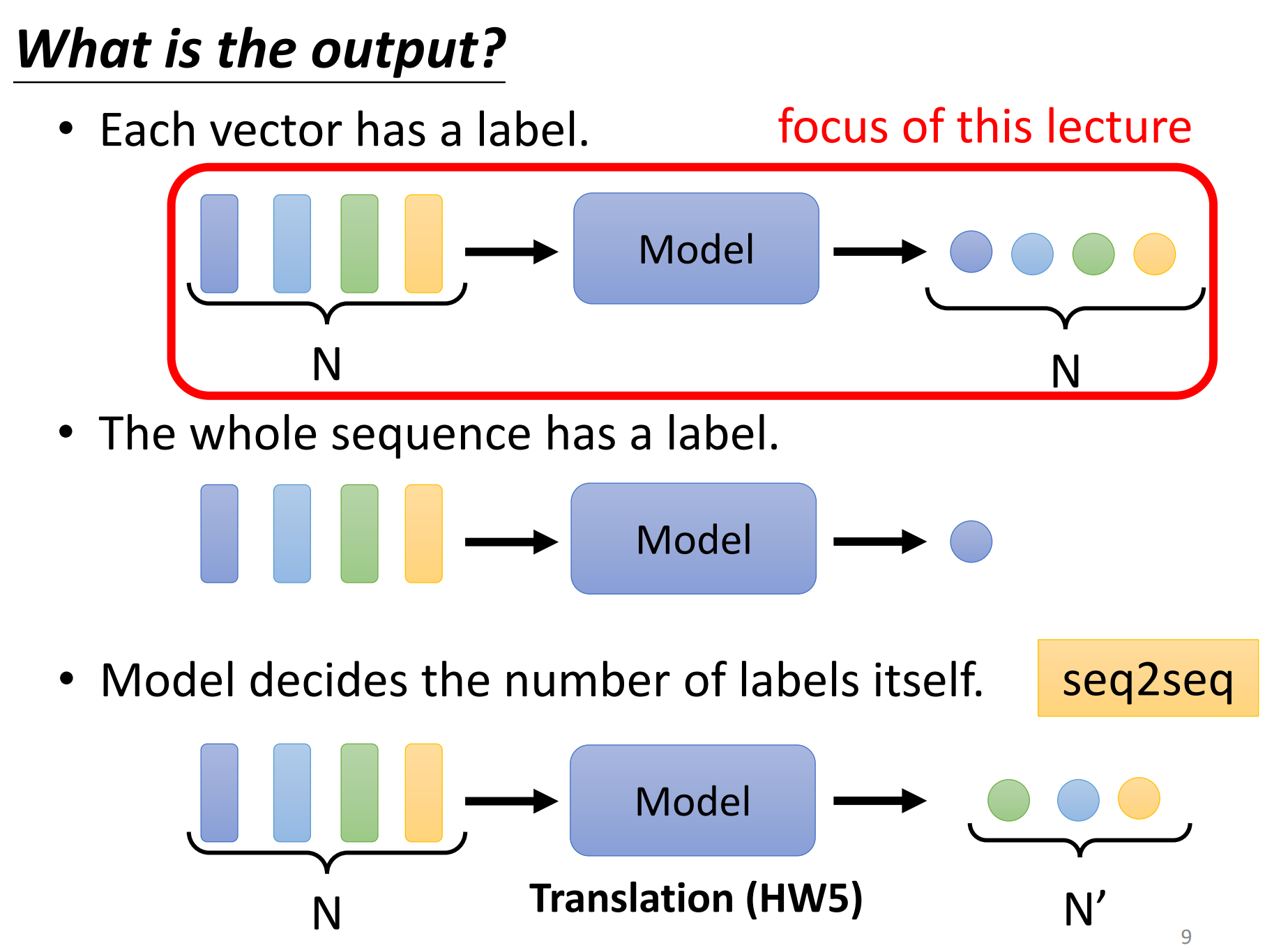
还有一种是一堆向量输入,也有一堆label输出,这个也是seq2seq的问题。
今天我们只讲第一种类型,也就是输入和输出数目一样多的情况。
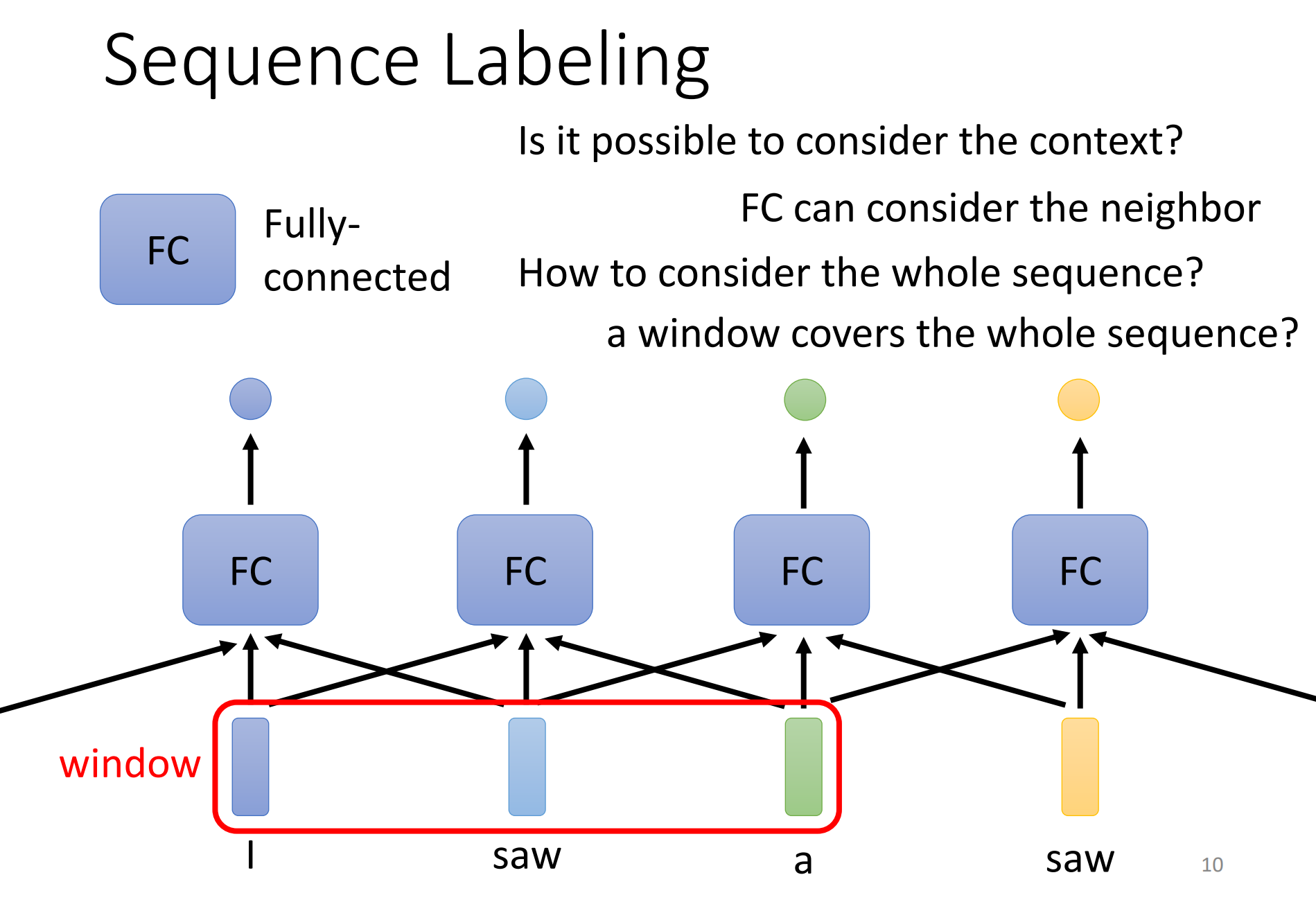
这种输入和输出一样多的情况也叫做 sequence labeling。需要给sequence里面的每一个向量都给它一个label。
那怎么解决sequence labeling的问题呢?一个非常简单的做法就是不要管他是一个sequence,就把sequence里面的一个一个向量都单独拿出来,分别输入一个FC中,分别得到一个label。但是这样做一个非常大的缺点,比如是词性标记问题,输入“I saw a saw”,那么2和4的不能正确区别的,因为没有前后的语义信息。对于FC来说,第一个saw和第二个saw就是一样的东西,没有理由输出不同的东西,但是实际上,你期望第一个saw输出动词,第二个saw输出名词。那如何让FC能够考虑上下文的资讯呢?其实也很简单,就是直接把前后几个向量都丢到一个FC中就好了,我们可以结合这个FC层的前面5个和后面5个FC,也就是总共结合了11个FC才决定了最后的输出。也就是我们可以给FC一整个windows的资讯,让它可以考虑上下文。
但是这样的方法是有极限的,比如说如果是边长的序列呢?那么这个Window要多大?其实是很难确定的。就算window可以把每一个sequence都盖住,那么也就意味着FC它需要非常多的参数,除了运算量很大,也会非常容易的overfitting。

所以有没有更好的办法来考虑整个input sequence的资讯呢?那么就需要用到self-attention这个技术。self-attention如何运作呢?self-attention会吃一整个sequence的资讯,然后你input几个vector,它就输出几个vector,而且这些输出的vector都是考虑了整个sequence以后才得到的,那么self-attention如何考虑一整个sequence的资讯,这个后面会讲。
上图output的向量,我们都给了一个黑色的框框,代表其不是一个普通的向量,而是一个考虑了整个sequence后才得到的向量。然后再讲考虑了整个sequence资讯的vector丢进FC,再来说决定它应该是什么东西。如此一来,FC考虑的就不是一个window的语义,而是整个结合了整个sequence资讯的向量。
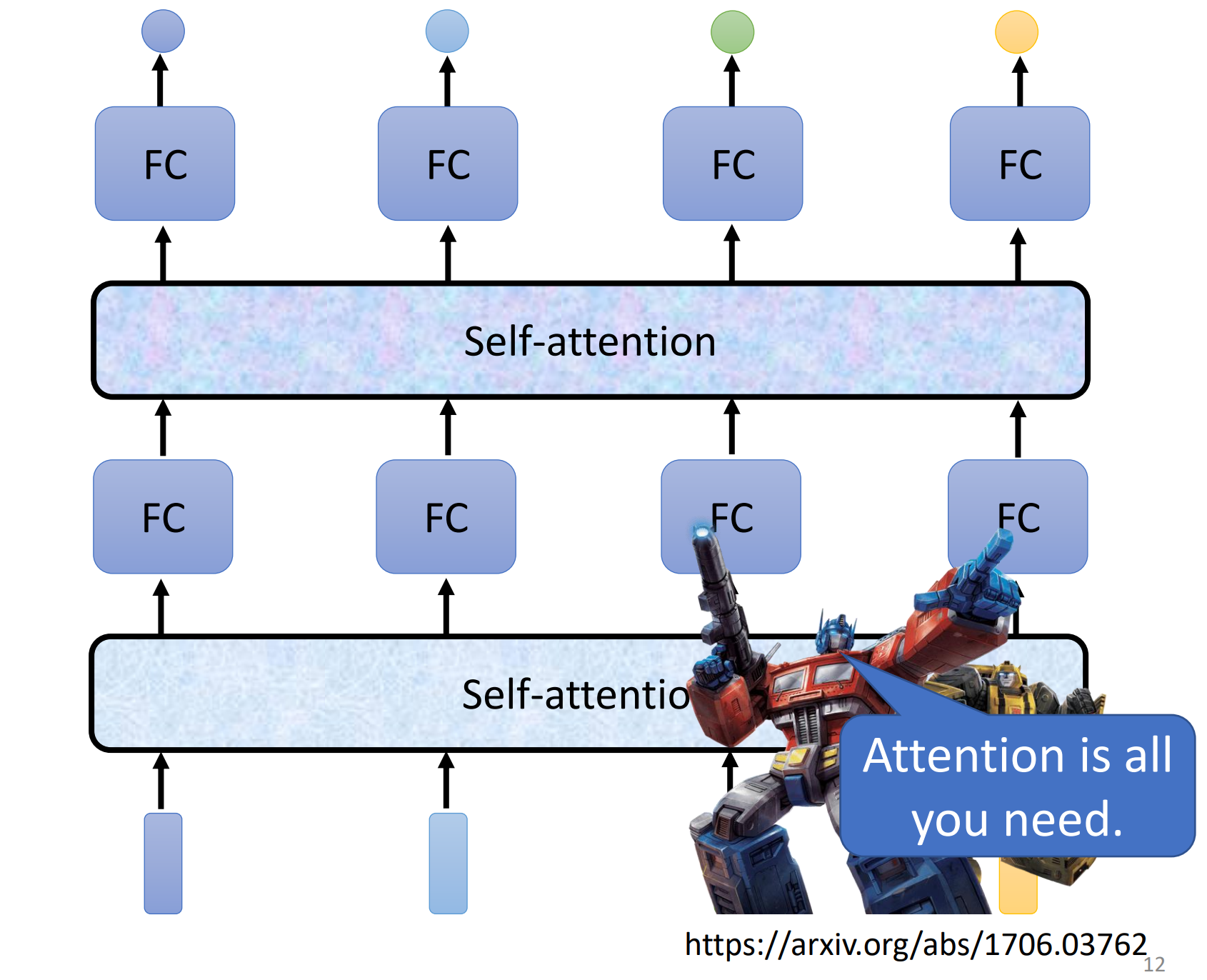
而且self-attention不止可以使用一次,可以叠加很多次,也就是可以再重新考虑一次下一层input的sequence的资讯信息。所以是可以把self-attention和FC进行交替使用的=》 self--attention处理整个sequence的资讯,而FC专注于处理某一个位置的资讯,然后可以再用self-attention再把整个sequence再处理一次。
有关于self-attention最知名的文章,就是attention is all your need,也就是在这个paper提出了transformer这样的network架构。那么在transformer里面一个最重要的module就是self-attention。
像self-attention这样的结构不是说出现在attention is all your need这篇paper中,因为其实很多更早的paper就提出了类似的架构,只不过不见得叫做self-attention,类似叫做self-matching,不过是attention is your need 讲self-attention 这个module发扬光大。

那么self-attention是怎么运作的呢?self-attention的input就是一串vector,这个vector可能是你整个network的input,它也可能是某个hidden layer的output,所以这里不是使用x来表示,而是使用a来表示,代表说它有可能是前面已经经过了一些处理了,它是某个hidden layer的output。那么input一排a的向量以后,self-attention要output另外一排b这个向量,那么这个output的b呢,每一个都是考虑了所有的a以后才生成出来的,所以这边画出了许多的箭头,告诉你说\(b^1\)考虑了\(a^1\)到\(a^4\)而产生,\(b^2\)考虑了\(a^1\)到\(a^4\)而产生,\(b^3,b^4\)也是一样的,考虑整个input的sequence才产生出来的。
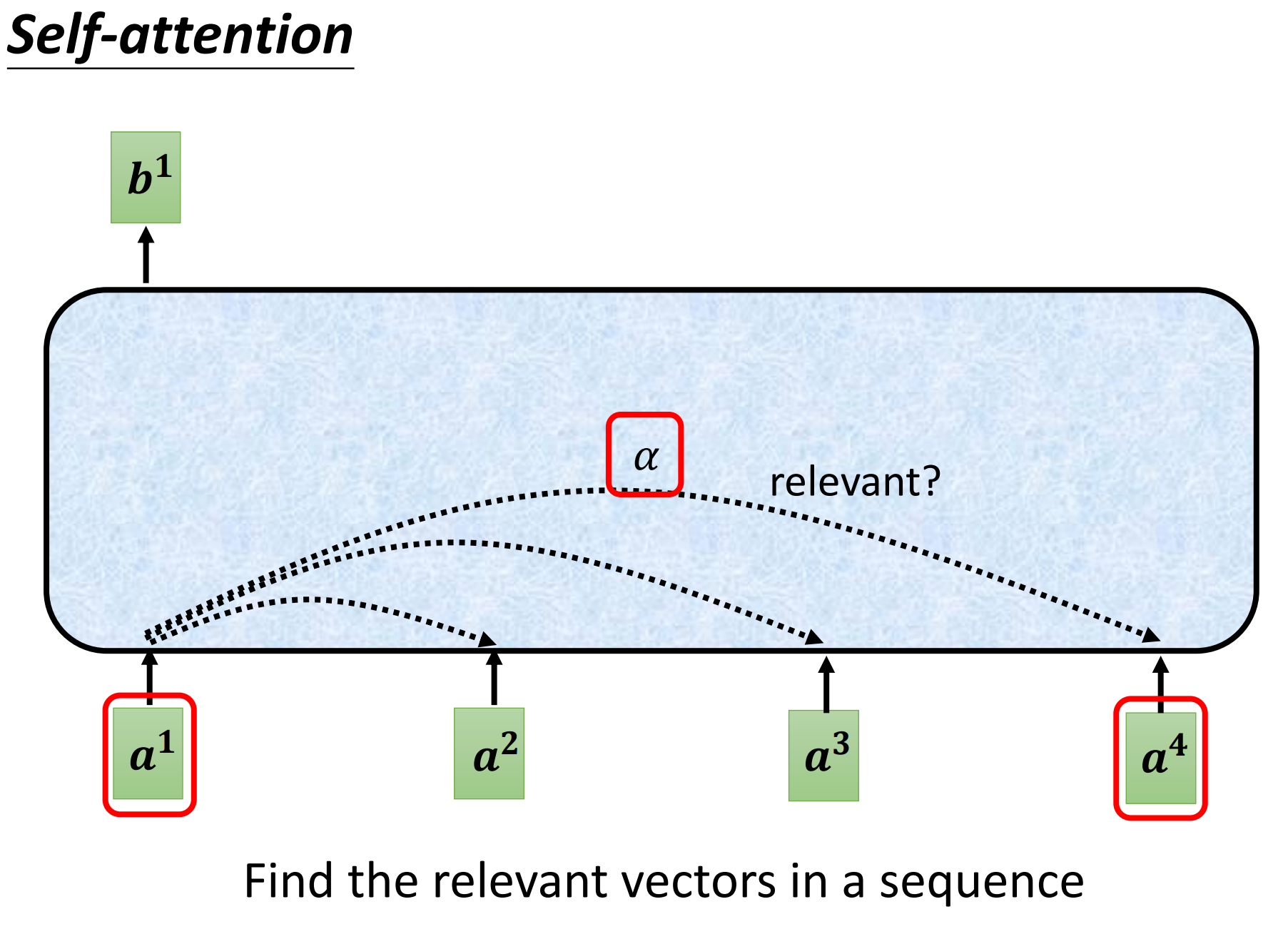
那么接下来就是要说明如何产生\(b^1\)这个向量,那你知道如何产生\(b^1\)之后,那么\(b^2,b^3,b^4\)也都是同理。第一个步骤,根据\(a^1\)找出这个sequence里面跟\(a^1\)相关的其他向量,我们知道说我们今天要做self-attention的目的就是为了考虑整个sequence,但是我们又不希望把整个sequence的资讯都包含在一个window中,所以我们有一个特别的机制,这个机制是根据\(a^1\)这个向量,找出整个很长的sequence里面到底那些部分是重要的,哪些部分跟判断\(a^1\)是哪一个label是有关系的,哪些部分是我们要决定\(a^1\)的class,决定\(a^1\)的regression数值的时候,所需要用到的资讯。
那每一个向量跟\(a^1\)的关联程度,我们用一个数值叫\(\alpha\)来表示,再来的问题就是这个self-attention的module怎么自动决定两个向量之间的关联性呢?给定两个向量\(a^1,a^4\),它怎么决定\(a^1,a^4\)有多相关,然后给定一个数值\(\alpha\)呢?
这里需要一个计算attention的模组,这个计算attention的模组呢,它就是拿两个向量作为输入,然后它就直接输出\(\alpha\)这个数值,那你就可以把\(\alpha\)这个数值当做两个向量的关联程度。
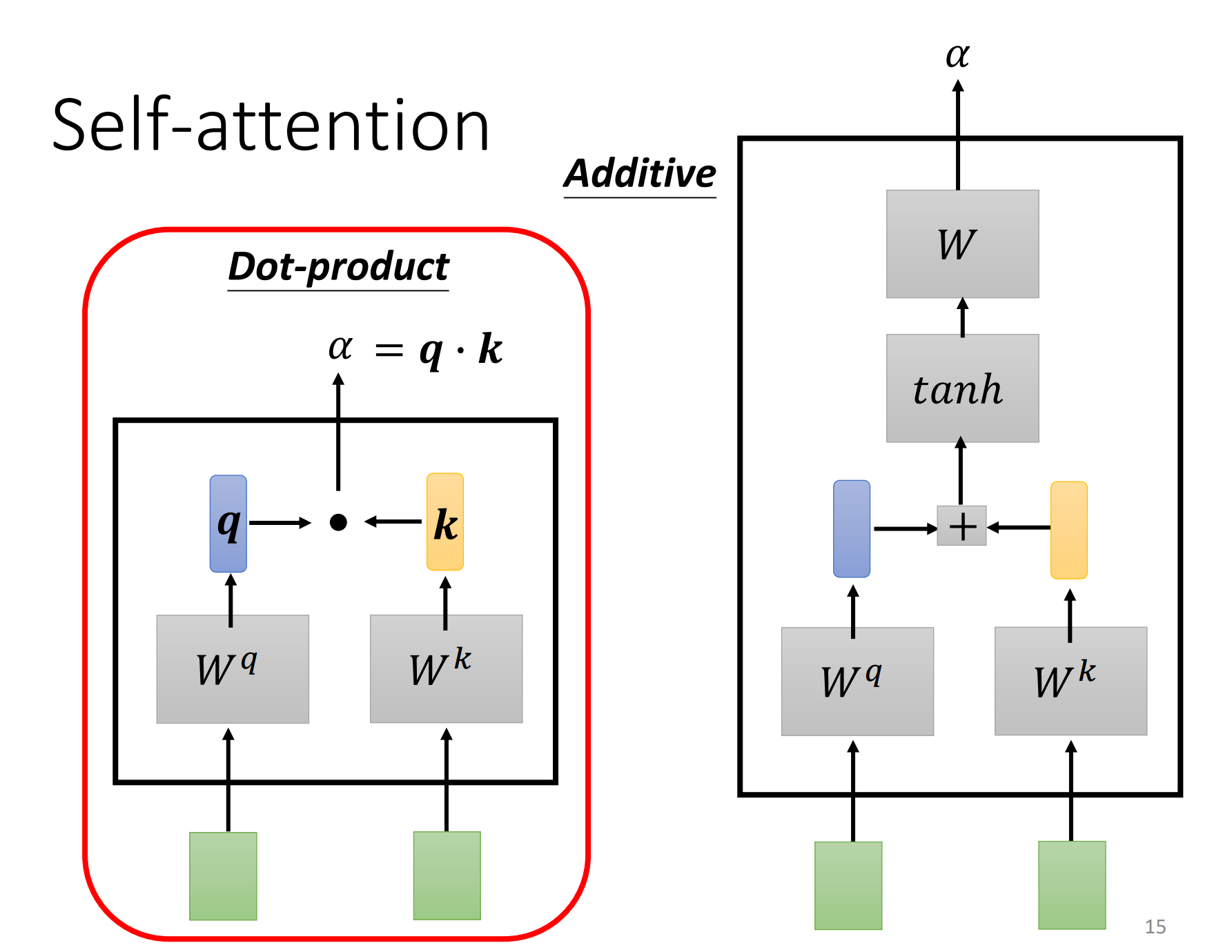
那怎么计算\(\alpha\)的数值呢?这边就有各种不同的做法,比较常见的做法有两种:dot-product & additive。
- dot-product
把输入的向量,分别乘上两个不同的矩阵,比如输入矩阵\(W^q,W^k\),然后输出向量\(q,k\),再将这两个向量进行element wise相乘,再全部加起来以后就得到了一个scalar(标量)$ \alpha =q\cdot k$。
- additive
同样是输入矩阵\(W^q,W^k\),然后输出向量\(q,k\),然后将\(q,k\)串起来,经过一个tanh,在经过一个矩阵得到\(\alpha\)。
总之有非常多的方法可以计算attention,可以计算\(\alpha\)这个数值,可以计算这个关联程度,但是在接下来的讨论里面,我们都只用dot-product这个方法,这也是今日最常用的方法,也是用在transformer里面的方法。
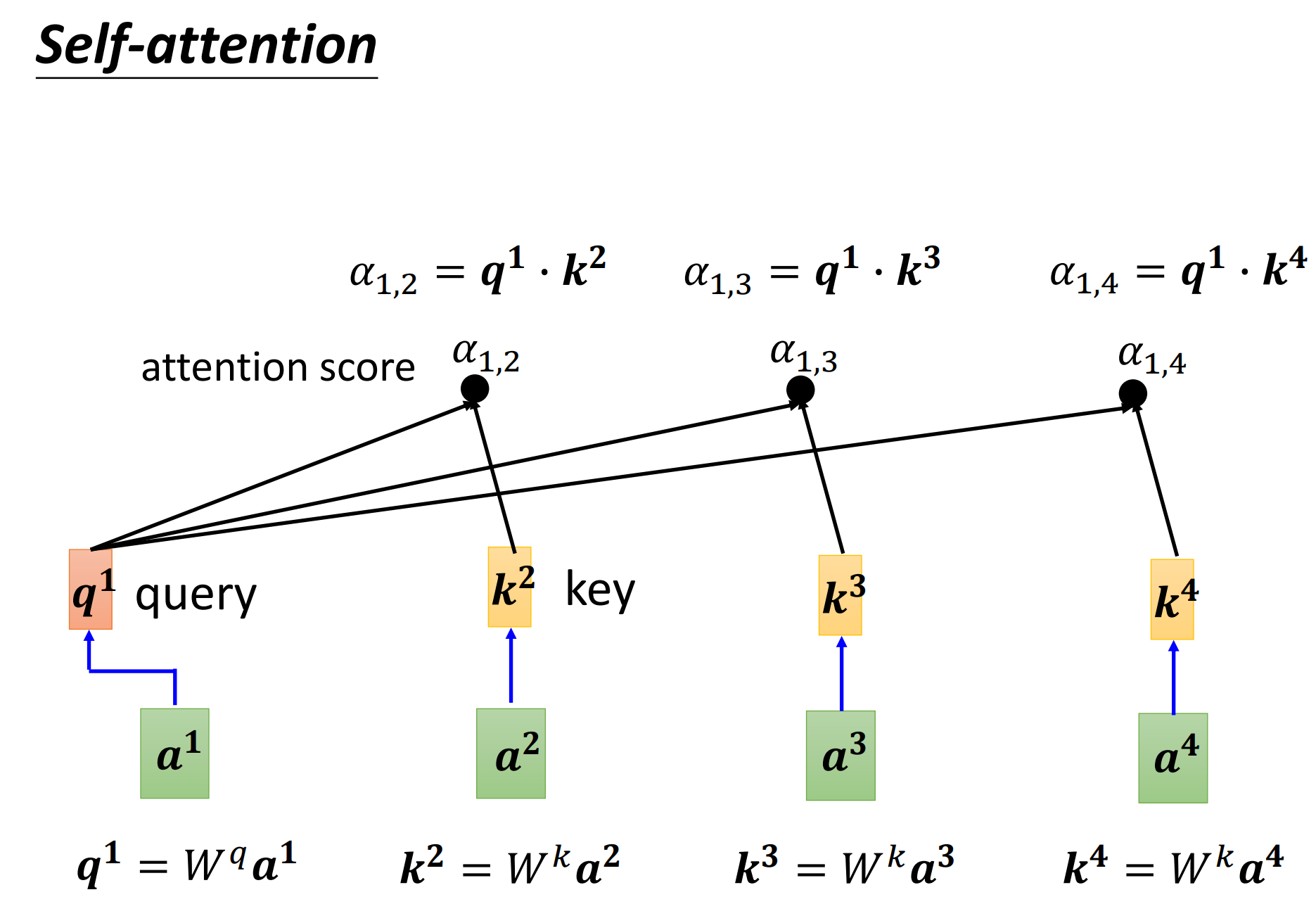
前面已经讲解了如何计算attention的关联性\(\alpha\),那么这里怎么将其套用在self-attention中呢?那你就要把\(a^1\)去跟\(a^2,a^3,a^4\)分别去计算他们之间的相关性\(\alpha\)。
把\(a^1\)乘上\(W_q\)得到\(q_1\),那这个\(q\)有一个名字,我们叫做query。
然后\(a^2,a^3,a^4\)都要去乘上\(W^k\),得到\(k\)这个vector,这里我们把k叫做key。
那么这里把query \(q^1\) key \(k^2\)算inner-product就得到\(\alpha\),我们这边用\(\alpha_{1,2}=q^1\cdot k^2\)代表说query是1提供的,key是2提供的时候,这个1和2的关联性,也叫做attention score。那么同理,和其他元素同样计算得到\(\alpha_{1,3},\alpha_{1,4}\),当然自己和自己也是要计算一个相关性/注意力分数的 \(\alpha_{1,1}\)。
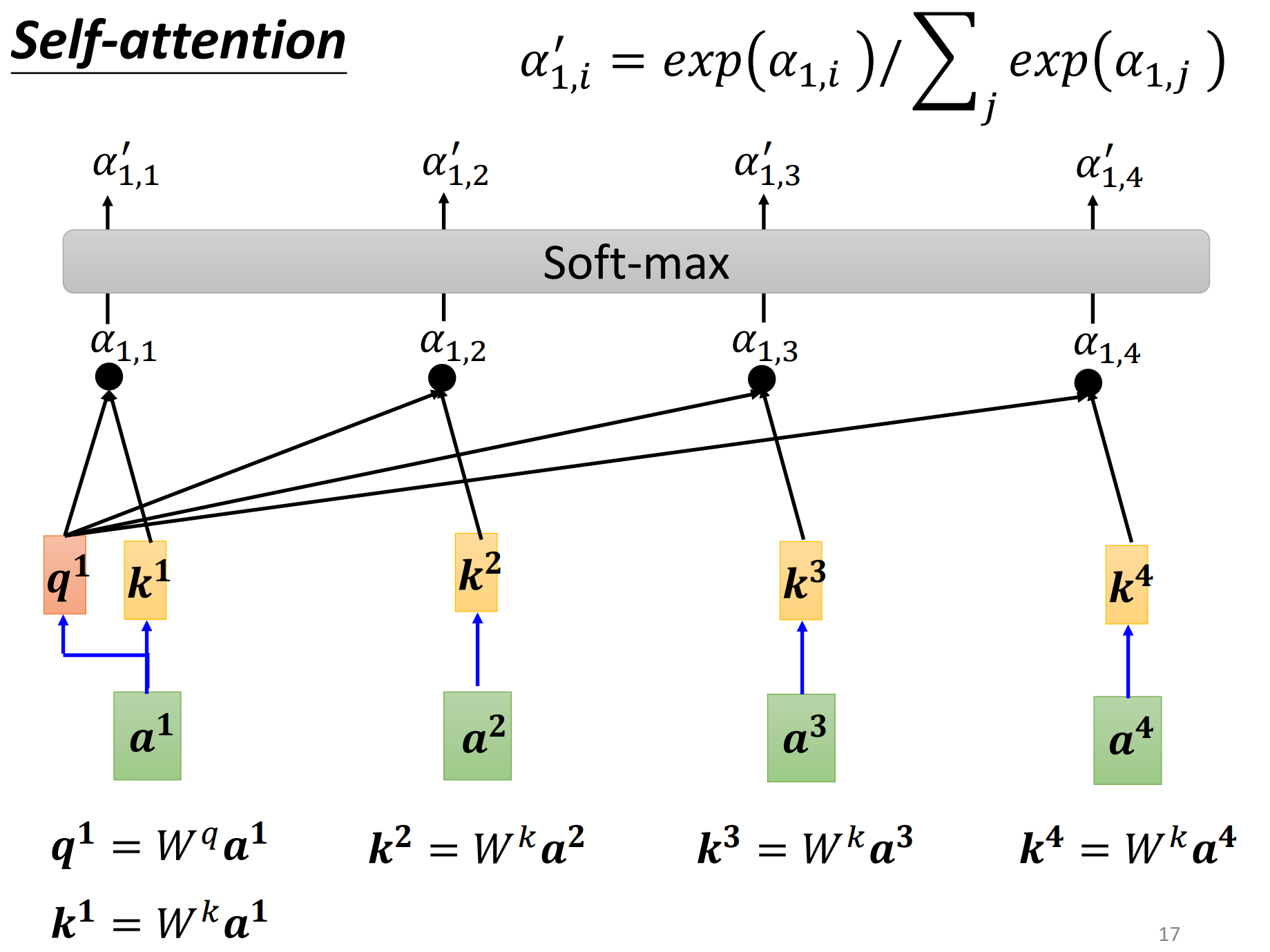
这里也是要有\(k^1\)的,也要计算出\(a^1\),自己和自己计算关联性这个事情还是比较重要的,可以实验的时候试试看。
那我们计算出\(a^1\)和每个向量的关联性(包括自己),那么接下来会作为一个softmax,把\(\alpha\)全部乘上一个exp,在把全部exp的值加起来做做一个normalize得到\(\alpha'\),softmax的输出就是一排\(\alpha'\)。
这里不一定要用softmax,有人尝试过使用RuLU结果发现结果还比使用softmax好一些,只不过softmax是最常见的。\(\alpha '_{1,i}=\exp (\alpha _{1,i})/ {\textstyle \sum_{j}^{}} \exp(\alpha _{1,j})\)

得到这个\(\alpha'\)以后,接下来我们就要根据这个\(\alpha'\)去抽取这个sequence里面重要的资讯,根据这个\(\alpha'\)我们已经知道说哪些向量跟\(a^1\)是最有关系的,接下来我们根据这个关联性(attention socre)来抽取重要的资讯。怎么抽取重要的资讯呢?我们会把\(a^1\)到\(a^4\)这边的每一个向量乘上\(W^v\)得到新的向量,分别使用\(v^1,v^2,v^3,v^4\)来表示,接下来把\(v^1\)到\(v^4\)每一个向量都去乘上这个attention分数,然后再加起来,得到\(b^1\),如果某一个向量它得到的分数越高,比如说\(a^1\)跟\(a^2\)的关联性很强,这个\(\alpha'_{1,2}\)得到的值很大,那么最后的得到\(b^1\)的值就可以会比较接近\(v^2\),也就是谁的\(v\)的值越大,就会dominant抽出来的结果。

那刚刚就说完了如何从一个整个sequence得到\(b^1\)。

计\(b^1\)到\(b^4\)并不需要依次计算,没有前后关系,他们是同时被计算出来的。
这里计算如何得到\(b^2\),来巩固一下self-attention的计算过程。
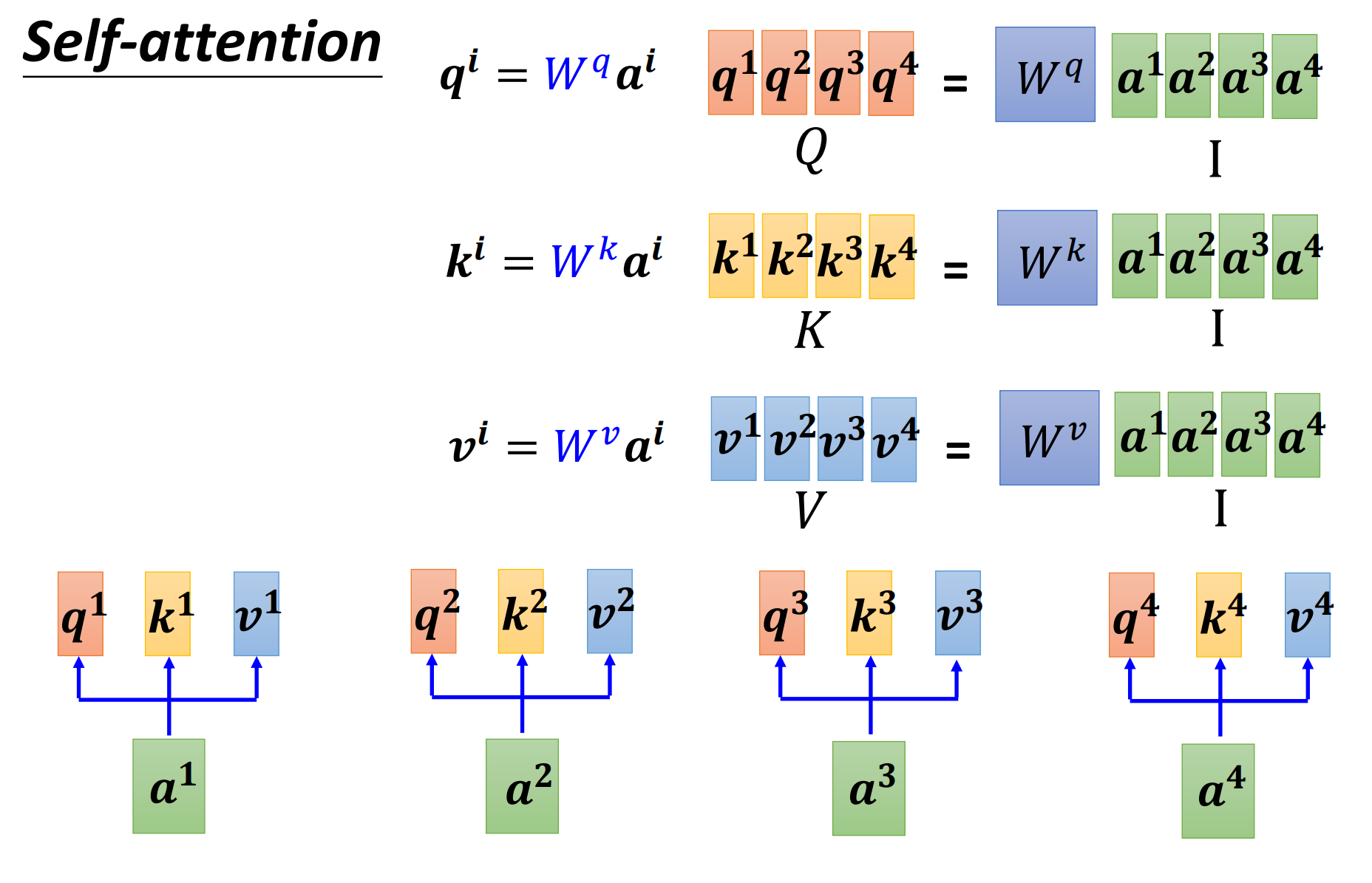
接下来我们从矩阵乘法的角度,再重新讲一次我们刚才讲的self-attention是怎么运作的。
每一个\(a\)都要分别产生\(q,k,v\),如上图,使用\(Q,K,V\)来表示\(q^i,k^i,v^i\)组成的矩阵。

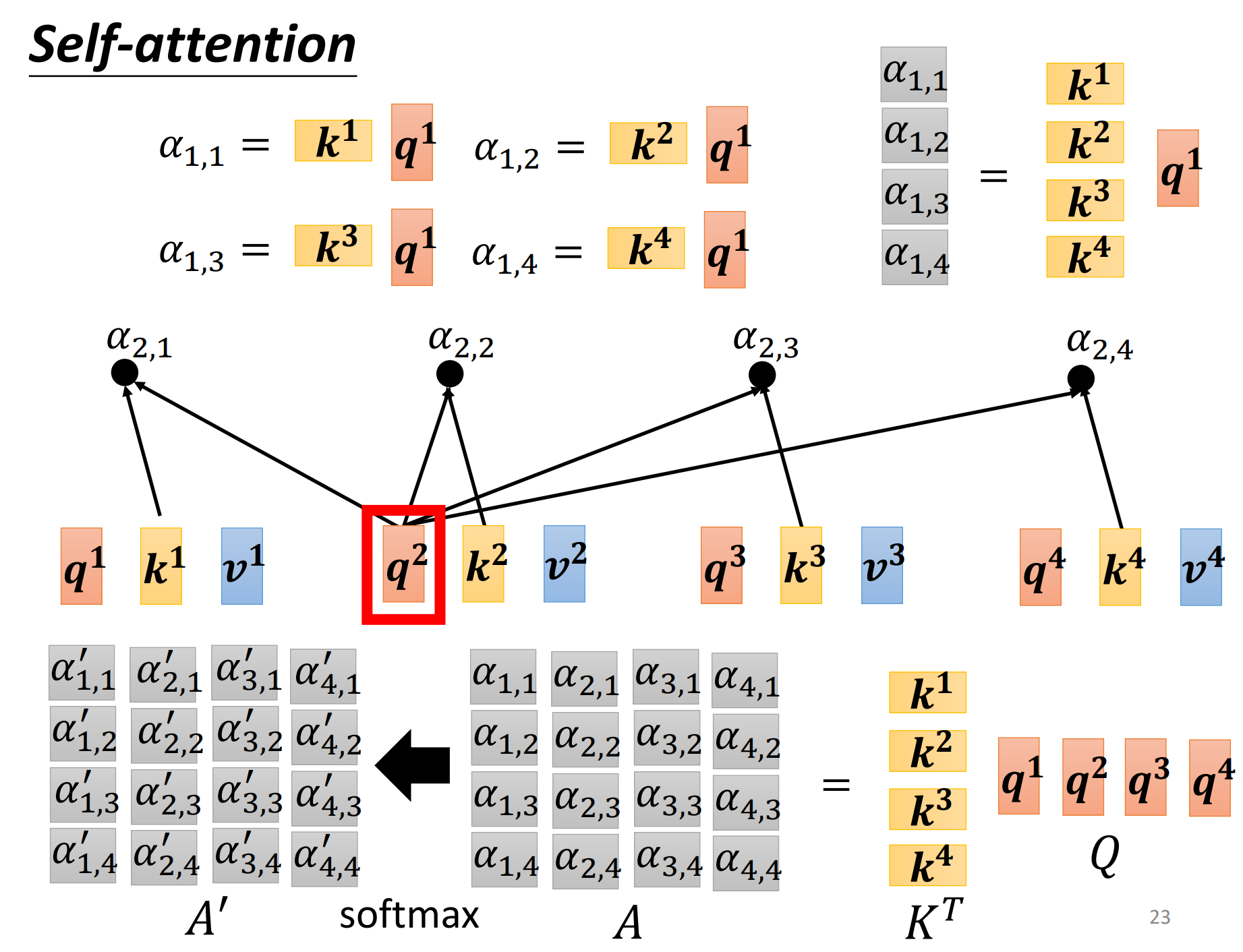
$A = K^T \cdot Q $
\(A' = softmax(A)\)

\(O=VA'\)

self-attention layer中其实就是一系列的矩阵乘法,唯一需要学习的参数就只有\(w^q,w^k,w^v\)而已,也是需用通过参数训练来学习的。
上面从输入\(I\)到输出\(O\)就是一个self-attention的操作。
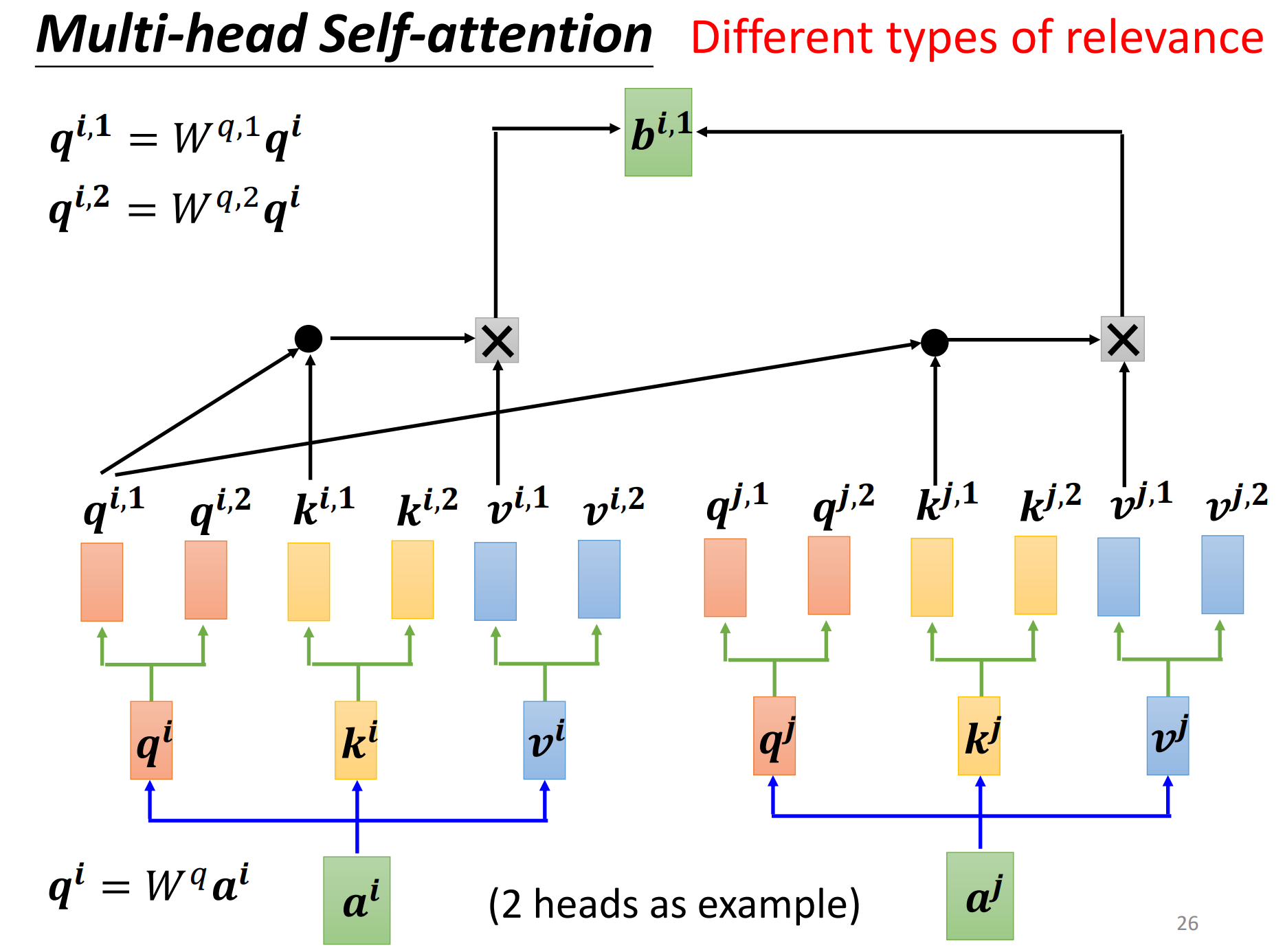
self-attention有一个进阶的版本,那就是multi-head self-attention,而且在今天的使用是非常广泛的。
这个head的数量也是一个超参数,需要自己进行调整。
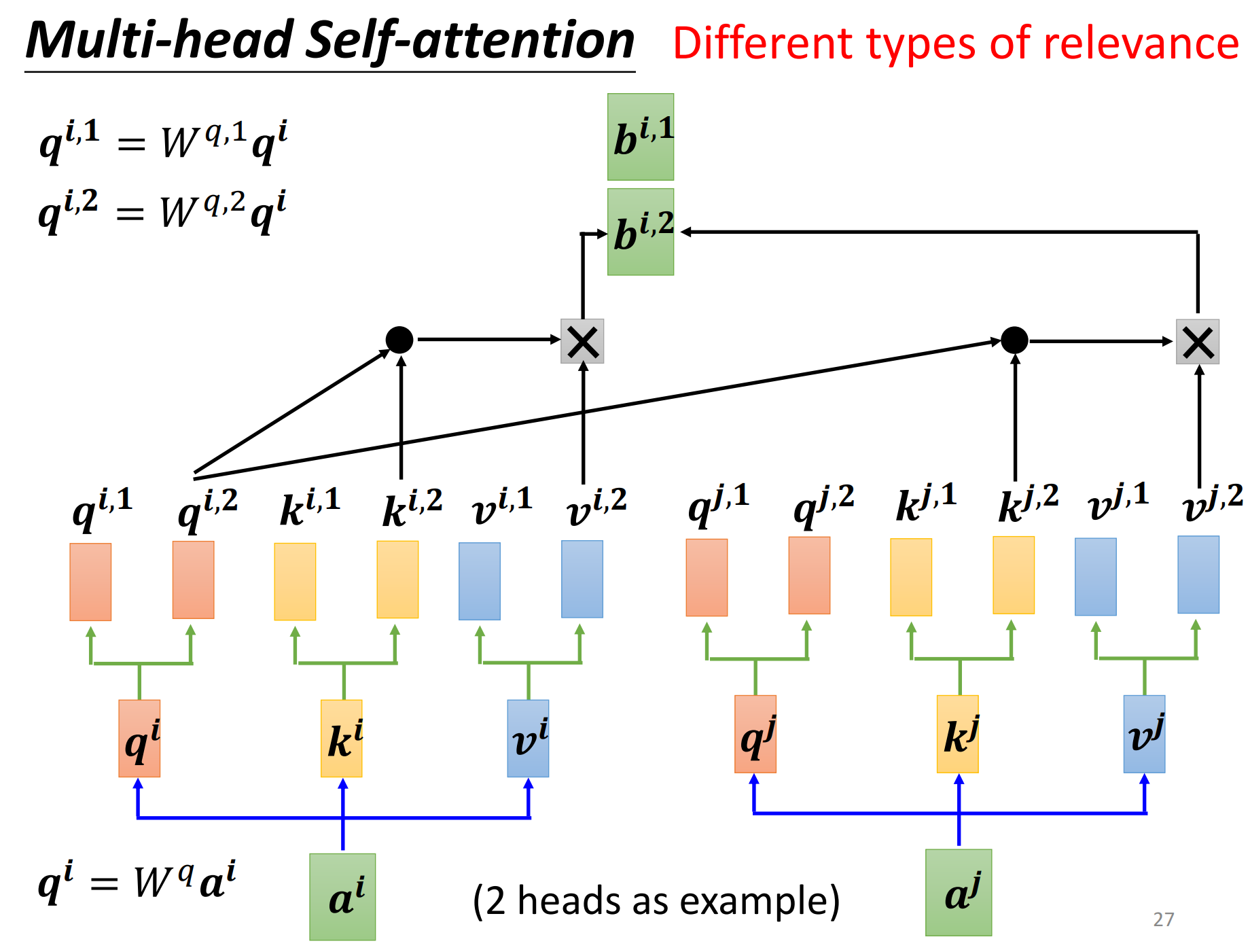
我们使用q去找相关的k,但是相关这件事情有很多不同的形式,有很多种不同的定义,所以也许我们不能只要一个q,我们应该要有多个q,不同的q负责不同类型的相关性。
在q的基础上,再乘两个矩阵(看看具体是几头了)分别得到\(q^{i,1},q^{i,2}\),也就可以认为有两个head,认为里面有两种不同的相关性。那么同理了,q有两个,那么k也要有两个,v也要有两个。都是分别乘上两个矩阵,两个矩阵,两个矩阵。
然后做self-attention,1的那一类一起做,2的那一类一起做。


讲到目前位置,你会发现self-attention这个layer它少了一个很重要的资讯,也即是位置资讯。
对于self-attention而言,每一个input它是出现在sequence的最前面还是最后面,它是完全没有这个资讯的。但是这是个问题,因为有时候位置的资讯也许很重要,比如POS tagging词性标记,也许你知道说动词比较不容易出现在句首,所以我们知道说一个词汇是放在句首的,那它是动词的可能性就会比较低,会不会这样的位置资讯往往也是有用的。
位置资讯要塞进self-attention中,这里需要用到一个叫做position encoding的技术。这个技术是这样子的,为每一个位置设定一个vector,叫做position vector,这边用\(e^i\)表示,上标i代表的是位置,每一个不同的位置就有不同的vector,就是\(e^1\)是一个vector,\(e^2\)是一个vector。然后把这个\(e^i\)加到\(a^i\)上面,就结束了。
上图展示的就是一个人设的position encoding,透过某个规则产生的,一个很神奇的sin,cos的function所产生的,当然不只这种方式可以产生,这还是一个待研究的问题。

上面是各种产生的position encoding的展示,有各种各样产生position encoding的方法,目前还不知哪种方法是最好的。

这个self-attention当然是用的很广的,我们已经提过很多次transformer这个东西,那么大家也知道说NLP领域有一个叫做BERT,BERT里面也用到self-attention,所以self-attention在NLP上面的应用是大家都耳熟能详的。
但是self-attention不是只能用在NLP相关的应用上,它还可以用在很多其他的问题上。
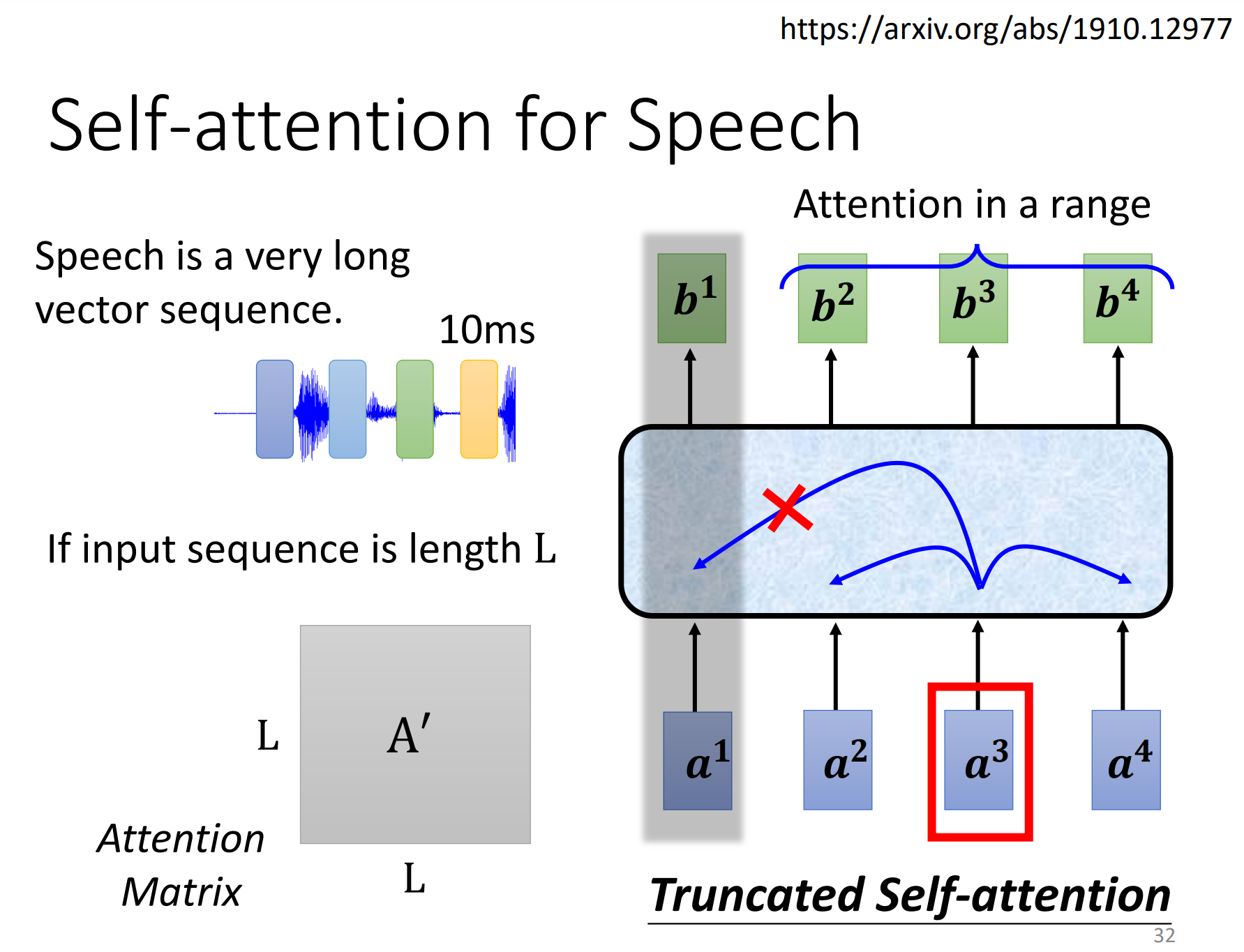
在做语音的时候,也是可以用到self-attention。(不做了解)
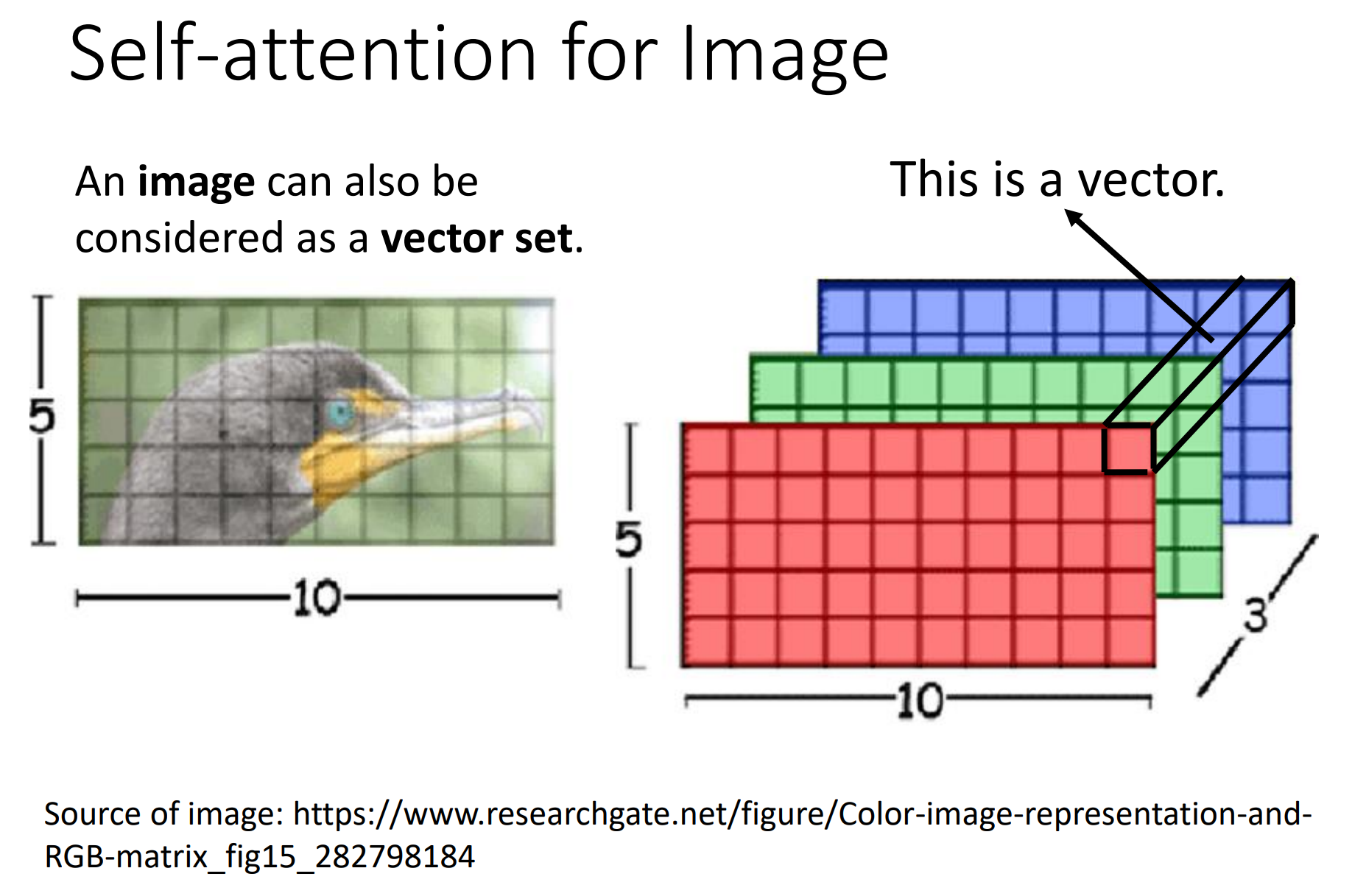
self-attention也可以用在图像上。我们讲self-attention的适用范围是输入一排向量的时候,输入是一个vector set的时候,它适合用self-attention。图片就是一个\((c,w,h)\)的vector set,如果也是一个vector set的话,完全也是可以用self-attention来处理一张图片。

有没有人来用self-attention来处理一张图片呢?有的,这里给了两个例子。

我们可以比较一下self-attention和CNN之间有什么差异或者是关联性?
如果我们今天是用self-attention来处理一张图片,假设是考虑中心pixel,那它产生query,右下角的pixel产生key,那么这里做inner product就不是考虑小的感受野(卷积核范围),而是整张图像的资讯。CNN是有固定的receptive field,也只考虑这个感受野里面的内容。所以我们比较CNN和self-attention的话,我们可以把CNN看做是一种简化版的self-attention,因为CNN只考虑receptive field里面的资讯,而self-attention是考虑整张图片的资讯。或者可以反过来说,self-attention是一个复杂化的CNN,CNN的receptive field是人为规定的大小,那么self-attention去找相关的pixel就好像是receptive field是自动被学出来的,network自己决定说receptive field的形状长什么样子,network自己决定说,以这个pixel为中心,哪些pixel是我们真正需要考虑的,那么些piexl是相关的,所以receptive field的范围不再是人工划定,而是机器自己学出来。
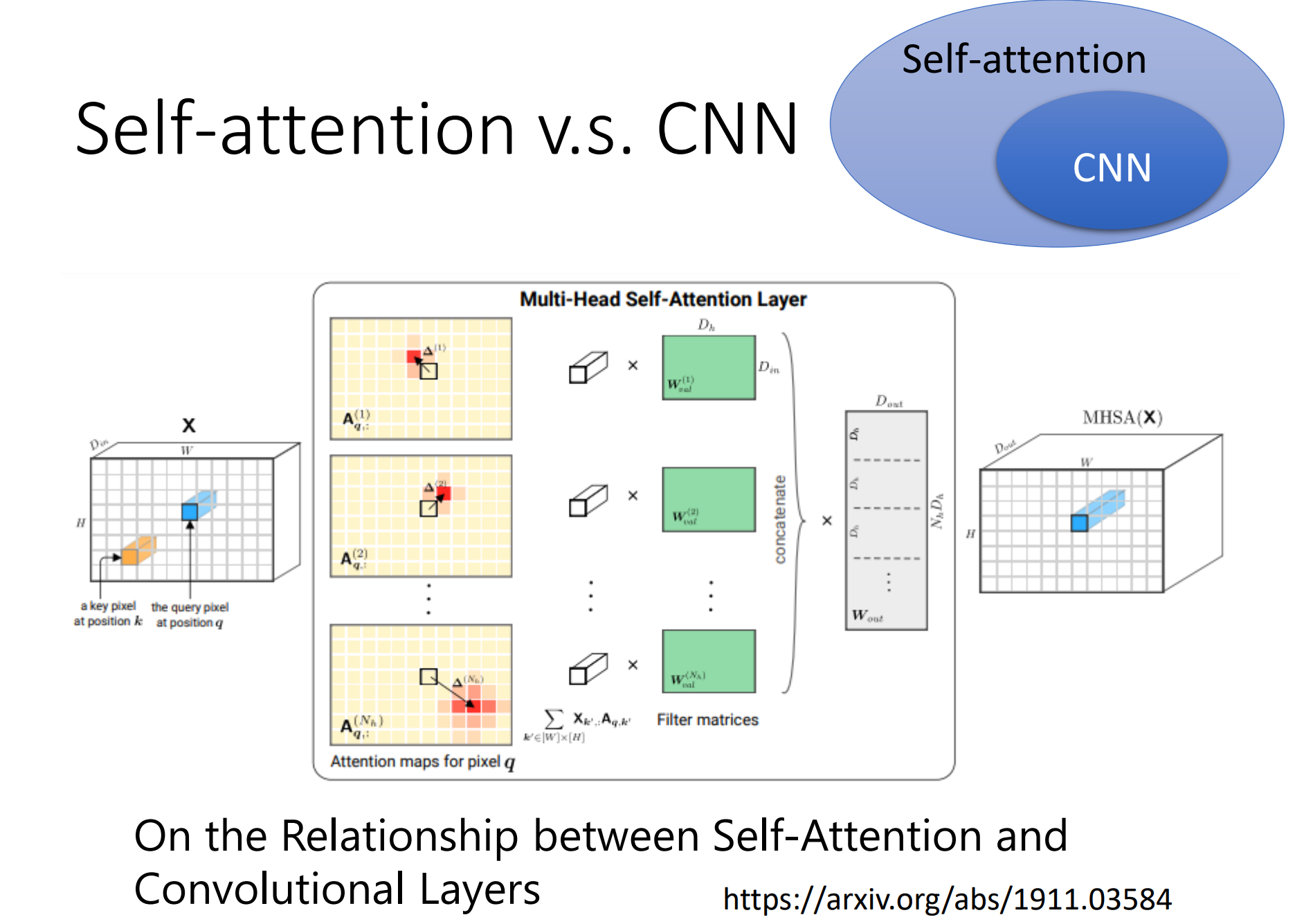
这边讲的是self-attention和CNN关系,其实你可以读一篇paper,这篇paper会用数学的方式严谨的告诉你说,其实这个CNN就是self-attention的特例,self-attention只要设定合适的参数,它可以做到跟CNN一模一样的事情。所以例如上图,CNN是self-attention的一个子集。
self-attention是更加flexible的CNN,而CNN是受限制的self-attention,self-attention只要透过某些限制,某些设计,它就会变成CNN。

既然CNN是self-attention的subset,self-attention比较flexible,那么我们再讲overfitting的时候,比较flexible的model,比较需要更多的data,如果data不够,那么就有可能出现overfitting;而小的model,比较有限制的model,它适合在data小,少的时候,它可能比较不会overfitting,如果这个限制设置的好,也会有不错的结果。
如果今天使用不同的data量来训练CNN跟self-attention,你确实可以看到上面说的现象。
对于Google来说比较小的资料量也是你没有办法用的资料量,这里10M就是最少的一个量,资料量比较大的setting有300M。 我们可以看到,随着data量越来越多,self-attention的结果就越来越好,最终在data量最多的时候,self-attention超过了CNN,但是在data量少的时候,CNN是可以超过self-attention。那为什么会这样,就可以从CNN和self-attention他们的弹性来加以解释。self-attention的弹性比较大,所以需要更加多的训练data,训练资料少的时候就会overfitting;而CNN弹性比较小,在data量少的时候可以有更好的泛化性。

其实这门课现在就不会讲到RNN,因为RNN的角色很大一部分可以用self-attention来取代了,所以在这门课是不会再特别把RNN拿出来讲。
RNN和self-attention一样,都是要处理input是一个sequence的情况。
上图是一个简易的RNN结构图。
那么self-attention和RNN有什么不同呢?当然一个非常显而易见的观察,就是self-attention是观察了整个sequence,而RNN只考虑了左边输入的vector没有考虑右边的vector,但是其实RNN也是可以双向的,如果是双向的RNN,那么也可以认为是考虑整个sequence。
self-attention相对于RNN的优势:
- 距离问题
对RNN来说,假设最右边黄色的vector要考虑最左边的这个input,那么就必须要把最左边的输入存在memory中,而且不能忘记,最终在最后一个时间点传到黄色的vector手上才能被考虑;而self-attention就不存在这个问题,主要这边输出一个query,这边输出一个key,只要它们可以match起来,天涯若比邻,你可以从非常远的vector,在整个sequence上非常远的vector轻易的抽取资讯。
- 并行问题
RNN是没有办法并行话的,而self-attention可以实现并行化。
所以现在很多应用都开始慢慢再把RNN换成self-attention。

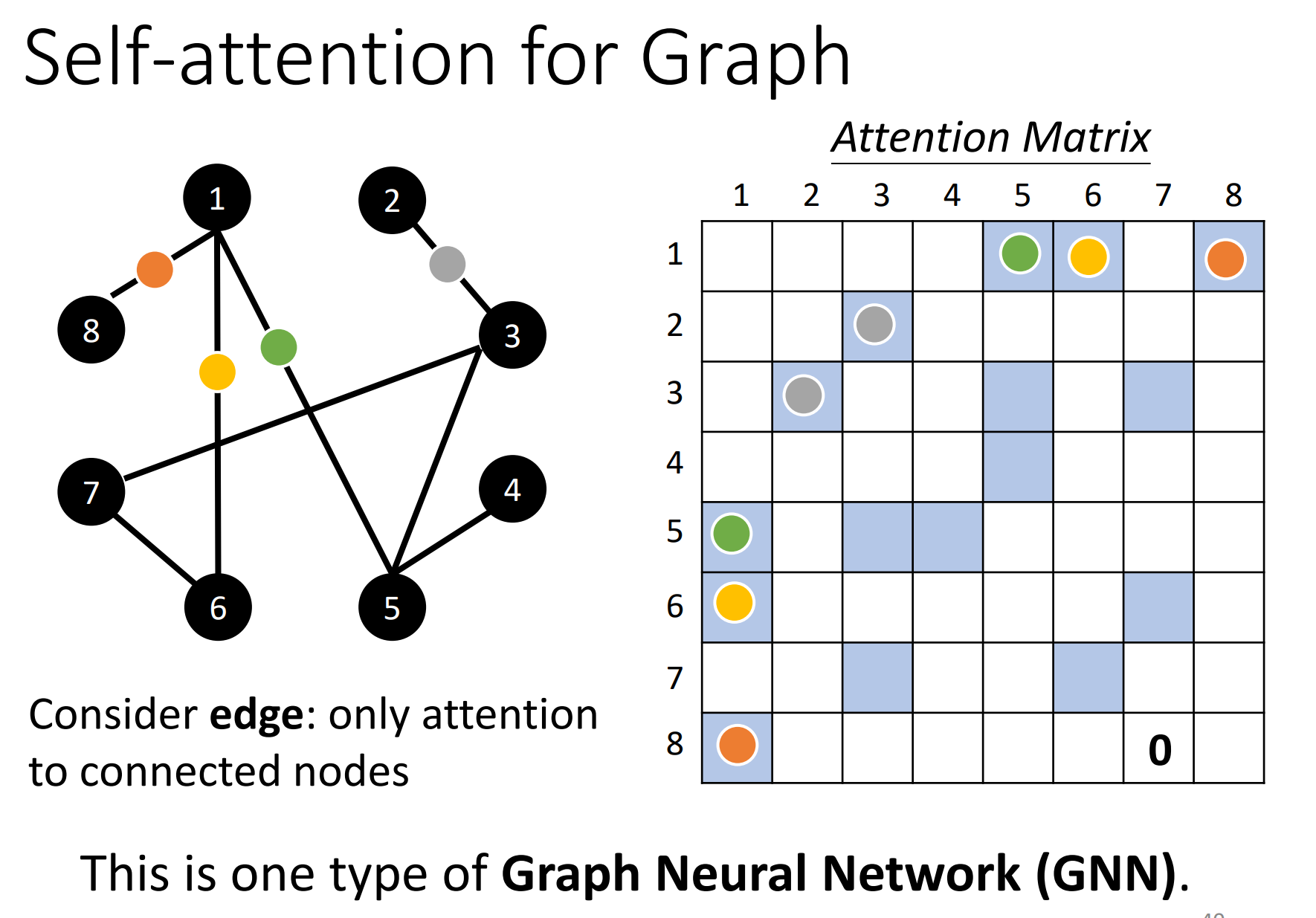
最后呢,self-attention也可以被应用在graph。
graph也可以看做是一堆vector,那么如果是一堆vector,就可以用self-attention处理。
在graph上面不只有node(一个node就是一个向量),还有edge,我们知道哪些node之间是有相连的,也就是哪些node是有关联的。之前我们在做self-attention的时候, 所谓关联性是network自己找出来的,但是现在既然有了graph的资讯,有了edge的资讯,那关联性也许就不需要透过机器自动找出来了,图上的edge已经暗示了我们node和node之间的关联性。所以今天当你把self-attention用在graph上面的时候,你有一个选择是在做attention matrix计算的时候,你可以只计算有edge向量的node就好,也就只要计算有edge相连的node之间的attention score。如果两个node之间没有edge,那么就可能暗示我们,这两个node之间没有关系,如果没有关系那么我们也就不用去计算这两个node之间attention score,直接设置为0就好了。因为这个graph往往是人为根据一些domain knowledge建立出来的,那domain knowledge告诉我们这两个向量彼此之间没有关联,我们也就没有必要再用机器去学这件事情。
那么其实当我们把self-attention按照上述限制用在graph的时候,其实就是一种GNN。其实GNN现在也是一个很fancy题目,那不会说self-attention就囊括了所有GNN各种变形,但把self-attention用在graph上面是一种类型的GNN。

这边GNN是没有办法细讲的,GNN这边坑很深呀,这里花了大概3小时讲GNN,但是其实也是没有讲完。
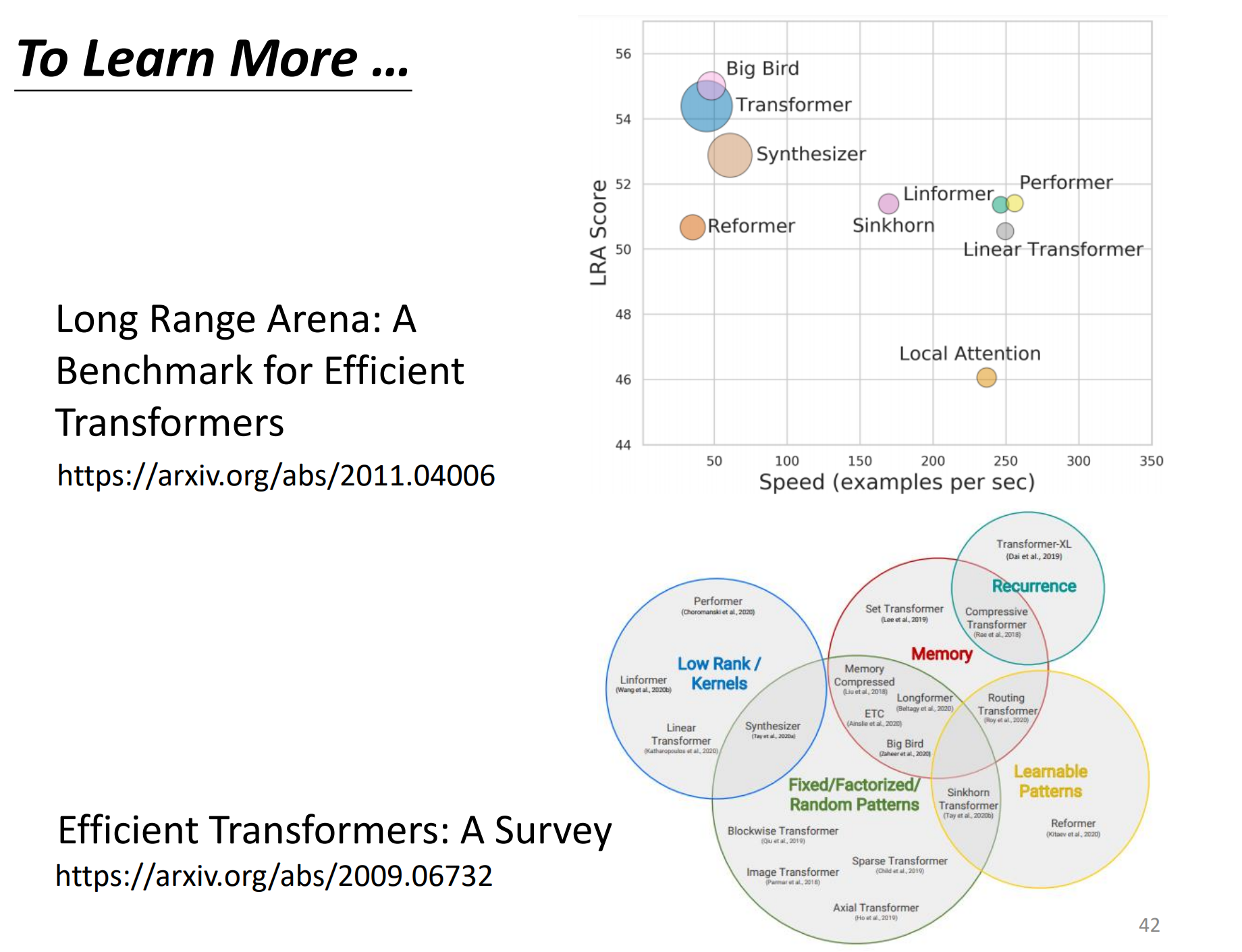
self-attention有非常非常多的变形。上面的paper比较了不同的self-attention的变形,因为self-attention的运算量非常的大,所以未来如何减少self-attention的计算量是一个重点。上图有各式各样的self-attention的变形,那self-attention最早使用在transformer上面的,所以很多人讲transformer的时候,其实就是指的这个self-attention,有人说广义的transformer指的就是self-attention,所以后面各式各样的self-attention的变形叫做xxx-former。 上面很多xxx-former的速度都会比transformer要快,但是精度就会差。什么样的self-attention又快又好,这仍然是一个尚待研究的问题。
代码
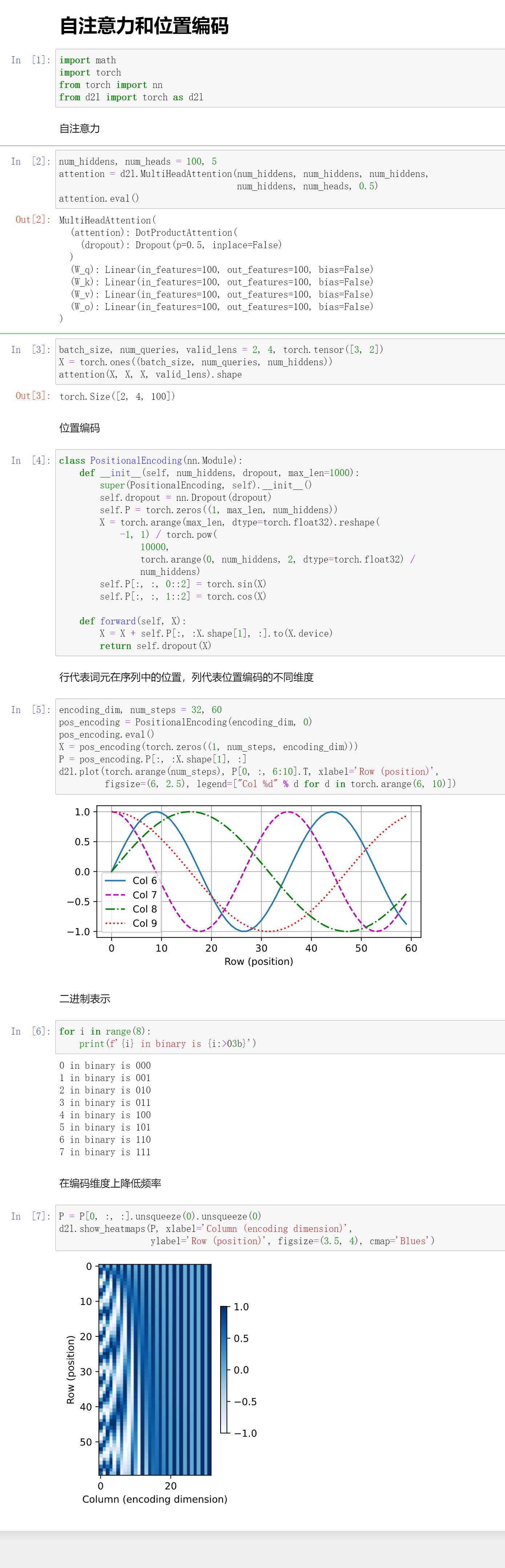
代码这里主要是展示了一个position encoding的实现。
QA
- 如果做阅读理解,比如把几个问题(比如主观题)作为query,把整片文章作为key/value,用注意力机制提取问题可能指向的段落或句子,可以实现吗?
可以的,这个就是一个QA系统,会在BERT的章节稍微讲一下。就是给模型阅读一段文本,我问你一个问题,你要能够根据文本来回答我。如果是答案在文本中,那么这个问题还是比较容易解决的;但是如果是答案不在文本中,然后需要推理的,就会相对困难。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号