动手学深度学习 | 数值稳定性+模型初始化和激活函数 | 12
数值稳定性

数值的稳定性,这个是机器学习中比较重要的一点,特别是当你的神经网络变的很深的时候,你的数值变的非常容易不稳定。

上面这里的t表示的层,而不是时间。\(h^{t-1}\)表示t-1层的输出。
这里的y还不是预测值,因为还多了一个损失函数。
向量对向量求导得到的一个矩阵,我们的主要问题就来自这个地方,因为我们做了太多的矩阵乘法。


这里是diag对角阵是因为向量x对自身的导数就是对角阵。


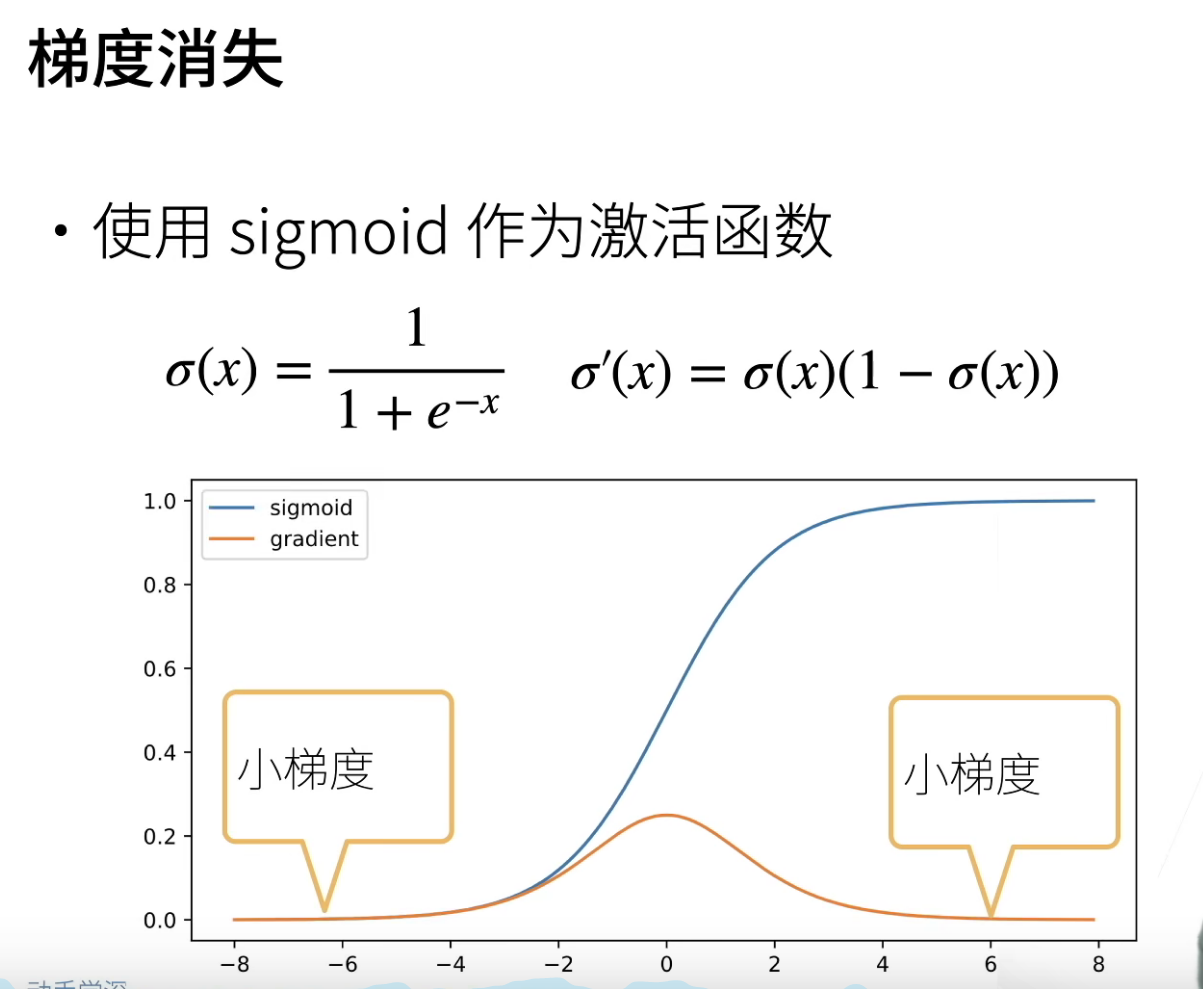


浮点数基本<5e-4的时候,那么就可以将其当做0来看待了。如果梯度为0,那么不管怎么学习,都是不会有进展的。
顶部可能就是一次矩阵乘法,但是如果一直乘乘乘就会让矩阵乘法变的特别的小,那么底部拿到的梯度就很小了,那么底部是训练不了的,导致无法使得网络加深。

模型初始化和激活函数

我们的一个核心问题是说,如何让训练更加稳定,就是梯度不要太大也不要太小。

有几种方法可以让训练更加稳定:
-
目标:让梯度值在合理的范围内 例如\([1e-6,1e3]\)
-
让乘法变加法 ResNet LSTM
不管是在CNN中使用比较多的ResNet,还是RNN中使用比较多的LSTM。
ResNet的核心是很多层的时候加入了加法进去。
传统的RNN如果输入一个句子,原始的时序神经网络就会对每个时序做乘法,太长就不行了,LSTM就是把这些乘法也变成加法。
不管是ResNet还是LSTM,都把100次的乘法变成100次的加法,加法当然出问题的概率就很小了。
- 归一化 梯度归一化、梯度裁剪
就是不管梯度是什么值,都会给拉回到均值为0,方差为1的这样一个分布;梯度裁剪就是如果梯度超过某个范围,那么就会舍弃超过范围的值
- 合理的权重初始和激活函数
\(w\)和\(\sigma\)还是有很大影响的。这是今天要讲解的重点。

就是不管哪个层的输出和梯度,都是希望均值为0,方差为a、b,那么网络做多深,我都可以保证数值在一个合理的范围内。


首先这里考虑的是均值。
i.i.d是独立同分布的意思,第t-1层的输入和第t层的权重是独立事件。
因为之前假设一层的\(E(w^t_{i,j})=0\),所以得到的第t层的输出的均值也为0。

均值的平方为0,等价于方差。
利用上面的\(E(h_i^t)=0\)的结论,我们可以得到\(Var(h_i^t)=n_{t-1}\gamma_tVar(h_j^{t-1})\),然后现在我们的目标是要输入的方差\(Var(h_j^{t-1})\)和输出的方差\(Var(h_i^t)\)是一样的,那么就可以推出\(n_{t-1}\gamma_t\)=1
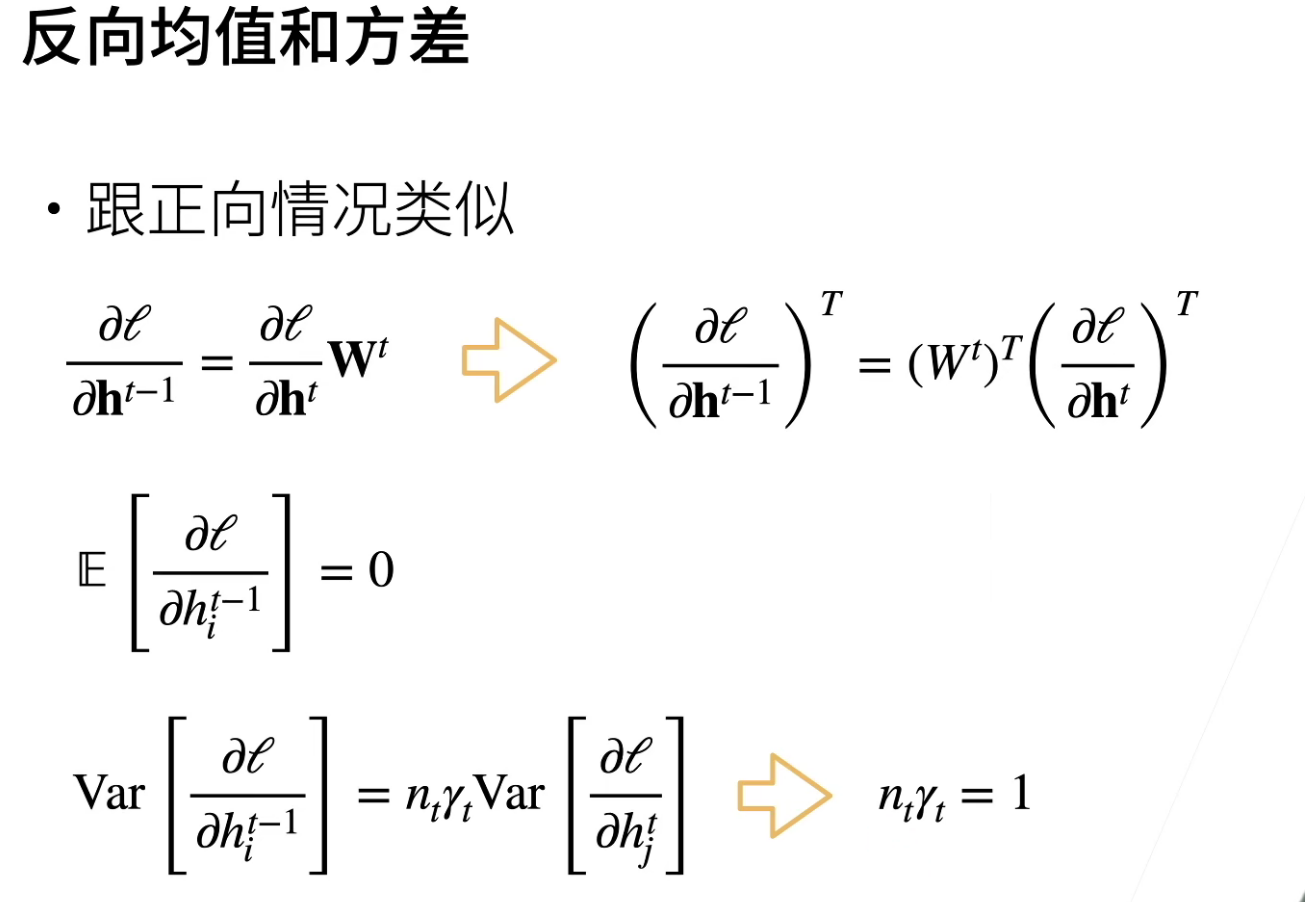
反向的话和正向是差不多的。

\(n_{t-1}\)表示第t层输出的维度,\(n_t\)是输出的维度。除非刚好输入维度等于输出维度 ,否则是无法满足\(n_{t-1}\gamma_t=1\)和\(n_{t}\gamma_t=1\)。
\(\gamma_t\)表示第t层权重的方差。
Xavier初始也是一个常用的权重初始化的方法,根据输入维度和输出维度来适配方差。

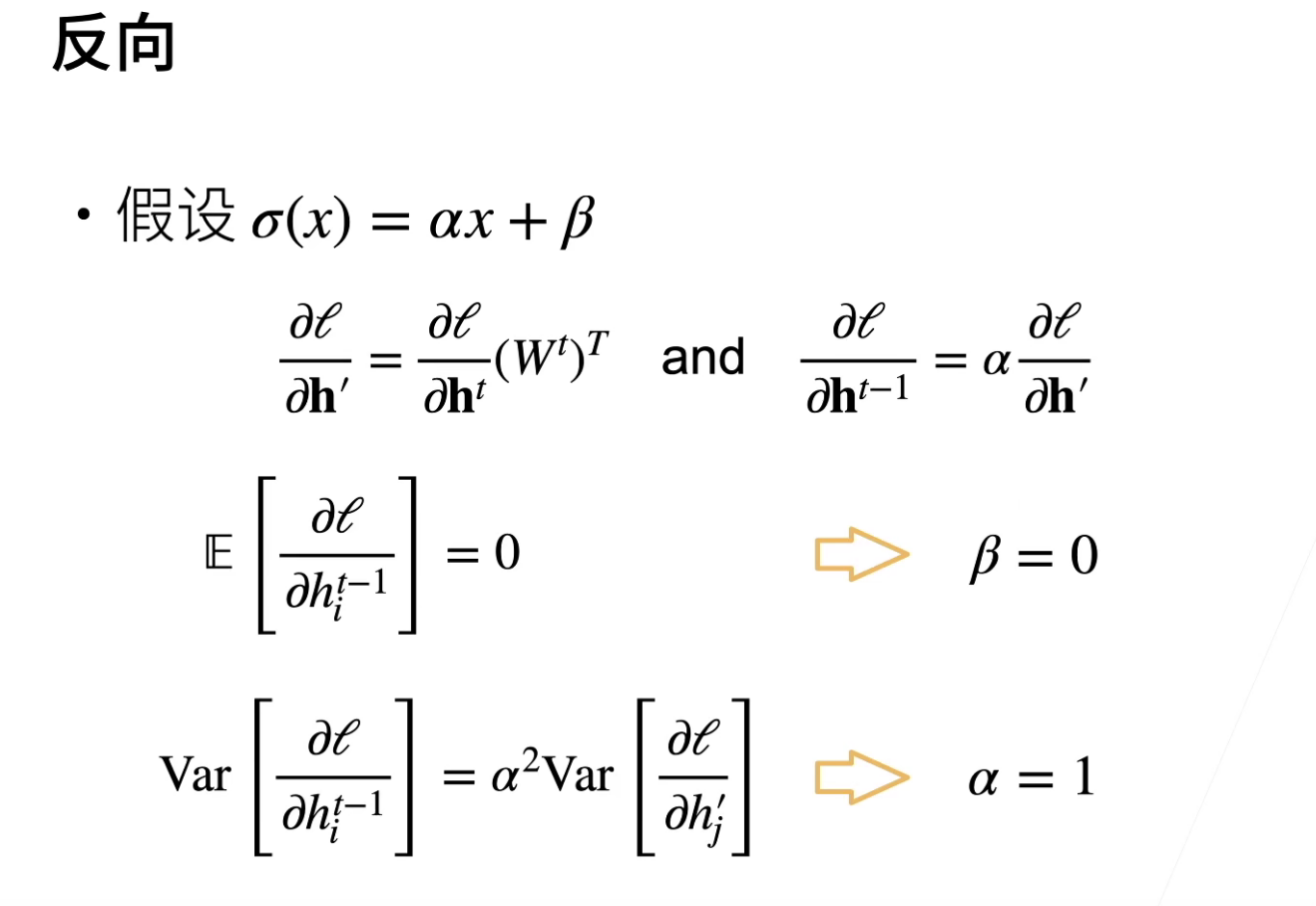
之前是没有激活函数的,现在加入一个线性激活函数,当然实际中是不会使用线性激活函数的,这里就是存粹就是为了推理方便。
这里假设激活函数\(\sigma=\alpha x+\beta\),结论就是如果要保证输入和输出的均值和方差保持一直,那么就要使得通过激活函数后,其输出的方差和均值不要改变,结论就是\(\beta=0,\alpha=1\)。
其实就意味着\(\sigma(x)=x\)。
其实就意味着\(\sigma(x)=x\)。
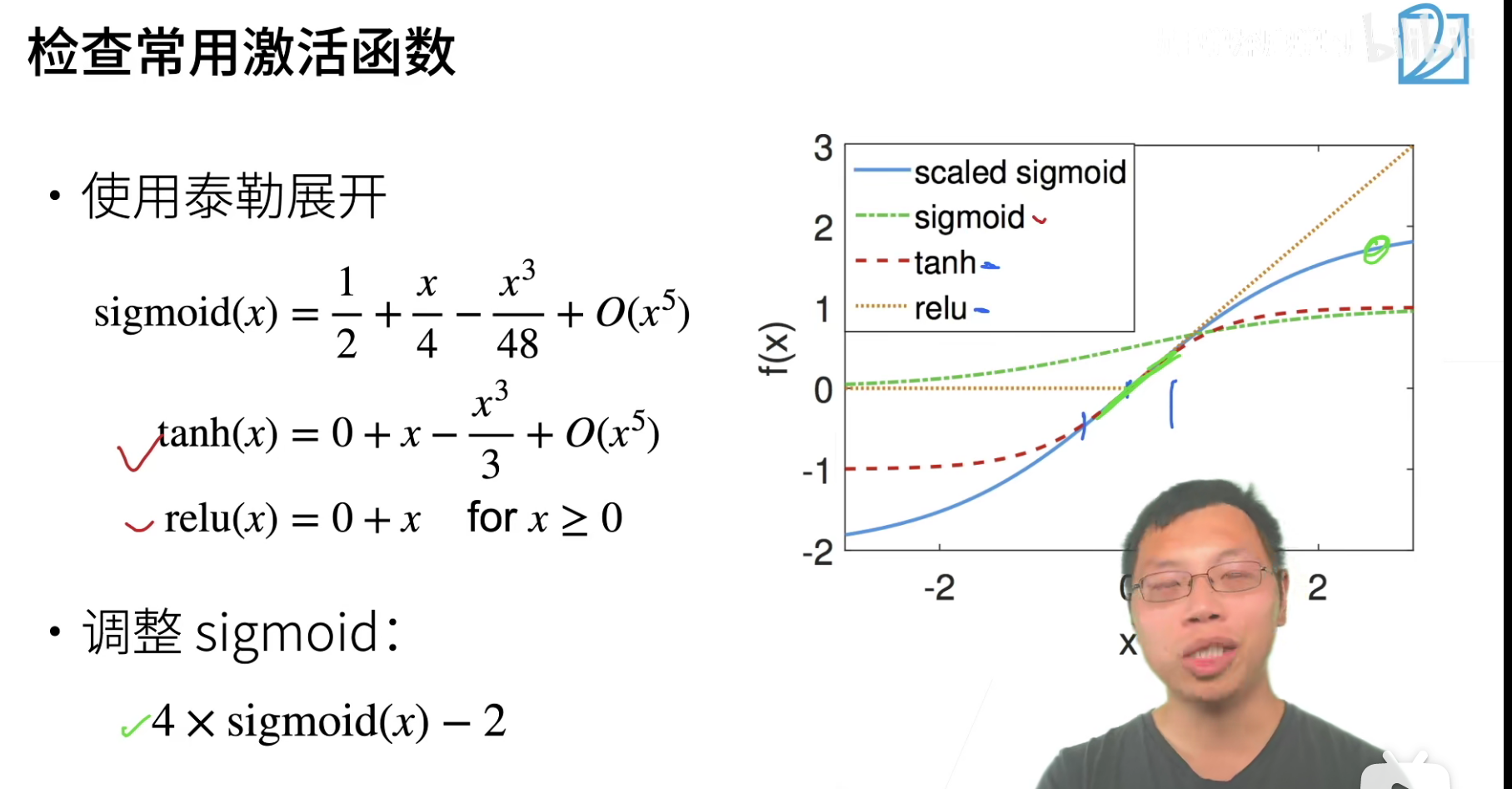
那么对于非线性的激活函数,可以使用泰勒展开,使用多项式去拟合。
tanh和relu在零点附近,确实近似到了一个\(f(x)=x\),而且神经网络权重通常也是一个在零点附近比较小的数,所以这两个函数问题是不大的, 至少在零点附近满足我们的要求。
sigmoid就不满足,因为sigmoid不过原点,所以要调整sigmoid为\(4 \times sigmoid(x)-2\)。像之前大家说的sigmoid说的那些梯度消失的问题,这个调整后的sigmoid基本都是可以解决的。
而且为什么tanh和relu效果不错,这是可以从数值稳定性这方面来进行解释。

合理的权重初始值和激活函数的选取可以提升数值稳定性,具体来说就是使得每一层的输出和梯度都是一个均值为0,方差为一个固定数的随机变量。
具体实现方法就是使用Xavier初始化和relu作为激活函数。
QA
- 关于梯度爆炸和梯度消失
ReLU容易梯度爆炸,sigmoid容易梯度消失。但是不能说sigmoid是引起梯度消失的罪魁祸首。
- 可以讲一下nan,inf是怎么产生以及怎么解决吗?
inf:就是数值太大了,通常来说就是lr调的太大造成的,或者是权重初始的初始值太大。
nan:一般就是除0,通常就是梯度已经很小了,然后又把梯度除0。
如何解决?
首先一个是保证数值稳定性:Xavier初始化权重 & 合适的激活函数。
然后一般lr都是尽量先往小的选(一般是0.003),然后直到inf和nan不出现了。
还有就是权重的初始,均值当然是为0了,然后方差也尽量小,一直往小调整,知道可以出来值,在慢慢调大,使得训练有进展。
- ReLU激活函数是如何做到拟合x平方或者三次方这种曲线的?
ReLU并没有去拟合曲线,拟合曲线是前面的“线性回归”去拟合的。激活函数的作用就是把这个线性给破坏掉。
而且ReLU是非线性的,它只是分段线性的, 一个函数是否满足线性需要满足\(f(ax+by)=af(x)+bf(y)\)
- 初学者,看不懂数学?怎么突破一下?
深度学习的好处就是让你不用懂数学也能够懂很多东西,传统的机器学习像SVM也好,你要优化或者什么你要有很多数学。神经网络只要可导就行了。
但是反过来说,虽然深度学习对数学的要求低了,但是这个东西你还是要学习的。
代码决定下限,数学决定上限。
- 输出或参数符合正态分布有利于学习,是有理论还是经验所得?
其实没有说一定是要正态分布,只是要权重在一个合理的范围。使用正态分布存粹就是因为在数学上比较好算。
- 随机初始化,有没有一种最好的、最推荐的概率分布来找到初始随机值?
我不知道什么是最好的,但是Xavier是不错的。
- 梯度归一化不就是batch normalization吗?
其实是不一样的,后面会来讲这个事情。
- 正态分布假设有什么缺陷吗?为什么看起来是万能的?
因为中心极限定理,最后的一切一切,都会变成正态分布。
- 一般权重是在每个epoch结束以后更新的吧?
不是的,是每个batch都会更新一次权重(小批量随机梯度下降,用小批量来近似估计整体样本),一个epoch后已经更新过很多次权重了。
- 我用的resnet,为什么还是会出现数值稳定性的问题?
当然会,resnet只是缓解了数值稳定性的问题,但是并没有解决。
可以认为整个深度学习的发展,都是在尝试解决这个数值稳定性的问题。
- 数值稳定稳定性可能是由模型结构引起的,您觉得孪生网络,两路输入不一样,是不是很可能引起数值不稳定?
这是一个很好的问题,你有两类不同的数据,比如文本和图片,文本进一个神经网络,图片进另外一个神经网络,最后我们要把它合起来。这里的问题是说文本数据和图片数据的区间不一样,那应该怎么处理?可能文本的输出很大,图片的输出很小,这时候有能多种办法,batch norm是我们可以做的事情。但是这一块通常来做的方法,是两头通过一个权重,文本加上一个权重,加上图片(图片不用权重没关系),然后调这个权重使得这两块比较一样。
我们大概会在style transformation样式迁移讲到这个,它也是有两路输入,两路会通过权重,然后使得两路的数值范围在差不多的范围内。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号