动手学深度学习 | 线性代数 | 03
线性代数
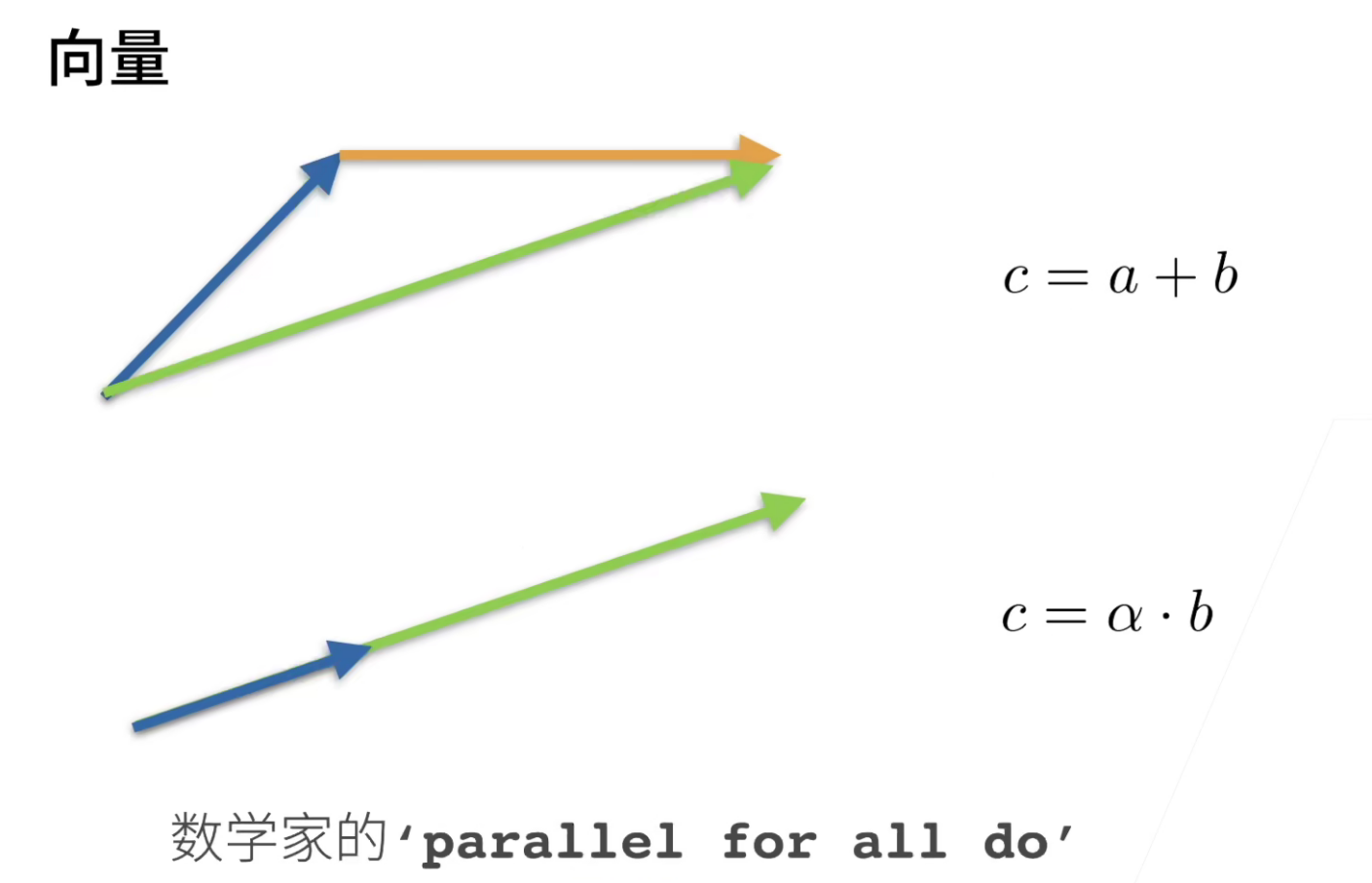
其实我们不需要太多线性代数的知识，但是还是稍微讲一下作为一个数学上的入门。
向量的距离使用 ||vecotr|| 来表示。
||a||2这个是L2范式，其实就是把向量里面的元素平方再求和，最后开方。
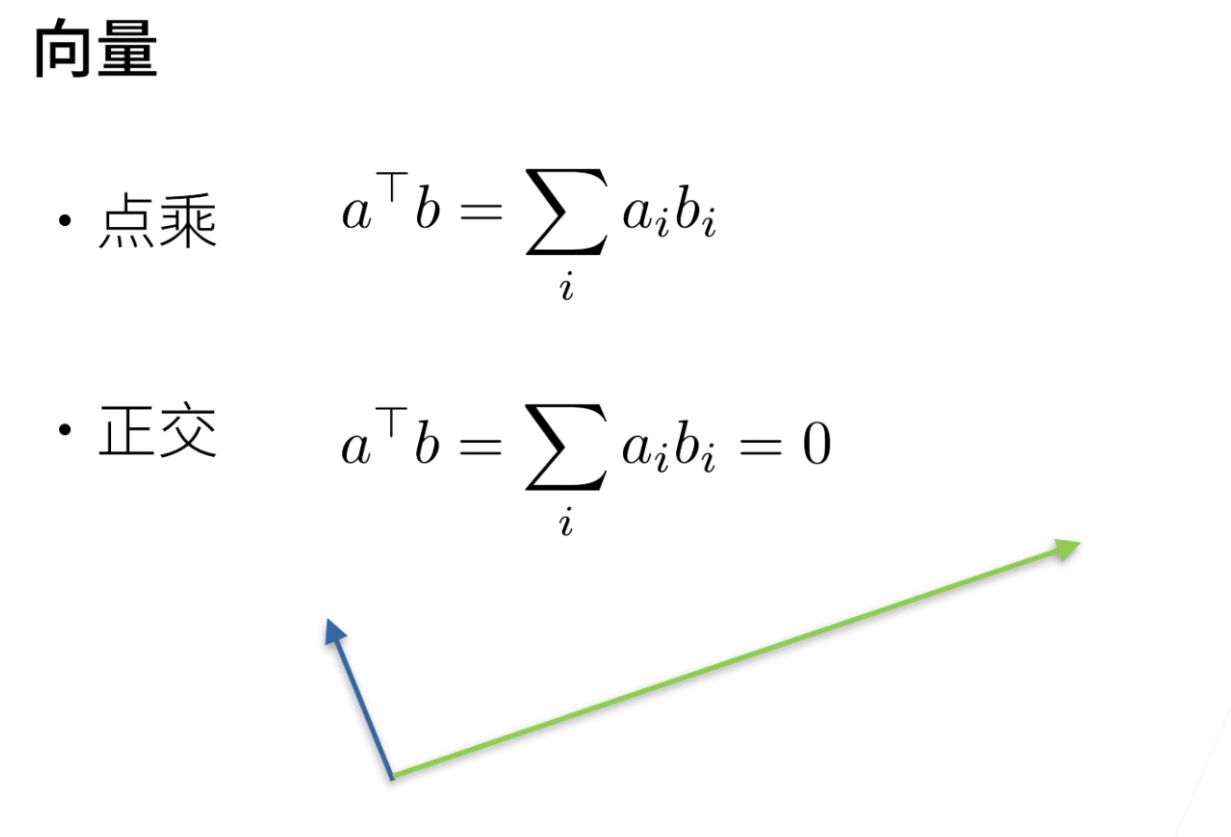
向量的点积： a^T b
向量的正交： a^T b = 0
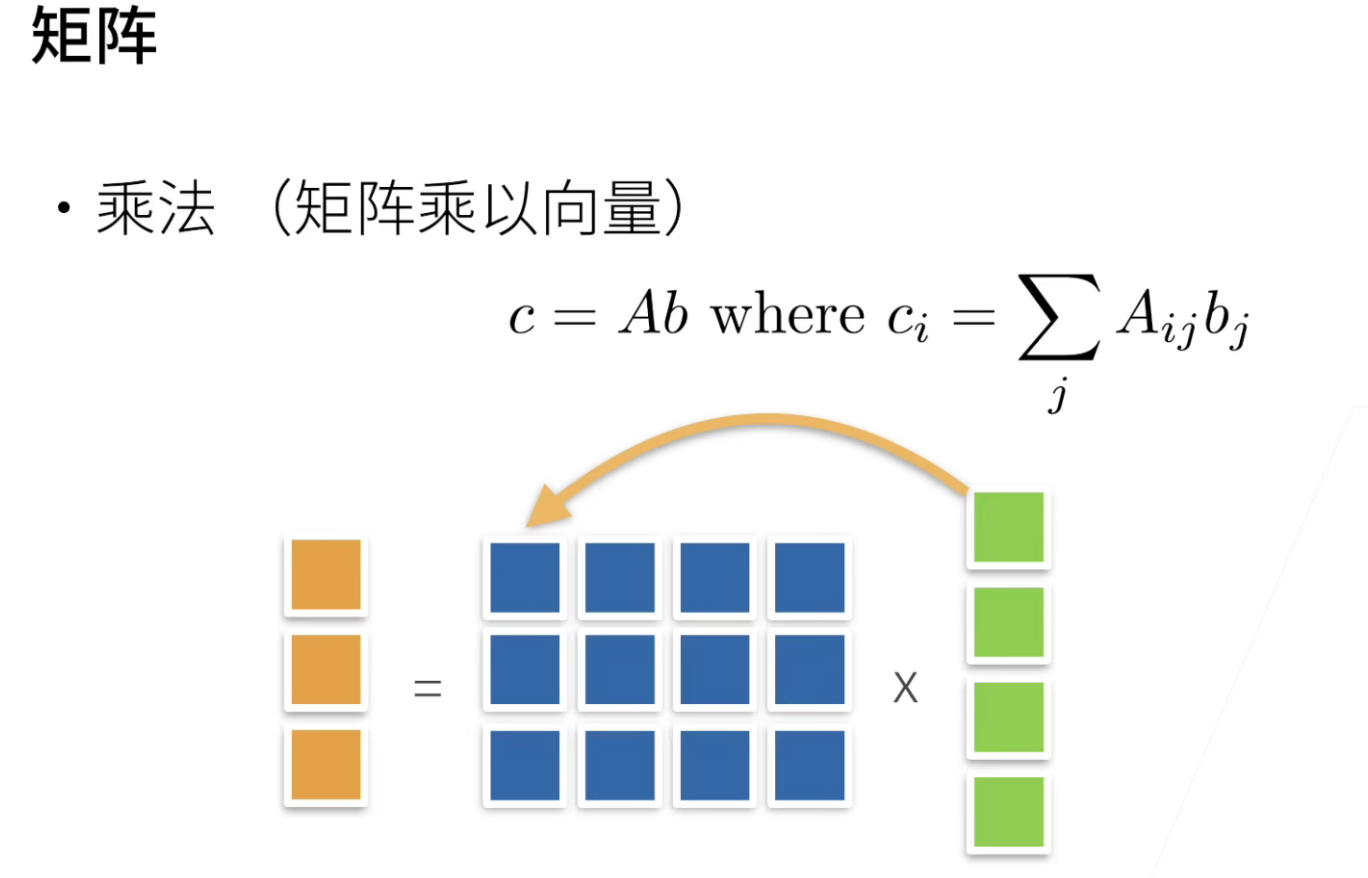
矩阵乘法，左边看行，右边看列（“左行右列”），一个一个元素相乘然后求和，最后填入一个新的shape的矩阵中。
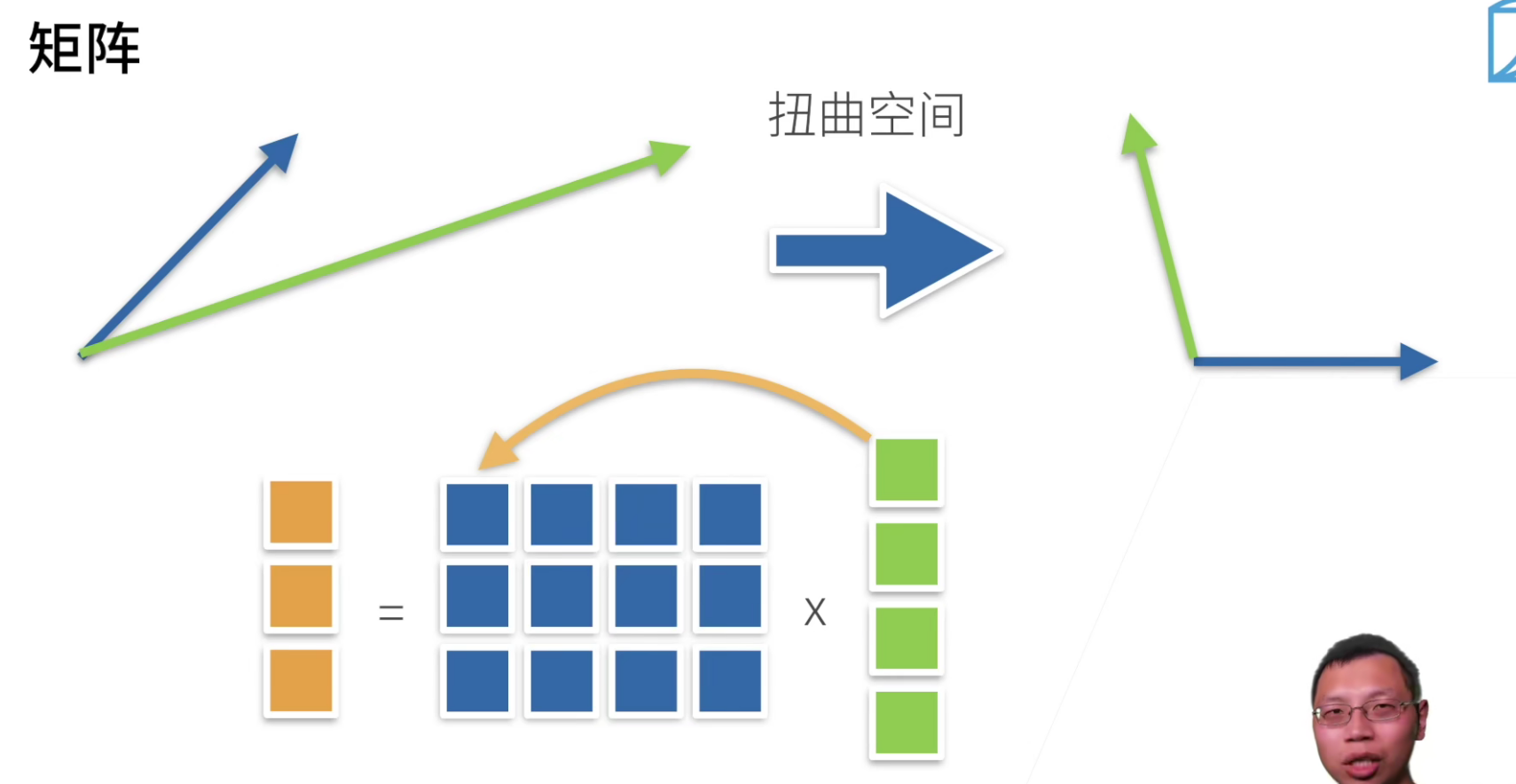
矩阵乘法从直观上来说，它是一个扭曲的空间。
一个向量通过一个矩阵乘法，变成一个另外的向量，这个矩阵其实是把一个空间进行了扭曲。
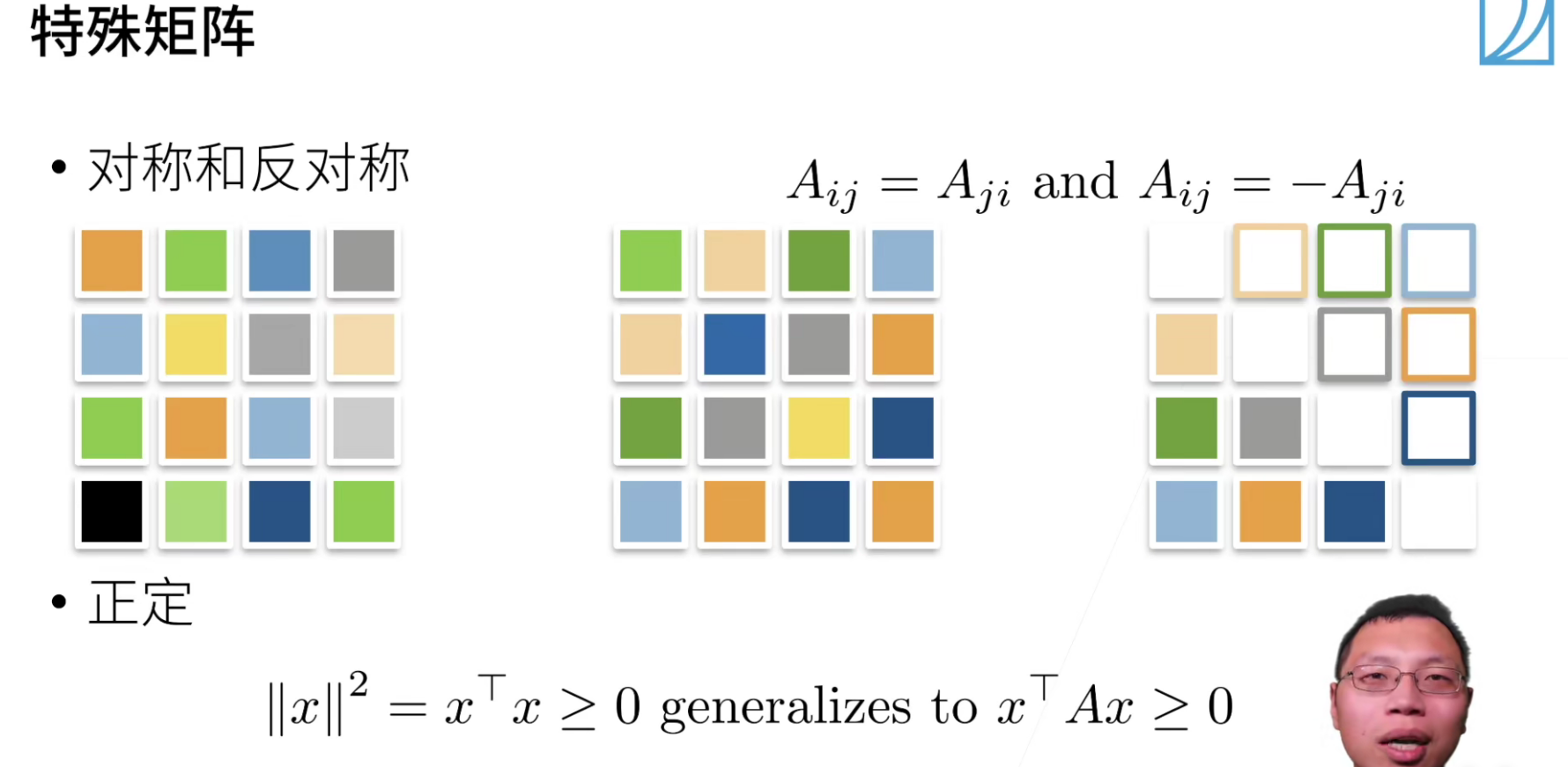
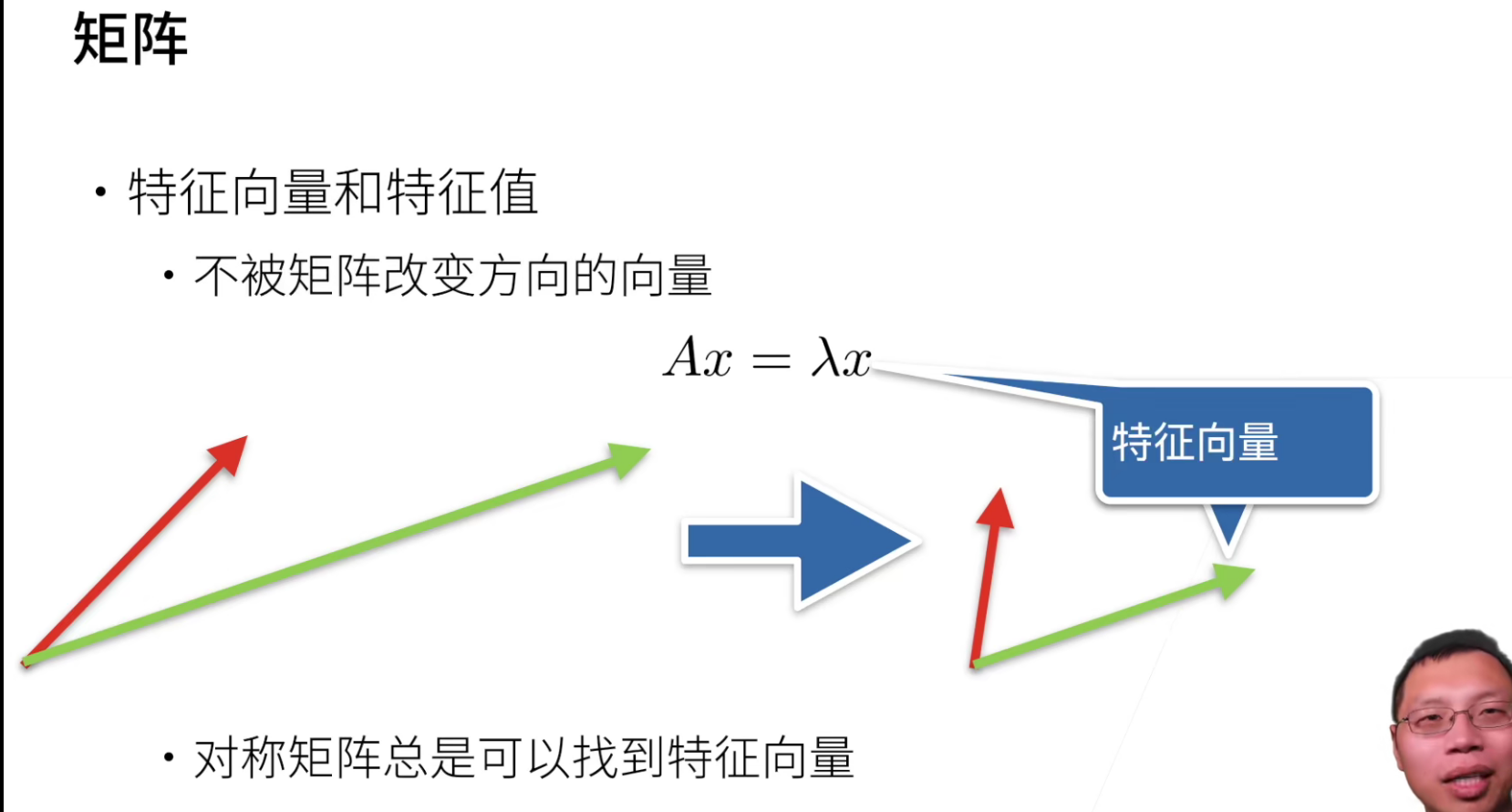
特征向量：不会被矩阵改变方向的向量
对称矩阵总是可以找到特征向量
上图中，红色的向量被方向改变了，绿色的向量方向没有改变，因此绿色的向量是特征向量（大小无所谓）
线性代数实现
操作总结
import torch
# 标量的表示
x = torch.tensor([3.0])
y = torch.tensor([2.0])
x + y, x * y, x / y, x**y
# 向量表示
x = torch.arange(4)
x[3] # 访问向量的元素
len(x) # 获取向量长度
x.shape # 获取向量的shape
# 创建一个矩阵
A = torch.arange(20).reshape(5,4)
A.T # 矩阵的转置
# 判断A是否是对称矩阵
A == A.T
# 多维矩阵
X = torch.arange(24).reshape(2,3,4)
A = torch.arange(20, dtype=torch.float32).reshape(5, 4)
B = A.clone() # 深度克隆一个矩阵
A, A + B
# axis=0 竖直方向
A_sum_axis0 = A.sum(axis=0)
A_sum_axis0, A_sum_axis0.shape
# axis=1 水平方向
A_sum_axis1 = A.sum(axis=1)
A_sum_axis1, A_sum_axis1.shape
# 按照两个维度求和，其实分两步做效果也是一样的
A.sum(axis=[0, 1])
# 求均值操作
A.mean(), A.sum() / A.numel()
# 竖直方向的求均值操作
A.mean(axis=0), A.sum(axis=0) / A.shape[0]
# 求和，但是不丢掉维度 keepdims=True
# keepdims就是为了方便使用广播机制
sum_A = A.sum(axis=1, keepdims=True)
A / sum_A # 利用广播机制进行相除
A.cumsum(axis=0) # 累计求和
torch.dot(x,y) # 向量的点乘
torch.mv(A,x) # 矩阵和向量的乘法
torch.mm(A,B) # 矩阵和矩阵相乘
# L2范数 torch.norm()
u = torch.tensor([3.0, -4.0])
torch.norm(u)
# L1范数 torch.abs().sum()
torch.abs(u).sum()
# F范数，其实就是矩阵的L2范数
torch.norm(torch.ones((4, 9)))
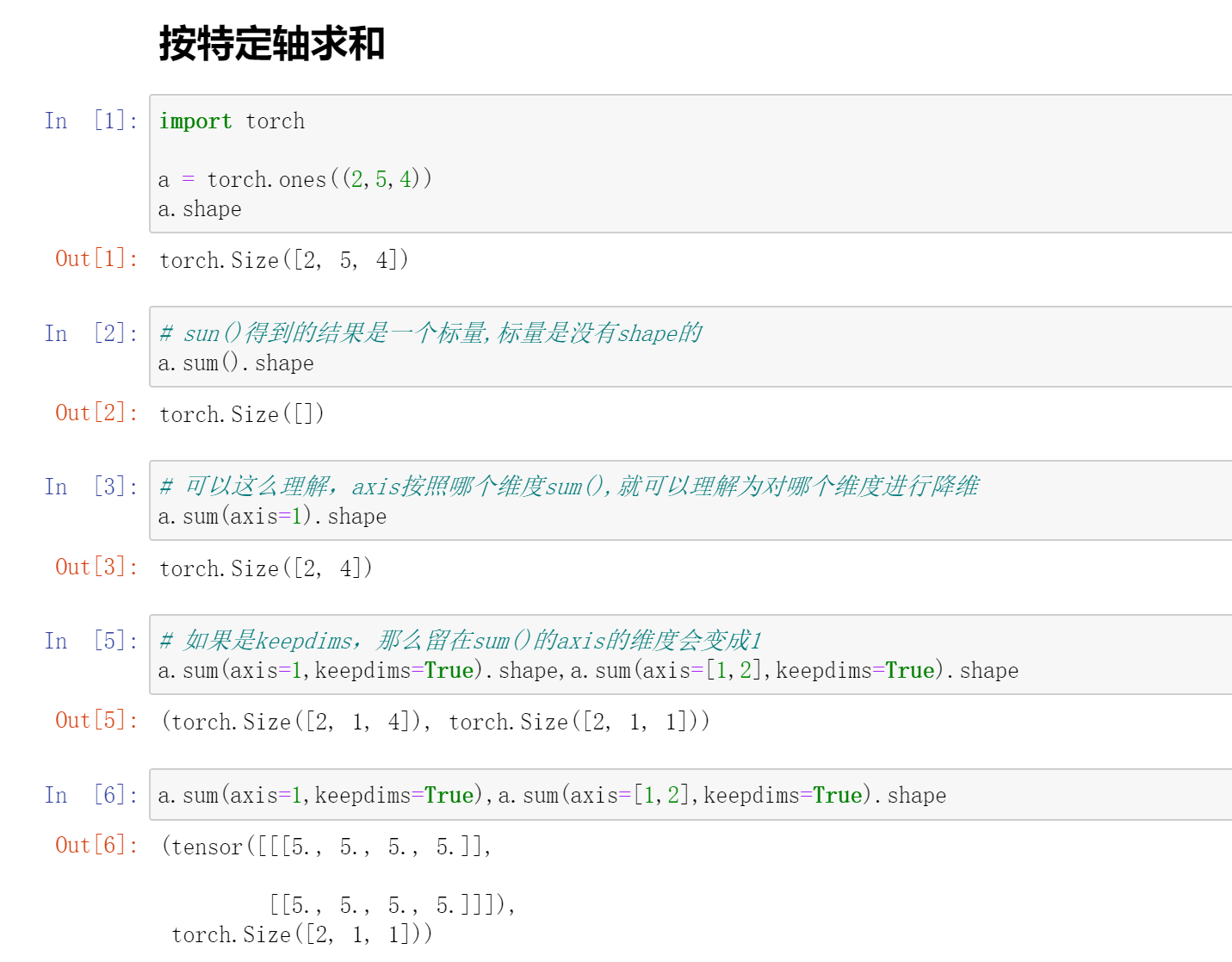
按特定轴求和
QA
- 将字符串进行one-hot编码有什么负面的影响吗？比如数值变得稀疏。
不会有什么负面影响，稀疏矩阵对于机器学习来说不会有影响。除了数据变得稀疏，比较耗费内存，其余并没有什么负面的影响。
- 对哪一维求和就是消除哪一维可以这么理解吗?
是的，可以这么理解。
- torch不区分行向量和列向量吗？
一般如果是一维的话，就是一个array，是不会进行严格区分的。
如果一定要区分行向量和列向量的，需要使用矩阵来进行区分，一个shape是(1,n)，一个shape是(n,1)
- sum(axis=[0,1])怎么求？
求和顺序，先求0再求1
