人脸识别智能小程序 | 深度学习基础 | 01
内容概况

卷积神经网络是深度学习汇中一种非常有代表性的网络结构,所以这里会先介绍一些深度学习的相关概念。
深度学习发展历程

人工神经网络的概念其实在50年代已经提出,但是受限于时代,不被重视。
06年Hinton提出,将多层感知机就命名为深度学习。
12年,Hinton的学习Alex设计提出AlexNet,在ImageNet的图像分类比赛中一鸣惊人,从此引爆了深度学习的热潮。
什么是人工神经网络?
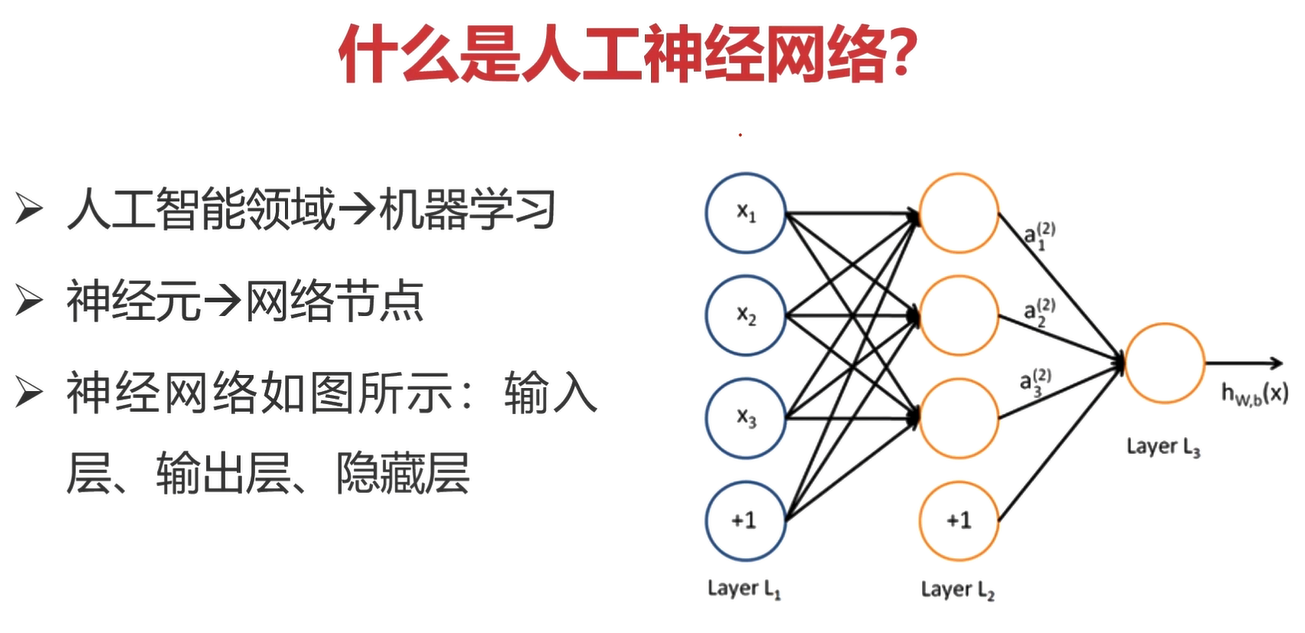
人工神经网络就是深度学习(06年Hinton说的),然后深度学习是机器学习的一种大类方法,和它同等地位的有类似聚类算法、支持向量机等。
如上图,图中一个一个圆圈就是一个一个神经元,多个神经元按照层次的形式组成神经网络。
神经网络的数据是按照层次结构从左向右流动的,依次可以划分输入层、隐藏层、输出层。
人工神经网络就是一个多层感知器模型。
什么是感知器?
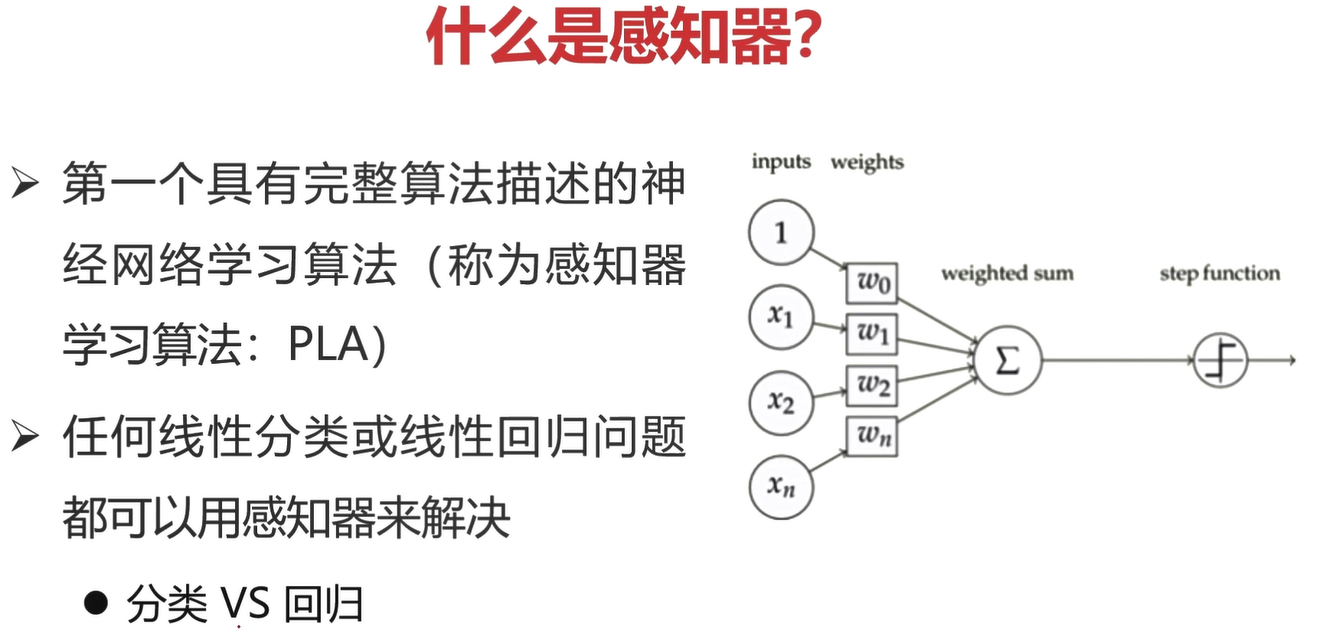
感知器
- 第一个具有完整算法描述的神经网络学习算法
- 任何线性分类或线性回归问题都可以使用感知器来解决
分类:预测的结果是离散值。
回归:预测的结果是连续值。
感知器可以理解为就是一个神经元!
从多层感知器到人工神经网络
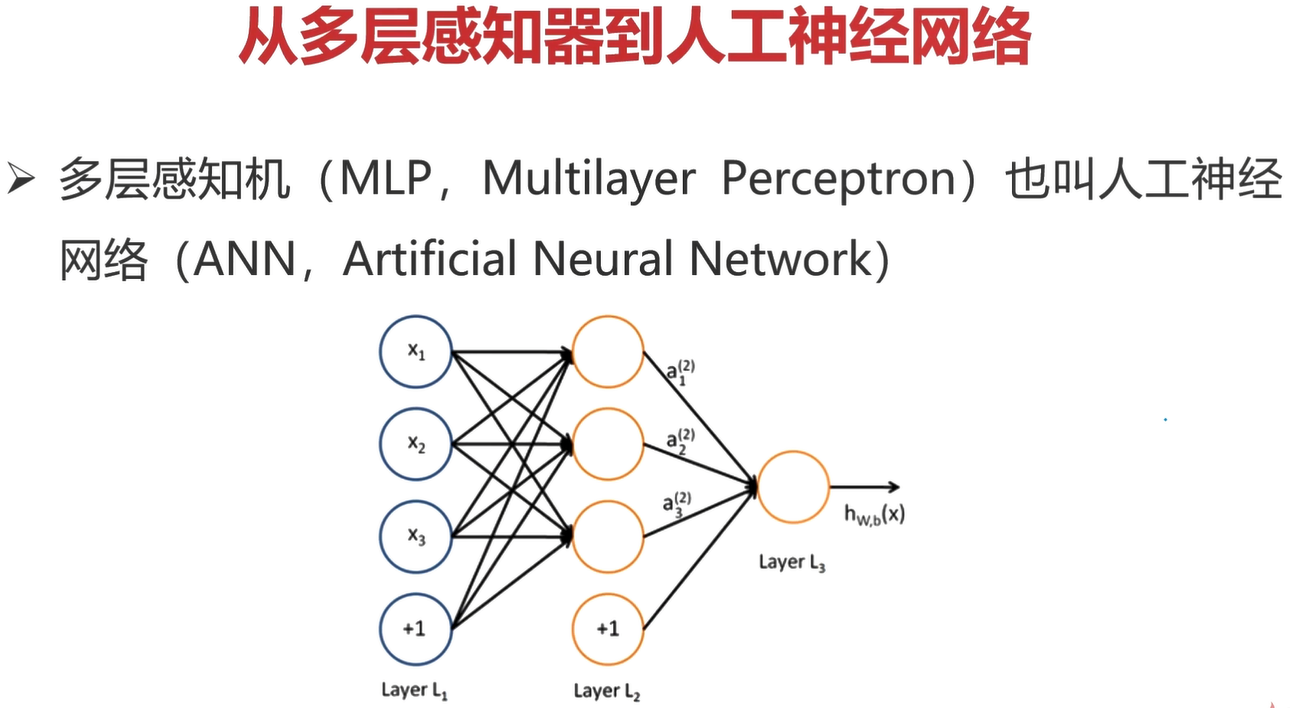

类似上图这么划分,可以把多层感知器划分成一个一个的单个感知器。
什么是深度学习?
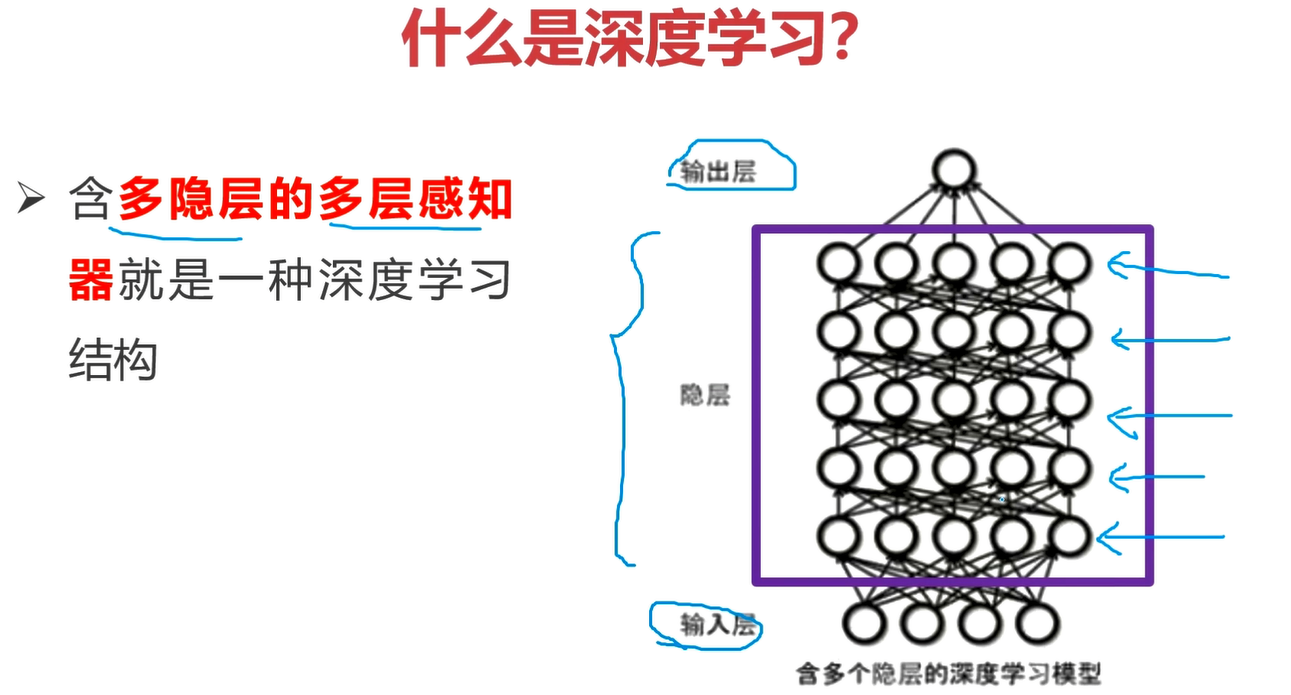
深度学习:含多隐层和多感知器就是一种深度学习结构。
深度学习其实就是人工神经网络中,有多个隐藏层,多个感知器。
如上图网络结构,隐藏层足够多,层数足够深,那么就可以归属于深度学习。
深度学习中的概念变迁总结

神经元(单层感知器)=》神经网络(多层感知器)=》含多隐层、多神经元的神经网络(深度学习)

前向运算:“怎么用“?也就是网络结构向前运算的过程。
反向传播:”怎么学“?也就是网络结构如何学习参数的过程。(有监督过程)
前向运算

前向计算:计算输出值的过程
不一定是线性进行运算,这个神经元的运算方式可以自己定义,但是这里以线性运算作为例子讲解。将处理的函数抽象为\(f(),g()\)
注意:\(w_{11},w_{12},...,b_1,b_2,...\)这些的取值都是不一致的(也有可能一样,但各自是独立的变量)
然后上图中的\(w,b\)是需要通过反向传播来计算的。
反向传播

反向传播:神经网络(参数模型)训练方法
- 解决神经网络的优化问题
- 计算输出层结果与真实值之间的偏差来进行逐层调节参数(梯度下降 自动)
BP算法是神经网路参数求解的一种算法,对于神经网络,参数的求解过程,也被称为“训练”。
神经网络的结构一般是人为先定义好,有多少层,每一层的结构具体是什么作用。但是每一层的具体参数是不知道的,那么就需要用到BP算法来帮助求解参数。训练的过程需要有标签的数据,所以神经网络也被称为有监督的算法。
神经网络=网络结构 + 参数
- 网络结构,人工设计的,规定好网络的层次,以及各层网络的作用,只需要规定好超参数
- 超参数:需要人工给定的参数
- 参数:BP算法求解
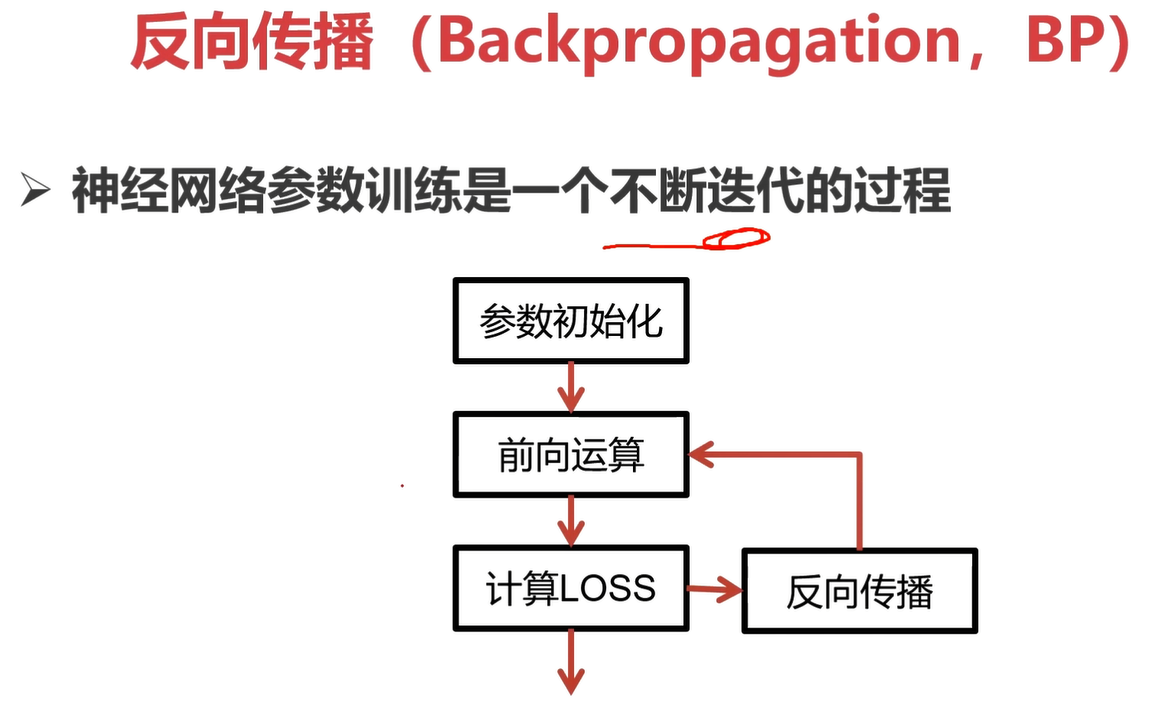
神经网络参数训练是一个不断迭代的过程。
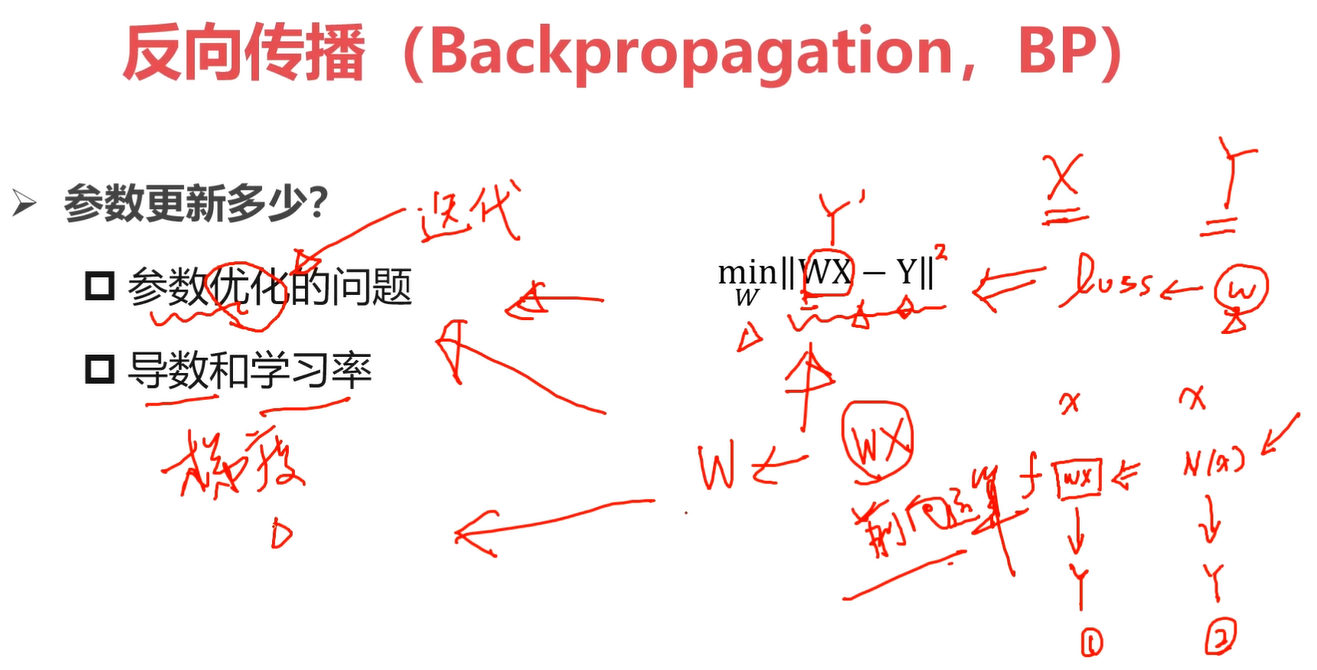
上图给出一个损失函数的例子\(loss(w,b)=min({|wx+b-y|}^2)\) 也就是\(w,b\)这两个是要优化求解的变量。
梯度下降法

导数:在一元函数中,可以理解为是变化率,是切线的斜率;在物理上可以理解为是瞬时速度,或是加速度。
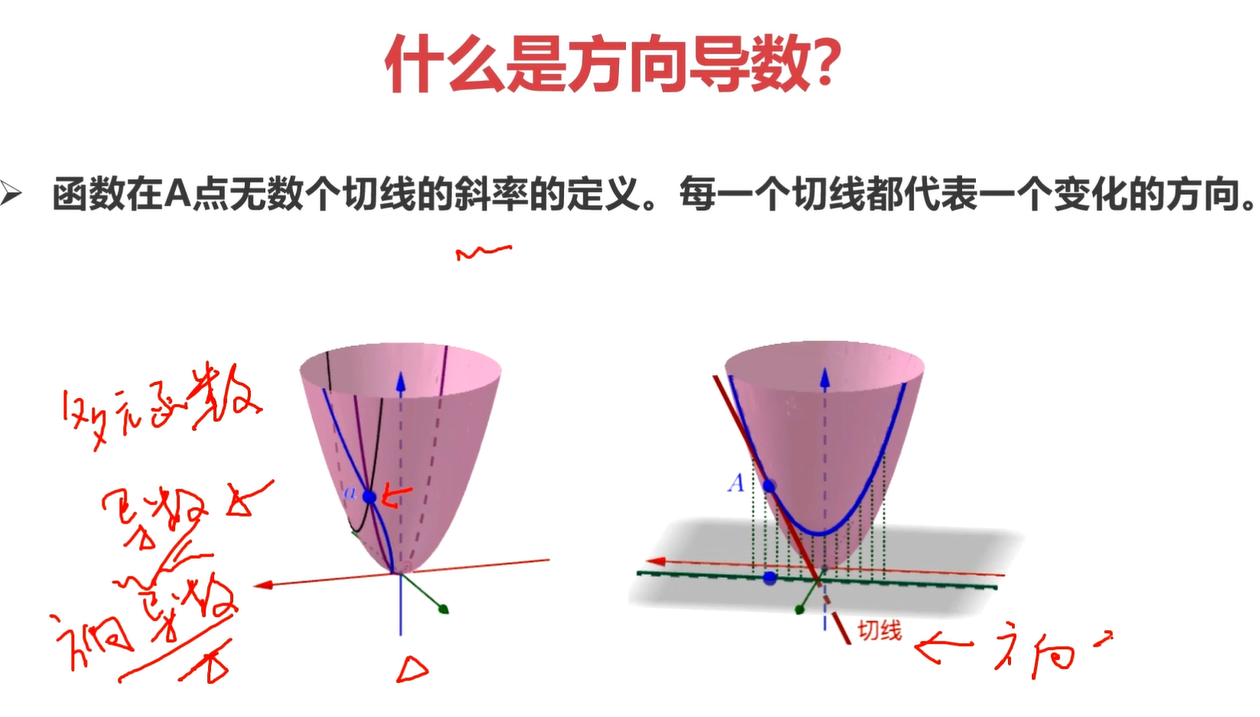
在多元函数(这里以三维为例子),一个点可以有无数条切线,所以为了描述这些各个方向的斜线的斜率,就有了方向导数的概念。过该点的每个方向的切线都有对应的方向导数。

偏导数:对多元函数进行降维。 比如把二元降维为一元。
理解偏导数对理解梯度下降算法有重要意义。
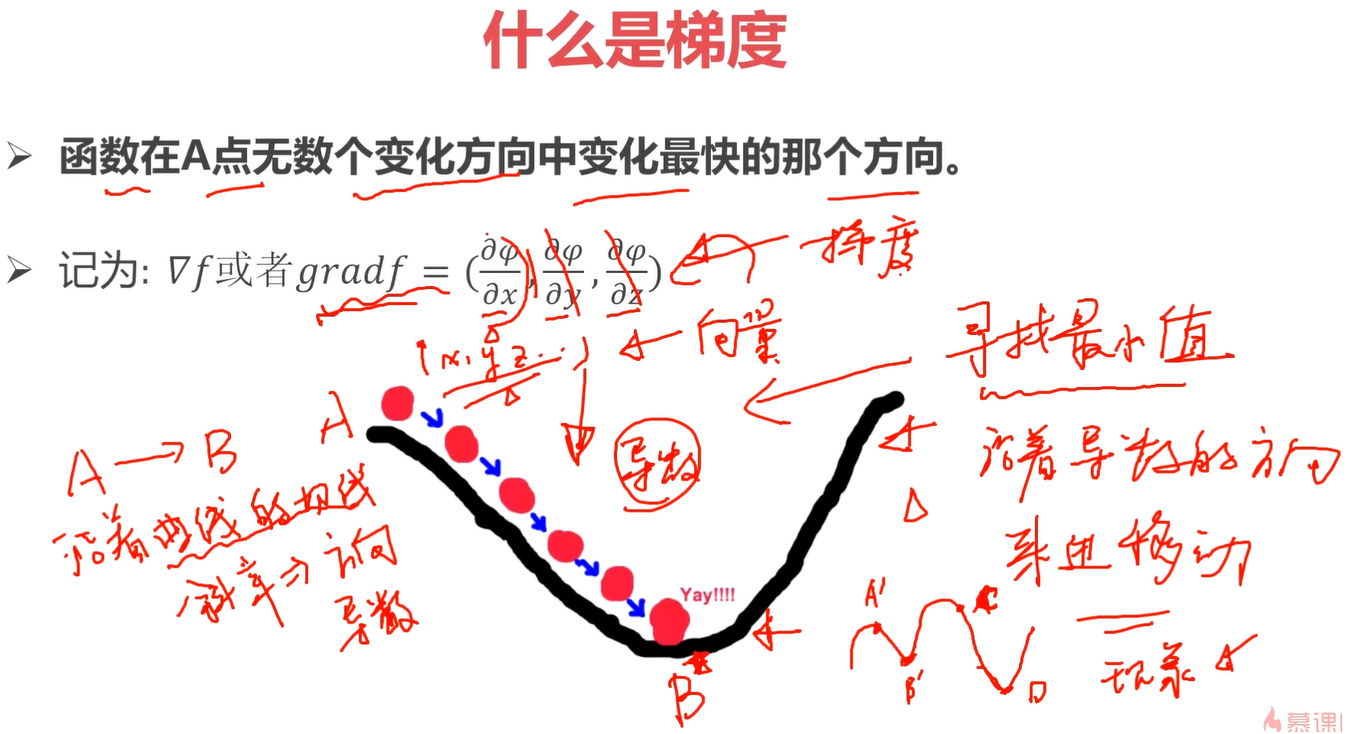
梯度:(在多元函数中)函数在A点无数个变化方向中变化最快的那个方向。
上图,A到B的过程,如果一直都是沿着切线的斜率方向(导数),那么就是到达B点最快的方式。那么该过程我们可以看作是一个寻找最小值的过程。
如果是一个非凸的函数,例如右下图有B,D两个最低点,如果是从A开始,那么找到的最低点就是B,如果从C开始,那么找到的最低点就是D。
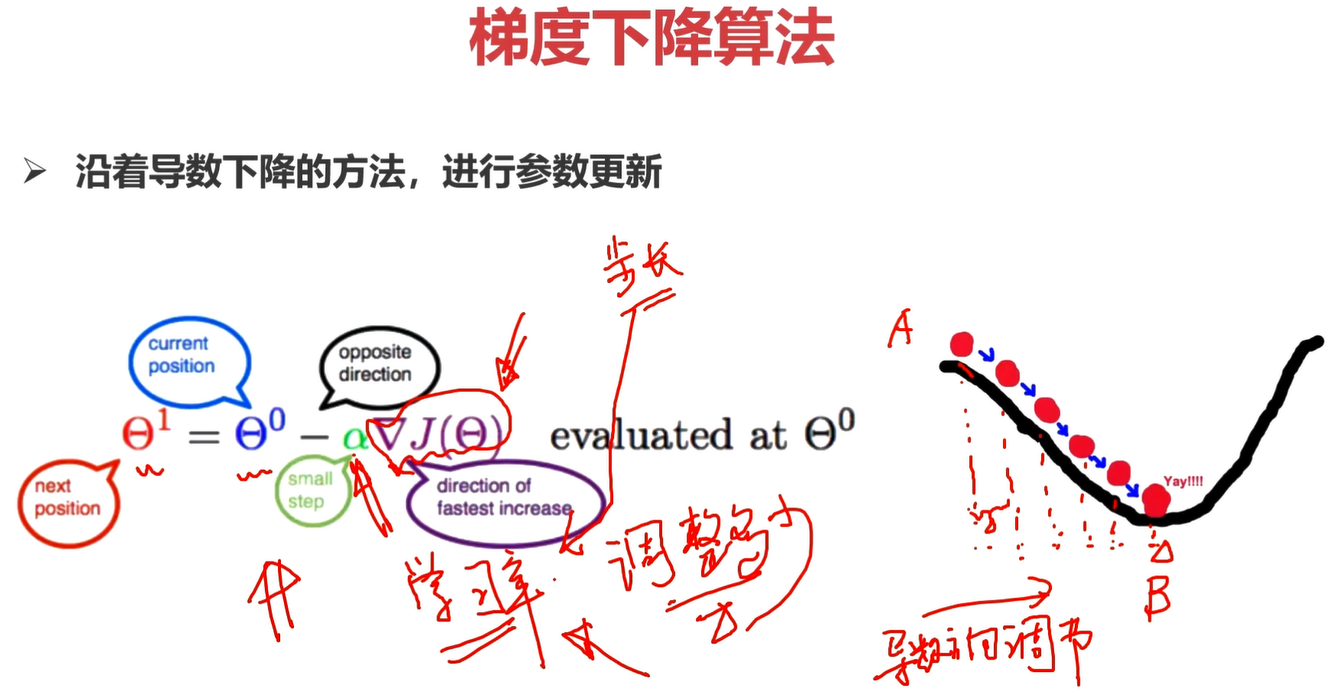
梯度下降算法:沿着导数下降的方法,进行参数更新。
具体形式化公式如上图所示,

选择合适的步长/学习率,是参数优化中非常重要的一点。
学习率过大,容易错过最优解;学习率过小,找到最优解需要很多步骤。
一般一开始的学习率设置会比较大,比如0.01,目的就是为了让模型快速收敛。伴随网络迭代的过程,逐步调节学习率,使得学习率逐步的变小,比如1w次迭代后,将学习率调整为0.001,然后再迭代1w次后,再调整学习率为0.0001。

非凸函数(函数中存在多个极值)最优化求解,一直是学术界和工业界非常难的问题。
通过梯度下降算法,并不能保证求解出来的解是最优的,有可能只是局部最优。
后面会讲解如何尽量保证最优解,这里不多做讨论。
深度学习发展迅猛的原因

常见深度学习模型

小结
什么是人工神经网络?
人工神经网络就是深度学习(06年Hinton说的),然后深度学习是机器学习的一种大类方法,和它同等地位的有类似聚类算法、支持向量机等。
人工神经网络就是一个多层感知器模型。
什么是感知器?
第一个具有完整算法描述的神经网络学习方法
任何线性分类或线性回归问题都可以用感知器来解决(牛逼!)
感知器可以理解为就是一个神经元!
分类和回归的概念
分类:预测的结果是离散值。
回归:预测的结果是连续值。
什么是深度学习?
深度学习:含**多隐层**和**多感知器**就是一种深度学习结构。
深度学习其实就是人工神经网络中,有多个隐藏层,多个感知器。
前向计算和反向传播(BP算法)
前向计算:计算输出值的过程
反向传播:确定网络参数的过程(一般指权值和偏置),BP算法是神经网络(参数模型)训练方法
**BP算法是神经网路参数求解的一种算法,对于神经网络,参数的求解过程,也被称为“训练”。**
机器学习的训练过程是指?
使用BP算法不断迭代优化参数的过程,就是机器学习的训练过程。
导数、方向导数、偏导数、梯度
导数:一元,切线的斜率(在一元情况下,导数就是梯度)
方向导数:多元,过A点的切线有无数条,每个方向过A点的斜率叫做方向导数
偏导数:对多元函数进行降维
梯度:多元,过A点无数个方向中变化最快的那个方向
梯度下降算法、学习率、局部最优
梯度下降算法:沿着导数下降的方法,进行参数更新。
选择合适的步长/学习率,是参数优化中非常重要的一点。
学习率过大,容易错过最优解;学习率过小,找到最优解需要很多步骤。
非凸函数(函数中存在多个极值)最优化求解,一直是学术界和工业界非常难的问题。
通过梯度下降算法,并不能保证求解出来的解是最优的,有可能只是局部最优。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号