机器学习听课 | Numpy | 03

目录

• Numpy的优势
  • Numpy介绍
  • ndarray介绍
  • ndarray与python原生list运算效率对比
  • ndarray的优势
• N维数组 -- ndarray
  • ndarray的属性
  • ndarray的形状
  • ndarray的类型
• 基本操作
  • 生成数组的方法
    • 生成0和1的数组
  • 从现有数组生成
    • 生成方式
  • 生成固定范围的数组
  • 生成随机数组
    • 均匀分布
    • 正态分布
      • 什么是正态分布
      • 正态分布的应用
      • 标准差与方差的意义
      • 正态分布的创建方式
    • 均匀分布和正态分布
  • 数组的索引,切片
  • 形状修改
  • 类型修改
  • 数组去重
• ndarray运算
  • 逻辑运算
  • 通用判断函数
  • np.where(三元运算符)
  • 统计运算
    • 统计指标
    • 案例: 股票涨跌幅统计运算
• 数学: 矩阵
  • 矩阵和向量
    • 矩阵
    • 向量
  • 加法和标量乘法
  • 矩阵向量乘法
  • 矩阵乘法
  • 矩阵乘法的性质
  • 逆,转置
• 数组间的运算
  • 场景
  • 数组与数的运算
  • 数组与数组的运算
  • 广播机制
  • 矩阵运算

Numpy的优势

Numpy介绍

Numpy(Numerical Python)是一个开源的Python科学计算库,用于快速处理任意维度的数组.
Numpy支持常见的数组和矩阵操作.
对于同样的计算任务,使用numpy比直接使用python要简洁的多.

numpy使用ndarray对象来处理多维数组,该对象是一个快速而灵活的大数据容器.

ndarray介绍

numpy提供了一个N维数组类型ndarray,它描述相同类型的"items"的集合.

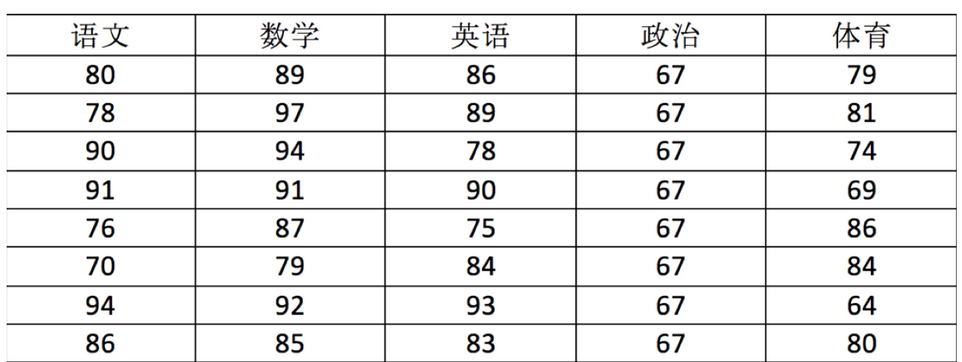
用ndarray存储上图数据:

ndarray与python原生list运算效率对比

在下面我们通过一段代码运行来体会ndarray的好处.

import random
import time
import numpy as np
a = []
for i in range(100000000):
    a.append(random.random())

# 通过%time魔法方法, 查看当前行的代码运行一次所花费的时间
%time sum1=sum(a)

b=np.array(a)

%time sum2=np.sum(b)

从上面我们可以看到ndarray的计算速度要快很多,节约了时间.
机器学习的最大特点就是大量的数据运算,如果没有一个快速的解决方法,那可能现在python在机器学习领域也达不到好的效果.
numpy专门针对针对ndarray的操作和运算进行了设计,所有数组的存储效率和输入输出性能远优于python的嵌套列表,数组越大,numpy的优势就越明显.

ndarray的优势

(1) 内存块风格
list: 分离式存储(存储是地址,不是数值),存储内容多样化
ndarray: 一体式存储,存储类型必须是一样的
(2) ndarray支持并行化运算(向量化运算)
(3) ndarray底层使用C语言写的,效率更高,释放了GIL

N维数组 -- ndarray

ndarray的属性

数组属性反映了数组本身固有的信息.

ndarray的形状

如何理解二维,三维,四维的数据呢?
二维就是一张Excel表,三维就是多张sheet叠加在一起,四维就是是多个Excel工作簿叠加.
五维后面就不好具象化了...

形状(2,2,3)应该如何理解?
从高维到低纬,有2块,2行,3列.

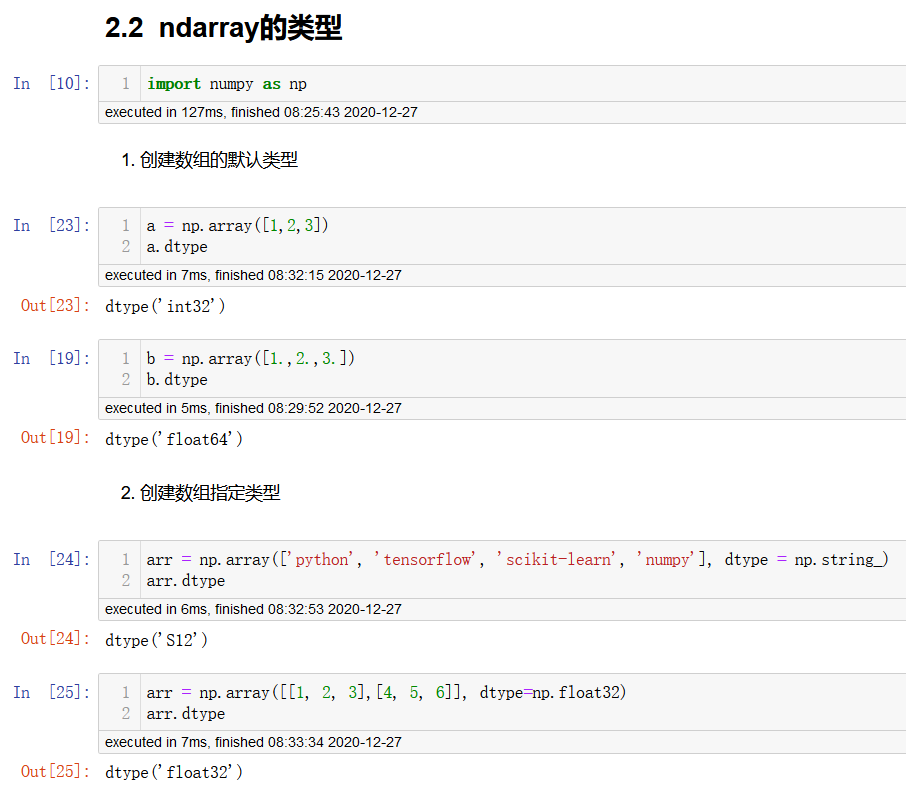
ndarray的类型

接下来看看numpy数组有哪些类型

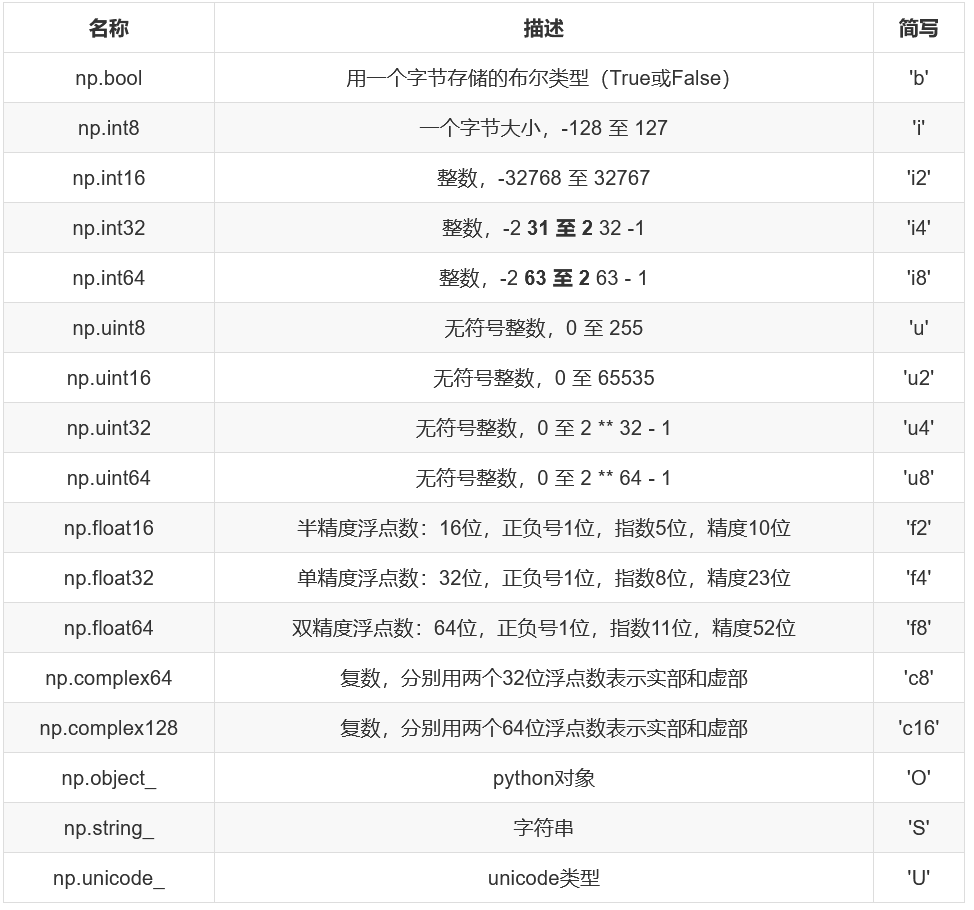
创建数组的时候指定类型

np.array(列表,dtype=...)
# 创建指定类型的数组

注意: 若不指定类型,整数默认为int32,小数默认float64

python类型   numpy类型
np.int == np.int32
np.float == np.float64
np.str == np.unicode_
np.bool == np.bool
np.object == np.object_

基本操作

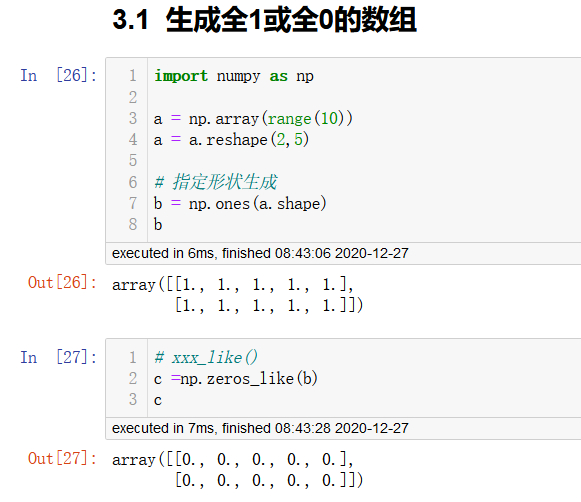
生成数组的方法

生成0和1的数组

# 生成全1的数组
np.ones(shape)
np.ones_like(a)

# 生成全0的数组
np.zeros(shape)
np.zeros(a)

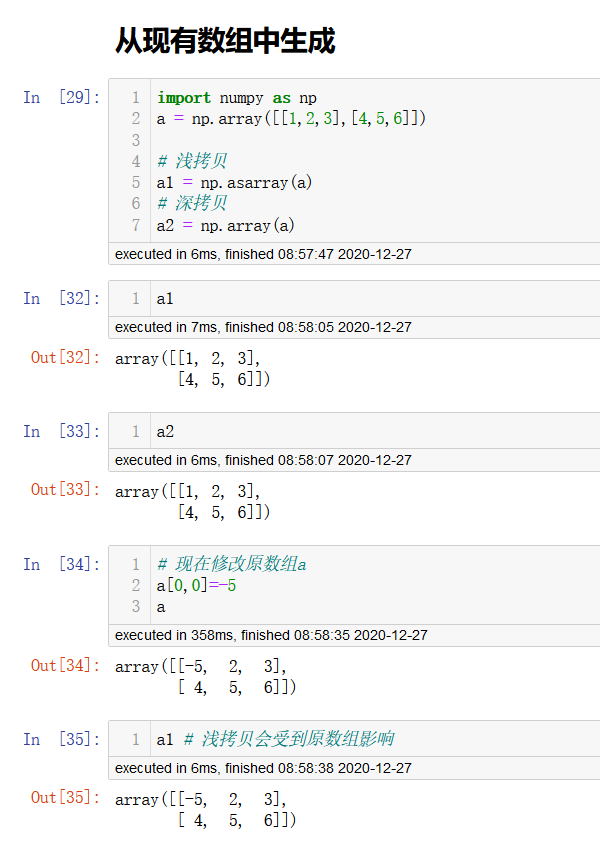
从现有数组生成

生成方式

np.array(序列) # 深拷贝
np.asarray(序列) # 浅拷贝

a = np.array([[1,2,3],[4,5,6]])
# 从现有的数组当中创建
a1 = np.array(a)
# 相当于索引的形式，并没有真正的创建一个新的
a2 = np.asarray(a)

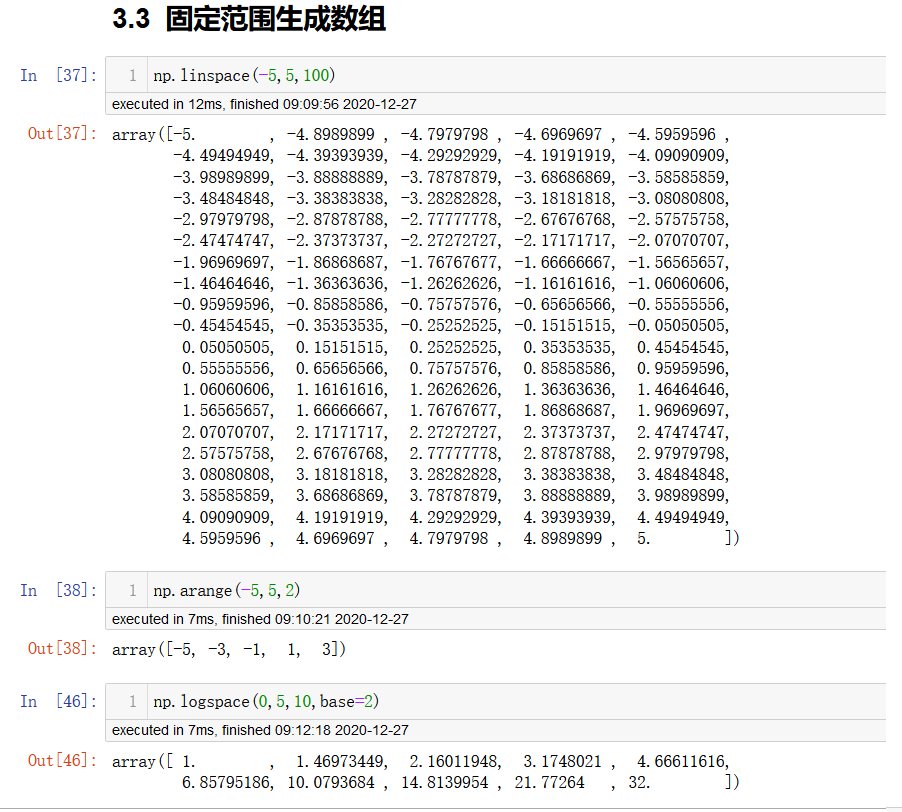
生成固定范围的数组

np.linspace(start,stop,num,endpoint)
# 在[start,stop],生成等间隔的num个数
# endpoint: 序列中是否包含stop值,默认为true]


np.arange(strat,stop,step,dtype)
# 类似range()

np.logspace(start,stop,num,base)
# 生成一个指数的序列
# 在[base**start,base**stop]生成等间隔的num个数

生成随机数组

使用模块

np.random模块

均匀分布

np.random.rand(d0,d1,d2..) 
# 返回[0.0,1,0)内的一组均匀分布的数
# d0,d1,d2... 是维度

np.random.uniform(low=0.0,high=1.0,size=None)
# 从一个均匀分布的[high,low)中随机采样

np.random.randint(low,high=None,size=None,dtype="I")
# 从一个均匀分布中随机采样,生成一个整数或N维整数数组
# 取数范围: 若high不为None,去[low,high),否则取[0,low)之间的随机整数.

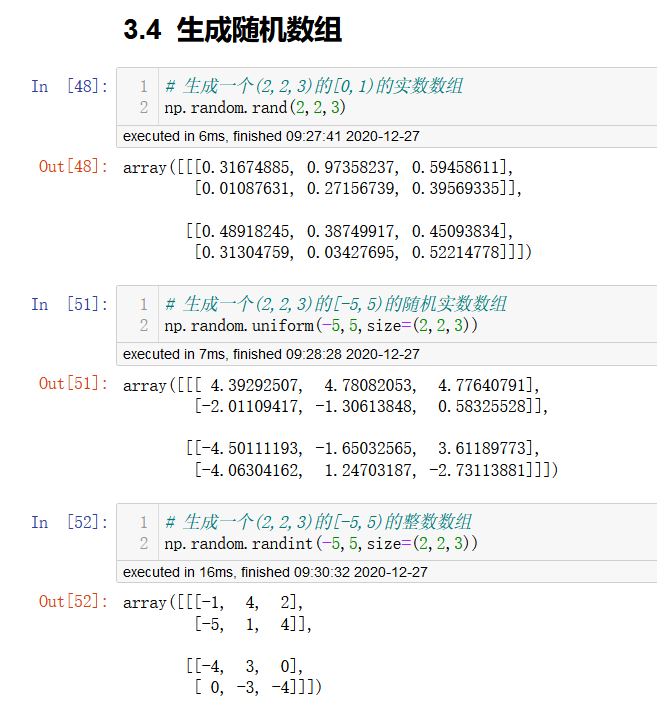
正态分布

什么是正态分布

正态分布是一种概率分布.
正态分布是具有两个参数μ和σ的连续性随机变量的分布, μ是随机变量的均值,σ是随机变量的标准差.

正态分布的应用

生活,生产与科学使验中很多随机变量的概率分布都可以近似地用正态分布来描述.

标准差与方差的意义

可以理解成数据的一个离散程度的衡量

正态分布的创建方式

np.random.randn(d0,d1,d2...)
# 从标准正态分布中返回一个或多个样本值

np.random.normal(loc=0.0,scale=1.0,size=None)
# 返回一个指定正态分布
# loc: 均值
# scale: 标准差

np.random.standard_normal(size=None)
# 返回一个指定形状的正态分布

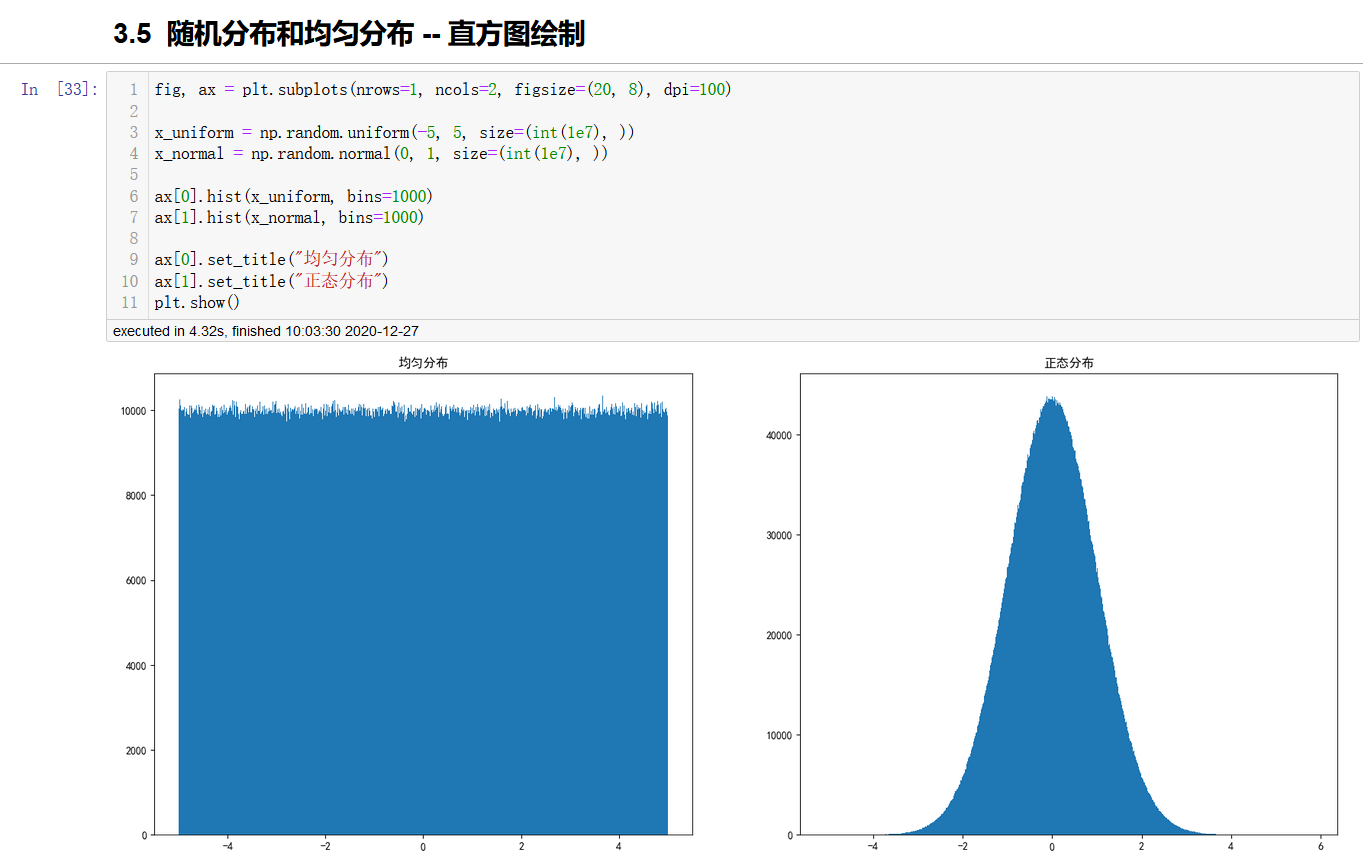
均匀分布和正态分布

通过绘制直方图来查看两者差别

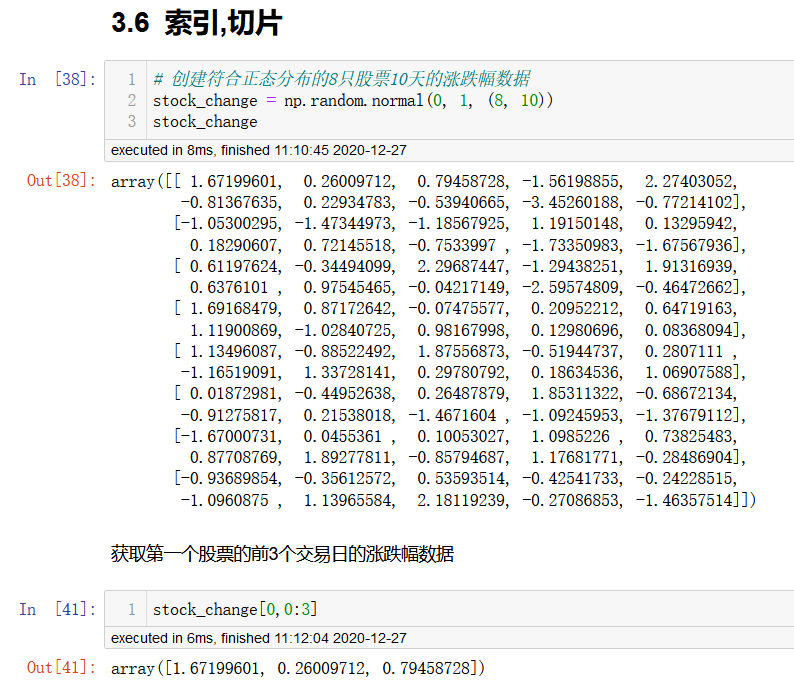
数组的索引,切片

我们可以模拟生成一组股票的涨跌幅的数据
案例：随机生成8只股票2周的交易日涨幅数据

8只股票，两周(10天)的涨跌幅数据，如何获取？
两周的交易日数量为：2 X 5 =10
随机生成涨跌幅在某个正态分布内，比如均值0，方差1

# 创建符合正态分布的8只股票10天的涨跌幅数据
stock_change = np.random.normal(0, 1, (8, 10))
stock_change

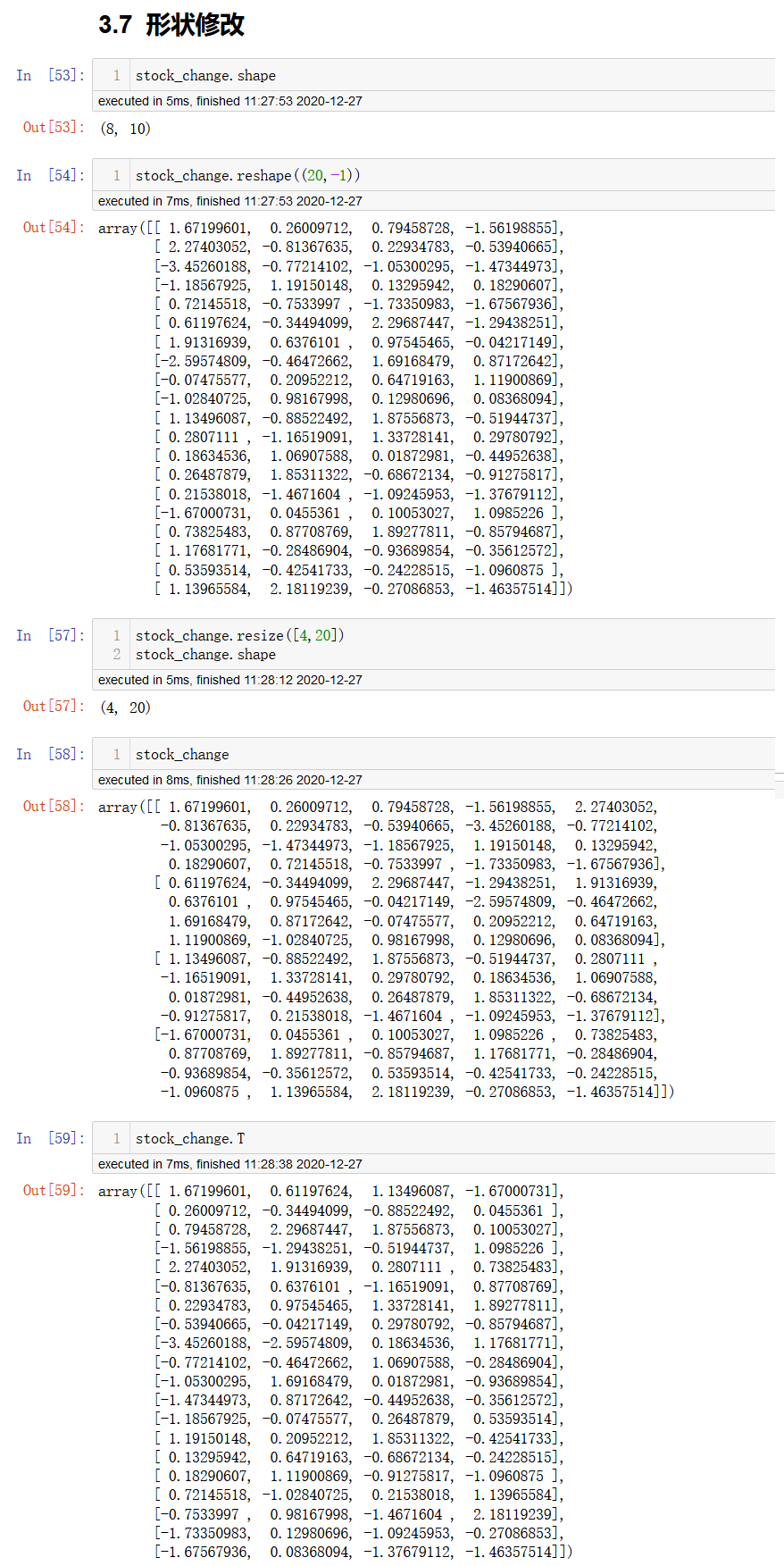
形状修改

ndarray.reshape(shape)
# 修改ndarray的形状,并返回一个新数组

ndarray.resize(shape)
# 在原数组上修改ndarray的形状

ndarray.T
# 转置

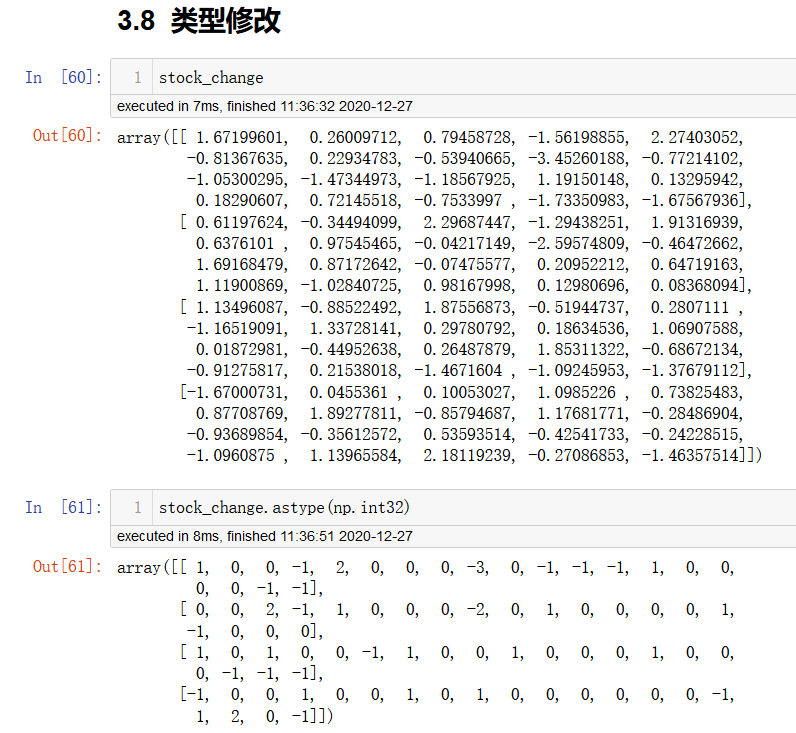
类型修改

ndarray.astype(类型)
# 修改数组的类型

数组去重

np.unique(ndarray)

ndarray运算

逻辑运算

ndarray 逻辑运算符 值
例: stock_change > 5
# 进行数组逻辑运算,返回一个布尔数组

ndarray[ndarray 逻辑运算符 值]
例: stock_change[stock_change > 5] = -10
# 对数组进行筛选,可以进行赋值的操作

通用判断函数

np.all(ndarray 逻辑运算符 值)
# 全部满足要求才返回True

np.any(ndarray 逻辑运算符 值)
# 任一满足要求就返回True

np.where(三元运算符)

通过使用np.where能够进行更加复杂的运算

np.where(数组逻辑表达式,值1,值2)
例: np.where(tmp>5,1,0)
# 判别式为真,则赋值为1,否则赋值为0

# 逻辑与,逻辑或
np.logical_and(条件1,条件2,...)
np.logical_or(条件1,条件2,...)

统计运算

统计指标

在数据挖掘/机器学习领域,统计指标的值也是我们分析问题的一种方式.
常用的指标如下:

np.min(a[, axis, out, keepdims])
    Return the minimum of an array or minimum along an axis.
np.max(a[, axis, out, keepdims])
    Return the maximum of an array or maximum along an axis.
np.median(a[, axis, out, overwrite_input, keepdims])
    Compute the median along the specified axis.
np.mean(a[, axis, dtype, out, keepdims])
    Compute the arithmetic mean along the specified axis.
np.std(a[, axis, dtype, out, ddof, keepdims])
    Compute the standard deviation along the specified axis.
np.var(a[, axis, dtype, out, ddof, keepdims])
    Compute the variance along the specified axis.

np.argmin(a[,axis]) 获取最小值索引
np.argmax(a[,axis]) 获取最大值索引   

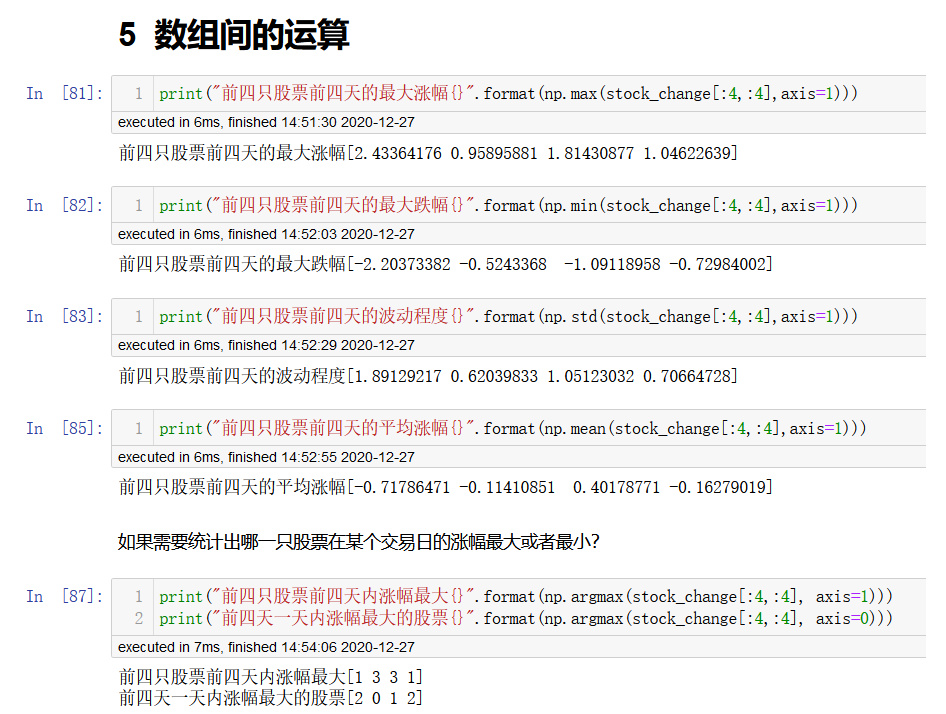
案例: 股票涨跌幅统计运算

在统计的时候,axis轴的取值并不一定,numpy中不同的api轴的值都不一样.
在这里,axis=0代表列,axis=1代表行.

数学: 矩阵

矩阵和向量

矩阵

矩阵matrix,和array的区别是矩阵必须是2维的,但array可以是多维的.

向量

向量是一种特殊的矩阵,讲义中的向量一般都是列向量.
下面展示三维列向量(3*1)

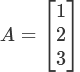
加法和标量乘法

矩阵向量乘法

下面是矩阵乘法必须满足的性质

矩阵乘法

矩阵乘法：
m×n 矩阵乘以 n×o 矩阵，变成 m×o 矩阵。
举例：比如说现在有两个矩阵 A 和 B，那 么它们的乘积就可以表示为图中所示的形式

下面是一个矩阵乘法的小练习

矩阵乘法的性质

逆,转置

矩阵的逆: 如矩阵A是一个m*m的矩阵(方阵),如果有逆矩阵,则:
\(AA^{-1} = A^{-1}A = I\)

矩阵转置就是\(A^T=B\),也就是矩阵的行列进行互换.

数组间的运算

场景

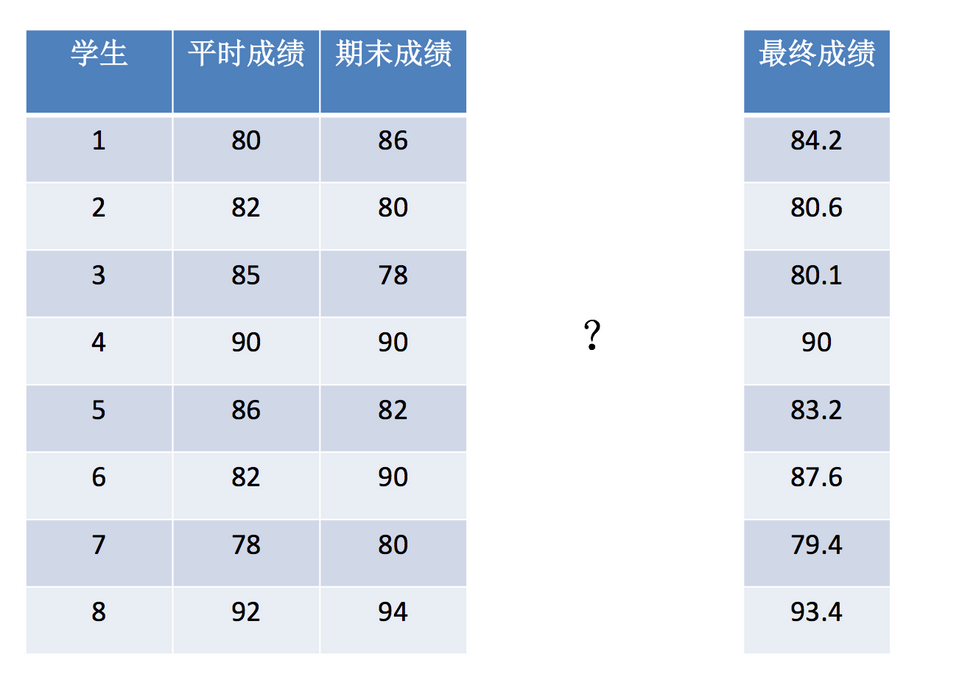
数据:

[[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]]

数组与数的运算

arr = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr + 1
arr / 2

# 可以对比python列表的运算，看出区别
a = [1, 2, 3, 4, 5]
a * 3

数组与数组的运算

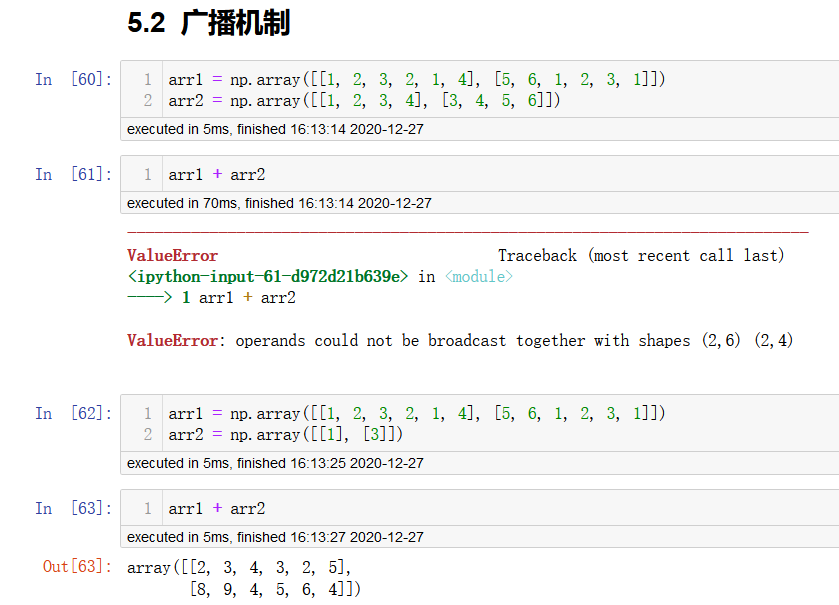
arr1 = np.array([[1, 2, 3, 2, 1, 4], [5, 6, 1, 2, 3, 1]])
arr2 = np.array([[1, 2, 3, 4], [3, 4, 5, 6]])

上面这个能进行运算吗，结果是不行的！

# 不符合广播机制,不能进行数组和数组的运算
arr1: 2,6
arr2: 2,4

广播机制

当操作两个数组时,numpy会逐个比较它们的shape(构成的元组tuple),只有在下述情况下,两个数组才能够进行数组与数组的运算.
(1) 维度相等
(2) 维度为1或没有

例如:

Image (3d array):  256 x 256 x 3
Scale (1d array):              3
Result (3d array): 256 x 256 x 3

A      (4d array):  9 x 1 x 7 x 1
B      (3d array):      8 x 1 x 5
Result (4d array):  9 x 8 x 7 x 5

A      (2d array):  5 x 4
B      (1d array):      1
Result (2d array):  5 x 4

A      (3d array):  15 x 3 x 5
B      (3d array):  15 x 1 x 1
Result (3d array):  15 x 3 x 5

如果是下面这样则不匹配

A  (1d array): 10
B  (1d array): 12
A  (2d array):      2 x 1
B  (3d array):  8 x 4 x 3

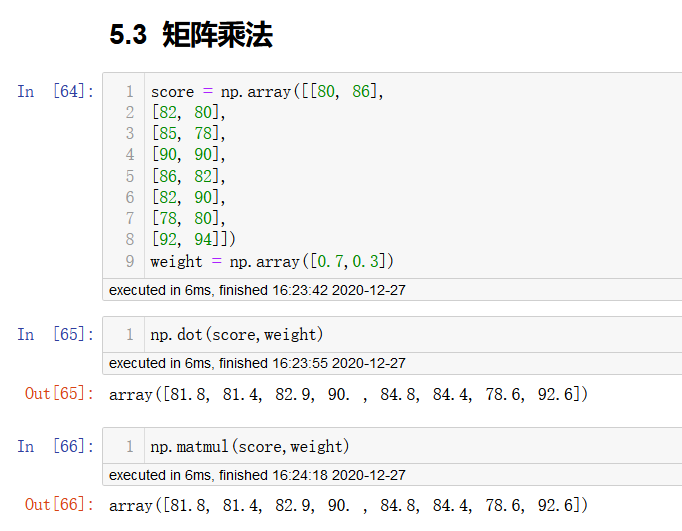
矩阵运算

np.dot(a,b) 
# 矩阵a和矩阵b点乘

np.matmul(a,b)
# 矩阵a和矩阵b进行矩阵乘法

np.matmul和np.dot的差别
二者都是矩阵乘法.
np.matmul中禁止矩阵和标量的成啊.
在矢量乘矢量的内积运算中,np.matmul和np.dot没有差别.