人工智能数学基础 | 高等数学基础 | 01
本章将介绍函数,极限,无穷大和无穷小,连续性与导数,偏导数,方向导数,梯度等高等数学基本概念.
这些概念贯穿本书的各个章节,也是理解人工智能算法的基础数学知识.
梯度下降算法是机器学习领域的重要算法,是应用最广泛的优化算法之一.
在本章综合实例中将重点介绍梯度下降法及其应用实例,并通过Python语言编程实现.
函数
我们经常会遇到彼此之间有依赖关系的变量,如圆的面积s=PI*r*r,我们称这种依赖关系为函数关系.
函数的定义

函数关系就是量和量之间的一种依赖关系.

x是自变量,y是因变量.
随着x的变换,y也会发生相应变化.
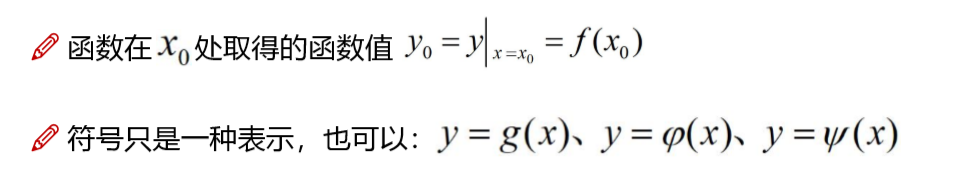
在函数当中我们有很多种写法,例如g(x),f(x)符号是什么并没有关系,它们表达的意义都是一样的, 都是表示变量和变量之间的一种关系.
几种特殊函数的定义
分段函数
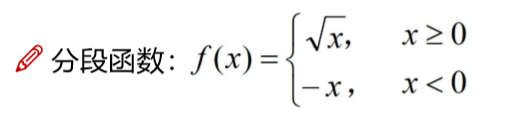
上面是最基本的一个分段函数,就是x取值不同时,会映射到不同的y值.
反函数
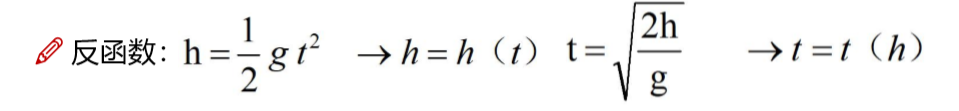
反函数就是把自变量和因变量交互了,比如上面自由落体公式h=h(t),其反函数可以写为t=t(h)
显函数与隐函数
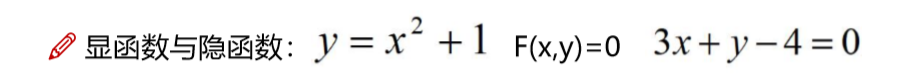
显函数和隐函数只是函数形式的一个概念.
显函数就是写好y=....的函数形式,就是把因变量放在左边.
隐函数就是写出来,比如x*x+1-y=0,a*a+b*b=16这些都是隐函数.
函数的几种特性
函数的奇偶性

奇函数关于原点对称,偶函数关于y轴对称.
函数的单调性
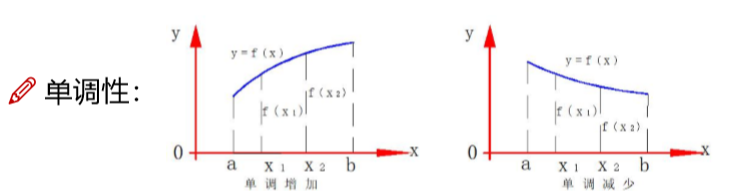
单调性很好理解,就看在一段区间内的函数值是否一直增加或一直减少.
函数的周期性
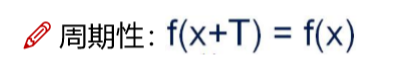
极限
极限概念是在探求某些实际问题的精确解答过程中产生的.
例如,第3章求解曲边梯形的面积就是采用划分无穷多个小梯形面积,然后求和得出曲边梯形的近似面积,这是极限思想在积分学中的应用.
第4章以泰勒多项式近似表达复杂函数,也是极限思想的应用.
极限方法是高等数学中的一种基本方法.
数列
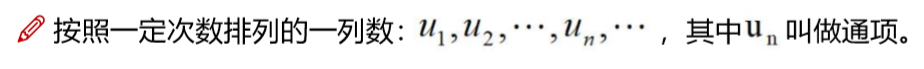
一堆数+排列=数列
其中Un表示通项,也就是其中的某一个数.

极限的符号表示

这里主要是∞和x0的极限表示.
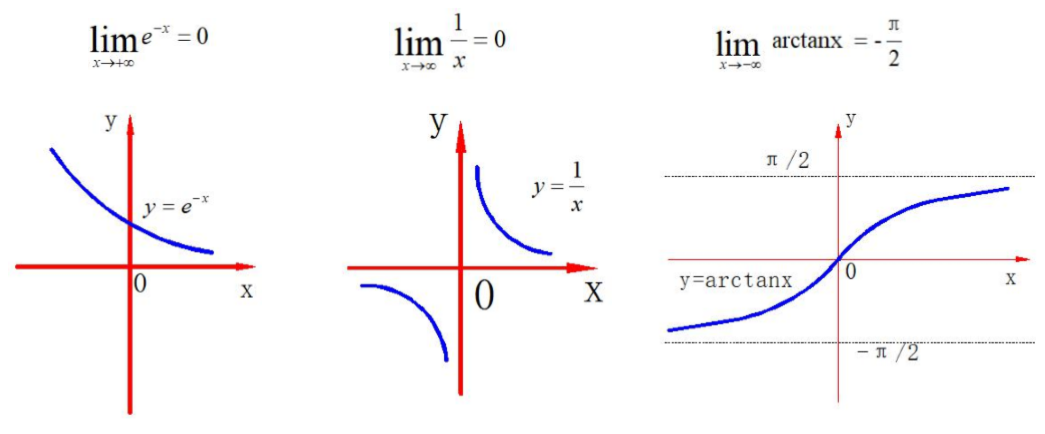
函数极限的定义
学习函数极限,主要研究一下两种情形.
(1) x->x0,对应f(x)的变换情形.
(2) x->∞,对应f(x)的变换情形.

下面是定义和反例

无穷大和无穷小
在极限当中经常会提到无穷小和无穷大,到底多小才是无穷小,多大才是无穷大呢?
下面我们给出定义及其性质.
无穷小
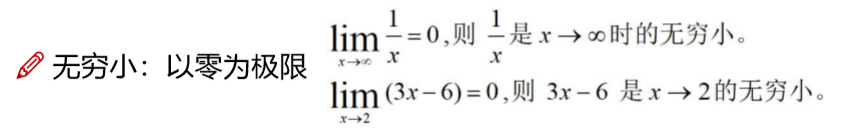
无穷小是0的极限.
该函数是x->值的无穷小.
无穷小的基本性质

无穷小和有边界(有限)和加法和乘法都是无穷小.
注意: 如果是无限的,那么无穷小运算的结果不一定是无穷小.(上图就给了一个反例)

注意: 无穷小的商不一定是无穷小.
无穷小于函数极限的关系
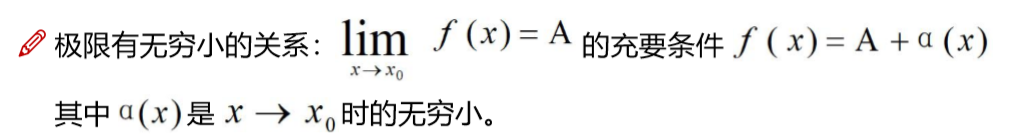
无穷小和函数极限的关系: x->x0,f(x)=A, 那么就会有 x->x0,f(x)=A+(x->x0是的一个无穷小)
无穷大

无穷大并不是一个非常大的数,而是相对一个过程来说的.
x->x0的时候,函数是一直增大的,没有一个收敛的点.
无穷大于无穷小的关系

如果f(x)为无穷大,则1/f(x)为无穷小,反之也成立.
无穷小的比较

(x->x0)有a和b两个无穷小,那么就需要比较这两个无穷小谁更"小".
进行(x->x0)a/b计算,
- 0,a是比b高阶的无穷小
- ∞,a是比b低阶的无穷小
- c(c≠0),a是b的同阶无穷小
- 1,a和b是等价无穷小
连续性和导数
函数建立了变量之间的依存关系,有时候也需要考虑函数的连续性.
例如气温的变化,当时间变动微小时,气温的变化也很微小,这种特点就是所谓连续性.
函数的连续性定义
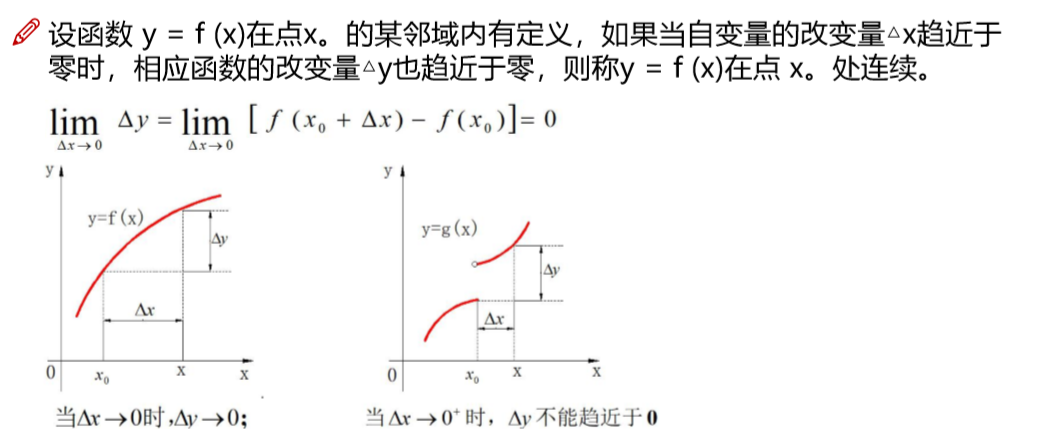
函数的连续性说白了就是x变化非常小(小到趋近于0),y的变化也是趋近于0的,就说这个函数是连续的.
否则,这种极限的思想会放大出这个"中断",比如上方的右图.
函数连续性需要满足的条件

函数f(x)在x0连续,需要满足上面三个条件.
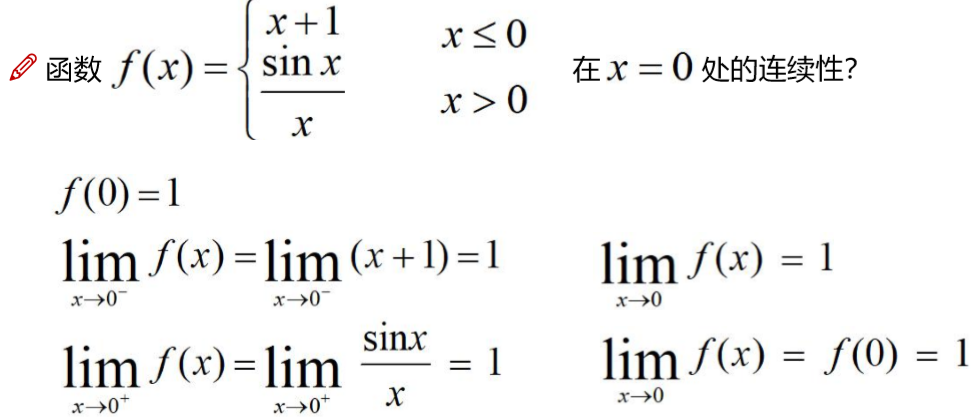
函数的间断点

如果f(x)在x0处不连续,这称x0为f(x)的间断点或不连续点.

f(x)在x0处是否连续要满足3个条件.
所以f(x)在x0处的间断点就有上面的几种情况.
函数间断点的常见类型

上面是间断点的类型,大致留个印象即可.

x=2,x=1没有定义,所有x=2,x=1为间断点.
然后再就是对间断点的细分.
导数
导数是一个非常重要的概念,本书很多章节都会用到此概念.
引列: 速度问题.
历史上速度问题于导数概念的形成有密切的关系.

导数的定义

导数本身的意义就是表达一种变化率.
函数的基本求导法则
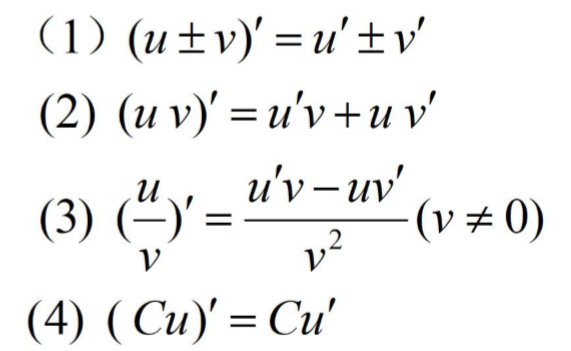
常用的求导公式
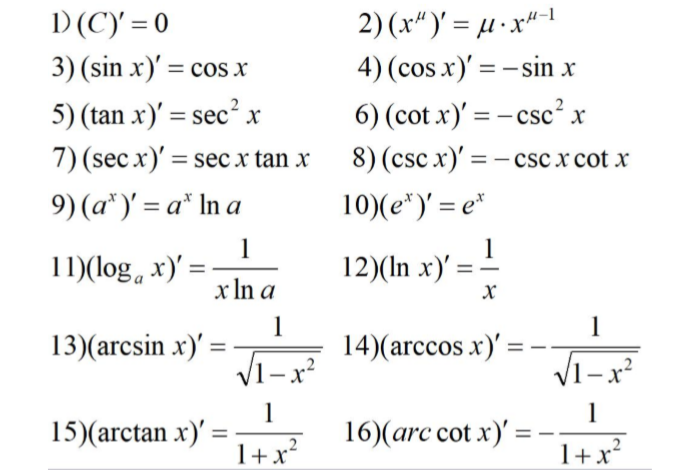
这些常用的求导公式不建议直接死记,建议还是使用到的时候在进行查阅.
偏导数
如果涉及的函数都只有一个自变量,那么这种函数被称为一元函数.
但在很多研究领域中,经常需要研究多个变量之间的关系,在数学上,这就表现为一个变量于另外多个变量的相互依赖关系.
二元函数就是函数值z随着两个自变量的变化而变化,记为z=f(x,y).
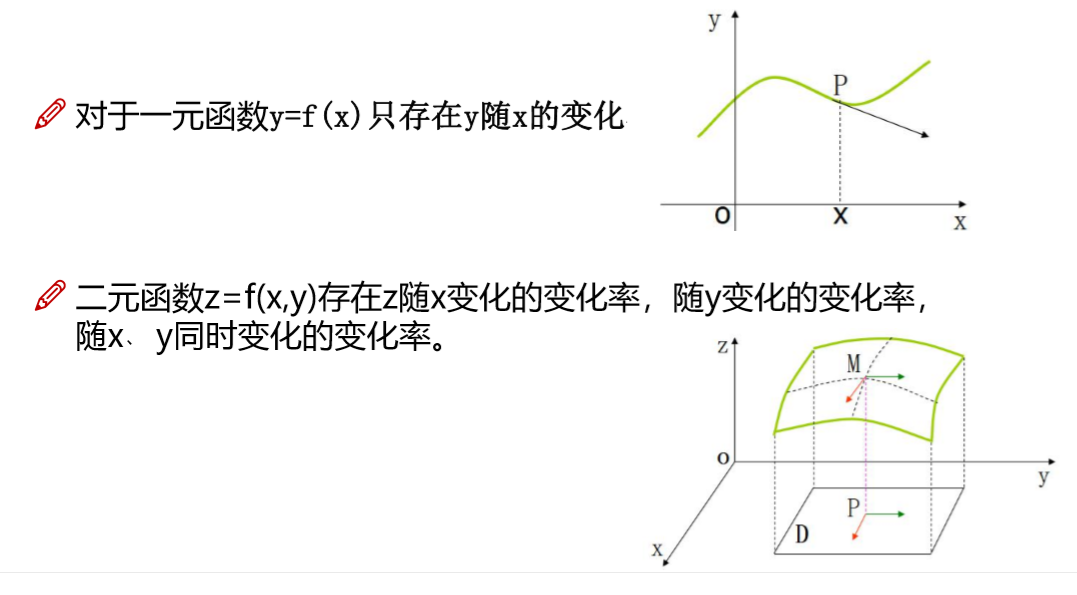
一元函数的导数反映了函数相对于自变量的变化率.
但多元函数的自变量有两个或两个以上,所以对于多元函数,在研究某个自变量的变化率时,往往把其他的自变量暂时固定下来,即视为常数,使其成为一元函数,然后再对其进行求导,这就是偏导数的概念.
偏导数的定义

偏导数的几何意义

如果是fx(x0,y0),那么就是 y=y0 和 曲面z=f(x,y)所截取出来的曲线Cx的斜率.
如果是fy(x0,y0),那么就是 x=x0 和 曲面z=f(x,y)所截取出来的曲线Cy的斜率.
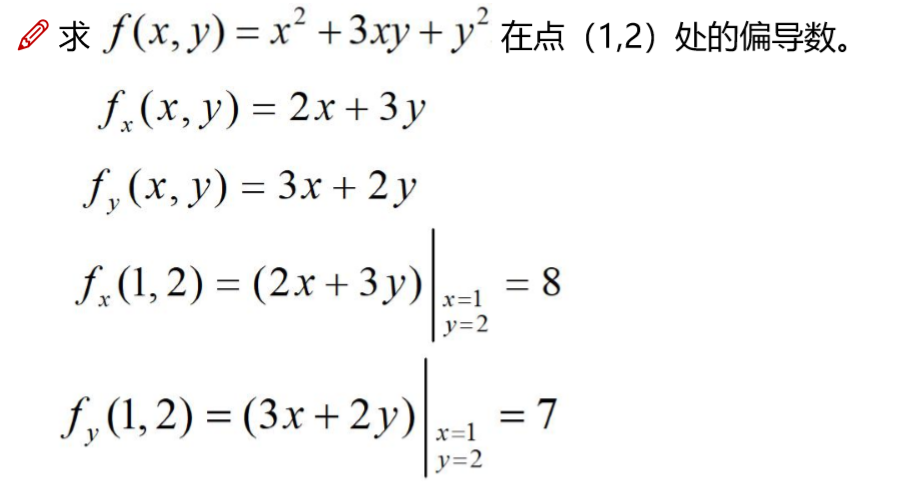
方向导数
偏导数反映的是函数沿坐标轴方向的变化率,方向导数本质上函数在某点处沿特定方向的变换率问题.
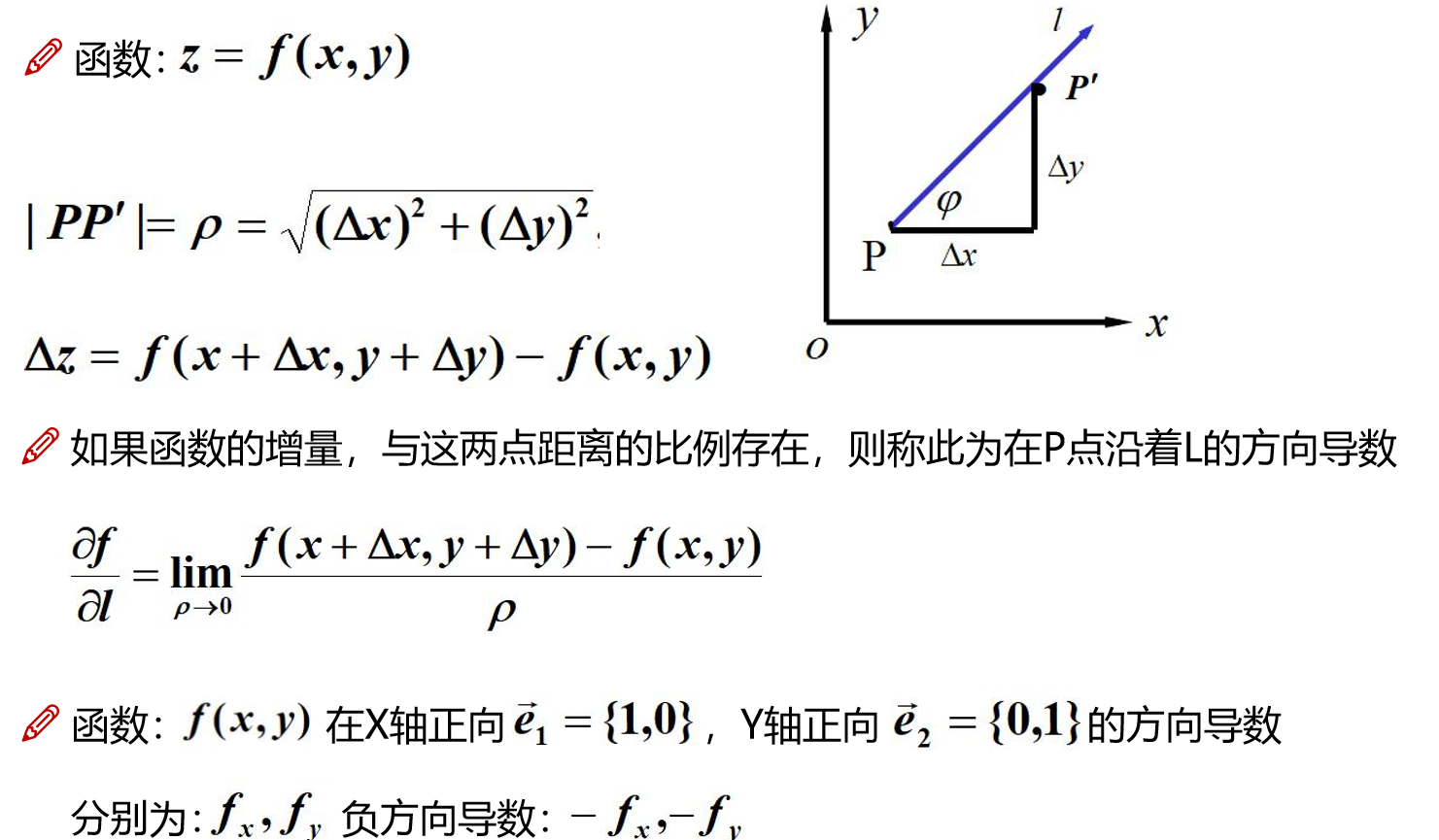
下面是有关于方向导数的定理
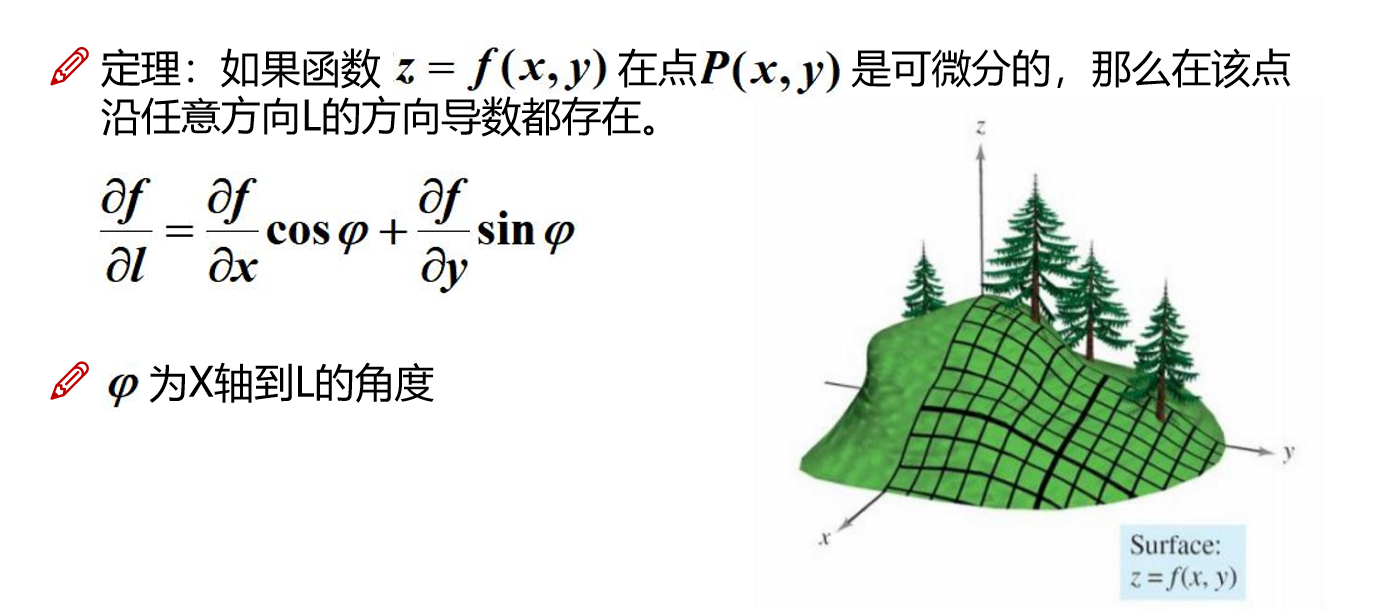

梯度
梯度就是一个关于方向导数的向量.

梯度的出现是为了求出方向导数的最大值和最小值.

理解梯度最好的例子就是: 着火蚂蚁逃生,下山最快的方向
综合案例: 梯度下降法求函数的最小值
梯度下降的基本原理:
假设曲面上一只蚂蚁如遇火灾,该如何快速逃跑呢?
此问题可以类比为一个下山的过程.
假设蚂蚁被困在高山上,需要快速找到山的最低点,即山谷,但此时山上的烟雾很大,可见度很低,下山的路径无法确定.
它必须利用自己周围的信息去寻找,这时候就可以利用梯度下降法来帮助自己下山.
以当前位置为准,寻找这个位置最陡峭的地方,朝着山的高度下降最快的地方走.
但是,由于山的地形复杂,坡度变化随机,这样一直往下走无法确定路径是否正确,因此可以采用每走一段路,就重新计算一次,最后就能成功抵达山谷.



 浙公网安备 33010602011771号
浙公网安备 33010602011771号