洛谷刷题杂记

• useful
  • \(\color{#E91}{普及-}\)
  • \(\color{#FC1}{普及/提高-}\)
  • \(\color{#6B1}{普及+/提高}\)
    • CF527D Clique Problem
  • \(\color{#48D}{提高+/省选-}\)
  • \(\color{#83C}{省选+/NOI-}\)
  • \(\color{#115}{NOI/NOI+/CTSC}\)
• 动态规划
  • \(\color{#E91}{普及-}\)
    • P1115 最大子段和
  • \(\color{#FC1}{普及/提高-}\)
    • P1140 相似基因
    • P1435 [IOI2000] 回文字串 / [蓝桥杯 2016 省] 密码脱落
    • P1775 石子合并（弱化版）
    • P2340 [USACO03FALL]Cow Exhibition G
  • \(\color{#6B1}{普及+/提高}\)
    • CF478D Red-Green Towers
    • CF505C Mr. Kitayuta, the Treasure Hunter
    • CF540D Bad Luck Island
    • CF607B Zuma
    • CF837D Round Subset
    • P1063 [NOIP2006 提高组] 能量项链
    • P1541 [NOIP2010 提高组] 乌龟棋
    • P1613 跑路
    • P1880 [NOI1995] 石子合并
    • P3146 [USACO16OPEN]248 G
    • P3147 [USACO16OPEN]262144 P (神奇的区间DP)
    • P3205 [HNOI2010]合唱队
    • P4170 [CQOI2007]涂色
    • P4290 [HAOI2008] 玩具取名
    • P4310 绝世好题 (带位运算)
    • P4316 绿豆蛙的归宿
  • \(\color{#48D}{提高+/省选-}\)
    • CF1265E Beautiful Mirrors
    • P1070 [NOIP2009 普及组] 道路游戏
    • P1220 关路灯
    • P1654 OSU!
    • P4342 [IOI1998]Polygon
    • P4550 收集邮票
  • \(\color{#83C}{省选+/NOI-}\)
    • P3232 [HNOI2013]游走
  • \(\color{#115}{NOI/NOI+/CTSC}\)
• 数据结构
  • \(\color{#E91}{普及-}\)
  • \(\color{#FC1}{普及/提高-}\)
    • P1774 最接近神的人
  • \(\color{#6B1}{普及+/提高}\)
    • CF547B Mike and Feet
    • P1253 [yLOI2018] 扶苏的问题
  • \(\color{#48D}{提高+/省选-}\)
    • P2163 [SHOI2007]园丁的烦恼
    • P4145 上帝造题的七分钟 2 / 花神游历各国
    • P4513 小白逛公园
    • P5522 [yLOI2019] 棠梨煎雪
    • P5677 [GZOI2017]配对统计
  • \(\color{#83C}{省选+/NOI-}\)
    • P1505 [国家集训队]旅游
    • P2572 [SCOI2010] 序列操作
    • P2633 Count on a tree
    • P3313 [SDOI2014]旅行
    • P3586 [POI2015] LOG
    • P4592 [TJOI2018]异或
    • P4735 最大异或和
    • P5283 [十二省联考 2019] 异或粽子
  • \(\color{#115}{NOI/NOI+/CTSC}\)
• 字符串
  • \(\color{#E91}{普及-}\)
  • \(\color{#FC1}{普及/提高-}\)
    • P1481 魔族密码
  • \(\color{#6B1}{普及+/提高}\)
  • \(\color{#48D}{提高+/省选-}\)
    • P1368 【模板】最小表示法
    • P1659 [国家集训队]拉拉队排练
    • P2870 [USACO007DEC]Best Cow Line G
    • P2922 [USACO08DEC]Secret Message G
    • P3501 [POI2010]ANT-Antisymmetry
    • P4287 [SHOI2011]双倍回文
    • P4555 [国家集训队]最长双回文串
  • \(\color{#83C}{省选+/NOI-}\)
    • P2408 不同子串个数
    • P2852 [USACO06DEC]Milk Patterns G
    • P4051 加密字符
    • P5410 【模板】扩展 KMP（Z 函数）
  • \(\color{#115}{NOI/NOI+/CTSC}\)
• 图论, 搜索
  • \(\color{#E91}{普及-}\)
  • \(\color{#FC1}{普及/提高-}\)
  • \(\color{#6B1}{普及+/提高}\)
    • CF796D Police Stations
  • \(\color{#48D}{提高+/省选-}\)
  • \(\color{#83C}{省选+/NOI-}\)
  • \(\color{#115}{NOI/NOI+/CTSC}\)
• 数学
  • \(\color{#E91}{普及-}\)
  • \(\color{#FC1}{普及/提高-}\)
  • \(\color{#6B1}{普及+/提高}\)
    • P5104 红包发红包
  • \(\color{#48D}{提高+/省选-}\)
  • \(\color{#83C}{省选+/NOI-}\)
  • \(\color{#115}{NOI/NOI+/CTSC}\)
• 奇怪的题目
  • \(\color{#E91}{普及-}\)
  • \(\color{#FC1}{普及/提高-}\)
  • \(\color{#6B1}{普及+/提高}\)
  • \(\color{#48D}{提高+/省选-}\)
  • \(\color{#83C}{省选+/NOI-}\)
  • \(\color{#115}{NOI/NOI+/CTSC}\)

useful

\(\color{#E91}{普及-}\)

\(\color{#FC1}{普及/提高-}\)

\(\color{#6B1}{普及+/提高}\)

CF527D Clique Problem

推式子转化为 最大不相交区间数量 的贪心模型

题意

数轴上有 \(n\) 个点，第 \(i\) 个点的坐标为 \(x_i\) ，权值为 \(w_i\) 。两个点 \(i,j\) 之间存在一条边当且仅当
\(abs(x_i − x_j )\geq w_i +w_j\) 。 你需要求出这张图的最大团的点数。

团的定义：两两之间有边的顶点集合。

数据范围
\(1\leq n \leq 2 * 10^5\)
\(1\leq x_i, w_i \leq 10^9\)

思路

• 很容易推出当 \(x_i-w_i \geq x_j + w_j\) 时, 两个点能连边
• 转化: \(l[i]=x_i-w_i, r[i] = x_j + w_j\), 则题意就是求最大不相交的区间数量

Solution

#include<bits/stdc++.h>
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
vector<int> v;

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	vector<PII> a(n);
	for(int i = 0; i < n; i++){
		int x, w;
		cin >> x >> w;
		a[i].x = x - w, a[i].y = x + w;
	}
	sort(arr(a));
	int ans = 0, ed = -1e9;
	for(int i = 0; i < n; i++){
		if(a[i].x >= ed) ans ++, ed = a[i].y;
		else ed = min(a[i].y, ed);
	}
	cout << ans << endl;
    return 0;
}

\(\color{#48D}{提高+/省选-}\)

\(\color{#83C}{省选+/NOI-}\)

\(\color{#115}{NOI/NOI+/CTSC}\)

动态规划

\(\color{#E91}{普及-}\)

P1115 最大子段和

水, 最基础线性DP

传送门

Solution

#include<bits/stdc++.h>
typedef long long ll;
#define endl "\n"
using namespace std;
const int N = 2e5 + 10;
int f[N];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	vector<int> a(n + 1, 0);
	for(int i = 1; i <= n; i++)
		cin >> a[i];
	for(int i = 1; i <= n; i++){
		f[i] = max(a[i], f[i - 1] + a[i]);
	}
	int mx = -2e9;
	for(int i = 1; i <= n; i++)
		mx = max(mx, f[i]);
	cout << mx << endl;
    return 0;
}

\(\color{#FC1}{普及/提高-}\)

P1140 相似基因

典中典双序列匹配问题, 可能书中放在区间DP感觉怪怪的

传送门

思路

• 就按照最长公共子序列的状态定义方式就好了
• 然后很容易的就能写出状态转移方程了

Solution

#include<bits/stdc++.h>
typedef long long ll;
#define endl "\n"
using namespace std;
const int N = 110;
unordered_map<char, int> mp;
int d[6][6], f[N][N];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	mp['A'] = 1, mp['C'] = 2, mp['G'] = 3, mp['T'] = 4;
	d[1][1] = 5, d[1][2] = -1, d[1][3] = -2, d[1][4] = -1, d[1][5] = -3,
	d[2][1] = -1, d[2][2] = 5, d[2][3] = -3, d[2][4] = -2, d[2][5] = -4,
	d[3][1] = -2, d[3][2] = -3, d[3][3] = 5, d[3][4] = -2, d[3][5] = -2,
	d[4][1] = -1, d[4][2] = -2, d[4][3] = -2, d[4][4] = 5, d[4][5] = -1,
	d[5][1] = -3, d[5][2] = -4, d[5][3] = -2, d[5][4] = -1; 
	int n, m;
	string s1, s2;
	cin >> n >> s1 >> m >> s2;
	s1 = " " + s1;
	s2 = " " + s2;
	for(int i = 0; i <= n; i++){
		for(int j = 0; j <= m; j++){
			if(!i && !j){
				f[i][j] = 0;
				continue;
			}
			if(i && j)
				f[i][j] = max({f[i - 1][j - 1] + d[mp[s1[i]]][mp[s2[j]]], f[i - 1][j] + d[mp[s1[i]]][5], f[i][j - 1] + d[5][mp[s2[j]]]});
			if(!i)
				f[i][j] = f[i][j - 1] + d[5][mp[s2[j]]];
			if(!j)
				f[i][j] = f[i - 1][j] + d[mp[s1[i]]][5];
		}
	}
	cout << f[n][m] << endl;
    return 0;
}

P1435 [IOI2000] 回文字串 / [蓝桥杯 2016 省] 密码脱落

两种解法, 一个区间DP, 一个做反串后求两串LCS

题意

回文词是一种对称的字符串。任意给定一个字符串，通过插入若干字符，都可以变成回文词。此题的任务是，求出将给定字符串变成回文词所需要插入的最少字符数。

比如 “Ab3bd”插入2个字符后可以变成回文词“dAb3bAd”或“Adb3bdA”，但是插入少于2个的字符无法变成回文词。

注：此问题区分大小写

数据范围
\(0\leq |s| \leq 1000\)

思路

• 线性dp很难搞, 考虑区间DP
• 状态: \(f[i][j]\) 表示子区间 \([i,j]\) 变成回文串最小次数
• 转移: f[l][r] = min(f[l+1][r],f[l][r-1]) + 1, if(s[l] == s[r]) f[l][r] = min(f[l][r], f[l + 1][r - 1])

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
int f[1010][1010];
// f[l][r] 表示 将区间[l,r] 变成回文串的最小次数，然后有类似有 LCS 那样的状态转移
int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	string s;
	cin >> s;
	int n;
	n = s.size();
	s = " " + s;
	for(int len = 1; len <= n; len ++){
		for(int l = 1; l + len - 1 <= n; l++){
			int r = l + len - 1;
			f[l][r] = min(f[l + 1][r], f[l][r - 1]) + 1;
			if(s[l] == s[r]){
				f[l][r] = min(f[l][r], f[l + 1][r - 1]);
			}
		}
	}
	cout << f[1][n] << endl;
    return 0;
}

P1775 石子合并（弱化版）

区间DP 模板题

传送门

#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
const int N = 310;
int f[N][N];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	vector<int> a(n + 1, 0);
	for(int i = 1; i <= n; i++)
		cin >> a[i];
	for(int i = 1; i <= n; i++)
		a[i] = a[i - 1] + a[i];
	memset(f, 0x3f, sizeof f);
	for(int len = 1; len <= n; len ++){
		for(int l = 1; l + len - 1 <= n; l++){
			int r = l + len - 1;
			if(len == 1){
				f[l][r] = 0;
				continue;
			}
			for(int k = l; k < r; ++)
				f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + a[r] - a[l - 1]);
		}
	}
	cout << f[1][n] << endl;
    return 0;
}k

P2340 [USACO03FALL]Cow Exhibition G

有趣的寻找答案方式, 背包体积为负数, 滚动数组正序枚举

题意

奶牛想证明它们是聪明而风趣的。为此，贝西筹备了一个奶牛博览会，她已经对 \(N\) 头奶牛进行了面试，确定了每头奶牛的智商 \(S_i\) 和情商 \(F_i\)。

贝西有权选择让哪些奶牛参加展览。由于负的智商或情商会造成负面效果，所以贝西不希望出展奶牛的智商之和小于零，或情商之和小于零。满足这两个条件下，她希望出展奶牛的智商与情商之和越大越好，请帮助贝西求出这个最大值。

数据范围
\(-1000\leq S_i,F_i\leq 1000\)
\(n\leq400\)

思路

• 毫无疑问考虑01背包求解, 如何表示状态
• f[i][?], 阶段很明确选到第 i 头牛, 第二维直接采用 情商加智商和 实际上不好解决问题.
• 考虑将两个限制变为一个限制, 即 \(f[i][j]\) 表示到第 i 头牛, 情商/智商为 j 的智商/情商和最大值, 那么最后遍历一遍 max(f[n][j] + j) 即可
• 细节: 智商存在负数, 智商和平移, 并且背包体积有负数时, 滚动数组需要正序枚举.

Solution

#include<bits/stdc++.h>
#define s first
#define f second
#define endl "\n"
using namespace std;
const int N = 8e5;
int f[N + 10], n;
PII cow[410];
// 目标答案并不一定使用一个维度就能表示出来，A + B 的最大和， 可以记录 A 的最大值， 最后遍历状态值 + B 找到 A+B 最大值
int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n;
	for(int i = 1; i <= n; i++)
		cin >> cow[i].s >> cow[i].f;
	memset(f, -0x3f, sizeof f);
	f[N / 2] = 0;
	for(int i = 1; i <= n; i++){
		if(cow[i].s >= 0)
			for(int j = N; j >= cow[i].s; j--){
					f[j] = max(f[j - cow[i].s] + cow[i].f , f[j]);
			}
		else
			for(int j = 0; j <= N + cow[i].s; j++)		// 体积为负，需要正序枚举，注意背包大小
					f[j] = max(f[j], f[j - cow[i].s] + cow[i].f);
	}
	int ans = 0;
	for(int i = N / 2; i <= N; i++){
		if(f[i] >= 0)
			ans = max(ans, f[i] + i - N / 2);
	}
	cout << ans << endl;
    return 0;
}

\(\color{#6B1}{普及+/提高}\)

CF478D Red-Green Towers

01背包, 状态变形, 滚动数组

题意

你有r块红色的积木和g块绿色的积木，它们用于建造红绿塔。红绿塔按照下面的规则来建造：
红绿塔有若干层；
如果红绿塔有 \(n\) 层，那么塔的第一层应该有 \(n\) 块积木，第二层有 \(n-1\) 块，第三层有 \(n-2\) 块，以此类推，最后一层只有一块。换言之，每一层应该比前面一层少一块；
红绿塔的每一层必须使用相同颜色的积木。
设h是红绿塔的目标层数，它由 \(r\) 块红色积木和 \(g\) 快绿色积木组成，并且满足上述规则。现在你的任务是确定可以建造出多少不同的有 \(h\) 层的红绿塔。

如果两个红绿塔相同的一层使用的是不同的颜色，它们就被认为不同的。

你需要写一个程序来求出有多少种高度为 \(h\) 的不同的红绿塔。由于答案很大，你只需要输出答案模 \(10^9+7\) 后的值。

数据范围
\(0 \leq r,g \leq 2 * 10^5\)

思路

• 一开始没想通怎么确定高度, 首先个数为 \(tot = h*(h+2) / 2\) , 如果 \(tot > r + g\) 显然不成立, 所以 \(tot \leq r + g\).
• 那么就会有方块多或者少, 其实并不影响答案统计, 判断一下边界好像就可以了
• 状态: \(f[i][j]\) 表示到第 i 层, 红色砖块用了 j 个的方案数
• 转移很简单, 最后的答案要在合法的砖块使用范围内, 以后能写的话不要犹豫, 先冲个状态转移试试...

Solution

#include<bits/stdc++.h>
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
const int N = 2e5 + 10, mod = 1e9 + 7;
int f[N];

void add(int &a, int b){
	a = (a + b) % mod;
}

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int r, g, h = 0;
	cin >> r >> g;
	while((h) * (h + 1) / 2 <= r + g) h++;
	h--;
	f[0] = 1;
	for(int i = h; i >= 1; i--)
		for(int j = r; j >= i; j--)
			add(f[j], f[j - i]);
	int ans = 0;
	for(int i = r; i >= max(h * (h + 1) / 2 - g, 0); i--)
		add(ans, f[i]);
	cout << ans << endl;
    return 0;
}

CF505C Mr. Kitayuta, the Treasure Hunter

线性DP变形, 优化时空的另一种思路, 类似势能线段树的想法

题意

在一个有\(n\) 个点的岛屿上，有 \(n\) 个点有宝藏。现在给你一个 \(d\)。

开始你在 \(0\) 第一步，你将跳到 \(d\) 处之后你可以选择跳 $c-1,c,c+1 $ 步( \(c\) 为你上一步跳的步数)

每跳到某处可获得该地宝藏, 询问最大宝藏数

数据范围
\(1\leq n,d \leq 30000\)
\(1\leq p_i, \leq 30000\)

思路

• 直接存当前步数和位置显然不行
• 观察数据范围, 贪心的想每次增加一步, 最多增加 \(200\) 多次就到达了终点, 等差数列求和大概是 \(30000^{\frac{1}{2}}\) 级别.
• 所以我们直接拿相对 \(d\) 的变化大小作为维度, 这样也可以从上一个位置状态转移到现在位置
• 状态: \(f[i][j]\) 表示当前处在 \(i\) 位置, 上一步变化了 \(j\) 步大小.
• 转移: 见代码, 细节处理变化为负数, 平移数组即可

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
const int N = 3e4, D = 300;
int f[N + 10][D * 2 + 10], val[N + 10];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n, d;
	cin >> n >> d;
	for(int i = 0; i < n; i++){
		int x;
		cin >> x;
		val[x] ++;
	}
	memset(f, -0x3f, sizeof f);
	f[d][D] = val[0] + val[d];
	int ans = f[d][D];
	for(int i = d; i <= N; i++){
		for(int delta = -D; delta <= D; delta++){
			int j = delta + D;
			if(f[i][j] == -0x3f3f3f3f) continue;
			for(intk = -1; k <= 1; k++){
				int len = d + delta + k;
				if(i + len > N || len < 1 || delta + k < -D || delta + k > D) continue;
				f[i + len][j + k] = max(f[i + len][j + k], f[i][j] + val[i + len]);
				ans = max(ans, f[i + len][j + k]);
			}
		}
	}
	cout << ans << endl;
    return 0;
} 

CF540D Bad Luck Island

简单概率DP, 正推即可, 非常符合我的水平

题意

给三种人，分别是r,s,p个；

在孤岛上，每两个不同种人相遇则互吃,r吃s,s吃p,p吃r

求最后留下单一种族的概率

思路

• 对于求概率, 正推状态转移
• 状态: \(f[i][j][k]\) 分别表示三种人剩余情况
• 转移: \(f[i - 1][j][k] += \frac{i * k}{i*k+i*j+j*k}\) , 其他情况类比即可

#include<bits/stdc++.h>
typedef long long ll;
#define endl "\n"
using namespace std;
const int N = 105;
double f[N][N][N];	

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int r, s, p;
	cin >> r >> s >> p;
	f[r][s][p] = 1;
	for(int i = r; i >= 0; i--){
		for(int j = s; j >= 0; j--){
			for(int k = p; k >= 0; k--){
				if((i == 0) + (j == 0) + (k == 0) >= 2)
					continue;
				int tot = i + j + k;
				double down = (i * j + j * k + i * k);
				if(i)
					f[i - 1][j][k] += f[i][j][k] * (i * k) / down;
				if(j)
					f[i][j - 1][k] += f[i][j][k] * (i * j) / down;
				if(k)
					f[i][j][k - 1] += f[i][j][k] * (j * k) / down;
			}
		}
	}
	double an1 = 0, ans2 = 0, ans3 = 0;
	for(int i = 1; i <= r; i++){
		ans1 += f[i][0][0];
	}
	for(int i = 1; i <= s; i++)
		ans2 += f[0][i][0];
	for(int i = 1; i <= p; i++)
		ans3 += f[0][0][i];
	cout << fixed << setprecision(9) << ans1 << " " << ans2 << " " << ans3 << endl;
    return 0;
}s

CF607B Zuma

经典区间DP, 左右端点相同, 如果内部是回文串, 转移是没有代价的, 处理一下边界

传送门

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
const int N = 510;
int f[N][N];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	vector<int> a(n + 1, 0);
	for(int i = 1; i <= n; i++)
		cin >> a[i];
	memset(f, 0x3f, sizeof f);

	for(int len = 1; len <= n; len++){
		for(int l = 1; l + len - 1 <= n; l++){
			int r = l + len - 1;
			if(a[l] == a[r]){
				f[l][r] = (len <= 2) ? 1 : min(f[l][r], f[l + 1][r - 1]);
			}
			for(int k = l; k < r; k++)
				f[l][r] = mn(f[l][r], f[l][k] + f[k + 1][r]);
		}
	}
	cout << f[1][n] << endl;
    return 0;
}i

CF837D Round Subset

对于需要同时满足两个目标价值的背包, 可以将一个目标价值转化为状态维度

题意

给定 \(n\) 个整数 \(a_1,a_2,...,a_n\)。

请你从中选取恰好 \(k\) 个数，要求选出的数的乘积的末尾 \(0\) 的数量尽可能多。

请输出末尾 \(0\) 的最大可能数量。

思路

• 见代码

数据范围
\(1\leq n\leq 200\)
\(1\leq a_i \leq 10^18\)

Solution

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 210, M = 5010;
typedef long long ll;
int v[N], w[N];     // 10^t = 5^t * 2^t;
int f[N][M];        // f[i][j] 表示恰好选i个物品，有j个5最多有多少个2。     1e18 内因子最多有25个5， 25*200 = 5000;
                    // 省去了在前多少个物品选这一维
int n, m;

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i++){
        ll x;
        cin >> x;
        while(x % 5 == 0) x /= 5, v[i] ++;
        while(x % 2 == 0) x /= 2, w[i] ++;
    }
    memset(f, -0x3f, sizeof f);
    f[0][0] = 0;
    for(int i = 1; i <= n; i++){
        for(int j = m; j ; j--){
            for(int k = M; k >= v[i]; k--)
                f[j][k] = max(f[j][k], f[j - 1][k - v[i]] + w[i]);
        }
    }
    int res = 0;
    for(int i = 0; i < M; i++)
        res = max(res, min(i, f[m][i]));
    cout << res << endl;
    
    
    return 0;
}

P1063 [NOIP2006 提高组] 能量项链

环形区间DP, 石子合并变形

传送门

Solution

#include<bits/stdc++.h>
typedef long long ll;
#define endl "\n"
using namespace std;
const int N = 110;
int f[N << 1][N << 1];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	vector<int> head(2 * n + 1, 0);
	vector<int> tail(2 * n + 1, 0);
	for(int i = 1; i <= n; i++)
		cin >> head[i];
	for(int i = 1; i <= n; i++){
		if(i != n)
			tail[i] = head[i + 1];
		else
			tail[i] = head[1];
	}
	for(int i = 1; i <= n; i++)
		head[i + n] = head[i], tail[i + n] = tail[i];
	for(int len = 2; len <= n; len++){
		for(int l = 1; l + len - 1 <= 2 * n; l ++){
			int r = l + len - 1;
			for(int k = l; k < r; k++){
				f[l][r] = max(f[l][r], f[l][k] + f[k + 1][r] + head[l] * tail[k] * tail[r]);
			}
		}
	}
	int ans = 0;
	for(int i = 1; i <= n; i++)
		ans = max(ans, f[i][i + n - 1]);
	cout << ans << endl;
    return 0;
}

P1541 [NOIP2010 提高组] 乌龟棋

很有意思的状态表示与转移

题意

乌龟棋的棋盘是一行 \(N\) 个格子，每个格子上一个分数（非负整数）。棋盘第1格是唯一的起点，第 \(N\) 格是终点，游戏要求玩家控制一个乌龟棋子从起点出发走到终点。

乌龟棋中 \(M\) 张爬行卡片，分成4种不同的类型（\(M\) 张卡片中不一定包含所有
4种类型的卡片，见样例），每种类型的卡片上分别标有1,2,3,4四个数字之一，表示使用这种卡片后，乌龟棋子将向前爬行相应的格子数。游戏中，玩家每次需要从所有的爬行卡片中选择一张之前没有使用过的爬行卡片，控制乌龟棋子前进相应的格子数，每张卡片只能使用一次。

游戏中，乌龟棋子自动获得起点格子的分数，并且在后续的爬行中每到达一个格子，就得到该格子相应的分数。玩家最终游戏得分就是乌龟棋子从起点到终点过程中到过的所有格子的分数总和。

很明显，用不同的爬行卡片使用顺序会使得最终游戏的得分不同，小明想要找到一种卡片使用顺序使得最终游戏得分最多。

现在，告诉你棋盘上每个格子的分数和所有的爬行卡片，你能告诉小明，他最多能得到多少分吗？

数据范围
\(1\leq N \leq 350\)
\(1\leq M \leq 120\)
\(每种卡片最多40个\)

思路

• 重点在于状态的表示: f[i][j][k][l] 表示已经消耗了 i, j, k, l 张1,2,3,4数字的卡片的最大得分.
• 值得一提的是, 此题没有明显的阶段标志, 重点在状态转移, 循环顺序上, 符合 dp 要求.
• f[0][0][0][0] = a[1] 起点状态, 状态转移 f[i][j][k][l] = max(f[i][j][k][l], f[i - 1][j][k][l], f[i][j - 1][k][l], f[i][j][k - 1][l], f[i][j][k][l - 1] + a[1 + i+2*j+3*k+4*l])

Solution

#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
int f[41][41][41][41];		// f[i][j][k][l] 表示 消耗i张1，j张2，k张3，l张4, 最大积分

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n, m;
	cin >> n >> m;
	vector<int> a(n + 1, 0);
	vector<int> b(4, 0);
	for(int i = 1; i <= n; i++)
		cin >> a[i];
	for(int i = 0; i < m; i++){
		int x;
		cin >> x;
		b[x - 1] ++;
	}
	f[0][0][0][0] = a[1];		// 初始在 a[1] 位置
	for(int i = 0; i <= b[0]; i++)
		for(int j = 0; j <= b[1]; j++)
			for(int k = 0; k <= b[2]; k++)
				for(int l = 0; l <= b[3]; l++){
					int idx = 1 + i + 2 * j + 3 * k + 4 * l;	// 最终位置等于跳跃距离 + 1（起点）
					if(idx > n) continue;
					if(i)
						f[i][j][k][l] = max(f[i][j][k][l], f[i - 1][j][k][l] + a[idx]);
					if(j)
						f[i][j][k][l] = max(f[i][j][k][l], f[i][j - 1][k][l] + a[idx]);
					if(k)
						f[i][j][k][l] = max(f[i][j][k][l], f[i][j][k - 1][l] + a[idx]);
					if(l)
						f[i][j][k][l] = max(f[i][j][k][l], f[i][j][k][l - 1] + a[idx]);
				}
	cout << f[b[0]][b[1]][b[2]][b[3]] << endl;
    return 0;
}

P1613 跑路

图上DP, 倍增思想预处理, 做出最短路

题意

有 \(n\) 点 \(m\) 边的有向图, 每条边长度为 \(1\), 若一条路径长度是 \(2\) 的幂次, 则可以 1 秒跑完, 求从 \(1\) 到 \(n\) 的最少时间

数据范围
\(1\leq n \leq 50\)
\(1\leq m \leq 10000\)

思路

• 由于一条路径是 \(2^k\) 可以一秒跑出, 那么如果是由2个 \(2^{k-1}\) 长路径拼成, 那么这个路径的花费为 1
• 为了得到1到n的最小花费, 需要枚举中间点找出任意两点间的最短路径, 最后跑一次 Floyd(或任意最短路算法)

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
const int N = 55;
int g[N][N], dist[N], n, m;
bool f[N][N][66], path[N][N];
bool st[N];

int dijkstra(){
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    for(int i = 0; i < n; i++){
        int t = -1;
        for(int j = 1; j <= n; j++)
            if(!st[j] && (t == -1 || dist[j] < dist[t]))
                t = j;
        st[t] = true;
        for(int j = 1; j <= n; j++)
            dist[j] = min(dist[j], dist[t] + g[t][j]);
    }
    return dist[n];
}

void init(){
    for(int k = 1; k <= 64; k++)
        for(int i = 1; i <= n; i++)
            for(int t = 1; t <= n; t++)
                for(int j = 1; j <= n; j++)
                    if(f[i][t][k - 1] && f[t][j][k - 1]){
                        f[i][j][k] = true;
                        g[i][j] = 1;
                    }
}

int get(int x){
    int cnt = 0;
    while(x){
        if(x & 1) cnt++;
        x >>= 1;
    }
    return cnt;
}

int main(){
    ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
    cin >> n >> m;
    memset(g, 0x3f, sizeof g);
    while(m--){
        int a, b;
        cin >> a >> b;
        g[a][b] = 1;
        f[a][b][0] = true;
    }
    init();
    cout << dijkstra() << endl;
    return 0;
}

P1880 [NOI1995] 石子合并

经典环形区间DP, 破环成链, 复制一次区间接在后面, 区间长度依然为 n

传送门

Solution

#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
const int N = 410, INF = 0x3f3f3f3f;
int w[N], n, s[N];
int f[N][N], g[N][N];
// 两条相同的链模拟环
// 状态表示： f[l][r] 表示从区间 l 到 区间 r 的最小合并费用
// 状态转移： f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);

int main(){
    cin >> n;
    for(int i = 1; i <= n; i ++){
        cin >> w[i];
        w[i + n] = w[i];
    }
    memset(f, 0x3f, sizeof f);
    memset(g, -0x3f, sizeof g);
    for(int i = 1; i <= 2 * n; i++)
        s[i] = s[i - 1] + w[i];
    for(int len = 1; len <= n; len++)
        for(int l = 1; l + len - 1 <= 2 * n; l++){
            int r = l + len - 1;
            if(r > 2 * n) break;
            if(len == 1) f[l][r] = g[l][r] = 0;
            else
                for(int k = l; k <= r; k++){
                    f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
                    g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);
                }
        }
    int max_ = -INF, min_ = INF;
    for(int i = 1; i <= n; i++){
        max_ = max(max_, g[i][i + n - 1]);      // 长度为n的区间，端点差为len - 1
        min_ = min(min_, f[i][i + n - 1]);
    }
    cout << min_ << endl << max_;
    return 0;
}

P3146 [USACO16OPEN]248 G

和下一题只有数据范围不同, 多了一个区间DP的解法

题意

给定一个1*n的地图，在里面玩2048，每次可以合并相邻两个（数值范围1-40），问序列中出现的最大数字的值最大是多少。注意合并后的数值并非加倍而是+1，例如2与2合并后的数值为3。

数据范围
\(1\leq n \leq 248\)

思路

• 区间DP, 定义 \(f[l][r]\) 表示 [l,r] 内合成的最大数
• 转移: if(f[l][k] == f[k + 1][r] && f[l][k]) f[l][r] = max(f[l][r], f[l][k] + 1), 答案取每个状态最大值

Solution

#include<bits/stdc++.h>
typedef long long ll;
#define endl "\n"
using namespace std;
const int N = 250;
int f[N][N];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	int ans = 0;
	for(int i = 1; i <= n; i++){
		cin >> f[i][i];
		ans = max(f[i][i], ans);
	}
	for(int len = 2; len <= n; len ++){
		for(int l = 1; l + len - 1 <= n; l++){
			int r = l + len - 1;
			for(int k = l; k < r; k++){
				if(f[l][k] == f[k + 1][r] && f[l][k]){
					f[l][r] = max(f[l][r], f[l][k] + 1);
					ans = max(ans, f[l][r]);
				}
			}
		}
	}
	cout << ans << endl;
    return 0;
}

P3147 [USACO16OPEN]262144 P (神奇的区间DP)

很有趣的状态定义, 转移和倍增的感觉类似, 还是很神奇的一个区间DP

题意

她被她最近玩的一款游戏迷住了，游戏一开始有 \(n\) 个正整数，\((2\leq n\leq262144)\) ，\(a_i\) 范围在 \(1-40\) 。在一步中，贝西可以选相邻的两个相同的数，

然后合并成一个比原来的大一的数（例如两个7合并成一个8)，目标是使得最大的数最大，请帮助Bessie来求最大值。

思路

• 嗯, DP 题, 然后就不知道咋做了, 可以算出来最大答案为 \(40 + log_2262144 = 58\)
• 状态: \(f[i][j]\) 表示从 j 开始, 能合并到 i 的区间长度, f[a[i]][i] = 1
• 转移: \(f[i][j] = f[i - 1][j] + f[i - 1][j + f[i - 1][j]]\), 后者均存在, 有点类似倍增
• 总的来说, 就是很奇怪, 多见吧

#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
const int N = 3e5;
int f[60][N];		// f[i][j] 从 j 开始合并到的数为 i 的区间长度
// f[i][j] = f[i - 1][j] + f[i - 1][j + f[i - 1][j]];
int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	vector<int> a(n + 1, 0);
	for(int i = 1; i <= n; i++){
		cin >> a[i];
		f[a[i]][i] = 1;
	}
	int ans = 0;
	for(int i = 2; i <= 58; i++){
		for(int j = 1; j <= n; j++){
			if(!f[i][j]){
				if(f[i - 1][j] && f[i - 1][j + f[i - 1][j]])
					f[i][j]= f[i - 1][j] + f[i - 1][j + f[i - 1][j]];
			}
			if(f[i][j])
				ans = i;
			cout << i << " " << j << " " << f[i][j] << endl;
		}
	}
	cout << ans << endl;
    return 0;
} 

P3205 [HNOI2010]合唱队

传统区间DP多加了维度

题意

太长, 给一个传送门

思路

• 由于每进来一次, 都是队列的一个扩展, 和区间DP很类似, 可以用区间DP来思考
• 套路的记录 f[l][r] 表示排好区间 [l,r] 的方案数, 但我们发现, 在新加一个数还与上一次加的数有关, 还需要加维度
• 如何知道上次加的数是什么? 只有两种情况, 在左边或者在右边, 至于最里面的是怎么加的我们已经不用思考了(无后效性)
• 故多加一维 f[l][r][0/1] , 0 表示最后一个数从左边加入, 1 表示最后一个数从右边加入, 判断一下各自大小, 然后很容易写出转移方程, 具体看代码

Solution

#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
const int mod = 19650827;
int f[1010][1010][2];
// f[l][r][0] 表示从左边进， f[l][r][1] 表示从右边进

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	vector<int> a(n + 1, 0);
	for(int i = 1; i <= n; i++)
		cin >> a[i];
	for(int len = 1; len <= n; len++){
		for(int l = 1; l + len - 1 <= n; l++){
			int r = l + len - 1;
			if(l == r){
				f[l][r][0] = 1;
				continue;
			}
			if(a[l] < a[l + 1]) f[l][r][0] += f[l + 1][r][0];
			if(a[l] < a[r]) f[l][r][0] += f[l + 1][r][1];
			if(a[r] > a[l]) f[l][r][1] += f[l][r - 1][0];
			if(a[r] > a[r - 1]) f[l][r][1] += f[l][r - 1][1];
			f[l][r][0] %= mod;
			f[l][r][1] %= mod;
		}
	}
	cout << (f[1][n][0] + f[1][n][1]) % mod << endl;
    return 0;
}

P4170 [CQOI2007]涂色

一道比较常规的区间DP

题意

假设你有一条长度为 5 的木板，初始时没有涂过任何颜色。你希望把它 5 个单位长度分别涂上红、绿、蓝、绿、红色，用一个长度为 5 的字符串表示这个目标：RGBGR。

每次你可以把一段连续的木板涂成一个给定的颜色，后涂的颜色覆盖先涂的颜色。例如第一次把木板涂成 RRRRR，第二次涂成
RGGGR，第三次涂成 RGBGR，达到目标。

用尽量少的涂色次数达到目标。

数据范围
\(1\leq n \leq 50\)

思路

• 区间DP的方式去思考, 定义 \(f[l][r]\) 为染色区间[l,r]最小次数.
• 然后根据题目性质搞一下状态转移吧,像我这种废物只能写70分

#include<bits/stdc++.h>
typedef long long ll;
#define endl "\n"
using namespace std;
const int N = 53;
int f[N][N][2];	// 0 left 1 right

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	string s;
	cin >> s;
	n = s.size();
	s = " " + s;
	memset(f, 0x3f, sizeof f);
	for(int len = 1; len <= n; len++){
		for(int l = 1; l + len - 1 <= n; l++){
			int r = l + len - 1;
			if(l == r){
				f[l][r][0] = 1;
				continue;
			}
			f[l][r][0] = min(f[l][r][0], f[l + 1][r][0] + (s[l] != s[l + 1]));
			f[l][r][0] = min(f[l][r][0], f[l + 1][r][1] + (s[l] != s[r]));
			f[l][r][1] = min(f[l][r][1], f[l][r - 1][0] + (s[l] != s[r]));
			f[l][r][1] = min(f[l][r][1], f[l][r - 1][1] + (s[r] != s[r - 1]));
			if(s[l] == s[r]){
				f[l][r][0] = min(f[l]r][0], f[l + 1][r - 1][0] + (s[l] != s[l + 1]));
				f[l][r][1] = min(f[l][r][1], f[l + 1][r - 1][0] + (s[l] != s[l + 1]));
				f[l][r][0] = min(f[l][r][0], f[l + 1][r - 1][1] + (s[l] != s[r - 1]));
				f[l][r][0] = min(f[l][r][0], f[l + 1][r - 1][1] + (s[l] != s[r - 1]));
			}
		}
	}
	cout << min(f[1][n][0], f[1][n][1]) << endl;

    return 0;
}

P4290 [HAOI2008] 玩具取名

区间DP, 硬找状态表示

传送门

思路

• 一个字母变两个字母, 是一个向左右扩张的模型, 考虑区间DP
• \(f[l][r][a]\) 表示在区间[l,r]能否变成编号 a 的字母,
• if(f[l][k][a] && f[k + 1][r][b] && ok[a][b][c]) f[l][r][c] = 1;

Solution

#include<bits/stdc++.h>
typedef long long ll;
#define endl "\n"
using namespace std;
const int N = 210;
int f[N][N][4];
bool ok[4][4][4];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	unordered_map<char, int> mp;
	mp['W'] = 0, mp['I'] = 1, mp['N'] = 2, mp['G'] = 3;
	int cnt[4];
	for(int i = 0; i < 4; i++)
		cin >> cnt[i];
	for(int i = 0; i < 4; i++){
		for(int j = 0; j < cnt[i]; j++){
			string s;
			cin >> s;
			ok[mp[s[0]]][mp[s[1]]][i] = true;
		}
	}
	string s;
	cin >> s;
	int n = s.size();
	vector<int> v(n + 1, 0);
	for(int i = 0; i < n; i++)
		v[i + 1] = mp[s[i]];
	for(int len = 1; len <= n; len++){
		for(int l = 1; l + len - 1 <= n; l++){
			int r = l + len - 1;
			if(l == r){
				f[l][r][v[l]] = 1;
				continue;
			}
			for(int k = l; k < r; k++){
				for(int c = 0; c < 4; c++)
					for(int a = 0; a < 4; a++)
						for(int b = 0; b < 4; b++)
							if(f[l][k][a] && f[k + 1][r][b] && ok[a][b][c])
								f[l][r][c] = 1;
			}
		}
	}
	bool st[4] = {false}, fl = false;
	for(int i = 0; i < 4; i++){
		if(f[1][n][i])
			fl = true, st[i] = true;
	}
	if(!fl)
		cout << "The name is wrong!\n";
	else{
		string t = "WING";
		for(int i = 0; i < 4; i++){
			if(st[i]){
				cout << t[i];
			}
		}
	}
    return 0;
}

P4310 绝世好题 (带位运算)

非常不错的在位运算基础上的 DP

题意

给一个长度为 \(n\) 的序列 \(a\), 求 \(a\) 的子序列 \(b\) 最长长度, 满足 \(b_i\&b_{i-1} \ne 0\), 其中 \(2\leq i \leq k\)

数据范围
\(1\leq n\leq 100000\)
\(a_i\leq 10^9\)

思路

• 根据 \(b\) 的每一个数只跟前一个数有关, 根据数据大小设置状态
• dp[32], \(dp[i]\) 表示最后一个元素 i 位为 1 的最长序列长度
• 对于 \(a_i\) 来说, 只有该位为 1 时, 才能够对状态进行转移, 先取能够更新的最大值, 然后更新到能更新的状态上.

Solution

#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
int dp[32];	// 到了第 i 位， dp[j] j 位为1的最大序列长度

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	vector<int> a(n + 1, 0);
	for(int i = 1; i <= n; i++)
		cin >> a[i];
	for(int i = 1; i <= n; i++){
		int k = 1;
		for(int j = 0; j < 32; j++){
			if(a[i] >> j & 1)		// 可以转移，记录最大值
				k = max(k, dp[j] + 1);
		}
		for(int j = 0; j < 32; j++)
			if(a[i] >> j & 1)		// 更新所有状态 
				dp[j] = k; // max(k, dp[j]);
	}
	int mx = 0;
	for(int i = 0; i < 32; i++)
		mx = max(mx, dp[i]);
	cout << mx << endl;
    return 0;
}

P4316 绿豆蛙的归宿

图上期望DP, 要按照拓扑序转移状态, 反向建图可以获得从大到小的拓扑序

比较板子, 了解这一类题目做法和拓扑序的获取传送门

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
const int N = 1e5 + 10;
int n, m;
vector<PII> edge[N];
int in[N], out[N];
double f[N];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n >> m;
	for(int i = 0; i < m; i++){
		int a, b, c;
		cin >> a >> b >> c;
		edge[b].pb({a, c});
		out[a]++;
		in[a] ++;
	}
	queue<int> q;
	q.push(n);
	while(q.size()){
		auto t = q.front();
		q.pop();
		for(auto v: edge[t]){
			f[v.x] += (double)(v.y + f[t])  / (double)out[v.x];
			in[v.x --;
			if(!in[v.x])
				q.push(v.x);
		}
	}
	cout << fixed << setprecision(2) << f[1];
    return 0;
}

\(\color{#48D}{提高+/省选-}\)

CF1265E Beautiful Mirrors

期望dp倒推公式, 发现需要前置变量, 再从前置变量顺推发现可以推到答案

小C有\(N\) 个从编号分别为\(1\) 到\(N\) 的镜子。她每天都会问一面镜子：“我漂亮吗？”而对于第\(i\) 面镜子，有\(p_i\)
\((1\leq i\leq n)\) 的概率告诉小C很漂亮。

她从第一面镜子开始，一个接一个的问镜子。每一天，对于她问的第 \(i\) 个镜子，有两种情况：

如果第 \(i\) 个镜子告诉小C她很漂亮：若此时 \(i=n\) ，则小C就会开心到极点，停止对镜子的询问。

否则，她第二天就会询问第\(i+1\) 个镜子如果第 \(i\) 个镜子并没有告诉小C她很漂亮，她就会很伤心，第二天重新从第 \(1\) 个镜子开始询问。

你需要计算小C询问完所有镜子后开心到极点的期望天数。若期望天数可被表示为最简分数 \(p/q\) ，则你需要输出的是 \(p⋅q^−1\) (\(\mod 998244353\))。

数据范围
\(1\leq n \leq 2 * 10^5\)
\(1\leq p_i \leq 100\)

思路

• 先按照期望逆推状态 \(f[i]\) 表示 \(i\) 点到极点的期望天数, \(f_i = 1 + p_i*f_{i + 1} + (1 - p_i) * f_1\)
• 发现需要用到 \(f_1\), 考虑 \(f_1 = 1 + p_1 * f_2 + (1-p_1) * f_1\)
• 因为我们要求 \(f_1\), 把 \(f_2\) 放到左边, 即 \(f_2 = f_1 - \frac{1}{p_1}\)
• 再看 \(f_2 = 1 + p_2 * f_3 + (1 - p_2) * f_1\) , 化简 \(f_1 = \frac{1}{p_2} + \frac{1}{p_1*p_2} + f_3\), 当然还是要把 \(f_3\) 放在左边继续代入下一个式子
• 从上点可以发现规律了, \(f_1 = f_{i + 1} + \frac{1}{f_i} + \frac{1}{f_i*f_{i-1}} + \cdots + \frac{1}{f_i*f_{i-1}*\cdots *f_1}\)
• \(f_{n+1} = 0\) , 所以很容易计算 \(f_1\)

Solution

#include<bits/stdc++.h>
typedef long long ll;
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
const int N = 2e5 + 10, mod = 998244353;
int f[N];
ll qmi(ll a, ll k, int mod){
	ll res = 1;
	while(k){
		if(k & 1)
			res = res * a % mod;
		a = a * a % mod;
		k >>= 1;
	}
	return res;
}

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	ll tmp = 1, ans = 0;
	vector<ll> p(n + 1, 0);
	for(int i = 1; i <= n; i++){
		cin >> p[i];
	}
	for(int i = n; i >= 1; i--){
		tmp = tmp * p[i] % mod;
		ans = (ans + qmi(100, n - i + 1, mod) * qmi(tmp, mod - 2, mod) % mod) % mod;
	}
	cout << ans << endl;
    return 0;
}

P1070 [NOIP2009 普及组] 道路游戏

普及组题目, 数据不大, n^3 能卡过, 有单调队列优化方式, 但是没找到合适的题解, 有机会来补

题目复杂->传送门

思路

• 见代码注释, 主要采用顺推的方式, 同样无后效性

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
int n, m, p;
const int N = 1010;
int f[N], cost[N], s[N][N];		// f[i] 表示在时刻 i 获得最大值
int w[N][N];		// w[i][j] j时刻到达工厂i 的价值
// 顺推更新状态，复杂度接近 O(n^3)
int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n >> m >> p;
	for(int i = 1; i <= n; i++)
		for(int j = 1; j <= m; j++)
			cin >> w[j][i];
	for(int i = 1; i <= n; i++)
		cin >> cost[i];
	memset(f, -0x3f, sizeof f);
	f[0] = 0;
	for(int i = 1; i <= m; i++){		
		for(int j = 1; j <= n; j++){		// 循环起点
			int tmp = f[i - 1] - cost[j];
			for(int k = 0; k + i <= m && k < p; k++){		// 循环步数
				int ed = (j + k > n) ? j + k - n : j + k;		// 处理下一步是否有环
				tmp += w[i + k][ed];		// 计算价值 
				f[i + k] = max(f[i + k], tmp);		// 顺推更新状态
			}
		}
	}
	cout << f[m] << endl;
    return 0;
}

P1220 关路灯

区间DP, 需要好好思考的状态设计.

题意

某一村庄在一条路线上安装了 \(n\) 盏路灯，每盏灯的功率有大有小（即同一段时间内消耗的电量有多有少）。老张就住在这条路中间某一路灯旁，他有一项工作就是每天早上天亮时一盏一盏地关掉这些路灯。

为了给村里节省电费，老张记录下了每盏路灯的位置和功率，他每次关灯时也都是尽快地去关，但是老张不知道怎样去关灯才能够最节省电。他每天都是在天亮时首先关掉自己所处位置的路灯，然后可以向左也可以向右去关灯。开始他以为先算一下左边路灯的总功率再算一下右边路灯的总功率，然后选择先关掉功率大的一边，再回过头来关掉另一边的路灯，而事实并非如此，因为在关的过程中适当地调头有可能会更省一些。

现在已知老张走的速度为 \(1m/s\) ，每个路灯的位置（是一个整数，即距路线起点的距离，单位：m、功率（W），老张关灯所用的时间很短而可以忽略不计。

请你为老张编一程序来安排关灯的顺序，使从老张开始关灯时刻算起所有灯消耗电最少（灯关掉后便不再消耗电了）。

数据范围
\(1\leq n \leq 50\)

思路

关灯不需要额外的时间，经过了灯就关了。但是可能折返回去关某一个大灯会比继续往下走关接下来的一个小灯更优，那么可以得到两种状态（沿着当前方向继续往下走，改变方向回去关灯）。
那么要设计的状态转移方程中肯定有两种方案（折返的，不撞墙不回头的), 又因为如果想要关某一区间的灯的过程中耗能最小，所以可以转换成一个个区间来写：

• 所以设计状态 \(f[l][r][0/1]\) , 关完了 [l,r] 的灯，站在l/r上
• 然后在更新 f[l][r][0/1] 时, 看上一个小区间的左右端点来转移, 此时有无后效性, 对于更小的区间如何求得的, 我们并不关心, 具体转移方程见代码

Solution

#include<bits/stdc++.h>
typedef long long ll;
#define endl "\n"
using namespace std;
const int N = 55;
int f[N][N][2], n, pos[N], c;		// f[l][r][0/1] 关完了 [l,r] 的灯，站在l/r上
int dist[N][N], s[N];
// f[l][r][0] = max(f[l + 1][r][1] + cost, f[l + 1][r][1] + cost)

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n >> c;
	memset(f, 0x3f, sizeof f);
	f[c][c][0] = f[c][c][1] = 0;
	for(int i = 1; i <= n; i++)
		cin >> pos[i] >> s[i];
	for(int i = 1; i <= n; i++){
		s[i] = s[i - 1] + s[i];
	}
	for(int len = 2; len <= n; len++){
		for(int l = 1; l + len - 1 <= n; l++){
			int r = l + len - 1;
			f[l][r][0] = min(f[l + 1][r][0] + (pos[l + 1] - pos[l]) * (s[l] + s[n] - s[r]),
				f[l + 1][r][1] + (pos[r] - pos[l]) * (s[l] + s[n] - s[r]));
			f[l][r][1] = min(f[l][r - 1][1] + (pos[r] - pos[r - 1]) * (s[n] - s[r - 1] + s[l - 1]),
				f[l][r - 1][0] + (pos[r] - pos[l]) * (s[n] - s[r - 1] + s[l - 1]));
		}
	}
	cout << min(f[1][n][0], f[1][n][1]) << endl;
    return 0;
}

P1654 OSU!

期望DP经典题, 推导长度立方的期望

题意

osu 是一款群众喜闻乐见的休闲软件。

我们可以把osu的规则简化与改编成以下的样子:

一共有n次操作，每次操作只有成功与失败之分，成功对应1，失败对应0，n次操作对应为1个长度为n的01串。在这个串中连续的 \(X\) 个 \(1\) 可以贡献 \(X^3\) 的分数，这x个1不能被其他连续的1所包含（也就是极长的一串1，具体见样例解释）

现在给出n，以及每个操作的成功率，请你输出期望分数，输出四舍五入后保留1位小数。

数据范围
\(N<=100000\)

思路

• 直接找期望比较难, 需要套路
• 先考虑第 i 位维护长度一次方的期望, \(x1[i] = (x1[i - 1] + 1) * p[i]\),
• 再考虑第 i 位维护长度二次方的期望, \(x2[i] = (x2[i - 1] + 2 * x[i - 1] + 1) * p[i]\)
• 再来维护第 i 位维护长度三次方的期望, \(x3[i] = (x3[i - 1] + 3 * x2[i - 1] + 3 * x1[i - 1] + 1) * p[i]\)
• 由于答案是对整个序列的长度期望, \(f=x3, f[i] = (f[i - 1] + 3 * x2[i - 1] + 3 * x1[i - 1] + 1) * p[i] + f[i - 1] * (1 - p[i])\)
• 最后滚动数组优化空间

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
const int N = 1e5 + 10;
double p[N];
int n;

int main(){
	scanf("%d", &n);
	for(int i = 1; i <= n; i++)
		scanf("%lf", &p[i]);
	double x1 = 0, x2 = 0, ans = 0;
	for(int i = 1; i <= n; i++){
		ans = ans + (3 * x2 + 3 * x1 + 1) * p[i];
		x2 = (x2 + 2 * x1 + 1) * p[i];
		x1 = (x1 + 1) * p[i];
	}
	printf("%.1lf\n", ans);
    return 0;
}

P4342 [IOI1998]Polygon

经典区间DP, 但由于进行算术运算涉及正负号, 需要记录区间的最大值和最小值来转移

题意

传送门

思路

• 常规区间DP做法, 破环成链, 然后记录 \(f[l][r][0/1]\) 为区间的最值
• 转移: 根据符号进行转移, 对于乘法时的转移, 可能一正一负, 两正, 两负相乘都可能更新最大值, 所以都要转移一下
• 最后枚举哪个边被破坏后的结果和答案一样就可以输出所有的边了

Solution

#include<bits/stdc++.h>
typedef long long ll;
#define endl "\n"
#define INF 2e18
using namespace std;
const int N = 110;
ll f[N][N][2], n;  // 0 最小值， 1 最大值
ll a[N];
bool tail[N];

void mx(ll& a, ll b){
	a = max(a, b);
}

void mi(ll& a, ll b){
	a = min(a, b);
}

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n;
	for(int i = 1; i <= 2 * n; i++){
		if(i & 1){
			char c;
			cin >> c;
			if(c == 'x'){
				if(!(i / 2))
					tail[n] = true;
				else
					tail[i / 2] = true;
			}
		}
		else{
			cin >> a[i / 2];
		}
	}
	for(int i = 1; i <= n; i++){
		a[i + n] = a[i];
		tail[i + n] = tail[i];
	}
	for(int len = 1; len <= n; len++){
		for(int l = 1; l + len - 1 <= 2 * n; l++){
			int r = l + len - 1;
			f[l][r][0] = INF;
			f[l][r][1] = -IF;
			if(l == r){
				f[l][r][0] = f[l][r][1] = a[l];
				continue;
			}
			for(int k = l; k < r; k++){
				if(tail[k]){
					mx(f[l][r][1], f[l][k][1] * f[k + 1][r][1]);
					mx(f[l][r][1], f[l][k][0] * f[k + 1][r][0]);
					mx(f[l][r][1], f[l][k][1] * f[k + 1][r][0]);
					mx(f[l][r][1], f[l][k][0] * f[k + 1][r][1]);
					mi(f[l][r][0], f[l][k][1] * f[k + 1][r][1]);
					mi(f[l][r][0], f[l][k][0] * f[k + 1][r][0]);
					mi(f[l][r][0], f[l][k][1] * f[k + 1][r][0]);
					mi(f[l][r][0], f[l][k][0] * f[k + 1][r][1]);
				}
				else{
					f[l][r][0] = min(f[l][r][0], f[l][k][0] + f[k + 1][r][0]);
					f[l][r][1] = max(f[l][r][1], f[l][k][1] + f[k + 1][r][1]);
				}
			}
		}
	}
	ll ans = -2e18;
	for(int i = 1; i <= n; i++){
		ans = max(ans, f[i][i + n - 1][1]);
	}
	cout << ans << endl;
	for(int i = 1; i <= n; i++){
		if(f[i][i + n - 1][1] == ans)
			cout << i << " ";
	}
    return 0;
}

P4550 收集邮票

推两次期望, 一次是次数, 一次是费用, 因为费用与次数相关

题意

有 \(n\) 种不同的邮票，皮皮想收集所有种类的邮票。唯一的收集方法是到同学凡凡那里购买，每次只能买一张，并且买到的邮票究竟是 \(n\) 种邮票中的哪一种是等概率的，概率均为 \(1/n\) 。但是由于凡凡也很喜欢邮票，所以皮皮购买第
\(k\) 次邮票需要支付 \(k\) 元钱。

现在皮皮手中没有邮票，皮皮想知道自己得到所有种类的邮票需要花费的钱数目的期望。

数据范围
\(1\leq n \leq 10000\)

思路

• 首先是对次数的期望进行dp, \(f[i]\) 表示已经有了 i 张邮票集满的次数的期望
• \(f[i] = \frac{i}{n} * (f[i] + 1) + (1 - \frac{i}{n}) * (f[i + 1] + 1)\)
• 因为答案和费用相关, 设 \(g[i]\) 表示已经有了 i 张邮票距离集满的期望费用
• \(g[i] = \frac{i}{n} * (g[i] + f[i] + 1) + \frac{n-i}{n} * (g[i + 1] + f[i + 1] + 1)\) , 理解为 g[i] 为节点 i 到 n 的期望边权, 对应边权为 f[i] + 1 , 求 0 -> n 的期望边权
• 即, \(g[i] = \frac{i}{n-i} * f[i] + g[i + 1] + f[i + 1] + \frac{n}{n - i}\)
• \(f[n] = g[n] = 0\) , 然后倒推即可

Solution

#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
const int N = 10010;
double f[N];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	double f = 0, g = 0, f_pre = 0;
	int n;
	cin >> n;
	for(int i = n - 1; i >= 0; i--){
		f = f_pre + (double)n / (n - i);
		g = (double) i / (n - i) * f + f_pre + g + (double) n / (n - i);
		f_pre = f;
	}
	cout << fixed << setprecision(2) << g << endl;
    return 0;
}

\(\color{#83C}{省选+/NOI-}\)

P3232 [HNOI2013]游走

期望DP, 高斯消元消除后效性

题意

给定一个 \(n\) 个点 \(m\) 条边的无向连通图，顶点从 \(1\) 编号到 \(n\)，边从 \(1\) 编号到 \(m\)。

小 Z 在该图上进行随机游走，初始时小 Z 在 \(1\) 号顶点，每一步小 Z 以相等的概率随机选择当前顶点的某条边，沿着这条边走到下一个顶点，获得等于这条边的编号的分数。当小 Z 到达 \(n\) 号顶点时游走结束，总分为所有获得的分数之和。 现在，请你对这 \(m\) 条边进行编号，使得小 Z 获得的总分的期望值最小。

数据范围

• 对于 \(30\%\) 的数据，保证 \(n\leq 10\)。
• 对于 \(100\%\) 的数据，保证 \(2\leq n \leq 500\)， \(1 \leq m \leq 125000\)，\(1 \leq u, v \leq n\)，给出的图无重边和自环，且从 \(1\) 出发可以到达所有的节点。

思路

• 随意推导发现, 递推不满足后效性, 并且考虑边的话, 数量过大, 考虑从点的角度出发
• 设 \(f[i]\) 表示到 \(i\) 点的期望次数, 那么 \(f[i] = \Sigma_{j = 1}^{j\ne n} f[j]/deg[j] + (i == 1)\; and\; i\ne n\) , 所以有 \(n-1\) 个方程, \(n-1\) 个未知数, 可以高斯消元求解
• 由于到了 \(n\) 点就不再走了, 所以抠出 \(n\) 点.
• 对于每条边经过次数为 \(f[u]/deg[u] + f[v]/deg[v]\; and\; u\ne n, v\ne n\) , 排序从小到大贪心编号即可

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef std::pair<int, int> PII;
typedef double db;
#define pb push_back
#define endl "\n"
using namespace std;
const int N = 510, M = 125010;
const double eps = 0;
long double a[N][N];	
vector<int> edge[N];
PII e[M];
int n, deg[N], m;

int gauss(int n){
    int c, r;
    for(c = 1, r = 1; c <= n; c ++){
        int t = r;
        for(int i = r; i <= n; i++) 	// 找到绝对值最大的一行
            if(fabs(a[i][c]) > fabs(a[t][c]))
                t = i;
        if(fabs(a[t][c]) < eps) continue;
        for(int i = c; i <= n + 1; i++) swap(a[t][i], a[r][i]); // 交换到第r行枚举列
        for(int i = n + 1; i >= c; i--) a[r][i] /= a[r][c]; // 主元系数为1，注意从后往前推
        for(int i = r + 1; i <= n; i++)	// 将下面每行减去 第r行的 a[i][c] 倍
            if(fabs(a[i][c]) > eps)
                for(int j = n + 1; j >= c; j--)
                    a[i][j] -= a[i][c] * a[r][j];
        r ++;   // 秩+1
    }
    if(r <= n){  // 秩 < n
        for(int i = r; i <= n; i++)
            if(fabs(a[r][n + 1]) > eps)     // 0=x (x!=0)，无解
                return 2;           // 无解
        return 1;       // 无穷解
    }
    for(int i = n; i >= 1; i--)     // 倒推算出每个x  
        for(int j = i + 1; j <= n; j++){ // a[i][n] -= 枚举首元之后的系数 a[i][j] * 对应的x_n的值 a[j][n]
            a[i][n + 1] -= a[i][j] * a[j][n + 1];
        }
    return 0;
}

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n >> m;
	for(int i = 0; i < m; i++){
		int u, v;
		cin >> u >> v;
		e[i] = {u, v};
		edge[u].pb(v), edge[v].pb(u);
		deg[u]++, deg[v]++;
	}
	for(int i = 1; i <= n; i++){
		a[i][i] = 1;
		for(auto v: edge[i])
			if(v != n)
				a[i][v] = -1.0 / deg[v];
	}
	a[1][n] = 1;
	gauss(n - 1);
	vector<long double> v(m, 0);
	for(int i = 0; i < m; i++){
		auto t = e[i];
		if(t.x != n) v[i] += a[t.x][n] / deg[t.x];
		if(t.y != n) v[i] += a[t.y][n] / deg[t.y];
	}
	sort(v.begin(), v.end());
	long double ans = 0;
	for(int i = 0; i < m; i++){
		ans += v[i] * (m - i);
	}
	cout << fixed << setprecision(3) << ans << endl;
    return 0;
}

\(\color{#115}{NOI/NOI+/CTSC}\)

数据结构

\(\color{#E91}{普及-}\)

\(\color{#FC1}{普及/提高-}\)

P1774 最接近神的人

简单题, 一个结论, 通过相邻交换使得数列递增的最小操作次数是数列中的逆序对个数

传送门

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;

template<class T>
struct BIT {
	int n;
	vector<T> B;
	BIT(){};
	BIT(int _n) : n(_n), B(_n + 1, 0) {}
	void init(int _n){
		n = _n;
		B.resize(_n + 1);
	}
	inline int lowbit(int x) { return x & (-x); }
	void add(int x, T v) {
		for(int i = x; i <= n; i += lowbit(i)) B[i] += v;
	}
	T ask(int x) {
		T res = 0;
		for(int i = x; i; i -= lowbit(i)) res += B[i];
		return res;
	}
};
vector<ll> alls;

int find(ll x){
	return lower_bound(arr(alls), x) - alls.begin() + 1;
}

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	BIT<ll> bt(n);
	ll ans = 0;
	vector<ll> a;
	for(int i = 0; i < n; i++){
		ll x;
		cin >> x;
		a.pb(x), alls.pb(x);
	}
	sort(arr(alls));
	alls.erase(unique(arr(alls)), alls.end());
	for(int i = 0; i < n; i++){
		a[i] = find(a[i]);
		ans += i - bt.ask(a[i]);
		bt.add(a[i], 1);
	}
	cout << ans << endl;
    return 0;
}

\(\color{#6B1}{普及+/提高}\)

CF547B Mike and Feet

使用单调栈经典操作, 可以记录左右比 \(a_i\) 小的第一个数, 前缀最大值统计答案

题意

找出长度为 \(1-n\) 中的滑动窗口最小值的最大值

数据范围
\(1\leq n \leq 2 * 10^5\)
\(1\leq a_i \leq 2 * 10^5\)

思路

• 需要对每个数找到左边第一个小于 \(a_i\) 和 右边第一个小于 \(a_i\) 的数.
• 发现就是单调栈的一个经典使用 (鬼知道我想了一个权值线段树)
• 每个数可以更新长度为 1 ~ (r[i] - l[i] - 1) 的区间的答案, 由于需要最大值, 用前缀(实际后缀) 最大值来统计答案,实际见代码

Solution

#include<bits/stdc++.h>
typedef long long ll;
#define endl "\n"
using namespace std;
const int N = 2e5 + 10;
int l[N], r[N], ans[N];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n;
	cin >> n;
	vector<int> a(n + 1, 0);
	for(int i = 1; i <= n; i++)
		cin >> a[i];
	int stk[N], tt = 0;
	for(int i = 1; i <= n; i++){
		while(a[stk[tt]] >= a[i]) tt--;
		l[i] = stk[tt];
		if(!l[i]) l[i] = 0;
		stk[++tt] = i;
	}
	tt = 0;
	for(int i = n; i >= 1; i--){
		while(a[stk[tt]] >= a[i]) tt--;
		r[i] = stk[tt];
		if(!r[i]) r[i] = n + 1;
		stk[++tt] = i;
	}
	for(int i = 1; i <= n; i++){
		int len = r[i] - l[i] - 1;
		// cout << i << " " << l[i] << " " << r[i]<<endl;
		ans[len] = max(ans[len], a[i]);
	}
	int mx = 0;
	for(int i = n; i >= 1; i--){
		ns[i] = max(mx, ans[i]);
		mx = max(ans[i], mx);
	}
	for(int i = 1; i <= n; i++)
		cout << ans[i] << " ";
    return 0;
}

P1253 [yLOI2018] 扶苏的问题

线段树标记之间不仅要考虑优先性, 还有可能一个标记的更新会对另一个标记产生作用

题意

给定一个长度为 \(n\) 的序列 \(a\)，要求支持如下三个操作：

给定区间 \([l,r]\) ，将区间内每个数都修改为 \(x\) 。
给定区间 \([l,r]\) ，将区间内每个数都加上 \(x\) 。
给定区间 \([l,r]\) ，求区间内的最大值。

数据范围
\(1\leq n,q \leq 10^6\)
\(|a_i|, |x|\leq 10^9\)

思路

• 常规操作,维护两个lazy标记 same 与 add
• 注意更新 add 时, 如果节点 same 标记不为null, 则将 tr[u].same += add, 否则 tr[u].add+=add
• 更新 same 时, 将 add 标记清空
• 初始时, same != 0 , 需要在 build() 中 pushup() 后特别初始化 tr[u].same = INF

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
const int N = 1e6 + 10;
ll INF = -2e18;
int a[N], tot;

struct SegTree{
    #define ls u << 1
    #define rs u << 1 | 1
    struct T{
        int l, r;
        ll mx, add, same;
        void init(){
        	mx = a[l];
        	add = 0;
        	same = INF;
        }
    };
    vector<T> tr;
    SegTree() {}
    SegTree(int n): tr((n + 1) << 2) {build(1, 1, n);};
    void pushup(int u){
    	tr[u].mx = max(tr[ls].mx, tr[rs].mx);
    }
    void pdate(T& rt, ll same, ll add){
    	if(add){		// 更新加标记，如果same标记存在要对same标记更新，否则对add标记更新
			rt.mx += add;
    		if(rt.same != INF)
    			rt.same += add;
    		else
    			rt.add += add;
    	}
    	else if(same != INF){
    		rt.mx = same;
    		rt.same = same;
    		rt.add = 0;		// 更新了same标记，add操作归0
    	}
    }
    void pushdown(int u){
    	ll same = tr[u].same, add = tr[u].add;
    	if(same != INF){
	    	update(tr[ls], same, 0);
	    	update(tr[rs], same, 0);
	    	tr[u].same = INF, tr[u].add = 0;
    	}
    	else if(add){
	    	update(tr[ls], INF, add);
	    	update(tr[rs], INF, add);
	    	tr[u].add = 0;
    	}
    }
    void build(int u, int l, int r){        // 建立线段树，(节点编号，节点区间左端点，节点区间右端点)
        tr[u] = (T){l, r}; 
    	if(tr[u].l > r || tr[u].r < l) return;
        if(l == r){
            tr[u].init();
            return;
        }
        int mid = (l + r) >> 1;
        build(ls, l, mid), build(rs, mid + 1, r);       
        pushup(u);
        tr[u].add = 0;
        tr[u].same = INF;
    }   
    ll query(int u, int l, int r){
    	if(tr[u].l > r || tr[u].r < l) return INF;
        if(tr[u].l >= l && tr[u].r <= r){
        	return tr[u].mx;
        }  
        else{
            pushdown(u);        // 递归分裂前pushdown
            int mid = (tr[u].l + tr[u].r) >> 1;
            ll res = INF;
            if(l <= mid) res = query(ls, l, r);
            if(r > mid) res = max(res, query(rs, l, r));
            return res;
        }
    }
    void modify(int u, int l, int r, ll v, int t){    // 区间修改
    	if(tr[u].l > r || tr[u].r < l) return;
        if(tr[u].l >= l && tr[u].r <= r){       // 注意区间修改的递归出口
        	if(t)
        		update(tr[u], v, 0);
        	else
        		update(tr[u], INF, v);
            return ;
        }
        pushdown(u);        // 递归分裂前 pushdown  
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(l <= mid) modify(ls, l, r, v, t);
        if(r > mid) modify(rs, l, r, v, t);
        pushup(u);
    }
};

int main(){
	int n, q;
	scanf("%d%d", &n, &q);
	for(int i = 1; i <= n; i++)
		scanf("%d", &a[i]);
	SegTree tr(n);
	while(q--){
		int op, l, r;
		ll x;
		scanf("%d%d%d", &op, &l, &r);
		if(op == 1){
			scanf("%lld", &x);
			tr.modify(1, l, r, x, 1);
		}
		else if(op == 2){
			scanf("%lld", &x);
			tr.modify(1, l, r, x, 0);
		}
		else{
			printf("%lld\n", tr.query(1, l, r));
		}
	}
    return 0;
}

\(\color{#48D}{提高+/省选-}\)

P2163 [SHOI2007]园丁的烦恼

二维数点基础

题意

第一行有两个整数 \(n, m\)，分别表示树木个数和询问次数。

接下来 \(n\) 行，每行两个整数 \(x, y\)，表示存在一棵坐标为 \((x, y)\) 的树。有可能存在两棵树位于同一坐标。

接下来 \(m\) 行，每行四个整数 \(a, b, c, d\)，表示查询以 \((a, b)\) 为左下角，\((c, d)\) 为右上角的矩形内部（包括边界）有多少棵树。

对于每个查询，输出一行一个整数表示答案。

数据范围

• 对于 \(30\%\) 的数据，保证 \(n, m \leq 10\)。
• 对于 \(100\%\) 的数据，保证 \(0 \leq n \leq 5 \times 10^5\)，\(1 \leq m \leq 5 \times 10^5\)，\(0 \leq x, y, a, b, c, d \leq 10^7\)，\(a \leq c\)，\(b \leq d\)。

思路

• 基础二维数点，询问一个子矩阵内数目，可以有类似于二维前缀和的思想。
• 将询问拆成四个虚点，询问以 (0,0) 为左下角的矩阵子树数目可以容斥得原答案。
• 将询问和加点一起处理，排序消除某一维的影响
  • 第一关键字：X坐标
  • 第二关键字：Y坐标
  • 第三关键字：优先加点
• 记录答案映射输出即可, 特判特殊情况

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/
int n, m;
// a <= x <= c, b <= y <= d;
vector<int> alls;

template<class T>
struct BIT {
    int n;
    vector<T> B;
    BIT(){};
    BIT(int _n) : n(_n), B(_n + 1, 0) {}
    void init(int _n) {
            n = _n;
            B.resize(_n + 1);
    }
    inline int lowbit(int x) { return x & (-x); }
    void add(int x, T v) {
            for (int i = x; i <= n; i += lowbit(i)) B[i] += v;
    }
    T ask(int x) {
            T res = 0;
            for (int i = x; i; i -= lowbit(i)) res += B[i];
            return res;
    }
};

int find(int x){
    return lower_bound(arr(alls), x) - alls.begin() + 1;
}

struct Q{
    int a, b, c, d;
};

struct A{
    int op, x, y, id;
    bool operator < (const A& a) const {
        if (x != a.x)
            return x < a.x;
        if (y != a.y)
            return y < a.y;
        return id < a.id;
    }
};

int main() {
    scanf("%d%d", &n, &m);
    if (n == 0) {
        for (int i = 0; i < m; i++)
            printf("0\n");
        return 0;
    }
    if (m == 0) {
        printf("0\n");
        return 0;
    }
    vector<PII> p(n);
    for (int i = 0; i < n; i++) {
        scanf("%d%d", &p[i].x, &p[i].y);
        alls.pb(p[i].y);
    }
    vector<Q> q(m);
    for (int i = 0; i < m; i++) {
        scanf("%d%d%d%d", &q[i].a, &q[i].b, &q[i].c, &q[i].d);
        alls.pb(q[i].b);
        alls.pb(q[i].d);
    }
    sort(arr(alls));
    alls.erase(unique(arr(alls)), alls.end());
    int sz = alls.size();
    BIT<int> bt(sz);
    int idx = 0;
    vector<A> query;
    for (int i = 0; i < n; i++){
        p[i].y = find(p[i].y);
        query.pb({1, p[i].x, p[i].y, idx++});
    }
    vector<array<int, 4>> res(m);
    for (int i = 0; i < m; i++) {
        int x1 = q[i].a, y1 = find(q[i].b);
        int x2 = q[i].c, y2 = find(q[i].d);
        for (int j = 0; j < 4; j++)
            res[i][j] = idx + j;
        query.pb({2, x2, y2, idx});
        query.pb({2, x1 - 1, y2, idx + 1});
        query.pb({2, x2, y1 - 1, idx + 2});
        query.pb({2, x1 - 1, y1 - 1, idx + 3});
        idx += 4;
    }
    vector<int> ans(idx + 1, 0);
    sort(arr(query));
    for (int i = 0; i < idx; i++) {
        if (query[i].op == 1) 
            bt.add(query[i].y, 1);
        else {
            ans[query[i].id] = bt.ask(query[i].y);
        }
    }
    for (int i = 0; i < m; i++)
        printf("%d\n", ans[res[i][0]] - ans[res[i][1]] - ans[res[i][2]] + ans[res[i][3]]);
    return 0;
}

P4145 上帝造题的七分钟 2 / 花神游历各国

势能线段树、区间开方

题意

对序列进行区间开方（下取整）、区间求和

数据范围
\(1\leq n \leq 1e5\)
\(1\leq a_i \leq 1e12\)

思路

• 因为每个 \(a_i\) 最多开方 \(log(1e12) = 40\) 左右，完全可以将区间开方改成单点暴力，当区间 \(mx\leq 1\) 直接 return modify 操作

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/
const int N = 1e5 + 10;
ll a[N];

struct SegTree{
    #define ls u << 1
    #define rs u << 1 | 1
    const static int maxn = 1000010;
    struct T{
        int l, r;
        ll v, mx;
    }tr[maxn << 2];
    void pushup(int u){
        tr[u].v = tr[ls].v + tr[rs].v;
        tr[u].mx = max(tr[ls].mx, tr[rs].mx);
    }
    void build(int u, int l, int r){        // 建立线段树，(节点编号，节点区间左端点，节点区间右端点)
        tr[u].l = l, tr[u].r = r;
        if(tr[u].l == tr[u].r){
            tr[u].v = tr[u].mx = a[l];
            return;
        }
        int mid = (l + r) >> 1;
        build(ls, l, mid), build(rs, mid + 1, r);       
        pushup(u);
    }   
    ll query(int u, int l, int r){
        if(tr[u].l >= l && tr[u].r <= r){
            return tr[u].v;
        }  
        else{
            int mid = (tr[u].l + tr[u].r) >> 1;
            ll res = 0;
            if(l <= mid) res = query(ls, l, r);
            if(r > mid) res += query(rs, l, r);
            return res;
        }
    }
    void modify(int u, int l, int r){    // 区间修改
        if (tr[u].l == tr[u].r && tr[u].l >= l && tr[u].r <= r) {
            tr[u].v = (ll)sqrt(tr[u].v);
            tr[u].mx = (ll)sqrt(tr[u].mx);
            return ;
        }
        if (tr[u].mx <= 1) return;
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(l <= mid) modify(ls, l, r);
        if(r > mid) modify(rs, l, r);
        pushup(u);
    }
}tr;

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n, m;
    cin >> n;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    cin >> m;
    tr.build(1, 1, n);
    while (m--) {
        int k, l, r;
        cin >> k >> l >> r;
        if (l > r) swap(l, r);
        if (!k) {
            tr.modify(1, l, r);
        }
        else {
            cout << tr.query(1, l, r) << endl;
        }
    }
    return 0;
}

P4513 小白逛公园

求区间最大连续子序列和
题意

对长度为 \(n(n \leq 5 * 10^t)\) 序列进行单点修改和区间 \([l,r]\) 查询最大连续子序列和

思路

• 和求全序列最大子序列和大致相同
• 在query后进行类似 pushup 一样的操作来返回结果

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
const int N = 5e5 + 10;
const ll INF = 2e18;
int a[N];
struct R{
	ll lmx, rmx, mx, v;
};

struct SegTree{
    #define ls u << 1
    #define rs u << 1 | 1
    struct T{
        int l, r;
        ll v, lmx, rmx, mx;
        void init(){
        	v = a[l];
        	lmx = rmx = v;
        	mx = a[l];
        }
    };
    vector<T> tr;
    SegTree() {}
    SegTree(int n): tr((n + 1) << 2) {build(1, 1, n);};
    void pushup(int u){
    	tr[u].v = tr[ls].v + tr[rs].v;
    	tr[u].lmx = max(tr[ls].v + tr[rs].lmx, tr[ls].lmx);
    	tr[u].rmx = max(tr[rs].v + tr[ls].rmx, tr[rs].rmx);
    	tr[u].mx = max(max(tr[ls].mx, tr[rs].mx), tr[ls].rmx + tr[rs].lmx);
    }
    void build(int u, int l, int r){        // 建立线段树，(节点编号，节点区间左端点，节点区间右端点)
        tr[u] = (T){l, r}; 
        if(l == r){
            tr[u].init();
            return;
        }
        int mid = (l + r) >> 1;
        build(ls, l, mid), build(rs, mid + 1, r);       
        pushup(u);
    }   
    R query(int u, int l, int r){
        if(tr[u].l >= l && tr[u].r <= r){
        	return {tr[u].lmx, tr[u].rmx, tr[u].mx, tr[u].v};
        }  
        else{
            int mid = (tr[u].l + tr[u].r) >> 1;
            R lt, rt, res;
            lt.lmx = -INF, rt.lmx = -INF;
            if(l <= mid) lt = query(ls, l, r);
            if(r > mid) rt = query(rs, l, r);
            if(lt.lmx == -INF || rt.lmx == -INF){
            	if(lt.lmx == -INF)
            		return rt;
            	else
            		return lt;
            }
            res.v = lt.v + rt.v;
            res.lmx = max(lt.lmx, lt.v + rt.lmx);
            res.rmx = max(rt.rmx, rt.v + lt.rmx);
            res.mx = max(max(lt.mx, rt.mx), lt.rmx + rt.lmx);
            return res;
        }
    }
    void modify(int u, int pos, int v){         // 单点修改, (节点编号，查询点下标，更改值)
        if(tr[u].l == pos && tr[u].r == pos){   
            tr[u].v = tr[u].mx = v;
            tr[u].lmx = tr[u].rmx = v;
            return ;
        } 
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(pos <= mid) modify(ls, pos, v);     
        else modify(rs, pos, v);               
        pushup(u);          // 子节点变化，pushup往父节点更新信息
    }   
};


int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	int n, m;
	cin >> n >> m;
	for(int i = 1; i <= n; i++)
		cin >> a[i];
	SegTree tr(n);
	while(m--){
		int k, l, r, p, s;
		cin >> k;
		if(k == 1){
			cin >> l >> r;
			if(l > r) swap(l, r);
			cout << tr.query(1, l, r).mx << endl;
		}
		else{
			cin >> p >> s;
			tr.modify(1, p, s);
		}
	}

    return 0;
}

P5522 [yLOI2019] 棠梨煎雪

线段树、压位状态压缩。

题意

歌词中的主人公与她的朋友一年会有一次互相写信给对方，一共通信了 \(m\) 年。为了简化问题，我们认为她们每封信的内容都是一条二进制码，并且所有二进制码的长度都是 \(n\)。即每封信的内容都是一个长度为 \(n\) 的字符串，这个字符串只含字符 0 或 1。

这天她拿出了朋友写给她的所有信件，其中第 \(i\) 年的写的信件编号为 \(i\)。由于信件保存时间过久，上面有一些字符已经模糊不清，我们将这样的位置记为 ?，? 字符可以被解释为 0 或 1。由于她的朋友也是人，符合人类的本质，所以朋友在一段连续的时间中书写的内容可能是相同的。现在她想问问你，对于一段连续的年份区间 \([l,r]\) 中的所有信件，假如朋友在这段时间展示了人类的本质，所写的是同一句话，那么这一句话一共有多少种可能的组成。也即一共有多少字符串 \(S\)，满足在这个区间内的所有信件的内容都可能是 \(S\)。

一个长度为 \(n\) 的只含 0,1,? 的字符串 \(A\) 可能是一个字符串 \(B\) 当且仅当 \(B\) 满足如下条件：

• \(B\) 的长度也是 \(n\) 。
• \(B\) 中只含字符 0,1。
• \(A\) 中所有为 0 的位置在 \(B\) 中也是 0。
• \(A\) 中所有为 1 的位置在 \(B\) 中也是 1。
• \(A\) 中为 ? 的位置在 \(B\) 中可以为 0 也可以是 1。

同时她可能会突然发现看错了某年的信的内容，于是她可能会把某一年的信的内容修改为一个别的只含 0,1,? 的长度为 \(n\) 的字符串。

输入数据第一行为三个用空格隔开的整数，分别代表代表字符串长度 \(n\)，字符串个数 \(m\) 和操作次数 \(q\)。

下面 \(m\) 行，每行是一个长度为 \(n\) 的字符串，第 \((i + 1)\) 行的字符串 \(s_i\) 代表第 \(i\) 年信的内容。

下面 \(q\) 行，每行的第一个数字是操作编号 \(opt\)。

• 如果 \(opt=0\)，那么后面接两个整数 \([l,~r]\)，代表一次查询操作。
• 如果 \(opt=1\)，那么后面接一个整数 \(pos\)，在一个空格后会有一个长度为 \(n\) 的字符串 \(t\)，代表将第 \(pos\) 个字符串修改为新的字符串 \(t\)。

为了避免输出过大，请你输出一行一个数代表所有查询的答案异或和对 \(0\) 取异或的结果。

数据范围

本题采用多测试点捆绑测试，共有 7 个子任务。

子任务编号	$m = $	$q = $	$n = $	子任务分数
\(1\)	\(1\)	\(0\)	\(1\)	\(5\)
\(2\)	\(102\)	\(102\)	\(10\)	\(10\)
\(3\)	\(1003\)	\(1003\)	\(10\)	\(15\)
\(4\)	\(1004\)	\(10004\)	\(30\)	\(15\)
\(5\)	\(100005\)	\(500005\)	\(1\)	\(15\)
\(6\)	\(100006\)	\(50006\)	\(30\)	\(10\)
\(7\)	\(100007\)	\(1000007\)	\(30\)	\(30\)

对于全部的测试点，保证：

• \(1 \leq m \leq 10^5 + 7\)，\(0 \leq q \leq 10^6 + 7\)，\(1 \leq n \leq 30\)。
• \(0 \leq opt \leq 1\)，\(1 \leq pos \leq m\)，\(1 \leq l \leq r \leq m\)。
• \(s_i, t\) 的长度均为 \(n\) 且只含有字符 0,1,?。
• 输入字符串的总长度不超过 \(5 \times 10^6\)。数据在 Linux 下生成，即换行符不含 \r。

---

思路

• 建立线段树，每个叶子节点代表一个字符串。节点内维护两个信息 s0,s1
• s0,s1 分别对字符串 str[i] 的某一位进行状态压缩，如果 str[i]=='?' 则对 s0,s1 |= 1<<i。
• 信息合并时，左右叶子节点异或即可。最后查询看该位如果 s0=s1=1 则答案 *=2，如果 s0=s1=0 答案置 0，其他情况不变。

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/
const int N = 1e5 + 10;
int n, m, q;
string s[N];

// #define _DEBUG

struct SegTree{
    #define ls u << 1
    #define rs u << 1 | 1
    const static int maxn = N;
    struct T{
        int l, r;
        ll s0, s1;
        void operator += (const T& t) {
            s0 &= t.s0;
            s1 &= t.s1;
        }
        void init(int v) {
            if (!v)
                s0 = s1 = 0;
            else 
                s0 = s1 = (1 << n) - 1;
        }
    }tr[maxn << 2];
    void pushup(int u){
        tr[u].s0 = tr[ls].s0 & tr[rs].s0;
        tr[u].s1 = tr[ls].s1 & tr[rs].s1;
    }
    void build(int u, int l, int r){        // 建立线段树，(节点编号，节点区间左端点，节点区间右端点)
        tr[u].l = l, tr[u].r = r;
        if(l == r){
            for (int i = 0; i < n; i++) {
                if (s[l][i] == '?')
                    tr[u].s0 |= 1 << i, tr[u].s1 |= 1 << i;
                else if (s[l][i] == '1') tr[u].s1 |= 1 << i;
                else tr[u].s0 |= 1 << i;
            }
            return;
        }
        int mid = (l + r) >> 1;
        build(ls, l, mid), build(rs, mid + 1, r);       
        pushup(u);
    }   
    T query(int u, int l, int r){
        if(tr[u].l >= l && tr[u].r <= r){
            return tr[u];
        }  
        else{
            int mid = (tr[u].l + tr[u].r) >> 1;
            T res;
            res.init(1);
            if(l <= mid) res = query(ls, l, r);
            if(r > mid) res += query(rs, l, r);
            return res;
        }
    }
    void modify(int u, int pos, string t){         // 单点修改, (节点编号，查询点下标，更改值)
        if(tr[u].l == pos && tr[u].r == pos){   
            tr[u].init(0);
            for (int i = 0; i < n; i++) {
                if (t[i] == '?')
                    tr[u].s0 |= 1 << i, tr[u].s1 |= 1 << i;
                else if (t[i] == '1') tr[u].s1 |= 1 << i;
                else tr[u].s0 |= 1 << i;
            }
            return ;
        } 
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(pos <= mid) modify(ls, pos, t);     
        else modify(rs, pos, t);               
        pushup(u);          // 子节点变化，pushup往父节点更新信息
    }   
}tr;

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> m >> q;
    for (int i = 1; i <= m; i++)
        cin >> s[i];
    tr.build(1, 1, m);
    ll ans = 0;
    while (q--) {
        int op, l, r, pos;
        string str;
        cin >> op;
        #ifdef _DEBUG
        for (int i = 1; i <= m; i++) {
            auto res = tr.query(1, i, i);
            cout << i << ":" << res.s0 << " " << res.s1;
            cout << endl; 
        }
        #endif
        if (op == 0) {
            cin >> l >> r;
            auto res = tr.query(1, l, r);
            ll t = 1;
            for (int i = 0; i < n && t; i++) {
                if (res.s0 >> i & 1 && res.s1 >> i & 1) t <<= 1ll;
                else if (!(res.s0 >> i & 1) && !(res.s1 >> i & 1)) t = 0;
            }
            // cout << "t:" << t << endl;
            ans ^= t;
        }
        else {
            cin >> pos >> str;
            tr.modify(1, pos, str);
        }
    }
    cout << ans << endl;
    return 0;
}

P5677 [GZOI2017]配对统计

树状数组、扫描线、STL

题意

给定 \(n\) 个数 \(a_1,\cdots,a_n\)。

对于一组配对 \((x,y)\)，若对于所有的 \(i=1,2,\cdots,n\)，满足 \(|a_x-a_y|\le|a_x-a_i|(i\not=x)\)，则称 \((x,y)\) 为一组好的配对（\(|x|\) 表示 \(x\) 的绝对值）。

给出若干询问，每次询问区间 \([l,r]\) 中含有多少组好的配对。

即，取 \(x,y\)（\(l\le x,y\le r\) 且 \(x\not=y\)），问有多少组 \((x,y)\) 是好的配对。

第一行两个正整数 \(n,m\)。

第二行 \(n\) 个数 \(a_1,\cdots,a_n\)。

接下来 \(m\) 行，每行给出两个数 \(l,r\)。

\(Ans_i\) 表示第 \(i\) 次询问的答案，输出 \(\sum_{i=1}^m\limits Ans_i\times i\) 即可。

数据范围

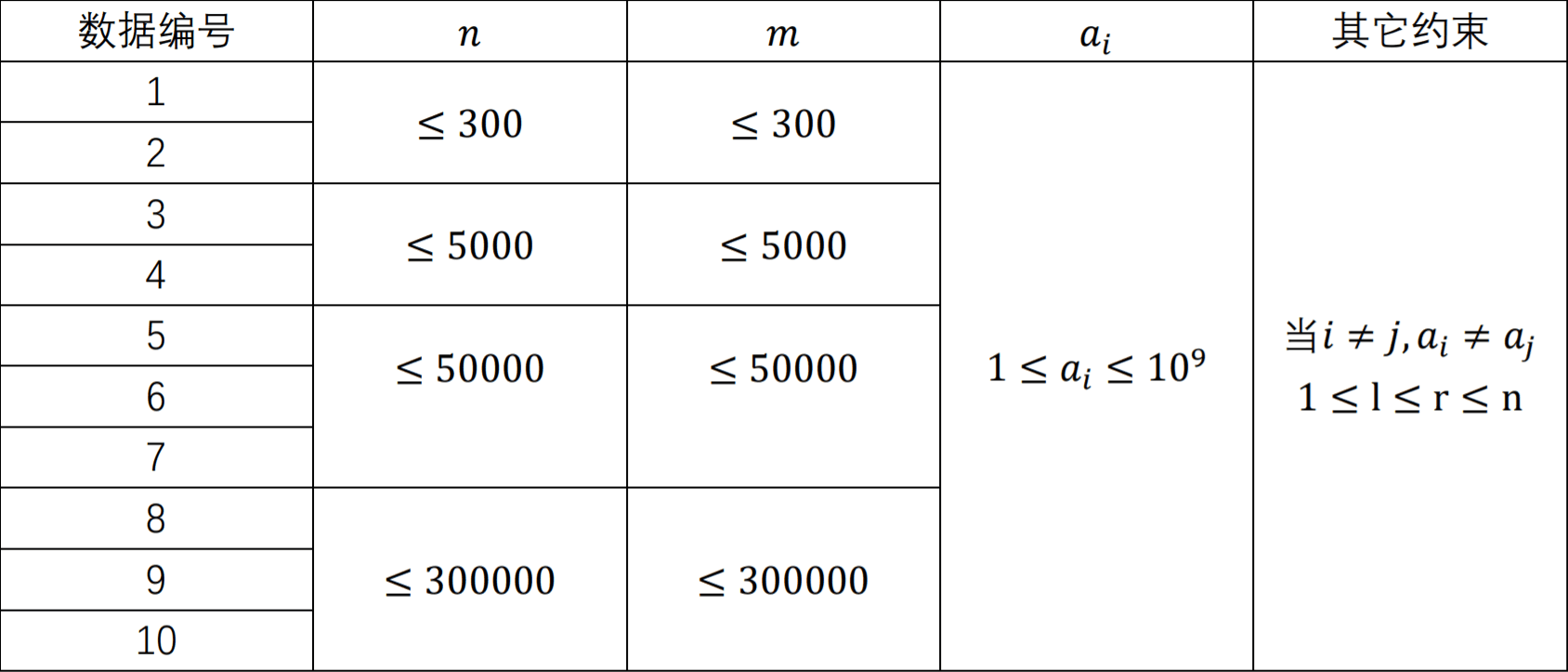
思路

• 配对的含义就是找到每个点距离他绝对值最近的点。可以用 set 存 pair 来实现。
• 拿到了所有的配对，考虑如何统计答案。
• 针对每个询问 [l, r] 如果我们按照 \(r\) 从小到大排序，考虑数组 ans[i] 表示 [i,r] 的配对数量 每次处理一批相同的 \(r\) ，r++ 会有新的配对 [x,y] 进来，会对 ans[x, r] 的区间进行增加，可以用树状数组维护差分实现。然后就做完了，其实就是个扫描线。
• 时间复杂度 \(O(n * logn)\)

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/
const int N = 3e5 + 10, INF = 2e9 + 10;
int n, m, a[N];

template<class T>
struct BIT {
    const static int maxn = 3e5 + 10;
	int n;
	T B[maxn];
	inline int lowbit(int x) { return x & (-x); }
    void init(int _n) {
        n = _n;
    }
	void add(int x, int v) {
		for (int i = x; i <= n; i += lowbit(i)) B[i] += v;
	}
	T ask(int x) {
		T res = 0;
		for (int i = x; i; i -= lowbit(i)) res += B[i];
		return res;
	}
};
BIT<int> bt;

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> m;
    set<PII> S;
    S.insert({INF, -1}), S.insert({-INF, -1});
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        S.insert({a[i], i});
    }
    vector<ll> ans(m + 1, 0);
    vector<vector<array<int,2 >>> ask(n + 1);
    for (int i = 1; i <= m; i++) {
        int l, r;
        cin >> l >> r;
        ask[r].pb({l, i});
    }
    vector<vector<int>> match(n + 1);
    bt.init(n + 1);

    for (int i = 1; i <= n; i++) {
        int x = i;
        S.erase({a[i], i});
        auto it = S.lower_bound({a[i], i});
        auto up = *it;
        auto low = *prev(it);
        int y = -1;
        S.insert({a[i], i});
        if (abs(up.fi - a[i]) < abs(low.fi - a[i])) {
            if (up.se == -1) continue;
            y = up.se;
            if (x > y) swap(x, y);
            match[y].pb(x);
        }
        else if (abs(up.fi - a[i]) > abs(low.fi - a[i])) {
            if (low.se == -1) continue;
            y = low.se;
            if (x > y) swap(x, y);
            match[y].pb(x);
        }
        else {
            match[max(up.se, x)].pb(min(up.se, x));
            match[max(low.se, x)].pb(min(low.se, x));
        }
    }
    for (int r = 1; r <= n; r++) {
        for (auto l: match[r]) 
            bt.add(l, 1);
        for (auto & t: ask[r])  
            ans[t[1]] = bt.ask(r) - bt.ask(t[0] - 1);
    }
    ll res = 0;
    for (int i = 1; i <= m; i++)
        res = res + 1ll * i * ans[i];
    cout << res << endl;
    return 0;
}

\(\color{#83C}{省选+/NOI-}\)

P1505 [国家集训队]旅游

树链剖分、边权转点权、细节

题意

给定一棵 \(n\) 个节点的树，边带权，编号 \(0 \sim n-1\)，需要支持五种操作：

• C i w 将输入的第 \(i\) 条边权值改为 \(w\)
• N u v 将 \(u,v\) 节点之间的边权都变为相反数
• SUM u v 询问 \(u,v\) 节点之间边权和
• MAX u v 询问 \(u,v\) 节点之间边权最大值
• MIN u v 询问 \(u,v\) 节点之间边权最小值

保证任意时刻所有边的权值都在 \([-1000,1000]\) 内。

第一行一个正整数 \(n\)，表示节点个数。
接下来 \(n-1\) 行，每行三个整数 \(u,v,w\)，表示 \(u,v\) 之间有一条权值为 \(w\) 的边，描述这棵树。
然后一行一个正整数 \(m\)，表示操作数。
接下来 \(m\) 行，每行表示一个操作。

对于每一个询问操作，输出一行一个整数表示答案。

数据范围

对于 \(100\%\) 的数据，\(1\le n,m \le 2\times 10^5\)。

思路

• 毫无疑问，先将边权转点权，转移到深度更深的点，并做记录因为要对某个边权进行操作，实际是在点上的。
• 由于是在点对路径上进行的操作，所以想到树链剖分。
• C 操作是很简单的单点修改。
• N 操作是区间取反打个标记，最值交换后取反。
• SUM、MAX、MIN 大同小异。
• 细节：因为边权都转到了深度更小的一方，所以在更新时需要注意一点。
  • 树剖跳出 while (top[u]!=top[v]) 的时候深度更小的一点为两点的LCA，如果两点不同，对边的操作转移到点上实际是 (dfn[u]+1,dfn[v]) +1 是因为两点在同一条重链上，dfs 序连续。
  • 否则就是对单点进行操作。然后忘记给 dfs 里更新深度 debug 1小时 23333.
• 时间复杂度 \(O(nlog^2n)\)

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define get_sz(v) (int)v.size()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
// #define dbg
using namespace std;
/*----------------------------------------------------------------------------------------------------*/
const int N = 2e5 + 10, INF = 1e9;
int n, m, tot;
int sz[N], dfn[N], dep[N], fa[N], rk[N], top[N], hson[N], a[N], id[N];
vector<array<int, 3>> edge[N];
// 边权转点权，点下标+1
// BUG: dfs 忘加深度了。
struct SGT {
    #define ls u << 1
    #define rs u << 1 | 1
    struct T {
        int l, r;
        int w, mx, min_;
        bool fl;
        void init() {
            w = 0, mx = -INF, min_ = INF;
        }
        void operator += (const T& o) {
            mx = max(mx, o.mx), min_ = min(min_, o.min_);
            w = w + o.w;
        }
    }tr[N << 2];
    void pushup(int u) {
        tr[u].mx = max(tr[ls].mx, tr[rs].mx);
        tr[u].min_ = min(tr[ls].min_, tr[rs].min_);
        tr[u].w = tr[ls].w + tr[rs].w;
    }
    void update(T& rt) {
        rt.fl ^= 1;
        rt.w = -rt.w, swap(rt.mx, rt.min_);
        rt.mx = -rt.mx, rt.min_ = -rt.min_;
    }
    void pushdown(int u) {
        if (tr[u].fl) {
            update(tr[ls]), update(tr[rs]);
            tr[u].fl = 0;
        }
    }
    void build(int u, int l, int r) {
        tr[u].l = l, tr[u].r = r;
        if (l == r) {
            tr[u].w = tr[u].mx = tr[u].min_ = a[rk[l]];
            return ;
        }
        int mid = (tr[u].l + tr[u].r) >> 1;
        build(ls, l, mid), build(rs, mid + 1, r);
        pushup(u);
    }
    void modify(int u, int pos, int v) {
        if (tr[u].l == pos && tr[u].r == pos) {
            tr[u].w = tr[u].mx = tr[u].min_ = v;
            return;
        }
        pushdown(u);
        int mid = (tr[u].l + tr[u].r) >> 1;
        if (pos <= mid) modify(ls, pos, v);
        else modify(rs, pos, v);
        pushup(u);
    }
    void modify_range(int u, int l, int r) {
        if (tr[u].l >= l && tr[u].r <= r) {
            update(tr[u]);
            return;
        }
        int mid = (tr[u].l + tr[u].r) >> 1;
        pushdown(u);
        if (l <= mid) modify_range(ls, l, r);
        if (r > mid) modify_range(rs, l, r);
        pushup(u);
    }
    T query(int u, int l, int r) {
        if (tr[u].l >= l && tr[u].r <= r) {
            return tr[u];
        }
        pushdown(u);
        int mid = (tr[u].l + tr[u].r) >> 1;
        T res;
        res.init();
        if (l <= mid) res += query(ls, l, r);
        if (r > mid) res += query(rs, l, r);
        return res;
    }
}tr;

void dfs1(int u) {
    sz[u] = 1, hson[u] = -1;
    for (auto [v, w, idx]: edge[u]) {
        if (v == fa[u]) continue;
        fa[v] = u, a[v] = w, dep[v] = dep[u] + 1;;
        id[idx] = v;
        dfs1(v);
        sz[u] += sz[v];
        if (hson[u] == -1 || sz[v] > sz[hson[u]]) hson[u] = v;
    }
}

void dfs2(int u, int tp) {
    top[u] = tp, dfn[u] = ++tot;
    rk[tot] = u;
    if (hson[u] == -1) return;
    dfs2(hson[u], tp);
    for (auto [v, _, __] : edge[u]) {
        if (v == fa[u] || v == hson[u]) continue;
        dfs2(v, v);
    }
}

void path_modify(int u, int v) {
    u++, v++;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u, v);
        tr.modify_range(1, dfn[top[u]], dfn[u]);
        u = fa[top[u]];
    }
    if (dep[u] > dep[v]) swap(u, v);
    if (u != v)
        tr.modify_range(1, dfn[u] + 1, dfn[v]);
}

int path_query(int u, int v, int t) {
    u++, v++;
    SGT::T res;
    res.init();
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u, v);
        res += tr.query(1, dfn[top[u]], dfn[u]);
        u = fa[top[u]];
    }
    if (dep[u] > dep[v]) swap(u, v);
    if (u != v)
        res += tr.query(1, dfn[u] + 1, dfn[v]);
    if (!t) return res.w;
    if (t == 1) return res.mx;
    return res.min_;
}


int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n;
    for (int i = 1; i < n; i++) {
        int u, v, w;
        cin >> u >> v >> w;
        u++, v++;
        edge[u].pb({v, w, i}), edge[v].pb({u, w, i});
    }
    dep[1] = 1;
    dfs1(1);
    dfs2(1, 1);
    tr.build(1, 1, n);
    cin >> m;
    #ifdef dbg
        cout << "dfn: ";
        for (int i = 1; i <= n; i++)
            cout << rk[i] << " ";
        cout << endl;
    #endif
    while (m--) {
        string op;
        int i, w, u, v;
        cin >> op;
        if (op == "C") {
            cin >> i >> w;
            tr.modify(1, dfn[id[i]], w);
        }
        else if (op == "N") {
            cin >> u >> v;
            path_modify(u, v);
        }
        else if (op == "SUM") {
            cin >> u >> v;
            cout << path_query(u, v, 0) << endl;
        }
        else if (op == "MAX") {
            cin >> u >> v;
            cout << path_query(u, v, 1) << endl;
        }
        else {
            cin >> u >> v;
            cout << path_query(u, v, 2) << endl;
        }
        #ifdef dbg
            for (int i = 1; i <= n; i++)
                cout << tr.query(1, i, i).w << " ";
            cout << endl;
        #endif
    }
    return 0;
}

P2572 [SCOI2010] 序列操作

同时维护01序列,区间取反, 区间赋值, 区间1的个数, 区间连续1的个数

题意

lxhgww 最近收到了一个 \(01\) 序列，序列里面包含了 \(n\) 个数，下标从 \(0\) 开始。这些数要么是 \(0\) ，要么是 \(1\) ，现在对于这个序列有五种变换操作和询问操作：

• 0 l r 把 \([l,r]\) 区间内的所有数全变成 \(0\)
• 1 l r 把 \([l,r]\) 区间内的所有数全变成 \(1\)
• 2 l r 把 \([l,r]\) 区间内的所有数全部取反，也就是说把所有的 \(0\) 变成 \(1\)，把所有的 \(1\) 变成 \(0\)
• 3 l r 询问 \([l,r]\) 区间内总共有多少个 \(1\)
• 4 l r 询问 \([l,r]\) 区间内最多有多少个连续的 \(1\)

对于每一种询问操作，lxhgww 都需要给出回答，聪明的程序员们，你们能帮助他吗？

数据范围
\(1\leq n,m \leq 10^5\)

思路

• 需要的懒标记: same, fl, 进行区间赋值, 和区间翻转, 有区间赋值标记时, 区间翻转对赋值标记^=1, 打same标记时, 让 fl = 0
• 维护信息: 由于需要区间取反, 不同于普通连续子序列最大和, 当类似 00110 这样的区间取反后, 如果只维护1的个数, 取反后11001我们并不能知道取反后1的个数
• 所以在普通信息上, 需要多记录 \(0\) 的信息, 具体见代码, 有压行, 不好看可以去luogu看提交记录

Solution

#include<bits/stdc++.h>
#define endl "\n"
using namespace std;
const int N = 1e5 + 10;
int a[N], n, m;

struct SegTree{
    #define ls u << 1
    #define rs u << 1 | 1
    struct T{
        int l, r, same, fl;
        int v[2], lmx[2], rmx[2], mx[2];	// 因为需要对区间取反， 需要存取 0 和 1 的个数， 否则取反后 pushdown 操作中 1 的个数更新不了
        void init(){
        	for(int i = 0; i < 2; i++)
        		lmx[i] = rmx[i] = mx[i] = v[i] = (a[l] == i);
        	fl = 0;
        	same = -1;
        }
        void init(int x){ for(int i = 0; i < 2; i++) l = r = lmx[i] = rmx[i] = mx[i] = v[i] = 0; }
   	};
    vector<T> tr;
    SegTree(int n): tr((n + 1) << 2) {build(1, 1, n);};
    void pushup(T& rt, T& lson, T& rson){
    	int len1 = lson.r - lson.l + 1, len2 = rson.r - rson.l + 1;
    	for(int i = 0; i < 2; i++){
	    	rt.v[i] = lson.v[i] + rson.v[i];
	    	if(lson.v[i] == len1) rt.lmx[i] = len1 + rson.lmx[i];
	    	else rt.lmx[i] = lson.lmx[i];
	    	if(rson.v[i] == len2) rt.rmx[i] = len2 + lson.rmx[i];
	    	else rt.rmx[i] = rson.rmx[i];
	    	rt.mx[i] = max(max(lson.mx[i], rson.mx[i]), lson.rmx[i] + rson.lmx[i]);
    	}
    }
    void pushup(int u){ pushup(tr[u], tr[ls], tr[rs]); }
    void update_same(T& rt, int same){
    	for(int i = 0; i < 2; i++)		// 标记用于更新子节点， 当前节点的值必须在update里更新为最准确的值
	    	rt.lmx[i] = rt.rmx[i] = rt.mx[i] = rt.v[i] = (same == i) * (rt.r - rt.l + 1);
    	rt.same = same;
    	rt.fl = 0;
    }
    void update_fl(T& rt){
    	swap(rt.lmx[0], rt.lmx[1]);
    	swap(rt.rmx[0], rt.rmx[1]);
    	swap(rt.mx[0], rt.mx[1]);
    	swap(rt.v[0], rt.v[1]);
    	if(rt.same != -1) rt.same ^= 1;
    	else rt.fl ^= 1;
    }
    void pushdown(int u){
    	if(tr[u].same != -1){
    		int same = tr[u].same;
    		update_same(tr[ls], same);
    		update_same(tr[rs], same);
    		tr[u].same = -1;
    	}
    	else if(tr[u].fl){
    		update_fl(tr[ls]);
    		update_fl(tr[rs]);
    		tr[u].fl = 0;
    	}
    }
    void build(int u, int l, int r){        // 建立线段树，(节点编号，节点区间左端点，节点区间右端点)
        tr[u] = (T){l, r, -1, 0}; 
        if(l == r){ tr[u].init(); return; }
        int mid = (l + r) >> 1;
        build(ls, l, mid), build(rs, mid + 1, r);       
        pushup(u);
    }   
    T query(int u, int l, int r){
    	if(tr[u].l > r || tr[u].r < l) return {0,0,0,0,0};
        if(tr[u].l >= l && tr[u].r <= r) return tr[u];
        else{
            pushdown(u);        // 递归分裂前pushdown
            int mid = (tr[u].l + tr[u].r) >> 1;
            T lt, rt, res;
            lt.init(0), rt.init(0);
            if (l <= mid) lt = query(ls, l, r);
            if (r > mid) rt = query(rs, l, r);
            pushup(res, lt, rt);
            return res;
        }
    }
    void modify(int u, int l, int r, int v, int t){    // 区间修改
    	if(tr[u].l > r || tr[u].r < l) return;
        if(tr[u].l >= l && tr[u].r <= r){       // 注意区间修改的递归出口
        	if(t) update_fl(tr[u]);
        	else update_same(tr[u], v);
            return ;
        }
        pushdown(u);        // 递归分裂前 pushdown  
        int mid = (tr[u].l + tr[u].r) >> 1;
        if(l <= mid) modify(ls, l, r, v, t);
        if(r > mid) modify(rs, l, r, v, t);
        pushup(u);
    }
};

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n >> m;
	for (int i = 1; i <= n; i++) cin >> a[i];
	SegTree tr(n);
	while (m--) {
		int op, l, r;
		cin >> op >> l >> r, l++, r++;
		if (op < 3) tr.modify(1, l, r, op, op == 2);
		else { auto res = tr.query(1, l, r); cout << (op == 3 ? res.v[1] : res.mx[1]) << endl; }
	}
    return 0;
}

P2633 Count on a tree

可持久化01Trie/主席树、树上差分、根到点路径信息维护、LCA

题意

给定一棵 \(n\) 个节点的树，每个点有一个权值。有 \(m\) 个询问，每次给你 \(u,v,k\)，你需要回答 \(u \text{ xor last}\) 和 \(v\) 这两个节点间第 \(k\) 小的点权。

其中 \(\text{last}\) 是上一个询问的答案，定义其初始为 \(0\)，即第一个询问的 \(u\) 是明文。

第一行两个整数 \(n,m\)。

第二行有 \(n\) 个整数，其中第 \(i\) 个整数表示点 \(i\) 的权值。

后面 \(n-1\) 行每行两个整数 \(x,y\)，表示点 \(x\) 到点 \(y\) 有一条边。

最后 \(m\) 行每行两个整数 \(u,v,k\)，表示一组询问。

\(m\) 行，每行一个正整数表示每个询问的答案。

数据范围
对于 \(100\%\) 的数据，\(1\le n,m \le 10^5\)。

思路

• 主席树或者可持久化01Trie都可以完成本题。
• 数据结构维护的信息是根到节点的路径的值域空间。
• 查找两点间第 \(k\) 小用到树上差分的思想，因此还需要用到 LCA
  \[sz[u]+sz[v]-sz[lca(u,v]-sz[fa[lca(u,v)]] \]

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

const int N = 1e5 + 10, Lg = 20, M = 30;
int dep[N], fa[N][Lg], n, m, a[N];
int h[N], e[N << 1], ne[N << 1], idx_;

void add(int a, int b) {
    e[idx_] = b, ne[idx_] = h[a], h[a] = idx_++;
}

int lca(int a, int b);

struct Presistent_01Trie {
    int node_cnt, root[N];
    struct Node {
        int ch[2], sz;
    }tr[N * M * 2];
    int get_node() {
        node_cnt ++;
        tr[node_cnt].ch[0] = tr[node_cnt].ch[1] = 0;
        tr[node_cnt].sz = 0;
        return node_cnt;
    }
    void update(Node& rt) {
        rt.sz = tr[rt.ch[0]].sz + tr[rt.ch[1]].sz;
    }
    void insert(int x, int p, int q, int base) {    // p 旧根， q 新根
        if (base == -1) {
            tr[q].sz ++;
            return;
        }
        int u = x >> base & 1;
        if (tr[p].ch[u ^ 1]) tr[q].ch[u ^ 1] = tr[p].ch[u ^ 1];
        tr[q].ch[u] = get_node();
        insert(x, tr[p].ch[u], tr[q].ch[u], base - 1);
        update(tr[q]);
    }
    ll query_kth(int k, int u, int v) {
        int lca_uv = lca(u, v), lca_fa = fa[lca_uv][0];
        u = root[u], v = root[v], lca_uv = root[lca_uv], lca_fa = root[lca_fa];
        ll res = 0;
        for (int i = M; ~i; i--) {
            int lsz = tr[tr[u].ch[0]].sz + tr[tr[v].ch[0]].sz - tr[tr[lca_uv].ch[0]].sz - tr[tr[lca_fa].ch[0]].sz;
            if (lsz >= k) 
                u = tr[u].ch[0], v = tr[v].ch[0], lca_uv = tr[lca_uv].ch[0], lca_fa = tr[lca_fa].ch[0];
            else {
                res |= 1ll << i;
                u = tr[u].ch[1], v = tr[v].ch[1], lca_uv = tr[lca_uv].ch[1], lca_fa = tr[lca_fa].ch[1];
                k -= lsz;
            }
        }
        return res;
    }
}Tr;

int lca(int a, int b) {              // 求点 a 和 点 b 的最近公共祖先
    if(dep[a] < dep[b])
        swap(a, b);
    int d = dep[a] - dep[b];                // 深度大的是 a
    for (int i = 0; i < Lg && d; i++, d /= 2) {
        if(d & 1)
            a = fa[a][i];
    }
    if (a == b) return a;
    for (int i = Lg - 1; i >= 0; i--)
        if (fa[a][i] != fa[b][i])
            a = fa[a][i], b = fa[b][i];
    return fa[a][0];
}

void dfs_lca(int u, int p) {
    Tr.root[u] = Tr.get_node();
    Tr.insert(a[u], Tr.root[p], Tr.root[u], M);
    for (int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if (j == p) continue;
        dep[j] = dep[u] + 1;
        fa[j][0] = u;
        dfs_lca(j, u);
    }
}

void init() {
    for (int i = 1; i < Lg; i++)             // 先循环跳的次数
        for (int j = 1; j <= n; j++)             // 再循环节点个数
            if (fa[j][i - 1])
                fa[j][i] = fa[fa[j][i - 1]][i - 1];
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    for (int i = 1; i < n; i++) {
        int x, y;
        cin >> x >> y;
        add(x, y), add(y, x);
    }
    dfs_lca(1, 0);
    init();
    int last = 0;
    while (m--) {
        int u, v, k;
        cin >> u >> v >> k;
        last = Tr.query_kth(k, u ^ last, v);
        cout << last << endl;
    }
    return 0;
}

P3313 [SDOI2014]旅行

动态开点线段树、树链剖分、dfs序

题意

在 \(n\) 个点的树上，在S国的历史上常会发生以下几种事件：

“CC x c“：城市x的居民全体改信了c教；

“CW x w“：城市x的评级调整为w;

“QS x y“：一位旅行者从城市x出发，到城市y，并记下了途中留宿过的城市的评级总和；

“QM x y“：一位旅行者从城市x出发，到城市y，并记下了途中留宿过的城市的评级最大值。

由于年代久远，旅行者记下的数字已经遗失了，但记录开始之前每座城市的信仰与评级，还有事件记录本身是完好的。请根据这些信息，还原旅行者记下的数字。 为了方便，我们认为事件之间的间隔足够长，以致在任意一次旅行中，所有城市的评级和信仰保持不变。

输入的第一行包含整数N，Q依次表示城市数和事件数。

接下来N行，第i+l行两个整数Wi，Ci依次表示记录开始之前，城市i的评级和信仰。 接下来N-1行每行两个整数x，y表示一条双向道路。

接下来Q行，每行一个操作，格式如上所述。

对每个QS和QM事件，输出一行，表示旅行者记下的数字。

数据范围

\(N，Q < =10^5 ， C < =10^5\)

数据保证对所有QS和QM事件，起点和终点城市的信仰相同；在任意时

刻，城市的评级总是不大于10^4的正整数，且宗教值不大于C。

思路

• 涉及四种操作，改单点宗教、评级、链上同宗教评级和、最大值查询
• 如果没有宗教要求很好维护。考虑一种暴力的方式开 \(C\) 个线段树来维护，空间太大？发现题目的加点操作只有 \(O(n)\) 个涉及 \(O(nlogn)\) 个线段树节点，所以我们可以动态开点！，然后这题不是主席树，我觉得很难维护不同宗教的信息。
• 总的来说 dfs序 + 动态开点线段树 + 树链剖分 ！时间复杂度 \(O(nlogn)\)

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define get_sz(v) (int)v.size()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
// #define dbg
using namespace std;
/*----------------------------------------------------------------------------------------------------*/
const int N = 1e5 + 10;
int n, m, tot;
int sz[N], dfn[N], dep[N], fa[N], rk[N], top[N], hson[N];
vector<int> edge[N];
// 在DFS序上建立动态开点线段树 (并不太是主席树，主席树不太好统计宗教类型) + 树剖链上查询

// root[i] 表示宗教为i的线段树根节点。
// CC: just insert


struct Dynamic_Memory_Tree {
    int node_cnt, root[N];
    struct T {
        int l, r;
        int w, mx;
    }tr[N * 40];
    int get_node() {
        node_cnt++;
        tr[node_cnt].l = tr[node_cnt].r = tr[node_cnt].w = 0;
        return node_cnt;
    }
    void pushup(T& rt) {
        rt.mx = max(tr[rt.l].mx, tr[rt.r].mx);
        rt.w = tr[rt.l].w + tr[rt.r].w;
    }
    void insert(int& q, int l, int r, int w, int pos) {
        if (!q) q = get_node();
        if (l == r) {
            tr[q].w = tr[q].mx = w;
            return ;
        }
        int mid = (l + r) >> 1;
        if (pos <= mid) insert(tr[q].l, l, mid, w, pos);
        else insert(tr[q].r, mid + 1, r, w, pos);
        pushup(tr[q]);
        return;
    }
    void modify(int u, int l, int r, int pos, int w) {
        if (l == r) {
            tr[u].w = tr[u].mx = w;
            return ;
        }
        int mid = (l + r) >> 1;
        if (pos <= mid) modify(tr[u].l, l, mid, pos, w);
        else modify(tr[u].r, mid + 1, r, pos, w);
        pushup(tr[u]);
        return;
    }
    int query_max(int u, int l, int r, int ql, int qr) {
        if (l > qr || r < ql) return 0;
        if (ql <= l && r <= qr) {
            return tr[u].mx;
        }
        int mid = (l + r) >> 1, res = 0;
        if (ql <= mid) res = query_max(tr[u].l, l, mid, ql, qr);
        if (qr > mid) res = max(res, query_max(tr[u].r, mid + 1, r, ql, qr));
        return res;
    }
    int query_sum(int u, int l, int r, int ql, int qr) {
        if (l > qr || r < ql) return 0;
        if (ql <= l && r <= qr) {
            return tr[u].w;
        }
        int mid = (l + r) >> 1, res = 0;
        if (ql <= mid) res = query_sum(tr[u].l, l, mid, ql, qr);
        if (qr > mid) res = res + query_sum(tr[u].r, mid + 1, r, ql, qr);
        return res;
    }
}dtr;

struct info {
    int w, c;
}city[N];

void dfs1 (int u) {
    sz[u] = 1, hson[u] = -1;
    for (auto v: edge[u]) {
        if (v == fa[u]) continue;
        fa[v] = u, dep[v] = dep[u] + 1;
        dfs1(v);
        sz[u] += sz[v];
        if (hson[u] == -1 || sz[v] > sz[hson[u]]) hson[u] = v;
    }
}

void dfs2(int u, int tp) {
    top[u] = tp, dfn[u] = ++tot;
    rk[tot] = u;
    if (hson[u] == -1) return;
    dfs2(hson[u], tp);
    for (auto v: edge[u]) {
        if (v == fa[u] || v == hson[u]) continue;
        dfs2(v, v);
    }
}

int path_sum(int u, int v, int c) {
    int res = 0;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u, v);
        #ifdef dbg
            cout << "u:" << u << endl;
            cout << "l r:" << dfn[top[u]]  << " " << dfn[u] << endl;
        #endif
        res += dtr.query_sum(dtr.root[c], 1, n, dfn[top[u]], dfn[u]);
        u = fa[top[u]];
    }
    if (dep[u] > dep[v]) swap(u, v);
    #ifdef dbg
        cout << "u v:" << u << " " << v << endl;
        cout << "check : " << dfn[u] << " " << dfn[v] << " " <<  dtr.query_sum(rt, 1, n, dfn[u], dfn[v]) << endl;
    #endif
    return res + dtr.query_sum(dtr.root[c], 1, n, dfn[u], dfn[v]);
}

int path_max(int u, int v, int c) {
    int res = 0;
    while (top[u] != top[v]) {
        if (dep[top[u]] < dep[top[v]]) swap(u, v);
        res = max(res, dtr.query_max(dtr.root[c], 1, n, dfn[top[u]], dfn[u]));
        u = fa[top[u]];
    }
    if (dep[u] > dep[v]) swap(u, v);
    res = max(res, dtr.query_max(dtr.root[c], 1, n, dfn[u], dfn[v]));
    return res;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> city[i].w >> city[i].c;
    for (int i = 1; i < n; i++) {
        int a, b;
        cin >> a >> b;
        edge[a].pb(b), edge[b].pb(a);
    }
    dep[1] = 1;
    dfs1(1);
    dfs2(1, 1);
    for (int i = 1; i <= n; i++) {
        int u = rk[i];
        dtr.insert(dtr.root[city[u].c], 1, n, city[u].w, i);
    }
    #ifdef dbg
        for (int i = 1; i <= n; i++)
            cout << rk[i] <<  " ";
        cout << endl;
    #endif
    while (m--) {
        string op;
        int x, c, w, y;
        cin >> op;
        if (op == "CC") {
            cin >> x >> c;
            dtr.modify(dtr.root[city[x].c], 1, n, dfn[x], 0);
            dtr.insert(dtr.root[c], 1, n, city[x].w, dfn[x]);
            city[x].c = c;
        }
        else if (op == "CW") {
            cin >> x >> w;
            dtr.modify(dtr.root[city[x].c], 1, n, dfn[x], w);
            city[x].w = w;
        }
        else if (op == "QS") {
            cin >> x >> y;
            // cout << "root:" << city[x].c << endl;
            cout << path_sum(x, y, city[x].c) << endl;
        }
        else {
            cin >> x >> y;
            cout << path_max(x, y, city[x].c) << endl;
        }
        #ifdef dbg
        for (int i = 1; i <= 3; i++) {
            cout << dtr.query_sum(dtr.root[i], 1, n, 1, n) << " ";
        }
        cout << endl;
        #endif
    }
    return 0;
}

P3586 [POI2015] LOG

树状数组、构造

题意

维护一个长度为 \(n\) 的序列，一开始都是 \(0\)，支持以下两种操作：

1. U k a 将序列中第 \(k\) 个数修改为 \(a\)。
2. Z c s 在这个序列上，每次选出 \(c\) 个正数，并将它们都减去 \(1\)，询问能否进行 \(s\) 次操作。

每次询问独立，即每次询问不会对序列进行修改。

第一行包含两个正整数 \(n,m\)，分别表示序列长度和操作次数。

接下来 \(m\) 行为 \(m\) 个操作。

包含若干行，对于每个 Z 询问，若可行，输出 TAK，否则输出 NIE。

数据范围

对于 \(100\%\) 的数据，\(1\leq n,m\leq 10^6\)，\(1\leq k,c\leq n\)，\(0\leq a\leq 10^9\)，\(1\leq s\leq 10^9\)。

思路

• 首先可以知道大于 \(s\) 的正数一定每次都会被用到设个数为 \(cnt\)，然后考虑小于等于 \(s\) 的正数。
• 构造结论：如果小于等于 \(s\) 的正数和 \(sum\geq (c-cnt) * s\)，那么一定能操作成功。
  • 把每一个数看成几层石头，每种石头不超过 \(s\) 层，那么我们把每堆石子往小的方向堆，同一种石子一定是在不同层。
  • 最后如果层数等于 \(s\) 的石头堆数超过 \(c-cnt\) 个就构造成功了。即 \(sum\geq (c-cnt) * s\)
• 最后用树状数组离线维护 每个数的出现次数，权值和。复杂度 \(O(nlogn)\)，不过我的代码好像得开 \(O2\) 不太懂为什么卡最后一点。

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/
template<class T>
struct BIT {
    const static int maxn = 2e6 + 10;
	int n;
	T B[maxn];
	inline int lowbit(int x) { return x & (-x); }
    void init(int _n) {
        n = _n;
    }
	void add(int x, ll v) {
		for (int i = x; i <= n; i += lowbit(i)) B[i] += v;
	}
	T ask(int x) {
		T res = 0;
		for (int i = x; i; i -= lowbit(i)) res += B[i];
		return res;
	}
};
BIT<ll> bt1, bt2;

vector<ll> alls;

struct Q {
    string op;
    int c, s;
};

int find (ll x) {
    return lower_bound(arr(alls), x) - alls.begin() + 1;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    vector<Q> q;
    int n, m;
    cin >> n >> m;
    vector<ll> a(n + 1, 0);
    for (int i = 0; i < m; i++) {
        string op;
        int c, s;
        cin >> op >> c >> s;
        q.pb({op, c, s});
        alls.pb(s);
    }
    sort(arr(alls));
    alls.erase(unique(arr(alls)), alls.end());
    int sz = alls.size();
    sz++;
    bt1.init(sz), bt2.init(sz);
    for (int i = 0; i < m; i++) {
        auto [op, c, s] = q[i];
        if (op == "U") {
            int pos = find(a[c]);
            bt1.add(pos, -1);
            bt2.add(pos, -a[c]);
            a[c] = s;
            pos = find(a[c]);
            bt1.add(pos, 1);
            bt2.add(pos, a[c]);
        }
        else {
            int pos = find(s);
            int cnt = bt1.ask(sz) - bt1.ask(pos);
            if (bt2.ask(pos) >= 1ll * (c - cnt) * s) cout << "TAK\n";
            else cout << "NIE\n";
        }
    }
    return 0;
}

P4592 [TJOI2018]异或

可持久化 01-Trie, 链上问题、子树问题。

题意

现在有一颗以 \(1\) 为根节点的由 \(n\) 个节点组成的树，节点从 \(1\) 至 \(n\) 编号。树上每个节点上都有一个权值 \(v_i\)。现在有 \(q\) 次操作，操作如下：

• \(1~x~z\)：查询节点 \(x\) 的子树中的节点权值与 \(z\) 异或结果的最大值。
• \(2~x~y~z\)：查询节点 \(x\) 到节点 \(y\) 的简单路径上的节点的权值与 \(z\) 异或结果最大值。

输入的第一行是两个整数，分别代表结点个数 \(n\) 和询问个数 \(q\)。

第二行有 \(n\) 个整数，第 \(i\) 个整数表示点 \(i\) 的的权值 \(v_i\)。

接下来 \((n-1)\) 行，每行有两个整数 \(u, v\)，表示存在一条连结 \(u\) 和 \(v\) 的边。

接下来 \(q\) 行，每行首先有一个整数 \(op\)，代表操作类型。

• 若 \(op = 1\)，则一个空格后有两个整数 \(x, z\)，代表查询节点 \(x\) 的子树中的节点权值与 \(z\) 异或结果的最大值。
• 若 \(op = 2\)，则一个空格后有三个整数 \(x, y, z\)，代表查询节点 \(x\) 到节点 \(y\) 的简单路径上的节点的权值与 \(z\) 异或结果最大值。

对于每一个查询，输出一行一个整数代表答案。

数据范围

• 对于 \(10\%\) 的数据，保证 \(n, q \leq 10^2\)。
• 对于 \(20\%\) 的数据，保证 \(n, q \leq 10^3\)。
• 对于 \(40\%\) 的数据，保证 \(n, q \leq 10^4\)。
• 对于 \(100\%\) 的数据，保证 \(1< n, q \leq10^5\)，\(1 \leq u, v, x, y \leq n\)，\(1 \leq op \leq 2\)，\(1 \leq v_i, z \lt 2^{30}\)。

思路

• 对于子树查询，建立在 dfs 序上建立可持久化 01-Trie 即可。
• 对于路径上查询，可以考虑树上差分的做法，也可以考虑改成对两条链上的查询，u 到 lca 和 v 到 lca 的查询取max。需要用可持久化 01Trie 维护根到节点的信息，因为具有区间可减性。

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

const int N = 2e5 + 10, Lg = 21, M = 30;
int dep[N], fa[N][Lg], n, m, dfn[N], in[N], out[N], tot;
int h[N], e[N << 1], ne[N << 1], idx_;
ll a[N];

void add(int a, int b) {
    e[idx_] = b, ne[idx_] = h[a], h[a] = idx_++;
}

int lca(int a, int b);

struct Presistent_01Trie {
    ll node_cnt, root[N];
    struct Node {
        int ch[2], sz;
    }tr[N * M * 2];
    ll get_node() {
        node_cnt ++;
        tr[node_cnt].ch[0] = tr[node_cnt].ch[1] = 0;
        tr[node_cnt].sz = 0;
        return node_cnt;
    }
    void update(Node& rt) {
        rt.sz = tr[rt.ch[0]].sz + tr[rt.ch[1]].sz;
    }
    void insert(int x, int p, int q) {
        for (int i = M; ~i; i--) {
            int u = x >> i & 1;
            tr[q].ch[!u] = tr[p].ch[!u];
            tr[q].ch[u] = get_node();
            q = tr[q].ch[u], p = tr[p].ch[u];
            tr[q].sz = tr[p].sz + 1;
        }
    }
    ll query(int p, int q, int x) {
        ll res = 0;
        for (int i = M; ~i; i--) {
            int u = x >> i & 1;
            if (tr[tr[q].ch[u ^ 1]].sz > tr[tr[p].ch[u ^ 1]].sz) {
                p = tr[p].ch[u ^ 1], q = tr[q].ch[u ^ 1];
                res |= 1ll << i;
            }
            else p = tr[p].ch[u], q = tr[q].ch[u];
        }
        return res;
    }
}tree1, tree2;

int lca(int a, int b) {              // 求点 a 和 点 b 的最近公共祖先
    if(dep[a] < dep[b])
        swap(a, b);
    int d = dep[a] - dep[b];                // 深度大的是 a
    for (int i = 0; i < Lg && d; i++, d /= 2) {
        if(d & 1)
            a = fa[a][i];
    }
    if (a == b) return a;
    for (int i = Lg - 1; i >= 0; i--)
        if (fa[a][i] != fa[b][i])
            a = fa[a][i], b = fa[b][i];
    return fa[a][0];
}

void dfs_lca(int u, int p) {
    tree2.root[u] = tree2.get_node();
    tree2.insert(a[u], tree2.root[p], tree2.root[u]);
    dfn[++tot] = u;
    in[u] = tot;
    for (int i = h[u]; ~i; i = ne[i]){
        int j = e[i];
        if (j == p) continue;
        dep[j] = dep[u] + 1;
        fa[j][0] = u;
        dfs_lca(j, u);
    }
    out[u] = tot;
}

void init() {
    for (int i = 1; i < Lg; i++)             // 先循环跳的次数
        for (int j = 1; j <= n; j++)             // 再循环节点个数
            if (fa[j][i - 1])
                fa[j][i] = fa[fa[j][i - 1]][i - 1];
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    for (int i = 1; i < n; i++) {
        int x, y;
        cin >> x >> y;
        add(x, y), add(y, x);
    }
    dfs_lca(1, 0);
    init();
    for (int i = 1; i <= n; i++) {
        tree1.root[i] = tree1.get_node();
        tree1.insert(a[dfn[i]], tree1.root[i - 1], tree1.root[i]);
    }
    while (m--) {
        int op, x, y, z;
        cin >> op >> x >> y;
        if (op == 1) {
            int l = in[x], r = out[x];
            cout << tree1.query(tree1.root[l - 1], tree1.root[r], y) << endl;
        }
        else {
            cin >> z;
            int u = lca(x, y);
            cout << max(tree2.query(tree2.root[fa[u][0]], tree2.root[y], z), tree2.query(tree2.root[fa[u][0]], tree2.root[x], z)) << endl;
        }
    }
    return 0;
}

P4735 最大异或和

可持久化 01-Trie，前缀和，模板

题意

给定一个非负整数序列 \(\{a\}\)，初始长度为\(n\)。

有 \(m\) 个操作，有以下两种操作类型：

1. A x：添加操作，表示在序列末尾添加一个数 \(x\)，序列的长度 \(n+1\)。
2. Q l r x：询问操作，你需要找到一个位置 \(p\)，满足\(l \le p \le r\)，使得： $
   a[p] \oplus a[p+1] \oplus ... \oplus a[N] \oplus x$ 最大，输出最大是多少。

第一行包含两个整数 \(N,M\)，含义如问题描述所示。
第二行包含 \(N\)个非负整数，表示初始的序列$ A$ 。
接下来 \(M\)行，每行描述一个操作，格式如题面所述。

假设询问操作有 \(T\) 个，则输出应该有 \(T\) 行，每行一个整数表示询问的答案。

数据范围

对于测试点 \(1-2\)，\(N,M \le 5\)。
对于测试点 \(3-7\)，\(N,M \le 80000\)。
对于测试点 \(8-10\)，\(N,M \le 300000\)。
其中测试点 \(1, 3, 5, 7, 9\)保证没有修改操作。
\(0 \le a[i] \le 10^7\)。

思路

• 通过前缀和转化为 s[n] ^ x ^ s[p], l-1 <= p <= r-1 的异或最大问题。
• 然后建立可持久化 01trie 解决即可。

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

/*可持久化01-Trie 在 [l-1, r-1] 中找最大异或对*/

const int N = 5e5 + 10, M = 24;
int n, m, a[N], root[N];
int son[N * M][2], idx;        // idx存放节点编号， 0号节点既是根也是空节点
int mx_id[N * M * 2];         

void insert(int id, int p, int q) {    // 插入
    for (int i = M; ~i; i--) {
        int u = a[id] >> i & 1;
        if (p) son[q][u ^ 1] = son[p][u ^ 1];
        son[q][u] = ++idx;
        p = son[p][u], q = son[q][u];
        mx_id[q] = id;
    }
    // cnt[p] ++;  // 对末尾节点做标记
}

int query(int p, int l, int x) {
    for (int i = M; ~i; i --) {
        int u = x >> i & 1;
        if (mx_id[son[p][u ^ 1]] >= l) p = son[p][u ^ 1];
        else p = son[p][u];
    }
    return a[mx_id[p]];
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> m;
    root[0] = ++idx;
    mx_id[0] = -1;      // 取最小
    insert(0, 0, root[0]);
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        a[i] ^= a[i - 1];
        root[i] = ++idx;
        insert(i, root[i - 1], root[i]);
    }
    while (m--) {
        string op;
        int l, r, x;
        cin >> op;
        if (op == "A") {
            cin >> x;
            a[++n] = x;
            root[n] = ++idx;
            a[n] ^= a[n - 1];
            insert(n, root[n - 1], root[n]);
        }
        else {
            cin >> l >> r >> x;
            cout << (x ^ a[n] ^ query(root[r - 1], l - 1, x ^ a[n])) << endl;
        }
    }
    return 0;
}

P5283 [十二省联考 2019] 异或粽子

01-Trie, 第 \(k\) 大问题

题意

小粽面前有 \(n\) 种互不相同的粽子馅儿，小粽将它们摆放为了一排，并从左至右编号为 \(1\) 到 \(n\)。第 \(i\) 种馅儿具有一个非负整数的属性值 \(a_i\)。每种馅儿的数量都足够多，即小粽不会因为缺少原料而做不出想要的粽子。小粽准备用这些馅儿来做出 \(k\) 个粽子。

小粽的做法是：选两个整数数 \(l\), \(r\)，满足 \(1 \leqslant l \leqslant r \leqslant n\)，将编号在 \([l, r]\) 范围内的所有馅儿混合做成一个粽子，所得的粽子的美味度为这些粽子的属性值的异或和。（异或就是我们常说的 xor 运算，即 C/C++ 中的 ˆ 运算符或 Pascal 中的 xor 运算符）

小粽想品尝不同口味的粽子，因此它不希望用同样的馅儿的集合做出一个以上的
粽子。

小粽希望她做出的所有粽子的美味度之和最大。请你帮她求出这个值吧！

第一行两个正整数 \(n\), \(k\)，表示馅儿的数量，以及小粽打算做出的粽子的数量。

接下来一行为 \(n\) 个非负整数，第 \(i\) 个数为 \(a_i\)，表示第 \(i\) 个粽子的属性值。
对于所有的输入数据都满足：\(1 \leqslant n \leqslant 5 \times 10^5\), \(1 \leqslant k \leqslant \min\left\{\frac{n(n-1)}{2},2 \times 10^{5}\right\}\), \(0 \leqslant a_i \leqslant 4 294 967 295\)。

输出一行一个整数，表示小粽可以做出的粽子的美味度之和的最大值。

数据范围

测试点	\(n\)	\(k\)
\(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\)	\(\leqslant 10^3\)	\(\leqslant 10^3\)
\(9\), \(10\), \(11\), \(12\)	\(\leqslant 5 \times 10^5\)	\(\leqslant 10^3\)
\(13\), \(14\), \(15\), \(16\)	\(\leqslant 10^3\)	\(\leqslant 2 \times 10^5\)
\(17\), \(18\), \(19\), \(20\)	\(\leqslant 5 \times 10^5\)	\(\leqslant 2 \times 10^5\)

思路

• 容易想到利用异或前缀和搭配 01-Trie 来解决异或最大问题，那么如何解决前 \(k\) 大呢？
• 毫无疑问需要使用大根堆来解决，对于单值来说找到第 \(k\) 大比较简单，记录各节点的子树标记个数，依次往下走即可。
• 解决方案：先将 \(n +1\) 个前缀异或和放进堆里，记录对应下标、对应已经查找了前 \(t\) 大的数，然后依次取出 \(k\) 个最大值即可，事实上，我们需要取出 \(2 * k\) 个最大值，因为有一份冗余。
• 来个简单的证明：
  • 最后前 \(k\) 大设 \(x\) 下标有 \(n\)个， \(y\) 下标有 \(m\) 个。两个下标不同值之间的顺序一定是正确的。
  • 设 \(x_1 > y_1\), \(x_2 < y_2\) ，优先队列中的顺序： \(x_1>y_1...y_2>x_2\)，\(x_1\) 一定比 \(y_1\) 先出队列。也意味着 \(x_2\) 也先进入队列，但由于 \(x_2<y_2<y_1\) ，\(x_2\) 一定比 \(y_1,y_2\) 晚出队列。
  • 将情况扩展到 \(n+1\) 个下标，正确性依然成立，所以这样取是能找到前 \(k\) 大的。
• 时间复杂度 \(O(32*n + k*logk)\)

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/
const int N = 5e5 + 10, M = 31;
ll n, k, a[N], s[N];
int son[N * 32][2], idx, sz[N * 2 * 32];        // idx存放节点编号， 0号节点既是根也是空节点

void insert(ll x) {    // 插入
    int p = 0;
    for (int i = M; ~i; i--) {
        ll u = x >> i & 1;
        if (!son[p][u]) son[p][u] = ++idx;
        p = son[p][u];
        sz[p] ++;
    }
}

ll query(ll x, int t) {
    int p = 0;
    ll res = 0;
    for (int i = M; ~i; i--) {
        ll u = x >> i & 1;
        if (sz[son[p][u ^ 1]] >= t) {
            res |= 1ll << i;
            p = son[p][u ^ 1];
        }
        else {
            t -= sz[son[p][u ^ 1]];
            p = son[p][u];
        } 
    }
    return res;
}

struct Node {
    ll val, t, id;
    bool operator < (const Node & o) const {
        return val < o.val;
    }
};

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> n >> k;
    for (int i = 1; i <= n; i++)
        cin >> a[i];
    insert(0);
    for (int i = 1; i <= n; i++) {
        s[i] = s[i - 1] ^ a[i];
        insert(s[i]);
        // cout << s[i] << " ";
    }
    // cout << endl;
    ll ans = 0;
    priority_queue<Node> pq;
    for (int i = 0; i <= n; i++) {
        pq.push((Node){query(s[i], 1), 1, i});
    }
    k *= 2;
    while (k--) {
        auto temp = pq.top();
        pq.pop();
        ans += temp.val;
        pq.push((Node){query(s[temp.id], temp.t + 1), temp.t + 1, temp.id});
    }
    cout << ans / 2 << endl;
    return 0;
}

\(\color{#115}{NOI/NOI+/CTSC}\)

字符串

\(\color{#E91}{普及-}\)

\(\color{#FC1}{普及/提高-}\)

P1481 魔族密码

Trie，

题意

求输入 \(n\leq 2000\) 串中前串为后串前缀的最长串链长度。

思路

• 将所有串插入 Trie 末尾打标记，再查询每个串记录沿途经过的标记数，取最大值

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/
const int N = 2010;

int son[N][26], idx;        // idx存放节点编号， 0号节点既是根也是空节点
int cnt[N];         

void insert(const char str[]){    // 插入
    int p = 0, dep = 0;
    for(int i = 0; str[i]; i++){
        int u = str[i] - 'a';
        if(!son[p][u]) son[p][u] = ++ idx;      // 节点不存在则新建一个
        p = son[p][u];
    }
    cnt[p] ++;  // 对末尾节点做标记
}

int query(const char str[]){      // 查询
    int p = 0;
    ll res = 0;
    for(int i = 0; str[i]; i++){
        int u = str[i] - 'a';
        if(!son[p][u])  return 0;
        p = son[p][u];
        res += cnt[p];
    }
    return res;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n, ans = 0;
    cin >> n;
    vector<string> v(n);
    for (auto & s : v) {
        cin >> s;
        insert(s.c_str());
    }
    for (auto & s: v) {
        ans = max(ans, query(s.c_str()));
    }
    cout << ans << endl;
    return 0;
}

\(\color{#6B1}{普及+/提高}\)

\(\color{#48D}{提高+/省选-}\)

P1368 【模板】最小表示法

最小表示法，模板

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

int min_show(vector<int>& s, int len) {   // 下标从0开始
    int k = 0, i = 0, j = 1;
    while (k < len && i < len && j < len)
    {
        if (s[(i + k) % len] == s[(j + k) % len]) k++;
        else {
            s[(i + k) % len] > s[(j + k) % len] ? i = i + k + 1 : j = j + k + 1;
            if (i == j) i++;
            k = 0;
        }
    }
    return min(i, j);
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; i++)
        cin >> a[i];
    int ans = min_show(a, n);
    for (int i = 0; i < n; i++)
        cout << a[(i + ans) % n] << " ";
    
    return 0;
}

P1659 [国家集训队]拉拉队排练

题意

一个阳光明媚的早晨，雨荨带领拉拉队的队员们开始了排练。n个女生从左到右排成一行，每个人手中都举了一个写有26个小写字母中的某一个的牌子，在比赛的时候挥舞，为小伙子们呐喊、加油。

雨荨发现，如果连续的一段女生，有奇数个，并且他们手中的牌子所写的字母，从左到右和从右到左读起来一样，那么这一段女生就被称作和谐小群体。

现在雨荨想找出所有和谐小群体，并且按照女生的个数降序排序之后，前K个和谐小群体的女生个数的乘积是多少。由于答案可能很大，雨荨只要你告诉她，答案除以 \(19930726\) 的余数是多少就行了。

第一行为两个正整数 \(n\) 和 \(K\) ，代表的东西在题目描述中已经叙述。

接下来一行为 \(n\) 个字符，代表从左到右女生拿的牌子上写的字母。

输出一个整数，代表题目描述中所写的乘积除以19930726的余数，如果总的和谐小群体个数小于K，输出一个整数-1。

数据范围

测试点	n	K
1	10	10
2-3	100	100
4-7	1,000	1,000
8	100,000	= 1
9-11	100,000	100,000
12-14	100,000	1,000,000,000,000
15-17	500,000	1,000,000,000,000
18	1,000,000	= 1
19	1,000,000	1,000,000
20	1,000,000	1,000,000,000,000

思路

• 用 Manacher 找出奇数长度的回文串的回文半径，记录出现次数映射到值域数组上
• 从大到小遍历值域数组，并用快速幂优化速度即可

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

const int N = 1e6 + 100, mod = 19930726;
char s[N];
int cnt[N];
struct Manacher
{
    vector<int> lc;
    vector<char> ch;
    int len, n;
    Manacher(char *s, int _n): lc(2 * _n + 5), ch(2 * _n + 5), n(_n)  { init(s); manacher(); }
    /* s 1 bas , Manacher manacher(s), original_length = lc[i] - 1*/
    void init(char *s) {
        ch[n * 2 + 1] = '#';
        ch[0] = '@';
        ch[n * 2 + 2] = '\0';
        for (int i = n; i >= 1; i--) {
            ch[i * 2] = s[i], ch[i * 2 - 1] = '#';
        }
        len = 2 * n + 1;
    }
    void manacher() {
        lc[1] = 1;
        int k = 1;      // k 是 最右子串 回文中心
        for (int i = 2; i <= len; i++) {
            int p = k + lc[k] - 1;  // 最右子串 R
            if (i <= p) {   // 在最右子串内, 继承对称点的回文半径
                lc[i] = min(lc[2 * k - i], p - i + 1);
            }
            else {
                lc[i] = 1;
            }
            while (ch[i + lc[i]] == ch[i - lc[i]])      // 暴力拓展
                lc[i]++;
            if (i + lc[i] > k + lc[k])  
                k = i;
        }
    }
    void debug() {
        for (int i = 1; i <= len; i++) 
            i == len ? cout << ch[i] << "\n" : cout << ch[i];
        for (int i = 1; i <= len; i++) {
            cout << "lc[" << i << "]" << "=" << lc[i] << "\n";
        }
    }
};

ll qmi(ll a, ll k, int mod) {
    ll res = 1;
    while (k) {
            if (k & 1)
                    res = res * a % mod;
            a = a * a % mod;
            k >>= 1;
    }
    return res;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    ll n, k;
    cin >> n >> k;
    cin >> (s + 1);
    Manacher ches(s, n);
    ll tot = 0;
    int mx = 0;
    for (int i = 1; i <= n; i++) {
        int x = ches.lc[i * 2];
        tot += x / 2;
        cnt[ches.lc[i * 2]] ++;
        mx = max(mx, ches.lc[i * 2]);
    }
    if (k > tot) {
        cout << -1 << endl;
        return 0;
    }
    ll ans = 1;
    for (int i = mx; i && k; i--) {
        if (k >= cnt[i]) {
            ans = ans * qmi(i - 1, cnt[i], mod) % mod;
            k -= cnt[i];
            if (i >= 2)
                cnt[i - 2] += cnt[i];
        }
        else {
            ans = ans * qmi(i - 1, k, mod) % mod;
            k = 0;
        }
    }
    cout << ans << endl;
    return 0;
}

P2870 [USACO007DEC]Best Cow Line G

后缀数组、从字符串首尾取字符最小化字典序

题意

Farmer John 打算带领 \(N\)（\(1 \leq N \leq 5 \times 10^5\)）头奶牛参加一年一度的”全美农场主大奖赛“。在这场比赛中，每个参赛者必须让他的奶牛排成一列，然后带领这些奶牛从裁判面前依此走过。

今年，竞赛委员会在接受报名时，采用了一种新的登记规则：取每头奶牛名字的首字母，按照它们在队伍中的次序排成一列。将所有队伍的名字按字典序升序排序，从而得到出场顺序。

FJ 由于事务繁忙，他希望能够尽早出场。因此他决定重排队列。

他的调整方式是这样的：每次，他从原队列的首端或尾端牵出一头奶牛，将她安排到新队列尾部。重复这一操作直到所有奶牛都插入新队列为止。

现在请你帮 FJ 算出按照上面这种方法能排出的字典序最小的队列。

第一行一个整数 \(N\)。
接下来 \(N\) 行每行一个大写字母，表示初始队列。

输出一个长度为 \(N\) 的字符串，表示可能的最小字典序队列。
每输出 \(80\) 个字母需要一个换行。

数据范围
\(1\leq N \leq 5 * 10^5\)

思路

• 优化暴力，每次从正尾取是看正串和反串谁小，那么我们就把字符串拼成正串+反串，跑一次 SA。
• 记录首尾位置，比较对应的“后缀”字典序即可！
• 复杂度 \(O(nlogn)\)

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

#define RMQ
const int maxn = 1e6 + 10;
struct SA {
    #ifndef RMQ
    struct Segment_Tree {
        #define ls u << 1
        #define rs u << 1 | 1
        int min_val[maxn << 2];
        void pushup(int u) {
            min_val[u] = min(min_val[ls], min_val[rs]);
        }
        void build(int u, int l, int r, int* h) {
            if (l == r) {
                min_val[u] = h[l];
                return ;
            }
            int mid = (l + r) >> 1;
            build(ls, l, mid, h), build(rs, mid + 1, r, h);
            pushup(u);
        }
        int query(int u, int l, int r, int ql, int qr) {
            if (l > qr || ql > r) return 0x3f3f3f3f;
            if (ql <= l && r <= qr) return min_val[u];
            int mid = (l + r) >> 1;
            return min(query(ls, l, mid, ql, qr), query(rs, mid + 1, r, ql, qr));
        }
    }segtree;
    #else
    int st[maxn][20], lg[maxn];
    void init_st() {
        for (int i = 2; i < maxn; i++) lg[i] = lg[i / 2] + 1;
        for (int i = 1; i <= n; ++i) st[i][0] = height[i];
        for (int j = 1; (1 << j) <= n; ++j) {
            for (int i = 1; i <= (n - (1 << j) + 1); ++i) {
                st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
            }
        }
    }
    #endif
    /*height[i] = lcp(S[sa[i]],S[sa[i-1]]), h[i]=height[rk[i]], h[i]>=h[i-1]-1, lcp(s[i],s[j])=min(height[rk[i]+1],...,height[rk[j]])*/
    int n, sa[maxn], rk[maxn], id[maxn], cnt[maxn], height[maxn], px[maxn];   
    void get_sa(const char* s, int _n) {    // get sa and height
        n = _n;
        int m = 300, p = 0;      // m 是值域, 初始化为字符集大小
        for (int i = 0; i <= m; i++) cnt[i] = 0;
        for (int i = 1; i <= n; ++i) cnt[rk[i] = (int)s[i]] ++; // 先对1个字符大小的子串进行计数排序
        for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
        for (int i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
        for (int w = 1; w <= n; w <<= 1, m = p, p = 0) { // m=p 就是优化计数排序值域
            for (int i = n - w + 1; i <= n; ++i) // 第二关键字无穷小先放进去
                id[++p] = i;
            for (int i = 1; i <= n; ++i) 
                if (sa[i] > w) id[++p] = sa[i] - w; // 顺次放入 s[sa[i]-w] 的第二关键字排名
            for (int i = 0; i <= m; ++i) cnt[i] = 0;
            for (int i = 1; i <= n; ++i) ++cnt[rk[i]], px[i] = rk[id[i]];  
            for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
            for (int i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
            for (int i = 1; i <= n; ++i) swap(rk[i], id[i]);
            rk[sa[1]] = p = 1;
            for (int i = 2; i <= n; ++i) {
                rk[sa[i]] = (id[sa[i]] == id[sa[i - 1]] && id[sa[i] + w] == id[sa[i - 1] + w] ? p : ++p);
            }
            if (p >= n) {       // 排名已经更新出来了
                break;
            }
        }
    }
    void get_height(const char* s){
        for (int i = 1, k = 0; i <= n; ++i) {       // 获取 height数组
            if (k) --k;
            int j = sa[rk[i] - 1];
            while (s[i + k] == s[j + k]) ++k;
            height[rk[i]] = k;
        }
#ifdef _DEBUG
        for (int i = 1; i <= n; ++i) 
            cout<<"height["<<i<<"] = "<<height[i]<<endl;
#endif
    }

    void init() {
#ifndef RMQ
        segtree.build(1, 1, n, height);
#else
        init_st();
#endif
    }
    int get_lcp(int x, int y) {
        int rkx = rk[x], rky = rk[y];
        if (rkx > rky) swap(rkx, rky);
        rkx++;
#ifndef RMQ
        int lcp = segtree.query(1, 1, n, rkx, rky);
#else
        int k = lg[(rky - rkx + 1)];
        int lcp = min(st[rkx][k], st[rky - (1 << k) + 1][k]);
#endif

#ifdef _DEBUG
        cout<<"[getlcp] x="<<x<<" y="<<y<<" rkx="<<rkx<<" rky="<<rky<<" lcp="<<lcp<<endl;
#endif
        return lcp;
    }
}sa;

/*
ACDBCB
首尾一样，看下一个字符
ACDBCB
BCBDCA
CBDCA
$$BDCA
CDBCB
DBCB
*/

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    string s;
    for (int i = 0; i < n; i++) {
        char c;
        cin >> c;
        s += c;
    }
    auto t = s;
    reverse(arr(t));
    s = " " + s + t;
    sa.get_sa(s.c_str(), n * 2);
    int head = 1, tail = 1;
    int cnt = n;
    vector<char> ans;
    // cout << s << endl;
    while (cnt--) {
        if (sa.rk[head] < sa.rk[n + tail]) {
            ans.pb(s[head++]);
        }
        else {
            ans.pb(s[n + tail]);
            tail++;
        }
    }
    for (int i = 0; i < (int)ans.size(); i++) {
        if (i % 80 == 0 && i)
            cout << endl;
        cout << ans[i];
    }
    return 0;
}

P2922 [USACO08DEC]Secret Message G

Trie, 水题

题意

贝茜正在领导奶牛们逃跑．为了联络，奶牛们互相发送秘密信息．

信息是二进制的，共有 \(M\)（\(1 \le M \le 50000\)）条，反间谍能力很强的约翰已经部分拦截了这些信息，知道了第 \(i\) 条二进制信息的前 \(b_i\)（\(l \le b_i \le 10000\)）位，他同时知道，奶牛使用 \(N\)（\(1 \le N \le 50000\)）条暗号．但是，他仅仅知道第 \(j\) 条暗号的前 \(c_j\)（\(1 \le c_j \le 10000\)）位。

对于每条暗号 \(j\)，他想知道有多少截得的信息能够和它匹配。也就是说，有多少信息和这条暗号有着相同的前缀。当然，这个前缀长度必须等于暗号和那条信息长度的较小者。

在输入文件中，位的总数（即 \(\sum b_i + \sum c_i\)）不会超过 \(500000\)。

思路

• 建立 Trie 解决前缀问题是显然的，通过所有信息建 Trie
• 将每个暗号放到 Trie 上跑，对应答案为 途径路径的结尾数 + 暗号结尾的子树中标记个数。

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define fi first
#define se second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

const int N = 10010, M = 500010;
int son[M][2], idx, m, n;        // idx存放节点编号， 0号节点既是根也是空节点
int cnt[M * 2], sz[M * 2];

void insert(vector<int> str){    // 插入
    int p = 0;
    for (auto u: str) {
        if(!son[p][u]) son[p][u] = ++ idx;      // 节点不存在则新建一个
        p = son[p][u];
        sz[p]++;
    }
    cnt[p] ++;  // 对末尾节点做标记
}

ll query(vector<int> str){      // 查询
    int p = 0;
    ll res = 0;
    for (auto u: str) {
        if(!son[p][u])  return res;
        p = son[p][u];
        res += cnt[p];
    }
    res += sz[p] - cnt[p];
    return res;
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> m >> n;
    for (int i = 1; i <= m; i++) {
        int k;
        cin >> k;
        vector<int> v(k);
        for (auto &t: v)
            cin >> t;
        insert(v);
    }
    for (int i = 1, k; i <= n; i++) {
        cin >> k;
        vector<int> v(k);
        for (auto &t: v)
            cin >> t;
        cout << query(v) << endl;
    }
    return 0;
}

P3501 [POI2010]ANT-Antisymmetry

Manacher 板子，思维

题意

对于一个 01 字符串，如果将这个字符串 0 和 1 取反后，再将整个串反过来和原串一样，就称作“反对称”字符串。比如00001111和010101就是反对称的，1001就不是。

现在给出一个长度为 \(N\) 的 01 字符串，求它有多少个子串是反对称的。

数据范围
\(n\leq 5 * 10^5\)

思路

• 反对称的实际含义，0 和 1 相对应，其实是替代了 Manacher 原来的相等定义。
• 根据题目性质，反对称不包含奇数长度的串，做 Manacher 只关心奇数长度的串的回文中心。
• 0 '=' 1, '#' = '#', 套上 Manacher 板子即可

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

const int N = 5e5 + 100;
char s[N];
ll ans;

struct Manacher
{
    int lc[2 * N];
    char ch[2 * N], mp[500];
    int len;
    Manacher(char *s) { init(s); manacher(); }
    /* s 1 bas , Manacher manacher(s)*/
    void init(char *s) {
        int n = strlen(s + 1);
        ch[n * 2 + 1] = '#';
        ch[0] = '@';
        ch[n * 2 + 2] = '\0';
        for (int i = n; i >= 1; i--) {
            ch[i * 2] = s[i], ch[i * 2 - 1] = '#';
        }
        len = 2 * n + 1;
        mp[int('#')] = '#', mp[int('@')] = '@', mp[int('1')] = '0', mp[int('0')] = '1';
    }

    void manacher() {
        lc[1] = 1;
        int k = 1;      // k 是 最右子串 回文中心
        for (int i = 1; i <= len; i += 2) {
            int p = k + lc[k] - 1;  // 最右子串 R
            if (i <= p) {   // 在最右子串内, 继承对称点的回文半径
                lc[i] = min(lc[2 * k - i], p - i + 1);
            }
            else {
                lc[i] = 1;
            }
            while (ch[i + lc[i]] == mp[int(ch[i - lc[i]])])      // 暴力拓展
                lc[i]++;
            if (i + lc[i] > k + lc[k])  
                k = i;
            ans += lc[i] / 2;
        }
    }
    void debug() {
        for (int i = 1; i <= len; i++) 
            i == len ? cout << ch[i] << "\n" : cout << ch[i];
        for (int i = 1; i <= len; i++) {
            cout << "lc[" << i << "]" << "=" << lc[i] << "\n";
        }
    }
};

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    cin >> (s + 1);
    Manacher ches(s);
    cout << ans << endl;
    return 0;
}

P4287 [SHOI2011]双倍回文

题意

记字符串 \(w\) 的倒置为 \(w^R\) 。例如 \((abcd)^R=dcba\)， \((abba)^R=abba\)。

对字符串x，如果 \(x\) 满足 \(x^R=x\) ，则称之为回文；例如abba是一个回文，而abed不是。

如果x能够写成的 \(ww^Rww^R\) 形式，则称它是一个“双倍回文”。换句话说，若要 \(x\) 是双倍回文，它的长度必须是 \(4\) 的倍数，而且 \(x\) ， \(x\) 的前半部分，\(x\) 的后半部分都要是回文。例如\(abbaabba\)是一个双倍回文，而 \(abaaba\) 不是，因为它的长度不是 \(4\) 的倍数。

\(x\) 的子串是指在\(x\)中连续的一段字符所组成的字符串。例如 \(be\) 是 \(abed\) 的子串，而 \(ac\) 不是。

\(x\) 的回文子串，就是指满足回文性质的 \(x\) 的子串。

\(x\) 的双倍回文子串，就是指满足双倍回文性质的 \(x\) 的子串。

你的任务是，对于给定的字符串，计算它的最长双倍回文子串的长度。

输入分为两行。

第一行为一个整数，表示字符串的长度。
第二行有个连续的小写的英文字符，表示字符串的内容。

输出文件只有一行，即：输入数据中字符串的最长双倍回文子串的长度，如果双倍回文子串不存在，则输出\(0\)。

数据范围
\(N \le 500000\)

思路

• 如果一个回文串是双回文串，对于右边的回文串的中心 \(i\) 被 Manacher 遍历 到时，最右回文串半径 \(r >i\)。
• 判断中心 \(i\) 的回文半径是否与最右回文串中心 \(k\) 相交集即可更新双回文串长度。
• 双回文串中心一定是 # ，因为长度为偶数, 因此只处理偶数长度位置

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

const int N = 5e5 + 100;
char s[N];
int ans;

struct Manacher
{
    vector<int> lc;
    vector<char> ch;
    int len, n;
    Manacher(char *s, int _n): lc(2 * _n + 5), ch(2 * _n + 5), n(_n) { init(s); manacher(); }
    /* s 1 bas , Manacher manacher(s), original_length = lc[i] - 1*/
    void init(char *s) {
        ch[n * 2 + 1] = '#';
        ch[0] = '@';
        ch[n * 2 + 2] = '\0';
        for (int i = n; i >= 1; i--) {
            ch[i * 2] = s[i], ch[i * 2 - 1] = '#';
        }
        len = 2 * n + 1;
    }
    void manacher() {
        lc[1] = 1;
        int k = 1;      // k 是 最右子串 回文中心
        for (int i = 1; i <= len; i += 2) {
            int p = k + lc[k] - 1;  // 最右子串 R
            if (i <= p) {   // 在最右子串内, 继承对称点的回文半径
                lc[i] = min(lc[2 * k - i], p - i + 1);
            }
            else {
                lc[i] = 1;
            }
            if (i < p && i - lc[i] < k)
                ans = max(ans, 2 * (i - k));
            while (ch[i + lc[i]] == ch[i - lc[i]])      // 暴力拓展
                lc[i]++;
            if (i + lc[i] > k + lc[k])  {
                k = i;
            }
        }
    }
    void debug() {
        for (int i = 1; i <= len; i++) 
            i == len ? cout << ch[i] << "\n" : cout << ch[i];
        for (int i = 1; i <= len; i++) {
            cout << "lc[" << i << "]" << "=" << lc[i] << "\n";
        }
    }
};

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    cin >> n;
    cin >> (s + 1);
    Manacher ches(s, n);
    // ches.debug();
    cout << ans << endl;
    return 0;
}

P4555 [国家集训队]最长双回文串

单调队列（线段树）实现区间 min 操作，Manacher

题意

顺序和逆序读起来完全一样的串叫做回文串。比如acbca是回文串，而abc不是（abc的顺序为abc，逆序为cba，不相同）。

输入长度为 \(n\) 的串 \(S\) ，求 \(S\) 的最长双回文子串 \(T\) ,即可将 \(T\) 分为两部分 \(X\)，\(Y\)，（\(|X|,|Y|≥1\)）且 \(X\) 和 \(Y\) 都是回文串。

数据范围
\(2\leq |S| \leq 10^5\)

思路

• 对于每个双回文串，左右两个子串都是回文串。整个串最长，等价于左右两个子串最长
• 可以枚举每个拼接点（两字母之间的位置，马拉车后的 # 位置），记录能覆盖每个点的最左回文中心和最右回文中心，两回文中心距离就是双回文串的长度
• 先做一次 Manacher，用类似单调队列的思想，对每个点的最左最右回文中心进行更新
• 注意最左边和最右边的 # 都是不合法的。

Soultion

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

const int N = 2e5 + 100;
char s[N];
struct Manacher
{
    int lc[2 * N];
    char ch[2 * N];
    int len;
    Manacher(char *s) { init(s); manacher(); }
    /* s 1 bas , Manacher manacher(s), original_length = lc[i] - 1*/
    void init(char *s) {
        int n = strlen(s + 1);
        ch[n * 2 + 1] = '#';
        ch[0] = '@';
        ch[n * 2 + 2] = '\0';
        for (int i = n; i >= 1; i--) {
            ch[i * 2] = s[i], ch[i * 2 - 1] = '#';
        }
        len = 2 * n + 1;
    }
    void manacher() {
        lc[1] = 1;
        int k = 1;      // k 是 最右子串 回文中心
        for (int i = 2; i <= len; i++) {
            int p = k + lc[k] - 1;  // 最右子串 R
            if (i <= p) {   // 在最右子串内, 继承对称点的回文半径
                lc[i] = min(lc[2 * k - i], p - i + 1);
            }
            else {
                lc[i] = 1;
            }
            while (ch[i + lc[i]] == ch[i - lc[i]])      // 暴力拓展
                lc[i]++;
            if (i + lc[i] > k + lc[k])  
                k = i;
        }
    }
    void debug() {
        for (int i = 1; i <= len; i++) 
            i == len ? cout << ch[i] << "\n" : cout << ch[i];
        for (int i = 1; i <= len; i++) {
            cout << "lc[" << i << "]" << "=" << lc[i] << "\n";
        }
    }
};

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> (s + 1);
    Manacher ches(s);
    vector<int> fl(ches.len + 1, 0);
    vector<int> fr(ches.len + 1, 0);
    deque<PII> q;
    // ches.debug();
    for (int i = 1; i <= ches.len; i++) {
        while (!q.empty() && q.front().y < i - q.front().x + 1) q.pop_front();
        q.push_back({i, ches.lc[i]});
        fl[i] = q.front().x;
    }
    q.clear();
    for (int i = ches.len; i ; i--) {
        while (!q.empty() && q.front().y < q.front().x - i + 1) q.pop_front();
        q.push_back({i, ches.lc[i]});
        fr[i] = q.front().x;
    }
    int ans = 0;
    for (int i = 3; i < ches.len; i += 2){
        // cout << i << " " << fl[i] << " " << fr[i] << endl;
        ans = max(ans, fr[i] - fl[i]);
    }
    if (ans == 1) ans = 0;
    cout << ans << endl;
    return 0;
}

\(\color{#83C}{省选+/NOI-}\)

P2408 不同子串个数

后缀数组模板题，求本质不同子串的个数

题意

给你一个长为 \(n\) 的字符串，求不同的子串的个数。

我们定义两个子串不同，当且仅当有这两个子串长度不一样或者长度一样且有任意一位不一样。

子串的定义：原字符串中连续的一段字符组成的字符串。

第一行一个整数 \(n\)。
接下来一行 \(n\) 个字符表示给出的字符串。

一行一个整数，表示不一样的子串个数。

数据范围

• 对于 \(30\%\) 的数据，保证 \(n\le 1000\)。
• 对于 \(100\%\) 的数据，保证 \(1 \leq n \le 10^5\)，字符串中只有小写英文字母。

思路

• 按字典序从小到大枚举所有后缀，统计有多少个新出现的前缀即可。
• 对于排名第 i 的后缀 \(S[sa[i], n]\)，共有 \(n - sa[i] + 1\) 个前缀，其中有 \(Height[i]\)
  个前缀同时出现在前一个排名的后缀 \(S[sa[i-1], n]\) 中，因此减掉即可。
• 上述证明是不完整的，还需要证明所有在 S[sa[i], n] 中出现，但没有在
  \(S[sa[i-1], n]\) 中出现的前缀，他们在所有更小排名的后缀串也都没有出
  现。
• 证明就是，如果出现过会破坏我们求 \(lcp\) 时的性质。

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

#define RMQ
const int maxn = 1e6 + 10;
struct SA {
    #ifndef RMQ
    struct Segment_Tree {
        #define ls u << 1
        #define rs u << 1 | 1
        int min_val[maxn << 2];
        void pushup(int u) {
            min_val[u] = min(min_val[ls], min_val[rs]);
        }
        void build(int u, int l, int r, int* h) {
            if (l == r) {
                min_val[u] = h[l];
                return ;
            }
            int mid = (l + r) >> 1;
            build(ls, l, mid, h), build(rs, mid + 1, r, h);
            pushup(u);
        }
        int query(int u, int l, int r, int ql, int qr) {
            if (l > qr || ql > r) return 0x3f3f3f3f;
            if (ql <= l && r <= qr) return min_val[u];
            int mid = (l + r) >> 1;
            return min(query(ls, l, mid, ql, qr), query(rs, mid + 1, r, ql, qr));
        }
    }segtree;
    #else
    int st[maxn][20], lg[maxn];
    void init_st() {
        for (int i = 2; i < maxn; i++) lg[i] = lg[i / 2] + 1;
        for (int i = 1; i <= n; ++i) st[i][0] = height[i];
        for (int j = 1; (1 << j) <= n; ++j) {
            for (int i = 1; i <= (n - (1 << j) + 1); ++i) {
                st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
            }
        }
    }
    #endif
    /*height[i] = lcp(S[sa[i]],S[sa[i-1]]), h[i]=height[rk[i]], h[i]>=h[i-1]-1, lcp(s[i],s[j])=min(height[rk[i]+1],...,height[rk[j]])*/
    int n, sa[maxn], rk[maxn], id[maxn], cnt[maxn], height[maxn], px[maxn];   
    void get_sa(const char* s, int _n) {    // get sa and height
        n = _n;
        int m = 300, p = 0;      // m 是值域, 初始化为字符集大小
        for (int i = 0; i <= m; i++) cnt[i] = 0;
        for (int i = 1; i <= n; ++i) cnt[rk[i] = (int)s[i]] ++; // 先对1个字符大小的子串进行计数排序
        for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
        for (int i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
        for (int w = 1; w <= n; w <<= 1, m = p, p = 0) { // m=p 就是优化计数排序值域
            for (int i = n - w + 1; i <= n; ++i) // 第二关键字无穷小先放进去
                id[++p] = i;
            for (int i = 1; i <= n; ++i) 
                if (sa[i] > w) id[++p] = sa[i] - w; // 顺次放入 s[sa[i]-w] 的第二关键字排名
            for (int i = 0; i <= m; ++i) cnt[i] = 0;
            for (int i = 1; i <= n; ++i) ++cnt[rk[i]], px[i] = rk[id[i]];  
            for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
            for (int i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
            for (int i = 1; i <= n; ++i) swap(rk[i], id[i]);
            rk[sa[1]] = p = 1;
            for (int i = 2; i <= n; ++i) {
                rk[sa[i]] = (id[sa[i]] == id[sa[i - 1]] && id[sa[i] + w] == id[sa[i - 1] + w] ? p : ++p);
            }
            if (p >= n) {       // 排名已经更新出来了
                break;
            }
        }
    }
    void get_height(const char * s){
        for (int i = 1, k = 0; i <= n; ++i) {       // 获取 height数组
            if (k) --k;
            int j = sa[rk[i] - 1];
            while (s[i + k] == s[j + k]) ++k;
            height[rk[i]] = k;
        }
#ifdef _DEBUG
        for (int i = 1; i <= n; ++i) 
            cout<<"height["<<i<<"] = "<<height[i]<<endl;
#endif
    }

    void init() {
#ifndef RMQ
        segtree.build(1, 1, n, height);
#else
        init_st();
#endif
    }
    int get_lcp(int x, int y) {
        int rkx = rk[x], rky = rk[y];
        if (rkx > rky) swap(rkx, rky);
        rkx++;
#ifndef RMQ
        int lcp = segtree.query(1, 1, n, rkx, rky);
#else
        int k = lg[(rky - rkx + 1)];
        int lcp = min(st[rkx][k], st[rky - (1 << k) + 1][k]);
#endif

#ifdef _DEBUG
        cout<<"[getlcp] x="<<x<<" y="<<y<<" rkx="<<rkx<<" rky="<<rky<<" lcp="<<lcp<<endl;
#endif
        return lcp;
    }
}sa;

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n;
    string s;
    cin >> n;
    cin >> s;
    s = " " + s;
    sa.get_sa(s.c_str(), n);
    sa.get_height(s.c_str());
    ll ans = 0;
    for (int i = 1; i <= n; i++) {
        ans += n - sa.sa[i] + 1 - sa.height[i];
    }
    cout << ans << endl;
    return 0;
}

P2852 [USACO06DEC]Milk Patterns G

后缀数组, heigt数组应用，查询出现 \(k\) 次子串的最大长度

题意
农夫John发现他的奶牛产奶的质量一直在变动。经过细致的调查，他发现：虽然他不能预见明天产奶的质量，但连续的若干天的质量有很多重叠。我们称之为一个“模式”。 John的牛奶按质量可以被赋予一个0到1000000之间的数。并且John记录了N(1<=N<=20000)天的牛奶质量值。他想知道最长的出现了至少K(2<=K<=N)次的模式的长度。比如1 2 3 2 3 2 3 1 中 2 3 2 3出现了两次。当K=2时，这个长度为4。

思路

• 一个字符串出现 \(K\) 次表明在相邻的 \(k-1\) 个 height 数组中均出现。
• 那么只需要查找相邻 \(k-1\) 个 height 数组的最小值的最大值即可，单调队列能 \(O(n)\), 也可以用区间最值查询。

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double jb;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

#define RMQ
// #define _DEBUG
const int maxn = 1e6 + 10;
struct SA {
#ifndef RMQ
    struct Segment_Tree {
        #define ls u << 1
        #define rs u << 1 | 1
        int min_val[maxn << 2];
        void pushup(int u) {
            min_val[u] = min(min_val[ls], min_val[rs]);
        }
        void build(int u, int l, int r, int* h) {
            if (l == r) {
                min_val[u] = h[l];
                return ;
            }
            int mid = (l + r) >> 1;
            build(ls, l, mid, h), build(rs, mid + 1, r, h);
            pushup(u);
        }
        int query(int u, int l, int r, int ql, int qr) {
            if (l > qr || ql > r) return 0x3f3f3f3f;
            if (ql <= l && r <= qr) return min_val[u];
            int mid = (l + r) >> 1;
            return min(query(ls, l, mid, ql, qr), query(rs, mid + 1, r, ql, qr));
        }
    }segtree;
#else
    int st[maxn][20], lg[maxn];
    void init_st() {
        for (int i = 2; i < maxn; i++) lg[i] = lg[i / 2] + 1;
        for (int i = 1; i <= n; ++i) st[i][0] = height[i];
        for (int j = 1; (1 << j) <= n; ++j) {
            for (int i = 1; i <= (n - (1 << j) + 1); ++i) {
                st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
            }
        }
    }
#endif
    /*height[i] = lcp(S[sa[i]],S[sa[i-1]]), h[i]=height[rk[i]], h[i]>=h[i-1]-1, lcp(s[i],s[j])=min(height[rk[i]+1],...,height[rk[j]])*/
    int n, sa[maxn], rk[maxn], id[maxn], cnt[maxn], height[maxn], px[maxn];   
    void get_sa(int * s, int _n) {    // get sa and height
        n = _n;
        int m = 300, p = 0;      // m 是值域, 初始化为字符集大小
        for (int i = 0; i <= m; i++) cnt[i] = 0;
        for (int i = 1; i <= n; ++i) cnt[rk[i] = (int)s[i]] ++; // 先对1个字符大小的子串进行计数排序
        for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
        for (int i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
        for (int w = 1; w <= n; w <<= 1, m = p, p = 0) { // m=p 就是优化计数排序值域
            for (int i = n - w + 1; i <= n; ++i) // 第二关键字无穷小先放进去
                id[++p] = i;
            for (int i = 1; i <= n; ++i) 
                if (sa[i] > w) id[++p] = sa[i] - w; // 顺次放入 s[sa[i]-w] 的第二关键字排名
            for (int i = 0; i <= m; ++i) cnt[i] = 0;
            for (int i = 1; i <= n; ++i) ++cnt[rk[i]], px[i] = rk[id[i]];  
            for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
            for (int i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
            for (int i = 1; i <= n; ++i) swap(rk[i], id[i]);
            rk[sa[1]] = p = 1;
            for (int i = 2; i <= n; ++i) {
                rk[sa[i]] = (id[sa[i]] == id[sa[i - 1]] && id[sa[i] + w] == id[sa[i - 1] + w] ? p : ++p);
            }
            if (p >= n) {       // 排名已经更新出来了
                break;
            }
        }
    }
    void get_height(int * s){
        for (int i = 1, k = 0; i <= n; ++i) {       // 获取 height数组
            if (k) --k;
            int j = sa[rk[i] - 1];
            while (s[i + k] == s[j + k]) ++k;
            height[rk[i]] = k;
        }
#ifdef _DEBUG
        for (int i = 1; i <= n; ++i) 
            cout<<"height["<<i<<"] = "<<height[i]<<endl;
#endif
    }

    void init() {
#ifndef RMQ
        segtree.build(1, 1, n, height);
#else
        init_st();
#endif
    }
    int query(int x, int y) {
        int rkx = x, rky = y;
        // rkx++;
#ifndef RMQ
        int lcp = segtree.query(1, 1, n, rkx, rky);
#else
        int k = lg[(rky - rkx + 1)];
        int lcp = min(st[rkx][k], st[rky - (1 << k) + 1][k]);
#endif

#ifdef _DEBUG
        cout<<"[getlcp] x="<<x<<" y="<<y<<" rkx="<<rkx<<" rky="<<rky<<" lcp="<<lcp<<endl;
#endif
        return lcp;
    }
}sa;

int s[maxn];

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    int n, k;
    cin >> n >> k;
    for (int i = 1; i <= n; ++i) {
        cin >> s[i];
    }
    sa.get_sa(s, n);
    sa.get_height(s);
    sa.init();
    k --;
    int ans = 0;
    for (int i = 1; i + k - 1 <= n; i++) {
        ans = max(ans, sa.query(i, i + k - 1));
    }
    cout << ans << endl;
    return 0;
}

P4051 加密字符

题意

喜欢钻研问题的JS 同学，最近又迷上了对加密方法的思考。一天，他突然想出了一种他认为是终极的加密办法：把需要加密的信息排成一圈，显然，它们有很多种不同的读法。

例如‘JSOI07’，可以读作： JSOI07 SOI07J OI07JS I07JSO 07JSOI 7JSOI0 把它们按照字符串的大小排序： 07JSOI 7JSOI0 I07JSO JSOI07 OI07JS SOI07J 读出最后一列字符：I0O7SJ，就是加密后的字符串（其实这个加密手段实在很容易破解，鉴于这是突然想出来的，那就^^）。 但是，如果想加密的字符串实在太长，你能写一个程序完成这个任务吗？

输入文件包含一行，欲加密的字符串。注意字符串的内容不一定是字母、数字，也可以是符号等。

输出一行，为加密后的字符串。

数据范围
对于40%的数据字符串的长度不超过10000。
对于100%的数据字符串的长度不超过100000。

思路

• 想象一下经典的破坏成链的思路，用到字符串上，将 \(S=S+S\)
• 跑一下 SA，然后找长度大于 \(n\) 的后缀，字典序从小到大取第 \(n\) 个字符便是答案了。

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

/* 
07JSOI07
7JSOI07
I07JSOI07
JSOI07
OI07JSOI07
SOI07JSOI07
*/
#define RMQ
const int maxn = 2e5 + 10;
string s;
struct SA {
    #ifndef RMQ
    struct Segment_Tree {
        #define ls u << 1
        #define rs u << 1 | 1
        int min_val[maxn << 2];
        void pushup(int u) {
            min_val[u] = min(min_val[ls], min_val[rs]);
        }
        void build(int u, int l, int r, int* h) {
            if (l == r) {
                min_val[u] = h[l];
                return ;
            }
            int mid = (l + r) >> 1;
            build(ls, l, mid, h), build(rs, mid + 1, r, h);
            pushup(u);
        }
        int query(int u, int l, int r, int ql, int qr) {
            if (l > qr || ql > r) return 0x3f3f3f3f;
            if (ql <= l && r <= qr) return min_val[u];
            int mid = (l + r) >> 1;
            return min(query(ls, l, mid, ql, qr), query(rs, mid + 1, r, ql, qr));
        }
    }segtree;
    #else
    int st[maxn][20], lg[maxn];
    void init_st() {
        for (int i = 2; i < maxn; i++) lg[i] = lg[i / 2] + 1;
        for (int i = 1; i <= n; ++i) st[i][0] = height[i];
        for (int j = 1; (1 << j) <= n; ++j) {
            for (int i = 1; i <= (n - (1 << j) + 1); ++i) {
                st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
            }
        }
    }
    #endif
    /*height[i] = lcp(S[sa[i]],S[sa[i-1]]), h[i]=height[rk[i]], h[i]>=h[i-1]-1, lcp(s[i],s[j])=min(height[rk[i]+1],...,height[rk[j]])*/
    int n, sa[maxn], rk[maxn], id[maxn], cnt[maxn], height[maxn], px[maxn];   
    void get_sa(const char* s, int _n) {    // get sa and height
        n = _n;
        int m = 300, p = 0;      // m 是值域, 初始化为字符集大小
        for (int i = 0; i <= m; i++) cnt[i] = 0;
        for (int i = 1; i <= n; ++i) cnt[rk[i] = (int)s[i]] ++; // 先对1个字符大小的子串进行计数排序
        for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
        for (int i = n; i >= 1; --i) sa[cnt[rk[i]]--] = i;
        for (int w = 1; w <= n; w <<= 1, m = p, p = 0) { // m=p 就是优化计数排序值域
            for (int i = n - w + 1; i <= n; ++i) // 第二关键字无穷小先放进去
                id[++p] = i;
            for (int i = 1; i <= n; ++i) 
                if (sa[i] > w) id[++p] = sa[i] - w; // 顺次放入 s[sa[i]-w] 的第二关键字排名
            for (int i = 0; i <= m; ++i) cnt[i] = 0;
            for (int i = 1; i <= n; ++i) ++cnt[rk[i]], px[i] = rk[id[i]];  
            for (int i = 1; i <= m; ++i) cnt[i] += cnt[i - 1];
            for (int i = n; i >= 1; --i) sa[cnt[px[i]]--] = id[i];
            for (int i = 1; i <= n; ++i) swap(rk[i], id[i]);
            rk[sa[1]] = p = 1;
            for (int i = 2; i <= n; ++i) {
                rk[sa[i]] = (id[sa[i]] == id[sa[i - 1]] && id[sa[i] + w] == id[sa[i - 1] + w] ? p : ++p);
            }
            if (p >= n) {       // 排名已经更新出来了
                break;
            }
        }
    }
    void get_height(){
        for (int i = 1, k = 0; i <= n; ++i) {       // 获取 height数组
            if (k) --k;
            int j = sa[rk[i] - 1];
            while (s[i + k] == s[j + k]) ++k;
            height[rk[i]] = k;
        }
#ifdef _DEBUG
        for (int i = 1; i <= n; ++i) 
            cout<<"height["<<i<<"] = "<<height[i]<<endl;
        }
#endif
    }

    void init() {
#ifndef RMQ
        segtree.build(1, 1, n, height);
#else
        init_st();
#endif
    }
    int get_lcp(int x, int y) {
        int rkx = rk[x], rky = rk[y];
        if (rkx > rky) swap(rkx, rky);
        rkx++;
#ifndef RMQ
        int lcp = segtree.query(1, 1, n, rkx, rky);
#else
        int k = lg[(rky - rkx + 1)];
        int lcp = min(st[rkx][k], st[rky - (1 << k) + 1][k]);
#endif

#ifdef _DEBUG
        cout<<"[getlcp] x="<<x<<" y="<<y<<" rkx="<<rkx<<" rky="<<rky<<" lcp="<<lcp<<endl;
#endif
        return lcp;
    }
}sa;

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    cin >> s;
    int n = s.size();
    s = " " + s + s;
    sa.get_sa(s.c_str(), 2 * n);
    vector<char> ans;
    for (int i = 1; i <= 2 * n; i++) {
        if (sa.sa[i] <= n) {
            ans.pb(s[sa.sa[i] + n - 1]);
        }
    }
    for (auto c: ans)
        cout << c;
    return 0;
}

P5410 【模板】扩展 KMP（Z 函数）

Z algorithm 模板

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define endl "\n"
using namespace std;
/*----------------------------------------------------------------------------------------------------*/

const int N = 2e7 + 10;
// z[i]数组表示以i开始的后缀和前缀的最大匹配, 匹配时p#s跑一次

int z[2 * N];
void getz(const char *s, int len) {
    for (int i = 1; i <= len; i++) z[i] = 0;
    z[1] = len;
    for (int i = 2, l = 0, r = 0; i <= len; i++) {
        if (i <= r) z[i] = min(z[i - l + 1], r - i + 1);
        while (i + z[i] <= len && s[i + z[i]] == s[z[i] + 1]) ++ z[i];
        if (i + z[i] - 1 > r) l = i, r = i + z[i] - 1;
    }
}

int main() {
    ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
    string a, b;
    cin >> a >> b;
    int n = a.size(), m = b.size();
    b = " " + b;
    getz(b.c_str(), m);
    ll ans = 0;
    for (int i = 1; i <= m; i++) 
        ans ^= 1ll * i * (z[i] + 1);
    cout << ans << endl;
    string s = b + '#' + a;
    getz(s.c_str(), s.size() - 1);
    ans = 0;
    for (int i = m + 2; i <= n + m + 1; i++) 
        ans ^= 1ll * (i - (m + 1)) * (z[i] + 1);
    cout << ans << endl;
    return 0;
}

\(\color{#115}{NOI/NOI+/CTSC}\)

图论, 搜索

\(\color{#E91}{普及-}\)

\(\color{#FC1}{普及/提高-}\)

\(\color{#6B1}{普及+/提高}\)

CF796D Police Stations

多源 BFS 构造

题意

给定一棵 \(n\) 节点树，树上有 \(k\) 个点是警察局，要求所有点到最近的警察局的距离不大于d，求最多能删几条边

数据范围
保证所有点距离最近的警察局不超过 \(d\)
\(1\leq n,k \leq 3 * 10^5\)
\(0\leq d \leq n - 1\)

思路

• 首先所有点距离最近的警察局距离不超过 \(d\), 我们需要删除多余的边
• 可以尝试多源 BFS, 将所有警察局点放入队列中, 然后开搜, 如果遇到一个点已经被访问过, 根据bfs的性质, 我们现在处于的边就是可以删掉的边.
• 注意对遍历过的边的反向边特判, 具体见代码

Solution

#include<bits/stdc++.h>
typedef long long ll;
typedef unsigned long long ull;
typedef std::pair<int, int> PII;
typedef std::pair<ll, ll> PLL;
typedef double db;
#define arr(x) (x).begin(),(x).end()
#define x first
#define y second
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
const int N = 3e5 + 10;
bool st[N << 1];
int dist[N];
int n, k, d;
vector<PII> edge[N];

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	cin >> n >> k >> d;
	memset(dist, 0x3f, sizeof dist);
	queue<int> q;
	for(int i = 0; i < k; i++){
		int x;
		cin >> x;
		dist[x] = 0;
		q.push(x);
	}
	int cnt = 2;
	for(int i = 1; i < n; i++){
		int a, b;
		cin >> a >> b;
		edge[a].pb({b, cnt++});
		edge[b].pb({a, cnt++});
	}
	vector<int> res;
    while(q.size()){
		auto u = q.front();
		q.pop();
		for(auto v: edge[u]){
			if(st[v.y]) continue;
			if(dist[v.x] != 0x3f3f3f3f){
				res.pb(v.y / 2);
				st[v.y] = st[v.y ^ 1] = true;
				continue;
			}
			st[v.y] = st[v.y ^ 1] = true;
			dist[v.x] = dist[u] + 1;
			q.push(v.x);
		}
	}
	cout << res.size() << endl;
	for(auto t: res)
		cout << t << " ";
    return 0;
}	

\(\color{#48D}{提高+/省选-}\)

\(\color{#83C}{省选+/NOI-}\)

\(\color{#115}{NOI/NOI+/CTSC}\)

数学

\(\color{#E91}{普及-}\)

\(\color{#FC1}{普及/提高-}\)

\(\color{#6B1}{普及+/提高}\)

P5104 红包发红包

连续型数学期望

题意

这个抢红包系统是这样的：假如现在有w元，那么你抢红包能抢到的钱就是 \([0,w]\) 等概率均匀随机出的一个实数x。

现在红包发了一个 \(w\) 元的红包，有 \(n\) 个人来抢。那么请问第 \(k\) 个人期望抢到多少钱？

输出 \(mod(10^9 +7)\)。

思路

• 设第一次抢到红包数量为 \(x\), 对 \(x\) 做期望的积分, 第一次抢到 \(\frac{w}{2}\), 剩余 \(\frac{w}{2}\)
• 推一下发现每次抢到 \(\frac{w}{2^k}\)

#include<bits/stdc++.h>
typedef long long ll;
#define pb push_back
#define mkp make_pair
#define endl "\n"
using namespace std;
const int mod = 1e9 + 7;

ll qmi(ll a, ll k, int mod){
	ll res = 1;
	while(k){
		if(k & 1)
			res = res * a % mod;
		a = a * a % mod;
		k >>= 1;
	}
	return res;
}

int main(){
	ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
	ll w, n, k;
	cin >> w >> n >> k;
	// w / 2^k
	cout << w * qmi(qmi(2, k, mod), mod - 2, mod) % mod << endl;
    return 0;
}

\(\color{#48D}{提高+/省选-}\)

\(\color{#83C}{省选+/NOI-}\)

\(\color{#115}{NOI/NOI+/CTSC}\)

奇怪的题目

\(\color{#E91}{普及-}\)

\(\color{#FC1}{普及/提高-}\)

\(\color{#6B1}{普及+/提高}\)

\(\color{#48D}{提高+/省选-}\)

\(\color{#83C}{省选+/NOI-}\)

\(\color{#115}{NOI/NOI+/CTSC}\)