利用深度学习(Keras)进行癫痫分类-Python案例
本分享为脑机学习者Rose整理发表于公众号:脑机接口社区(微信号:Brain_Computer).QQ交流群:903290195

癫痫介绍
癫痫,即俗称“羊癫风”,是由多种病因引起的慢性脑功能障碍综合症,是仅次于脑血管病的第二大脑部疾病。癫痫发作的直接原因是脑部神经元反复地突发性过度放电所导致的间歇性中枢神经系统功能失调。临床上常表现为突然意识丧失、全身抽搐以及精神异常等。癫痫给患者带来巨大的痛苦和身心伤害,严重时甚至危及生命,儿童患者会影响到身体发育和智力发育。
脑电图是研究癫痫发作特征的重要工具,它是一种无创性的生物物理检查方法,所反映的信息是其他生理学方法所不能提供的。脑电图的分析主要是进行大脑异常放电活动的检测,包括棘波、尖波、棘.慢复合波等。目前,医疗工作者根据经验对患者的脑电图进行视觉检测,这项工作不仅非常耗时,而且由于人为分析具有主观性,不同专家对于同一记录的判断结果可能不同,从而导致误诊率上升。因此,利用自动检测、识别和预测技术对癫痫脑电进行及时、准确的诊断和预测,癫痫灶的定位和降低脑电数据的存储量是对癫痫脑电信号研究的重要内容[1]。
数据集
数据集: 癫痫发作识别数据集
下载地址:
https://archive.ics.uci.edu/ml/datasets/Epileptic+Seizure+Recognition
178个数据点的11,500个样本(178个数据点= 1秒的脑电图记录)11,500个具有5个类别的目标:1个代表癫痫发作波形,而2-5代表非癫痫发作波形.
Keras深度学习案例
代码参考整理于:
http://dy.163.com/v2/article/detail/EEC68EH5054281P3.html
#导入工具库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras import layers
from keras import regularizers
from sklearn.model_selection import train_test_split
from sklearn.metrics import roc_curve, auc
# 加载数据集
data = "data.csv"
df = pd.read_csv(data, header=0, index_col=0)
"""
查看数据集的head和信息
"""
print(df.head())
print(df.info())

"""
设置标签:
将目标变量转换为癫痫(y列编码为1)与非癫痫(2-5)
即将癫痫的目标变量设置为1,其他设置为标签0
"""
df["seizure"] = 0
for i in range(11500):
if df["y"][i] == 1:
df["seizure"][i] = 1
else:
df["seizure"][i] = 0
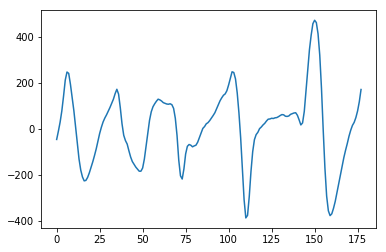
# 绘制并观察脑电波
plt.plot(range(178), df.iloc[11496,0:178])
plt.show()
"""
将把数据准备成神经网络可以接受的形式。
首先解析数据,
然后标准化值,
最后创建目标数组
"""
# 创建df1来保存波形数据点(waveform data points)
df1 = df.drop(["seizure", "y"], axis=1)
# 1. 构建11500 x 178的二维数组
wave = np.zeros((11500, 178))
z=0
for index, row in df1.iterrows():
wave[z,:] = row
z +=1
# 打印数组形状
print(wave.shape)
# 2. 标准化数据
"""
标准化数据,使其平均值为0,标准差为1
"""
mean = wave.mean(axis=0)
wave -= mean
std = wave.std(axis=0)
wave /= std
# 3. 创建目标数组
target = df["seizure"].values
(11500, 178)
"""
创建模型
"""
model = Sequential()
model.add(layers.Dense(64, activation="relu", kernel_regularizer=regularizers.l1(0.001), input_shape = (178,)))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(64, activation="relu", kernel_regularizer=regularizers.l1(0.001)))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation="sigmoid"))
model.summary()
"""
利用sklearn的train_test_split函数将所有的数据的20%作为测试集,其他的作为训练集
"""
x_train, x_test, y_train, y_test = train_test_split(wave, target, test_size=0.2, random_state=42)
#编译机器学习模型
model.compile(optimizer="rmsprop", loss="binary_crossentropy", metrics=["acc"])
"""
训练模型
epoch为100,
batch_size为128,
设置20%的数据集作为验证集
"""
history = model.fit(x_train, y_train, epochs=100, batch_size=128, validation_split=0.2, verbose=2)
# 测试数据(预测数据)
y_pred = model.predict(x_test).ravel()
# 计算ROC
fpr_keras, tpr_keras, thresholds_keras = roc_curve(y_test, y_pred)
# 计算 AUC
AUC = auc(fpr_keras, tpr_keras)
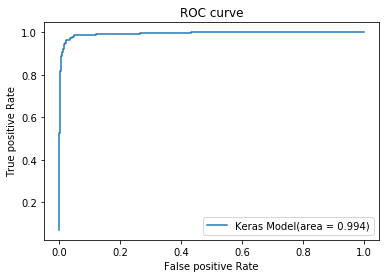
# 绘制 ROC曲线
plt.plot(fpr_keras, tpr_keras, label='Keras Model(area = {:.3f})'.format(AUC))
plt.xlabel('False positive Rate')
plt.ylabel('True positive Rate')
plt.title('ROC curve')
plt.legend(loc='best')
plt.show()
Model: "sequential_1"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense_1 (Dense) (None, 64) 11456
_________________________________________________________________
dropout_1 (Dropout) (None, 64) 0
_________________________________________________________________
dense_2 (Dense) (None, 64) 4160
_________________________________________________________________
dropout_2 (Dropout) (None, 64) 0
_________________________________________________________________
dense_3 (Dense) (None, 1) 65
=================================================================
Total params: 15,681
Trainable params: 15,681
Non-trainable params: 0
_________________________________________________________________
Train on 7360 samples, validate on 1840 samples
Epoch 1/100
- 0s - loss: 1.9573 - acc: 0.7432 - val_loss: 1.6758 - val_acc: 0.9098
Epoch 2/100
- 0s - loss: 1.5837 - acc: 0.8760 - val_loss: 1.3641 - val_acc: 0.9332
Epoch 3/100
- 0s - loss: 1.2899 - acc: 0.9201 - val_loss: 1.1060 - val_acc: 0.9424
Epoch 4/100
- 0s - loss: 1.0525 - acc: 0.9404 - val_loss: 0.9179 - val_acc: 0.9446
Epoch 5/100
- 0s - loss: 0.8831 - acc: 0.9466 - val_loss: 0.7754 - val_acc: 0.9484
Epoch 6/100
- 0s - loss: 0.7291 - acc: 0.9552 - val_loss: 0.6513 - val_acc: 0.9538
Epoch 7/100
- 0s - loss: 0.6149 - acc: 0.9572 - val_loss: 0.5541 - val_acc: 0.9495
Epoch 8/100
- 0s - loss: 0.5232 - acc: 0.9558 - val_loss: 0.4717 - val_acc: 0.9484
Epoch 9/100
- 0s - loss: 0.4443 - acc: 0.9595 - val_loss: 0.4118 - val_acc: 0.9489
Epoch 10/100
- 0s - loss: 0.3921 - acc: 0.9590 - val_loss: 0.3667 - val_acc: 0.9554
Epoch 11/100
- 0s - loss: 0.3579 - acc: 0.9553 - val_loss: 0.3348 - val_acc: 0.9565
Epoch 12/100
- 0s - loss: 0.3302 - acc: 0.9572 - val_loss: 0.3209 - val_acc: 0.9473
Epoch 13/100
- 0s - loss: 0.3154 - acc: 0.9546 - val_loss: 0.2988 - val_acc: 0.9560
Epoch 14/100
- 0s - loss: 0.2956 - acc: 0.9596 - val_loss: 0.2899 - val_acc: 0.9500
Epoch 15/100
- 0s - loss: 0.2907 - acc: 0.9565 - val_loss: 0.2786 - val_acc: 0.9500
Epoch 16/100
- 0s - loss: 0.2794 - acc: 0.9607 - val_loss: 0.2665 - val_acc: 0.9560
Epoch 17/100
- 0s - loss: 0.2712 - acc: 0.9588 - val_loss: 0.2636 - val_acc: 0.9598
Epoch 18/100
- 0s - loss: 0.2665 - acc: 0.9603 - val_loss: 0.2532 - val_acc: 0.9533
Epoch 19/100
- 0s - loss: 0.2659 - acc: 0.9569 - val_loss: 0.2473 - val_acc: 0.9538
Epoch 20/100
- 0s - loss: 0.2569 - acc: 0.9591 - val_loss: 0.2451 - val_acc: 0.9614
Epoch 21/100
- 0s - loss: 0.2464 - acc: 0.9614 - val_loss: 0.2402 - val_acc: 0.9625
Epoch 22/100
- 0s - loss: 0.2470 - acc: 0.9598 - val_loss: 0.2453 - val_acc: 0.9538
Epoch 23/100
- 0s - loss: 0.2498 - acc: 0.9601 - val_loss: 0.2408 - val_acc: 0.9538
Epoch 24/100
- 0s - loss: 0.2433 - acc: 0.9587 - val_loss: 0.2421 - val_acc: 0.9505
Epoch 25/100
- 0s - loss: 0.2406 - acc: 0.9613 - val_loss: 0.2307 - val_acc: 0.9538
Epoch 26/100
- 0s - loss: 0.2372 - acc: 0.9601 - val_loss: 0.2301 - val_acc: 0.9538
Epoch 27/100
- 0s - loss: 0.2294 - acc: 0.9615 - val_loss: 0.2287 - val_acc: 0.9598
Epoch 28/100
- 0s - loss: 0.2349 - acc: 0.9613 - val_loss: 0.2255 - val_acc: 0.9571
Epoch 29/100
- 0s - loss: 0.2326 - acc: 0.9579 - val_loss: 0.2206 - val_acc: 0.9554
Epoch 30/100
- 0s - loss: 0.2257 - acc: 0.9614 - val_loss: 0.2180 - val_acc: 0.9571
Epoch 31/100
- 0s - loss: 0.2258 - acc: 0.9618 - val_loss: 0.2200 - val_acc: 0.9609
Epoch 32/100
- 0s - loss: 0.2236 - acc: 0.9611 - val_loss: 0.2213 - val_acc: 0.9538
Epoch 33/100
- 0s - loss: 0.2201 - acc: 0.9622 - val_loss: 0.2112 - val_acc: 0.9587
Epoch 34/100
- 0s - loss: 0.2253 - acc: 0.9617 - val_loss: 0.2159 - val_acc: 0.9549
Epoch 35/100
- 0s - loss: 0.2207 - acc: 0.9629 - val_loss: 0.2114 - val_acc: 0.9598
Epoch 36/100
- 0s - loss: 0.2228 - acc: 0.9606 - val_loss: 0.2136 - val_acc: 0.9592
Epoch 37/100
- 0s - loss: 0.2163 - acc: 0.9617 - val_loss: 0.2098 - val_acc: 0.9620
Epoch 38/100
- 0s - loss: 0.2167 - acc: 0.9621 - val_loss: 0.2179 - val_acc: 0.9560
Epoch 39/100
- 0s - loss: 0.2137 - acc: 0.9611 - val_loss: 0.2120 - val_acc: 0.9576
Epoch 40/100
- 0s - loss: 0.2093 - acc: 0.9636 - val_loss: 0.2003 - val_acc: 0.9658
Epoch 41/100
- 0s - loss: 0.2155 - acc: 0.9621 - val_loss: 0.2016 - val_acc: 0.9625
Epoch 42/100
- 0s - loss: 0.2076 - acc: 0.9652 - val_loss: 0.1994 - val_acc: 0.9598
Epoch 43/100
- 0s - loss: 0.2128 - acc: 0.9626 - val_loss: 0.2053 - val_acc: 0.9587
Epoch 44/100
- 0s - loss: 0.2071 - acc: 0.9643 - val_loss: 0.1974 - val_acc: 0.9630
Epoch 45/100
- 0s - loss: 0.2078 - acc: 0.9637 - val_loss: 0.2047 - val_acc: 0.9592
Epoch 46/100
- 0s - loss: 0.2130 - acc: 0.9615 - val_loss: 0.2089 - val_acc: 0.9538
Epoch 47/100
- 0s - loss: 0.2113 - acc: 0.9617 - val_loss: 0.2007 - val_acc: 0.9582
Epoch 48/100
- 0s - loss: 0.2072 - acc: 0.9656 - val_loss: 0.2026 - val_acc: 0.9538
Epoch 49/100
- 0s - loss: 0.2055 - acc: 0.9636 - val_loss: 0.2013 - val_acc: 0.9565
Epoch 50/100
- 0s - loss: 0.2089 - acc: 0.9610 - val_loss: 0.1974 - val_acc: 0.9582
Epoch 51/100
- 0s - loss: 0.2033 - acc: 0.9632 - val_loss: 0.1946 - val_acc: 0.9587
Epoch 52/100
- 0s - loss: 0.2075 - acc: 0.9626 - val_loss: 0.1995 - val_acc: 0.9625
Epoch 53/100
- 0s - loss: 0.2030 - acc: 0.9635 - val_loss: 0.1948 - val_acc: 0.9603
Epoch 54/100
- 0s - loss: 0.2038 - acc: 0.9641 - val_loss: 0.1939 - val_acc: 0.9679
Epoch 55/100
- 0s - loss: 0.2048 - acc: 0.9636 - val_loss: 0.1950 - val_acc: 0.9592
Epoch 56/100
- 0s - loss: 0.2037 - acc: 0.9637 - val_loss: 0.1917 - val_acc: 0.9636
Epoch 57/100
- 0s - loss: 0.2014 - acc: 0.9647 - val_loss: 0.1909 - val_acc: 0.9620
Epoch 58/100
- 0s - loss: 0.1979 - acc: 0.9651 - val_loss: 0.1896 - val_acc: 0.9614
Epoch 59/100
- 0s - loss: 0.2068 - acc: 0.9629 - val_loss: 0.1909 - val_acc: 0.9609
Epoch 60/100
- 0s - loss: 0.1990 - acc: 0.9633 - val_loss: 0.1908 - val_acc: 0.9614
Epoch 61/100
- 0s - loss: 0.1921 - acc: 0.9666 - val_loss: 0.1904 - val_acc: 0.9620
Epoch 62/100
- 0s - loss: 0.2018 - acc: 0.9629 - val_loss: 0.1896 - val_acc: 0.9614
Epoch 63/100
- 0s - loss: 0.2041 - acc: 0.9620 - val_loss: 0.1917 - val_acc: 0.9625
Epoch 64/100
- 0s - loss: 0.2000 - acc: 0.9652 - val_loss: 0.1891 - val_acc: 0.9620
Epoch 65/100
- 0s - loss: 0.1967 - acc: 0.9656 - val_loss: 0.1916 - val_acc: 0.9609
Epoch 66/100
- 0s - loss: 0.1961 - acc: 0.9639 - val_loss: 0.1854 - val_acc: 0.9641
Epoch 67/100
- 0s - loss: 0.1969 - acc: 0.9648 - val_loss: 0.1887 - val_acc: 0.9592
Epoch 68/100
- 0s - loss: 0.1990 - acc: 0.9630 - val_loss: 0.1874 - val_acc: 0.9636
Epoch 69/100
- 0s - loss: 0.1923 - acc: 0.9662 - val_loss: 0.1893 - val_acc: 0.9614
Epoch 70/100
- 0s - loss: 0.1925 - acc: 0.9645 - val_loss: 0.1853 - val_acc: 0.9641
Epoch 71/100
- 0s - loss: 0.1948 - acc: 0.9622 - val_loss: 0.1905 - val_acc: 0.9592
Epoch 72/100
- 0s - loss: 0.1994 - acc: 0.9628 - val_loss: 0.1852 - val_acc: 0.9641
Epoch 73/100
- 0s - loss: 0.1953 - acc: 0.9651 - val_loss: 0.1834 - val_acc: 0.9641
Epoch 74/100
- 0s - loss: 0.1888 - acc: 0.9670 - val_loss: 0.1816 - val_acc: 0.9620
Epoch 75/100
- 0s - loss: 0.1933 - acc: 0.9659 - val_loss: 0.1860 - val_acc: 0.9620
Epoch 76/100
- 0s - loss: 0.1917 - acc: 0.9635 - val_loss: 0.1828 - val_acc: 0.9625
Epoch 77/100
- 0s - loss: 0.1907 - acc: 0.9677 - val_loss: 0.1828 - val_acc: 0.9603
Epoch 78/100
- 0s - loss: 0.1990 - acc: 0.9637 - val_loss: 0.1805 - val_acc: 0.9652
Epoch 79/100
- 0s - loss: 0.1934 - acc: 0.9652 - val_loss: 0.1864 - val_acc: 0.9614
Epoch 80/100
- 0s - loss: 0.1870 - acc: 0.9667 - val_loss: 0.1808 - val_acc: 0.9674
Epoch 81/100
- 0s - loss: 0.1901 - acc: 0.9660 - val_loss: 0.1825 - val_acc: 0.9625
Epoch 82/100
- 0s - loss: 0.1880 - acc: 0.9649 - val_loss: 0.1871 - val_acc: 0.9663
Epoch 83/100
- 0s - loss: 0.1901 - acc: 0.9677 - val_loss: 0.1808 - val_acc: 0.9620
Epoch 84/100
- 0s - loss: 0.1941 - acc: 0.9620 - val_loss: 0.1853 - val_acc: 0.9647
Epoch 85/100
- 0s - loss: 0.1867 - acc: 0.9674 - val_loss: 0.1825 - val_acc: 0.9620
Epoch 86/100
- 0s - loss: 0.1940 - acc: 0.9651 - val_loss: 0.1877 - val_acc: 0.9576
Epoch 87/100
- 0s - loss: 0.1913 - acc: 0.9633 - val_loss: 0.1817 - val_acc: 0.9620
Epoch 88/100
- 0s - loss: 0.1940 - acc: 0.9649 - val_loss: 0.1834 - val_acc: 0.9636
Epoch 89/100
- 0s - loss: 0.1886 - acc: 0.9656 - val_loss: 0.1844 - val_acc: 0.9625
Epoch 90/100
- 0s - loss: 0.1835 - acc: 0.9677 - val_loss: 0.1899 - val_acc: 0.9641
Epoch 91/100
- 0s - loss: 0.1884 - acc: 0.9674 - val_loss: 0.1894 - val_acc: 0.9587
Epoch 92/100
- 0s - loss: 0.1855 - acc: 0.9675 - val_loss: 0.1894 - val_acc: 0.9582
Epoch 93/100
- 0s - loss: 0.1864 - acc: 0.9655 - val_loss: 0.1808 - val_acc: 0.9641
Epoch 94/100
- 0s - loss: 0.1878 - acc: 0.9671 - val_loss: 0.1865 - val_acc: 0.9609
Epoch 95/100
- 0s - loss: 0.1901 - acc: 0.9662 - val_loss: 0.1859 - val_acc: 0.9641
Epoch 96/100
- 0s - loss: 0.1836 - acc: 0.9670 - val_loss: 0.1823 - val_acc: 0.9647
Epoch 97/100
- 0s - loss: 0.1876 - acc: 0.9664 - val_loss: 0.1799 - val_acc: 0.9668
Epoch 98/100
- 0s - loss: 0.1854 - acc: 0.9675 - val_loss: 0.1912 - val_acc: 0.9565
Epoch 99/100
- 0s - loss: 0.1881 - acc: 0.9673 - val_loss: 0.1801 - val_acc: 0.9668
Epoch 100/100
- 0s - loss: 0.1821 - acc: 0.9674 - val_loss: 0.1758 - val_acc: 0.9701
内容和代码分别整理于:
[1]: 脑电信号同步分析及癫痫发作预测方法研究
[2]: http://dy.163.com/v2/article/detail/EEC68EH5054281P3.html
参考
利用深度学习(Keras)进行癫痫分类-Python案例
本文章由脑机学习者Rose笔记分享,QQ交流群:903290195
更多分享,请关注公众号




