HihoCoder - 1175 拓扑排序·二
描述
小Hi和小Ho所在学校的校园网被黑客入侵并投放了病毒。这事在校内BBS上立刻引起了大家的讨论，当然小Hi和小Ho也参与到了其中。从大家各自了解的情况中，小Hi和小Ho整理得到了以下的信息：
- 校园网主干是由N个节点(编号1..N)组成，这些节点之间有一些单向的网路连接。若存在一条网路连接(u,v)链接了节点u和节点v，则节点u可以向节点v发送信息，但是节点v不能通过该链接向节点u发送信息。
- 在刚感染病毒时，校园网立刻切断了一些网络链接，恰好使得剩下网络连接不存在环，避免了节点被反复感染。也就是说从节点i扩散出的病毒，一定不会再回到节点i。
- 当1个病毒感染了节点后，它并不会检查这个节点是否被感染，而是直接将自身的拷贝向所有邻居节点发送，它自身则会留在当前节点。所以一个节点有可能存在多个病毒。
- 现在已经知道黑客在一开始在K个节点上分别投放了一个病毒。
举个例子，假设切断部分网络连接后学校网络如下图所示，由4个节点和4条链接构成。最开始只有节点1上有病毒。
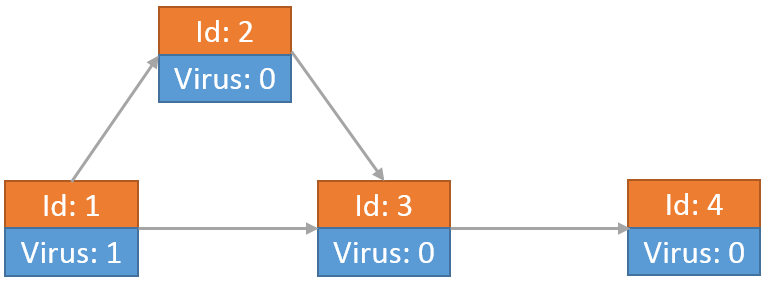
最开始节点1向节点2和节点3传送了病毒，自身留有1个病毒：
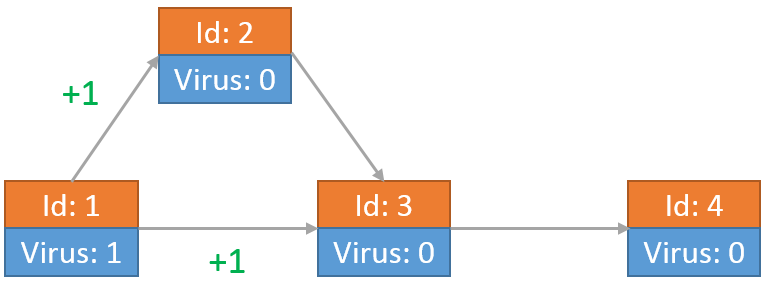
其中一个病毒到达节点2后，向节点3传送了一个病毒。另一个到达节点3的病毒向节点4发送自己的拷贝：
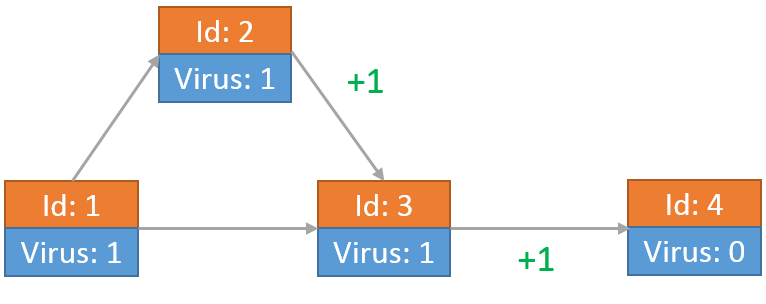
当从节点2传送到节点3的病毒到达之后，该病毒又发送了一份自己的拷贝向节点4。此时节点3上留有2个病毒：
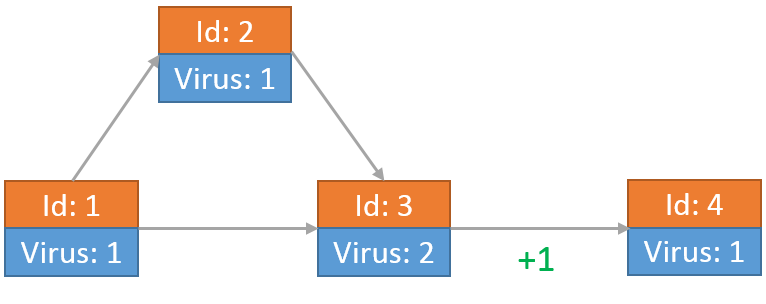
最后每个节点上的病毒为：
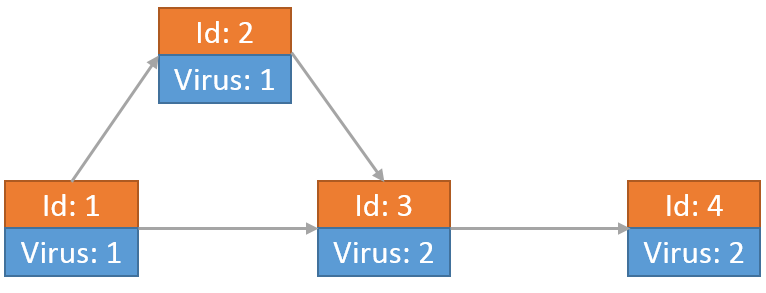
小Hi和小Ho根据目前的情况发现一段时间之后，所有的节点病毒数量一定不会再发生变化。那么对于整个网络来说，最后会有多少个病毒呢？
输入
第1行：3个整数N,M,K，1≤K≤N≤100,000，1≤M≤500,000
第2行：K个整数A[i]，A[i]表示黑客在节点A[i]上放了1个病毒。1≤A[i]≤N
第3..M+2行：每行2个整数 u,v，表示存在一条从节点u到节点v的网络链接。数据保证为无环图。1≤u,v≤N
输出
第1行：1个整数，表示最后整个网络的病毒数量 MOD 142857
样例输入
4 4 1 1 1 2 1 3 2 3 3 4
样例输出
6
思路：一开始没看清题，这道题说的是整个网络。后来我习惯性把num清零，可是发现这样做会wa，原来这道题要求的是之前的网络和现在的网络（总网络）的病毒数量。
#include <bits/stdc++.h> using namespace std; #define ll long long vector<int>to[100000+8]; queue<int>q; int n, m, k, num[100000+8], point, du[100000+8], number; void get() { number = 0; while(!q.empty()) { int t = q.front(); q.pop(); number += num[t]; number %= 142857; for(int i = 0; i<to[t].size(); i++) { num[to[t][i]] += num[t]; num[to[t][i]] %= 142857; du[to[t][i]]--; if(!du[to[t][i]]) q.push(to[t][i]); } } } int main() { int a, b; while(scanf("%d%d%d", &n, &m, &k) != EOF) { // memset(num, 0, sizeof(num)); memset(du, 0, sizeof(du)); for(int i = 0; i <= n; i++) if(to[i].size()) to[i].clear(); while(!q.empty())q.pop(); for(int i = 0; i<k; i++) { scanf("%d", &point); num[point]++; } for(int i = 0; i<m; i++) { scanf("%d%d", &a, &b); to[a].push_back(b); du[b]++; } for(int i = 1; i <= n; i++) if(!du[i]) q.push(i); get(); printf("%d\n", number); } return 0; } /* 5 5 2 2 4 1 2 1 4 2 3 4 3 3 5 */
