线段树算法笔记

 

 【例题】

一、单点更新

 [HDU-1166] 

#include<cstdio>
#include<string>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<cstring>
#include<set>
#include<queue>
#include<algorithm>
#include<vector>
#include<map>
#include<cctype>
#include<stack>
#include<sstream>
#include<list>
#include<assert.h>
#include<bitset>
#include<numeric>
#define debug() puts("++++")
#define gcd(a,b) __gcd(a,b)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a,b,sizeof(a))
#define sz size()
#define be begin()
#define pu push_up
#define pd push_down
#define cl clear()
#define mdzz int mid=(l+r)>>1;
#define lowbit(x) -x&x
#define all 1,n,1
#define rep(i,x,n) for(int i=(x); i<(n); i++)
#define in freopen("in.in","r",stdin)
#define out freopen("out.out","w",stdout)
using namespace std;
typedef long long ll;
typedef unsigned long long ULL;
typedef pair<int,int> P;
const int INF = 0x3f3f3f3f;
const ll LNF = 1e18;
const int maxn = 200010 + 20;
const int maxm = 1e6 + 10;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int dx[] = {-1,1,0,0,1,1,-1,-1};
const int dy[] = {0,0,1,-1,1,-1,1,-1};
int dir[4][2] = {{0,1},{0,-1},{-1,0},{1,0}};
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int n,m,t;
int x,y,op;
ll a[maxn];
/*
给定两个操作，一个对区间所有元素加1，一个询问区间能被3整除的数有多少个
*/
ll sum[maxn<<2],add[maxn<<2];
void pushup(int rt)
{
    sum[rt]=sum[rt<<1]+sum[rt<<1|1]; //区间查询和
}

void build(int l,int r,int rt)
{
    add[rt]=0;
    if(l==r)
    {
        scanf("%lld",&sum[rt]);
        return ;
    }
    mdzz
    build(lson);
    build(rson);
    pushup(rt);
}
void update(int p,int val,int l,int r,int rt) //点p更新了val
{
    if(l==r) //
    {
        sum[rt] += val;
        return ;
    }
    mdzz
    if(p<=mid) update(p,val,lson); //
    else update(p,val,rson); //
    pushup(rt);
}
ll query(int L,int R,int l,int r,int rt)
{
    if(L<=l&&R>=r) return sum[rt];
    mdzz
    ll res=0;
    if(L<=mid) res += query(L,R,lson);
    if(R>mid) res += query(L,R,rson);
    return res;
}

int main()
{
    char op[15];
    scanf("%d",&t);
    for(int ca=1;ca<=t;ca++)
    {
        scanf("%d",&n);
        build(1,n,1);
        printf("Case %d:\n",ca);
        while(~scanf("%s",op))
        {
            if(op[0]=='Q')
            {
                scanf("%d%d",&x,&y);
                printf("%lld\n",query(x,y,1,n,1));
            }
            else if(op[0]=='A')
            {
                scanf("%d%d",&x,&y);
                update(x,y,1,n,1);
            }
            else if(op[0]=='S')
            {
                scanf("%d%d",&x,&y);
                update(x,-y,1,n,1);
            }
            else break;
        }
    }
}

/*
【题意】
add i j:单点更新-点i加j
sub i j:单点更新-点i减j
query i j:区间查询-[i,j]之和

【类型】线段树单点更新、区间求和


【分析】模板


【时间复杂度&&优化】


【trick】


【数据】
*/







/*
void pushdown(int rt,int m)
{
    if(cover[rt]>=0)
    {
        //区间覆盖
        cover[rt<<1] = cover[rt<<1|1] = cover[rt];
        sum[rt<<1] = cover[rt]*(m-(m>>1));
        sum[rt<<1|1] = cover[rt]*(m>>1);
        add[rt<<1] = add[rt<<1|1] =  0;     //set操作中取消add
        cover[rt] = -1;
    }
    if(add[rt])
    {
        //区间求和
        add[rt<<1]   += add[rt];
        add[rt<<1|1] += add[rt];
        sum[rt<<1] += add[rt]*(m-(m>>1));
        sum[rt<<1|1] += add[rt]*(m>>1);
        add[rt]=0;
    }
}
*/

 

 HDU - 1754 

#include<cstdio>
#include<string>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<cstring>
#include<set>
#include<queue>
#include<algorithm>
#include<vector>
#include<map>
#include<cctype>
#include<stack>
#include<sstream>
#include<list>
#include<assert.h>
#include<bitset>
#include<numeric>
#define debug() puts("++++")
#define gcd(a,b) __gcd(a,b)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a,b,sizeof(a))
#define sz size()
#define be begin()
#define pu push_up
#define pd push_down
#define cl clear()
#define mdzz int mid=(l+r)>>1;
#define lowbit(x) -x&x
#define all 1,n,1
#define rep(i,x,n) for(int i=(x); i<(n); i++)
#define in freopen("in.in","r",stdin)
#define out freopen("out.out","w",stdout)
using namespace std;
typedef long long ll;
typedef unsigned long long ULL;
typedef pair<int,int> P;
const int INF = 0x3f3f3f3f;
const ll LNF = 1e18;
const int maxn = 200010 + 20;
const int maxm = 1e6 + 10;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int dx[] = {-1,1,0,0,1,1,-1,-1};
const int dy[] = {0,0,1,-1,1,-1,1,-1};
int dir[4][2] = {{0,1},{0,-1},{-1,0},{1,0}};
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int n,m,t;
ll max(ll x,ll y)
{
    if(x>y) return x;
    else return y;
}
ll sum[maxn<<2],add[maxn<<2];
void pushup(int rt)
{
    sum[rt]=max(sum[rt<<1],sum[rt<<1|1]); //区间查询和
}
void build(int l,int r,int rt)
{
    if(l==r)
    {
        scanf("%lld", &sum[rt]);
        return ;
    }
    mdzz
    build(lson);
    build(rson);
    pushup(rt);
}
void update(int p,int val,int l,int r,int rt) //点p更新了val
{
    if(l==r) //
    {
        sum[rt] = val;
        return ;
    }
    mdzz
    if(p <= mid) update(p,val,lson); //
    else update(p,val,rson);         //
    pushup(rt);
}
ll query(int L,int R,int l,int r,int rt)
{
    if(L<=l&&R>=r) return sum[rt];
    mdzz
    ll res=0;
    if(L<=mid) res = max(res,query(L,R,lson));
    if(R>mid) res = max(res,query(L,R,rson));
    return res;
}

int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        build(1,n,1);
        while(m--)
        {
            char op[3];int x,y;
            scanf("%s%d%d",op,&x,&y);
            if(op[0]=='Q')
                printf("%lld\n",query(x,y,1,n,1));
            else update(x,y,1,n,1);
        }
    }
}

/*
【题意】
U i j:单点覆盖-点i改为j
Q i j:区间查询-查询最值

【类型】线段树单点更新、区间求和


【分析】模板


【时间复杂度&&优化】


【trick】


【数据】
*/







/*
void pushdown(int rt,int m)
{
    if(cover[rt]>=0)
    {
        //区间覆盖
        cover[rt<<1] = cover[rt<<1|1] = cover[rt];
        sum[rt<<1] = cover[rt]*(m-(m>>1));
        sum[rt<<1|1] = cover[rt]*(m>>1);
        add[rt<<1] = add[rt<<1|1] =  0;     //set操作中取消add
        cover[rt] = -1;
    }
    if(add[rt])
    {
        //区间求和
        add[rt<<1]   += add[rt];
        add[rt<<1|1] += add[rt];
        sum[rt<<1] += add[rt]*(m-(m>>1));
        sum[rt<<1|1] += add[rt]*(m>>1);
        add[rt]=0;
    }
}
*/

 

 HDU - 1394【最小循环逆序数-权值线段树】

#include<cstdio>
#include<string>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<cstring>
#include<set>
#include<queue>
#include<algorithm>
#include<vector>
#include<map>
#include<cctype>
#include<stack>
#include<sstream>
#include<list>
#include<assert.h>
#include<bitset>
#include<numeric>
#define debug() puts("++++")
#define gcd(a,b) __gcd(a,b)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a,b,sizeof(a))
#define sz size()
#define be begin()
#define pu push_up
#define pd push_down
#define cl clear()
#define mdzz int mid=(l+r)>>1;
#define lowbit(x) -x&x
#define all 1,n,1
#define rep(i,x,n) for(int i=(x); i<(n); i++)
#define in freopen("in.in","r",stdin)
#define out freopen("out.out","w",stdout)
using namespace std;
typedef long long ll;
typedef unsigned long long ULL;
typedef pair<int,int> P;
const int INF = 0x3f3f3f3f;
const ll LNF = 1e18;
const int maxn = 200010 + 20;
const int maxm = 1e6 + 10;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int dx[] = {-1,1,0,0,1,1,-1,-1};
const int dy[] = {0,0,1,-1,1,-1,1,-1};
int dir[4][2] = {{0,1},{0,-1},{-1,0},{1,0}};
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int n,m,t;
ll sum[maxn<<2];
int a[maxn<<2];
void pushup(int rt)
{
    sum[rt]=sum[rt<<1]+sum[rt<<1|1]; //区间查询
}
void build(int l,int r,int rt)
{
    sum[rt]=0;
    if(l==r) return;
    mdzz
    build(lson);
    build(rson);
    //pushup(rt);
}
void update(int p,int l,int r,int rt) //点p更新
{
    if(l==r) //
    {
        sum[rt]++;   //叶子节点
        return ;
    }
    mdzz
    if(p <= mid) update(p,lson); //
    else update(p,rson);         //
    pushup(rt);
}
ll query(int L,int R,int l,int r,int rt)
{
    if(L<=l&&R>=r) return sum[rt];
    mdzz
    ll res=0;
    if(L<=mid) res += query(L,R,lson);
    if(R>mid) res += query(L,R,rson);
    return res;
}

int main()
{
    while(~scanf("%d",&n))
    {
        build(0,n-1,1);
        int s=0;
        for(int i=0;i<n;i++)
        {
            scanf("%d",&a[i]);
            s += query(a[i],n-1,0,n-1,1);
            update(a[i],0,n-1,1);
        }
        int ret=s;
        for(int i=0;i<n;i++)
        {
            s+=n-a[i]-1-a[i];
            ret = min(ret,s);
        }
        printf("%d\n",ret);
    }
}

/*
【题意】线段树求逆序数

【类型】线段树区间求和

【分析】模板

【时间复杂度&&优化】

【trick】

【数据】
*/

 

 

 POJ - 2299    Ultra-QuickSort 【离散化/逆序对/权值线段树】

#include<cstdio>
#include<string>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<cstring>
#include<set>
#include<queue>
#include<algorithm>
#include<vector>
#include<map>
#include<cctype>
#include<stack>
#include<sstream>
#include<list>
#include<assert.h>
#include<bitset>
#include<numeric>
#define debug() puts("++++")
#define gcd(a,b) __gcd(a,b)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a,b,sizeof(a))
#define be begin()
#define pu push_up
#define pd push_down
#define cl clear()
#define mdzz int mid=(l+r)>>1;
#define lowbit(x) -x&x
#define all 1,n,1
#define rep(i,x,n) for(int i=(x); i<(n); i++)
#define in freopen("in.in","r",stdin)
#define out freopen("out.out","w",stdout)
using namespace std;
typedef long long ll;
typedef unsigned long long ULL;
typedef pair<int,int> P;
const int INF = 0x3f3f3f3f;
const ll LNF = 1e18;
const int maxn = 500000 + 20;
const int maxm = 1e6 + 10;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int dx[] = {-1,1,0,0,1,1,-1,-1};
const int dy[] = {0,0,1,-1,1,-1,1,-1};
int dir[4][2] = {{0,1},{0,-1},{-1,0},{1,0}};
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int n,m,t;
int sz;
ll sum[maxn<<2];
int a[maxn],id[maxn];
bool cmp(int a,int b){return a>b;}
void pushup(int rt)
{
    sum[rt]=sum[rt<<1]+sum[rt<<1|1]; //区间查询
}
void build(int l,int r,int rt)
{
    sum[rt]=0;
    if(l==r) return;
    mdzz
    build(lson);
    build(rson);
    //pushup(rt);
}
void update(int p,int l,int r,int rt) //点p更新
{
    if(l==r)
    {
        sum[rt]++;   //叶子节点
        return ;
    }
    mdzz
    if(p<=mid) update(p,lson); //
    else update(p,rson);         //
    pushup(rt);
}
ll query(int L,int R,int l,int r,int rt)
{
    if(L<=l && R>=r) return sum[rt];
    mdzz
    ll res=0;
    if(L<=mid) res += query(L,R,lson);
    if(R>mid)  res += query(L,R,rson);
    return res;
}
void init()
{
    //int sz;
    for(int i=0;i<=n*4;i++)
        sum[i]=0;
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]), id[i]=a[i];
    sort(id+1,id+n+1), sz=unique(id+1,id+n+1)-id; //离散化
    for(int i=1;i<=n;i++)
        a[i]=lower_bound(id+1,id+sz,a[i])-id; //映射
}
void solve()
{
    ll ans=0;
    for(int i=1;i<=n;i++)
    {
        ans += query(a[i],n,1,n,1);
        update(a[i],1,n,1);
    }
    printf("%lld\n",ans);
}
int main()
{
    while(~scanf("%d",&n),n)
    {
        init(),solve();
    }
}
/*
5
9 1 0 5 4
3
1 2 3
0
*/

 

 HDU - 2795【巧妙建模线段树，单点更新最大值】

#include<cstdio>
#include<string>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<cstring>
#include<set>
#include<queue>
#include<algorithm>
#include<vector>
#include<map>
#include<cctype>
#include<stack>
#include<sstream>
#include<list>
#include<assert.h>
#include<bitset>
#include<numeric>
#define debug() puts("++++")
#define gcd(a,b) __gcd(a,b)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a,b,sizeof(a))
#define sz size()
#define be begin()
#define pu push_up
#define pd push_down
#define cl clear()
#define mdzz int mid=(l+r)>>1;
#define lowbit(x) -x&x
#define all 1,n,1
#define rep(i,x,n) for(int i=(x); i<(n); i++)
#define in freopen("in.in","r",stdin)
#define out freopen("out.out","w",stdout)
using namespace std;
typedef long long ll;
typedef unsigned long long ULL;
typedef pair<int,int> P;
const int INF = 0x3f3f3f3f;
const ll LNF = 1e18;
const int maxn = 200010 + 20;
const int maxm = 1e6 + 10;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int dx[] = {-1,1,0,0,1,1,-1,-1};
const int dy[] = {0,0,1,-1,1,-1,1,-1};
int dir[4][2] = {{0,1},{0,-1},{-1,0},{1,0}};
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
int n,m,h,t,w;
ll sum[maxn<<2];
int a[maxn<<2];
void pushup(int rt)
{
    sum[rt]=max(sum[rt<<1],sum[rt<<1|1]); //区间查询
}
void build(int w,int l,int r,int rt)
{
    sum[rt]=w; //每条的宽度定下来,用数组存起来,初始化为w
    if(l==r) return;
    mdzz
    build(w,lson);
    build(w,rson);
    //pushup(rt);
}

ll query(int w,int l,int r,int rt)
{
    if(l==r) //只需要每次找到的时候把节点值减掉，广告需要占用的长度就行
    {
        sum[rt]-=w;//点修改在查询中顺便完成了,该层宽度减少
        return l;
    }
    mdzz
    ll res=0;
    //线段树中的节点保存最大的剩余空间。怎么在最前面呢，如果左儿子的最大剩余空间存在，优先访问左儿子(从上到下的广告牌剩余空间在线段树中对应的位置依次从左到右）
    if(sum[rt<<1] >= w) res = query(w,lson); //当海报宽度小于树的左边区域宽度时，说明左边是可以贴海报的
    else res = query(w,rson);
    pushup(rt); //有过修改必须在回溯中维护节点内容,左右子树里能放的最大长度存入父亲节点，进行更新
    return res;
}

int main()
{
    while(~scanf("%d%d%d",&h,&w,&n))
    {
        if(h>n) h=n;
        build(w,1,h,1);
        while(n--)
        {
            int x;
            scanf("%d",&x);
            if(sum[1]<x) puts("-1");
            else printf("%lld\n",query(x,1,h,1)); //如果这个公告没有超出公告板的长度，那么才能放入
        }
    }
}

/*
【题意】每张广告都是高度为1宽度为wi的细长的矩形纸条。贴广告的人总是会优先选择最上面的位置来帖，而且在所有最上面的可能位置中，他会选择最左面的位置，而且不能把已经贴好的广告盖住。 如果没有合适的位置了，那么这张广告就不会被贴了。 现在已知广告牌的尺寸和每张广告的尺寸，求每张广告被贴在的行编号。

【类型】维护区间剩余长度的最大值

【分析】把每一条边当作树的节点，把每条边剩余的长度的最大值用数组维护优先处理最上面的节点

【时间复杂度&&优化】

【trick】这道题很难想到是用线段树，确实转化的很巧妙。把展板旋转九十度，从1到min(h,n)的一行，用每个变量来存下面每一行的长度w，构造线段树，节点上保存下面的长度的最大值。更新的时候就减去相应节点的wi，然后返回那个节点的L或者R，就是应该贴在的那一行。

【数据】
*/

 

 

 

线段树的优点:
  O(logn)时间内，在一段区间中求最大最小值

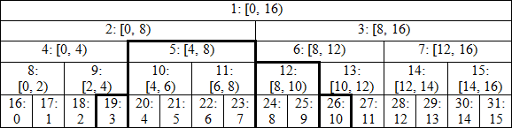
线段树的特征:

• 二叉树

 

• 每个节点表示一个区间的最大值

 

• 左儿子 = 平分后左区间，右儿子 = 平分后右区间

 

• 不可增减节点(线段数结点总数需要在最开始就给定)

 

• 空间复杂度: O(n)

 

线段树的操作:

线段树的查询: O(logn)

• 查询的区间 和 线段树节点区间 相等 -> 直接返回

 

• 查询的区间 被 线段树节点区间 包含-> 递归向下搜索左右子树

 

• 查询的区间 和 线段树节点区间 不相交 -> 结束

 

• 查询的区间 和 线段树节点区间 相交且不相等 -> 分裂查询区间

 

线段树的建立: O(n)

• 自上而下递归分裂

 

• 自下而上回溯更新

 

线段树的更新: O(logn)

• 自上而下递归查询

 

• 自下而上回溯更新

 

问题特征:

• 对区间求sum

 

• 对区间求Max/Min

 

• 对区间求Count

构建形式

1. 下标作为建立区间
2. 值作为建立区间

【参考】：

http://codeforces.com/blog/entry/18051