KMP算法笔记
【简述】:
kmp算法:
1 kmp是用来匹配字符串,只能够匹配单一的字符串
2 kmp的算法的过程:
1:假设文本串的长度为n,模式串的长度为m;
2:先例用O(m)的时间去预处理next数组,next数组的意思指的是当前的字符串匹配失败后要转到的下一个状态;
3:利用o(n)的时间去完成匹配;
3 时间复杂度为o(n+m)即o(n);
【例题】:
1. 可重叠匹配:j=nxt[j]
求模式串在主串中出现的次数,可重叠【HDU 1686 Oulipo】

#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <vector> #include <queue> #include <stack> #include <set> #include <map> #include <string> #include <cmath> #include <cstdlib> #include <deque> #include <ctime> #define fst first #define sec second #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 #define ms(a,x) memset(a,x,sizeof(a)) typedef long long LL; #define pi pair < int ,int > #define MP make_pair using namespace std; const double eps = 1E-8; const int dx4[4]={1,0,0,-1}; const int dy4[4]={0,-1,1,0}; const int inf = 0x3f3f3f3f; const int N=1E4+7; string a,b; int ans; int nxt[N]; void getnxt( int n) { int i = 0; int j = -1; nxt[0] = -1; while (i<n) if (j==-1||b[i]==b[j]) nxt[++i]=++j; else j = nxt[j]; } void kmp( int n,int m) { int i = 0 ; int j = 0 ; getnxt(m); // for ( int i = 0 ; i < m ; i++) cout<<i<<" "<<nxt[i]<<endl; while (i<n) { if (j==-1||a[i]==b[j]) i++,j++; else j = nxt[j]; if (j==m) ans++,j=nxt[j]; } } int main() { ios::sync_with_stdio(false); int T; cin>>T; while (T--) { cin>>a>>b; swap(a,b); int la = a.length(); int lb = b.length(); ans = 0 ; kmp(la,lb); cout<<ans<<endl; } return 0; }
2. 不可重叠匹配:j=0
问模式串在文本串中出现的次数,不允许重叠【HDU 2087 剪花布条】
//不是j=nxt[j],因为不能重复,只要每次找到的时候j=0一下就好。

#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <vector> #include <queue> #include <stack> #include <set> #include <map> #include <string> #include <cmath> #include <cstdlib> #include <deque> #include <ctime> #define fst first #define sec second #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 #define ms(a,x) memset(a,x,sizeof(a)) typedef long long LL; #define pi pair < int ,int > #define MP make_pair using namespace std; const double eps = 1E-8; const int dx4[4]={1,0,0,-1}; const int dy4[4]={0,-1,1,0}; const int inf = 0x3f3f3f3f; const int N=1E4+7; string a,b; int ans; int nxt[N]; void getnxt( int n) { int i = 0; int j = -1; nxt[0] = -1; while (i<n) if (j==-1||b[i]==b[j]) nxt[++i]=++j; else j = nxt[j]; } void kmp( int n,int m) { int i = 0 ; int j = 0 ; ans=0; getnxt(m); // for ( int i = 0 ; i < m ; i++) cout<<i<<" "<<nxt[i]<<endl; while (i<n) { if (j==-1||a[i]==b[j]) i++,j++; else j = nxt[j]; if (j==m) ans++,j=0; } } int main() { ios::sync_with_stdio(false); while(cin>>a>>b) { ans=0; if(a[0]=='#'||b[0]=='#') break; int len1=a.size(); int len2=b.size(); kmp(len1,len2); printf("%d\n",ans); } return 0; }
3. KMP找子串第一次出现的位置

#include<stdio.h> #include<string.h> #define N 1000005 int next[N],a[N],b[N]; int m,n; void Next()//就是上面的分匹配表的实现 { int i,j; i=0; j=-1; next[i]=j; //匹配表初值 while(i<m) { if(j==-1||b[i]==b[j]) { i++; j++; next[i]=j; } else j=next[j]; } return ; } int KMP()//kmp匹配算法 { int i,j; i=j=0; Next();//先计算部分匹配表 while(i<n) { if(j==-1||a[i]==b[j]) { i++; j++; if(j==m) return i-m+1;//找到目标字符串,返回到主程序。 } else j=next[j];//a[i]与b[j]不匹配,查表需要跳过的字符个数。 } return -1;//没有找到返回-1 } int main() { int t; scanf("%d",&t); while(t--) { scanf("%d%d",&n,&m); for(int i=0; i<n; i++) scanf("%d",&a[i]); for(int i=0; i<m; i++) scanf("%d",&b[i]); printf("%d\n",KMP()); } return 0; }
【题目总结】:
1.求匹配串在文本串出现的次数
直接利用第二种写法即可。
题目:HDU - 1686
2.求匹配串在文本串第一次匹配成功时的起始位置。
套用第一种写法即可。
题目:HDU - 1711
3. 给定一个字符串,问我们还需要添加几个字符可以构成一个由n个循环节组成的字符串。
利用Next数组的性质,
- 假设字符串的长度为len,那么最小的循环节就是cir = len-next[len] ;
- 如果有len%cir == 0,那么这个字符串就是已经是完美的字符串,不用添加任何字符;
- 如果不是完美的那么需要添加的字符数就是cir - (len-(len/cir)*cir)),相当与需要在最后一个循环节上面添加几个。
题目:HDU - 3746
4.给你一个字符串s求出所有满足s[i] == s[i+p] ( 0 < i+p < len )的p ;
来自于其他人的做法: •知识点:KMP算法、对next数组的理解 •KMP算法中next数组的含义是什么? •next数组:失配指针 •如果目标串的当前字符i在匹配到模式串的第j个字符时失配,那么我们可以让i试着去匹配next(j) •对于模式串str,next数组的意义就是: •如果next(j)=t,那么str[1…t]=str[len-t+1…len] •我们考虑next(len),令t=next(len); •next(len)有什么含义? •P [吨1 ...] = P [称为T-1 ...仅] •那么,长度为len-next(len)的前缀显然是符合题意的。 •接下来我们应该去考虑谁? •t = next(next(len)); •t = next(next(next(len))); • 一直下去直到t=0,每个符合题意的前缀长是len-t
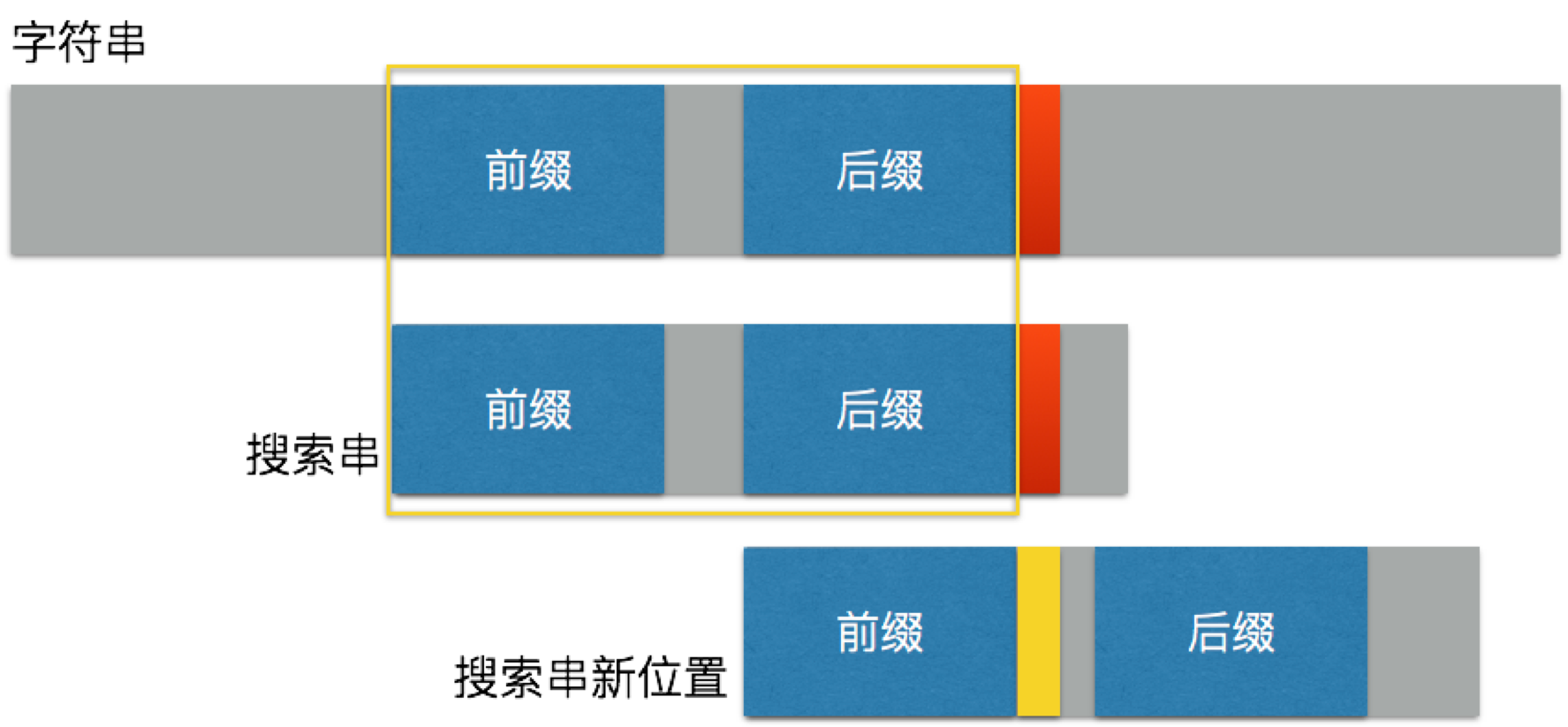
这时我们通过查询部分匹配表可以知道,黄色框内的字符串存在一个相同的前缀和后缀。那么结论就很明显了,我们完全可以将搜索串移动更长的距离,使其前缀与字符串中的后缀相对应,而新的检索位从黄色字符对应的位置开始即可。这样我们就充分利用之前的已知信息,减少了对比次数
现在,我们再看一下如何编程快速求得next数组。其实,求next数组的过程完全可以看成字符串匹配的过程,即以模式字符串为主字符串,以模式字符串的前缀为目标字符串,一旦字符串匹配成功,那么当前的next值就是匹配成功的字符串的长度。
具体来说,就是从模式字符串的第一位(注意,不包括第0位)开始对自身进行匹配运算。 在任一位置,能匹配的最长长度就是当前位置的next值。如下图所示。
从上面的分析和代码可以看出,KMP方法对于那些有前后缀的pattern效果比较明显。如果pattern本身或者它的子字符串没有相同的前后缀,既部分匹配表的值都为0,那么KMP就会退化为暴力搜索的形式,比如当字符串为’aaaaaa’,而搜索串为’ab’时,每一次搜索串都只会向后移动一位而已。