HDU 1011 Starship Troopers【树形DP/有依赖的01背包】

You, the leader of Starship Troopers, are sent to destroy a base of the bugs. The base is built underground. It is actually a huge cavern, which consists of many rooms connected with tunnels. Each room is occupied by some bugs, and their brains hide in some of the rooms. Scientists have just developed a new weapon and want to experiment it on some brains. Your task is to destroy the whole base, and capture as many brains as possible. 

To kill all the bugs is always easier than to capture their brains. A map is drawn for you, with all the rooms marked by the amount of bugs inside, and the possibility of containing a brain. The cavern's structure is like a tree in such a way that there is one unique path leading to each room from the entrance. To finish the battle as soon as possible, you do not want to wait for the troopers to clear a room before advancing to the next one, instead you have to leave some troopers at each room passed to fight all the bugs inside. The troopers never re-enter a room where they have visited before. 

A starship trooper can fight against 20 bugs. Since you do not have enough troopers, you can only take some of the rooms and let the nerve gas do the rest of the job. At the mean time, you should maximize the possibility of capturing a brain. To simplify the problem, just maximize the sum of all the possibilities of containing brains for the taken rooms. Making such a plan is a difficult job. You need the help of a computer. 

InputThe input contains several test cases. The first line of each test case contains two integers N (0 < N <= 100) and M (0 <= M <= 100), which are the number of rooms in the cavern and the number of starship troopers you have, respectively. The following N lines give the description of the rooms. Each line contains two non-negative integers -- the amount of bugs inside and the possibility of containing a brain, respectively. The next N - 1 lines give the description of tunnels. Each tunnel is described by two integers, which are the indices of the two rooms it connects. Rooms are numbered from 1 and room 1 is the entrance to the cavern. 

The last test case is followed by two -1's. 
OutputFor each test case, print on a single line the maximum sum of all the possibilities of containing brains for the taken rooms. 
Sample Input

5 10
50 10
40 10
40 20
65 30
70 30
1 2
1 3
2 4
2 5
1 1
20 7
-1 -1

Sample Output

50
7

 

 

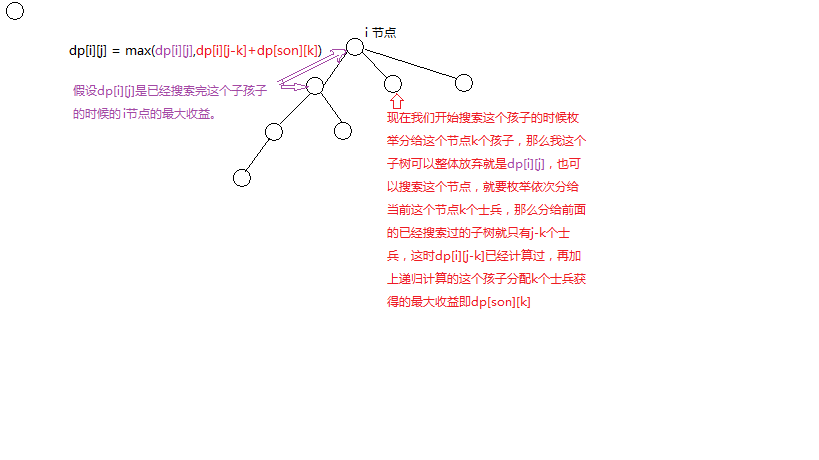
#include<cstdio>
#include<string>
#include<cstdlib>
#include<cmath>
#include<iostream>
#include<cstring>
#include<set>
#include<queue>
#include<algorithm>
#include<vector>
#include<map>
#include<cctype>
#include<stack>
#include<sstream>
#include<list>
#include<assert.h>
#include<bitset>
#include<numeric>
#define debug() puts("++++")
#define gcd(a,b) __gcd(a,b)
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
#define fi first
#define se second
#define pb push_back
#define sqr(x) ((x)*(x))
#define ms(a,b) memset(a,b,sizeof(a))
#define sz size()
#define be begin()
#define pu push_up
#define pd push_down
#define cl clear()
#define lowbit(x) -x&x
#define all 1,n,1
#define rep(i,x,n) for(int i=(x); i<=(n); i++)
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int,int> P;
const int INF = 0x3f3f3f3f;
const LL LNF = 1e18;
const int maxm = 1e6 + 10;
const double PI = acos(-1.0);
const double eps = 1e-8;
const int dx[] = {-1,1,0,0,1,1,-1,-1};
const int dy[] = {0,0,1,-1,1,-1,1,-1};
int dir[4][2] = {{0,1},{0,-1},{-1,0},{1,0}};
const int mon[] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int monn[] = {0, 31, 29, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
const int mod = 10056;
#define inf 0x3f3f3f3f
#define ll long long
const int maxn = 1e4+5;
int t,n,m,x,y;
int dp[maxn][150],p[maxn],b[maxn];
int cost[maxn];
struct node
{
    int u,v,nxt;
}e[maxn*2];
int head[maxn];
int tot=0;
void init()
{
    ms(head,-1);
    ms(dp,0);
}
void add(int u,int v)
{
    e[tot].v=v;
    e[tot].nxt=head[u];
    head[u]=tot++;
}
void dfs(int u,int fa)
{
    for(int i=cost[u];i<=m;i++)
        dp[u][i]=p[u]; //小于cost的无法获得经验 - dp[i][1]=val;
    for(int i=head[u]; i!=-1; i=e[i].nxt) //相当于背包种类
    {
        int v=e[i].v;
        if(v==fa) continue;
        dfs(v,u);
        for(int j=m; j>=cost[u]; j--) //祖先的人力范围
        {
            for(int k=1; k<=j-cost[u]; k++) //子树的人力范围
            {
                dp[u][j]=max(dp[u][j],dp[u][j-k] + dp[v][k]);
            }
        }
    }
}
int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        if(n==-1&&m==-1) break;
        init();
        for(int i=1;i<=n;i++)
        {
            scanf("%d %d",&b[i],&p[i]);
            cost[i]=(b[i]+19)/20; //花费人力
        }
        for(int i=1;i<n;i++)
        {
            scanf("%d %d",&x, &y);
            add(x,y);
            add(y,x);
        }
        if(!m)
        {
            printf("0\n");continue;
        }
        dfs(1,-1);
        printf("%d\n",dp[1][m]);
    }
}
/*

【题意】
给你n和m代表n个点，m个士兵，要到下一个房间必须攻破上一个房间，每个士兵最多消灭20个BUG，就算不足20个BUG也要安排一个士兵
以1点为源点，向相邻的点移动，每个点有一个代价(值/20)和价值。
求花费m的士兵得到的最大价值是多少。

就是：给定一棵树，从1号顶点进入树中，每次可以分配人到其他可达的顶点去，杀死所有的bugs可以获取brain值，求出m个人最多能获取多少brain值。
【类型】
树形DP

【分析】
一看到价值和代价同时出现，马上想到背包，而且是有限的物品(结点)，那么是01背包。
看出这是一棵树，那么就是树形01背包，对于树形DP自有一套应对方法。
设dp[i][j]：以i为根的子树有j个士兵的时候最多获得的价值。
转移方程：
dp[i][j] = max(dp[i][j], dp[i][j-k] + dp[son(i)][k]);

【时间复杂度&&优化】

【trick】
分析的时候自顶向下，实现自底向上，这也是dfs的思想，树形dp一般都是在dfs过程中实现的

【数据】

*/