7/31 CSU-ACM2018暑期训练7-贪心
比赛链接
A-CSU - 1588
现在有n堆果子,第i堆有ai个果子。现在要把这些果子合并成一堆,每次合并的代价是两堆果子的总果子数。求合并所有果子的最小代价。
Input
第一行包含一个整数T(T<=50),表示数据组数。
每组数据第一行包含一个整数n(2<=n<=1000),表示果子的堆数。
第二行包含n个正整数ai(ai<=100),表示每堆果子的果子数。
Output
每组数据仅一行,表示最小合并代价。
Sample Input
2
4
1 2 3 4
5
3 5 2 1 4
Sample Output
19
33
【分析】:使用优先队列,注意cmp是小的优先,所以是priority_queue<int,vector
1.把果子都push进q内;
2.当q的size大于1,不断取最小的两个top相加,如何取呢?当取完一个top就pop掉,那么剩下的那个顶替为最小,合并就是把这两个之和push进q,然后记录a+b权值的和
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define test freopen("test.txt","r",stdin)
#define maxn 1000005
#define mod 10007
#define eps 1e-5
const int inf=0x3f3f3f3f;
const ll infll = 0x3f3f3f3f3f3f3f3fLL;
int n,x;
int t,sum[maxn];
int ans,a,b;
int main()
{
scanf("%d",&t);
while(t--)
{
priority_queue<int,vector<int>,greater<int> > q;
while(!q.empty()) q.pop();
ans=0;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&x);
q.push(x);
}
while(q.size()!=1)
{
a=q.top();
q.pop();
b=q.top();
q.pop();
q.push(a+b);
ans+=a+b;
}
cout<<ans<<endl;
}
}
B-HDU - 1789

【题意】:给出n个作业的截止日期,和n个作业不交所扣掉的分数,要求输出扣除分数做少的方案。
【分析】:已知扣分和截止日期,要求扣分最少。那么我按扣分由大到小排序,分数相同则截止日期由短到长排序。
为什么呢?因为我们最终目的是扣分最少,那么扣分权重大的自然要尽快完成,以免超过dd(deadline)而扣很大,扣分分数相同的话dd由短到长排序,自然是为了将马上就要交的作业先完成。总而言之,就是要优先考虑:扣分多、急着交的作业。
贪心策略是:
1.扣除分数大的先做
2.扣除分数相同,时间先截止的先做
3.做一件事的时候,从截止时间从后往前开始向第一天遍历,如果当天没有被作业占据则标记为占据。做这件事的日期越大越靠后越好。为什么呢?因为留给dd短的时间的余地就多些。
4.如果不能满足3的条件,则为不能完成
7
1 4 6 4 2 4 3
3 2 1 7 6 5 4
------------------
After Sort:
4 7
2 6
4 5
3 4
1 3
4 2
6 1
-------------------
j = 4
j = 2
j = 3
j = 1
j = 0
day = 1 score = 3
j = 0
day = 4 score = 2
j = 6
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define test freopen("test.txt","r",stdin)
#define maxn 1000005
#define mod 10007
#define eps 1e-5
const int inf=0x3f3f3f3f;
const ll infll = 0x3f3f3f3f3f3f3f3fLL;
int n,x,t,sum,j,d;
int vis[maxn];
struct node
{
int day;
int score;
}a[maxn];
bool cmp(node a,node b)
{
return a.score>b.score;
return a.day<b.day;
}
int main()
{
scanf("%d",&t);
while(t--)
{
memset(vis,0,sizeof(vis));
scanf("%d",&n);
for(int i=0;i<n;i++)
scanf("%d",&a[i].day);
for(int i=0;i<n;i++)
scanf("%d",&a[i].score);
sort(a,a+n,cmp);
sum=0;
for(int i=0;i<n;i++)
{
d=a[i].day;
for(j=d;j>0;j--)
{
if(!vis[j])
{
vis[j]=1;
break;
}
}
if(!j) sum+=a[i].score;
}
printf("%d\n",sum);
}
}
C-UVA - 11572
【题意】:求一个数组连续子区间内元素都不相同时的最大区间长度。
Output
For each test case output a line containing single integer, the maximum number of unique snowflakes
that can be in a package.
Sample Input
1
5
1
2
3
2
1
Sample Output
3
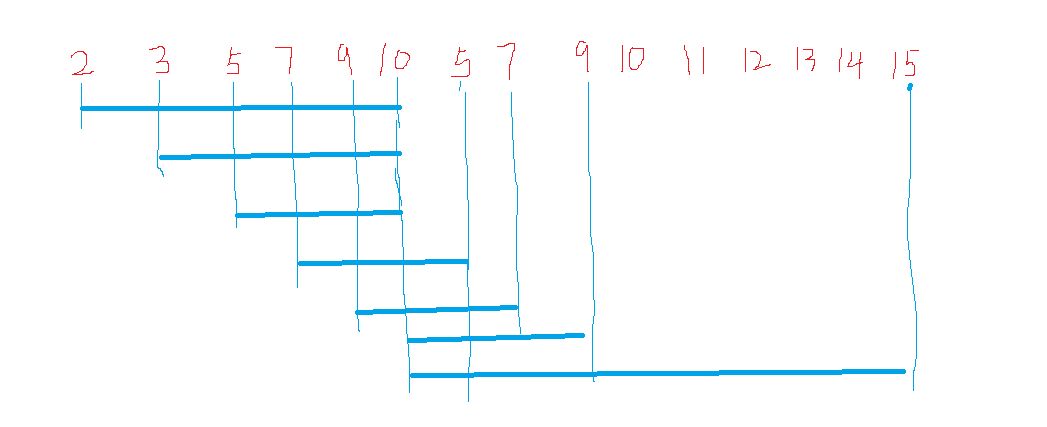
【分析】:双指针。设置L和R两个指针。O(nlogn)
1.L和R都指向第一个元素,设置Max记录区间最长长度。
2.当遇到没出现过的元素并且R指针在数组内,把R指向元素加入set同时R右移一位。(即延伸右端点)
3.打擂台算法记录区间最长长度。
4.R滑不动了,说明出现相同元素,删掉无用元素,并且左端点L后移。
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define test freopen("test.txt","r",stdin)
#define maxn 1000005
#define mod 10007
#define eps 1e-5
const int inf=0x3f3f3f3f;
const ll infll = 0x3f3f3f3f3f3f3f3fLL;
int n,x,t,sum,j,d;
int a[maxn];
int main()
{
scanf("%d",&t);
while(t--)
{
set<int> s;
s.clear();
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&a[i]);
}
int L=0,R=0,Max=0;
while(R<n)
{
while(R<n && !s.count(a[R]))//R持续向右滑动
{
s.insert(a[R++]);
}
Max=max(Max,R-L);
s.erase(a[L++]);//R滑不动了,则L向后移动一位后试试
}
cout<<Max<<endl;
}
}
D-POJ - 1328 【区间选点问题】:紫书P233
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2
1 2
-3 1
2 1
1 2
0 2
0 0
Sample Output
Case 1: 2
Case 2: 1
【题意】:假设海岸线是一条无限延伸的直线。它的一侧是陆地,另一侧是海洋。每一座小岛是在海面上的一个点。雷达必须安装在陆地上(包括海岸线),并且每个雷达都有相同的扫描范围d。你的任务是建立尽量少的雷达站,使所有小岛都在扫描范围之内。
数据使用笛卡尔坐标系,定义海岸线为x轴。在x轴上方为海洋,下方为陆地。
【分析】:https://www.luogu.org/problemnew/show/P1325
//这题本质上是一个区间取点问题
//采用贪心策略
//题目中说雷达必须安装在陆地上(包括海岸线)我们可以很容易地想到,雷达站一定要建在海岸线上
//因为对于每一个不在海岸线上的雷达站A,和它横坐标相同的海岸线上的雷达站B的海面探测范围一定包含A的探测范围
//所以选海岸线上的点一定优于不在海岸线上的点
//题目要求每一个岛屿都要覆盖到,不能遗漏
//而雷达的探测距离为d,所以一个雷达想要探测到它,则必须和他的距离小于等于d
//所以用勾股定理推出探测到一个岛屿I(x,y)的海岸线区间为[x-sqrt(d*d-y*y),x+sqrt(d*d-y*y)]
//这样每个岛屿都对应一个区间,我们需要在x轴上取尽量少的点使每个区间上都至少有一个点
//于是我们就把这道题转换成了一个区间取点问题(参见 刘汝佳《算法竞赛入门经典(第二版)》P233)
//把所有区间按右端点升序排序,如果右端点相同则按左端点降序排序,开始贪心
//在第一个区间[a,b]取点时取第一个区间的右端点一定最优。因为选的点在[a,b)中,包含此点的区间比在b上多
//遍历所有区间,每次取当前区间的右端点建立雷达站,这个点记为nx,ans++;
//若nx包含在当前区间,则继续遍历下一个区间,否则nx更新为当前区间的右端点,ans++;
//printf("%d\n",ans);
//若一个点的y大于d则无论如何也探测不到它,输出-1,结束
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define test freopen("test.txt","r",stdin)
#define mod 10007
#define eps 1e-6
double pi = acos(-1.0);
const int MAXN = 5e4 + 5;
int n;
double d;
struct node
{
double left, right;
}a[1010];
bool cmp(const node& n1, const node& n2)
{
return n1.right < n2.right || (n1.right == n2.right && n1.left > n2.left);
}
int cal(double pos)
{
int ans = 1;
for(int i = 1; i < n; ++i)
{
if(a[i].left > pos)
{
pos = a[i].right;
ans++;
}
}
return ans;
}
int main()
{
int t = 0;
int flag = 0;
while(scanf("%d%lf",&n,&d) != EOF && (n + d))
{
flag = 0;
double x, y;
for(int i = 0; i < n; ++i)
{
scanf("%lf%lf",&x,&y);
if(y > d)
{
flag = 1;
}
a[i].left = x - sqrt(d*d - y*y);
a[i].right = x + sqrt(d*d - y*y);
}
if(flag)
{
printf("Case %d: %d\n",++t,-1);
}
else
{
sort(a, a+n, cmp);
printf("Case %d: %d\n",++t,cal(a[0].right));
}
}
}
E-POJ - 1521
题目描述
输入一个字符串,长度不超过100,仅由大写字母和下划分组成。求用最好的字符编码方式,令总长度最小。
输入
多组数据,每组数据在一行上输入一个字符串,格式如前所述
当遇到END时,表示输入结束
输出
对应每个输入,在一行上输出3个信息:首先是每个字母按固定长度8bit编码,字符串的总长度,然后是按最优编码的总长度,最后是前者对后者的比率,保留1位小数。
样例输入
AAAAABCD
THE_CAT_IN_THE_HAT
END
样例输出
64 13 4.9
144 51 2.8
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define test freopen("test.txt","r",stdin)
#define maxn 1000005
#define mod 10007
#define eps 1e-5
const int inf=0x3f3f3f3f;
const ll infll = 0x3f3f3f3f3f3f3f3fLL;
int n,x,t,sum,a,b;
char str[1500];
int cnt[27];
int main()
{
int n,m,a,b,sum;
while(scanf("%s",str),strcmp(str,"END")!=0)
{
memset(cnt,0,sizeof(cnt));
n=strlen(str);
for(int i=0;i<n;i++)
{
if(str[i]!='_')
cnt[str[i]-'A']++;
else
cnt[26]++;
}
priority_queue<int,vector<int>,greater<int> > q;
for(int i=0;i<=26;i++)
if(cnt[i]!=0)
q.push(cnt[i]);
sum=0;
while(q.size()>1)
{
a=q.top();
q.pop();
b=q.top();
q.pop();
q.push(a+b);
sum+=(a+b);
}
if(sum==0) sum=n;
printf("%d %d %.1f\n",n*8,sum,(n*8.0)/(sum*1.0));
}
return 0;
}
F-POJ - 3122 [二分]
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define test freopen("test.txt","r",stdin)
#define maxn 1000005
#define mod 10007
#define eps 1e-6
double pi = acos(-1.0); //
const int MAXN=10010;
double s[MAXN];
double L,R;
int T,m,n,r;
double check(double mid)
{
int ret=0;
for(int i=0; i<n; i++)
ret+=(int)(s[i]/mid);
return ret >= m;
}
int main()
{
scanf("%d",&T);
while( T-- )
{
L=R=0;
scanf("%d%d",&n,&m),m++;
for(int i=0;i<n;i++)
{
scanf("%d",&r);
s[i]=pi*r*r;
R+=s[i];
}
while(R-L>eps)
{
double mid=(L+R)/2;
if( check( mid ) )
L=mid;
else
R=mid;
}
printf("%.4f\n",L);
}
return 0;
}
G-HDU - 1735
一天,淘气的Tom不小心将水泼到了他哥哥Jerry刚完成的作文上。原本崭新的作文纸顿时变得皱巴巴的,更糟糕的是由于水的关系,许多字都看不清了。可怜的Tom知道他闯下大祸了,等Jerry回来一定少不了一顿修理。现在Tom只想知道Jerry的作文被“破坏”了多少。
Jerry用方格纸来写作文,每行有L个格子。(图1显示的是L = 10时的一篇作文,’X’表示该格有字,该文有三个段落)。
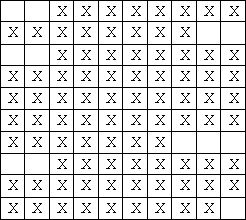
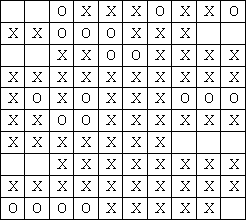
图2显示的是浸水后的作文 ,‘O’表示这个位置上的文字已经被破坏。可是Tom并不知道原先哪些格子有文字,哪些没有,他唯一知道的是原文章分为M个段落,并且每个段落另起一行,空两格开头,段落内部没有空格(注意:任何一行只要开头的两个格子没有文字就可能是一个新段落的开始,例如图2中可能有4个段落)。
Tom想知道至少有多少个字被破坏了,你能告诉他吗?
Input
测试数据有多组。每组测试数据的第一行有三个整数:N(作文的行数1 ≤ N ≤ 10000),L(作文纸每行的格子数10 ≤ L ≤ 100),M(原文的段落数1 ≤ M ≤ 20),用空格分开。
接下来是一个N × L的位矩阵(A ij)(相邻两个数由空格分开),表示被破坏后的作文。其中Aij取0时表示第i行第j列没有文字(或者是看不清了),取1时表示有文字。你可以假定:每行至少有一个1,并且所有数据都是合法的。
Output
对于每组测试输出一行,一个整数,表示至少有多少文字被破坏。
Sample Input
10 10 3
0 0 0 1 1 1 0 1 1 0
1 1 0 0 0 1 1 1 0 0
0 0 1 1 0 0 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 0 1 0 1 1 1 0 0 0
1 1 0 0 1 1 1 1 1 1
1 1 1 1 1 1 1 0 0 0
0 0 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
0 0 0 0 1 1 1 1 1 0
Sample Output
19
【分析】:
首先将所有为0的地方统计,因为是求最小的字数,所有最后一行后面的0可以看为空格直接减掉,
因为有m段(一定包括第一行),再减去m*2,最后枚举每行,将至少前两个为0的上一行的最后有多少
的0统计起来排序,再依次减去前m-1个大的,这样就保证了得到的答案是符合条件中最小的
#include <cstdio>
#include <cmath>
#include <cstring>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>
#include <sstream>
#include <queue>
#include <typeinfo>
#include <fstream>
#include <map>
#include <stack>
typedef long long ll;
using namespace std;
#define sspeed ios_base::sync_with_stdio(0);cin.tie(0)
#define test freopen("test.txt","r",stdin)
#define mod 10007
#define eps 1e-6
double pi = acos(-1.0);
const int MAXN = 1e5 + 5;
int n,m,k,x;
int a[MAXN][150];
int r[MAXN];
bool cmp(int x,int y)
{
return x>y;
}
int main()
{
while(~scanf("%d%d%d",&n,&m,&x))
{
int sum=0,ans,flag;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
if(!a[i][j]) sum++;
}
}
for(int i=m;i>=1;i--)
{
if(!a[n][i]) sum--;
else break; //00001100
}
k=1;
for(int i=2;i<=n;i++)
{
ans=0;flag=0;
if(!a[i][1] && !a[i][2]) //00开头
{
flag=1;
for(int j=m;j>=1;j--)
{
if(!a[i-1][j])
ans++;
else
break;
}
}
if(flag)
r[k++]=ans;
}
sum -= 2*x;
x--;
sort(r+1,r+k,cmp);
for(int i=1; i<=x; i++)
sum -= r[i];
printf("%d\n",sum);
}
}
H - 地区500强 HDU - 4864
Today the company has m tasks to complete. The ith task need xi minutes to complete. Meanwhile, this task has a difficulty level yi. The machine whose level below this task’s level yi cannot complete this task. If the company completes this task, they will get (500xi+2yi) dollars.
The company has n machines. Each machine has a maximum working time and a level. If the time for the task is more than the maximum working time of the machine, the machine can not complete this task. Each machine can only complete a task one day. Each task can only be completed by one machine.
The company hopes to maximize the number of the tasks which they can complete today. If there are multiple solutions, they hopes to make the money maximum.
Input
The input contains several test cases.
The first line contains two integers N and M. N is the number of the machines.M is the number of tasks(1 < =N <= 100000,1<=M<=100000).
The following N lines each contains two integers xi(0<xi<1440),yi(0=<yi<=100).xi is the maximum time the machine can work.yi is the level of the machine.
The following M lines each contains two integers xi(0<xi<1440),yi(0=<yi<=100).xi is the time we need to complete the task.yi is the level of the task.
Output
For each test case, output two integers, the maximum number of the tasks which the company can complete today and the money they will get.
Sample Input
1 2
100 3
100 2
100 1
Sample Output
1 50004
【分析】:贪心。题目很特别的给出了获得金钱的计算公式为500x+2y,y<=100,所以可以按任务时间从大到小排序,然后每个任务找出大于该任务难度且与难度最接近的机器完成该任务。
#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <set>
#include <map>
#include <queue>
#define PI acos(-1.0)
#define eps 1e-6
typedef __int64 LL;
typedef long double LD;
using namespace std;
const int maxn=1e5+10;
int n,m;
/*
*/
struct node
{
int x,y;
}a[maxn],b[maxn];
int c[105];
int cmp(node a,node b)
{
if(a.x == b.x)
return a.y>b.y;
return a.x>b.x;
}
int main()
{
int num;
LL sum=0;
while(~scanf("%d%d",&n,&m))
{
for(int i=0;i<n;i++)
scanf("%d%d",&a[i].x, &a[i].y);
for(int i=0;i<m;i++)
scanf("%d%d",&b[i].x, &b[i].y);
sort(a,a+n,cmp);
sort(b,b+m,cmp);
num=sum=0;
memset(c,0,sizeof(c));
for(int i=0,j=0; i<m; i++)
{
//取机器的游标j,j表示所有机器中能完成该任务的下限机器,每次从当前j开始寻找最合适的j。
while(j<n && a[j].x >= b[i].x)//找能完成的用时最少的,后面肯定都能满足
{
c[a[j].y]++;//j停在最小的不会重复
j++;
}
//选lev最小的,每个lev有几个符合的即可,前面符合后面一定也可以用
for(int k = b[i].y; k<=100; k++)
{
if(c[k])
{
c[k]--;
sum+=( 500*b[i].x + 2*b[i].y );
num++;
break;
}
}
}
printf("%d %I64d\n",num,sum);
}
}
I - 龙之队 HYSBZ - 4198
追逐影子的人,自己就是影子。 ——荷马
Allison 最近迷上了文学。她喜欢在一个慵懒的午后,细细地品上一杯卡布奇诺,静静地阅读她爱不释手的《荷马史诗》。但是由《奥德赛》和《伊利亚特》组成的鸿篇巨制《荷马史诗》实在是太长了,Allison 想通过一种编码方式使得它变得短一些。
一部《荷马史诗》中有 n 种不同的单词,从 1 到 n 进行编号。其中第 i 种单词出现的总次数为 wi。Allison 想要用 k 进制串 si 来替换第 i 种单词,使得其满足如下要求:
对于任意的 1≤i,j≤n,i≠j,都有:si 不是 sj 的前缀。
现在 Allison 想要知道,如何选择 si,才能使替换以后得到的新的《荷马史诗》长度最小。在确保总长度最小的情况下,Allison 还想知道最长的 si 的最短长度是多少?
一个字符串被称为 k 进制字符串,当且仅当它的每个字符是 0 到 k−1 之间(包括 0 和 k−1)的整数。
字符串 Str1 被称为字符串 Str2 的前缀,当且仅当:存在 1≤t≤m,使得 Str1=Str2[1..t]。其中,m 是字符串 Str2 的长度,Str2[1..t] 表示 Str2 的前 t 个字符组成的字符串。
Input
输入文件的第 1 行包含 2 个正整数 n,k,中间用单个空格隔开,表示共有 n 种单词,需要使用 k 进制字符串进行替换。
接下来 n 行,第 i+1 行包含 1 个非负整数 wi,表示第 i 种单词的出现次数。
Output
输出文件包括 2 行。
第 1 行输出 1 个整数,为《荷马史诗》经过重新编码以后的最短长度。
第 2 行输出 1 个整数,为保证最短总长度的情况下,最长字符串 si 的最短长度。
Sample Input
4 2
1
1
2
2
Sample Output
12
2
Hint
用 X(k) 表示 X 是以 k 进制表示的字符串。
一种最优方案:令 00(2) 替换第 1 种单词,01(2) 替换第 2 种单词,10(2) 替换第 3 种单词,11(2) 替换第 4 种单词。在这种方案下,编码以后的最短长度为:
1×2+1×2+2×2+2×2=12
最长字符串 si 的长度为 2。
一种非最优方案:令 000(2) 替换第 1 种单词,001(2) 替换第 2 种单词,01(2) 替换第 3 种单词,1(2) 替换第 4 种单词。在这种方案下,编码以后的最短长度为:
1×3+1×3+2×2+2×1=12
最长字符串 si 的长度为 3。与最优方案相比,文章的长度相同,但是最长字符串的长度更长一些。
对于所有数据,保证 2≤n≤100000,2≤k≤9。
选手请注意使用 64 位整数进行输入输出、存储和计算。
【分析】:k叉哈夫曼树。
依据题意和题目背景里面的一些暗示,思路可以明确,就是要求构造一个K进制的哈夫曼编码。平时我们所说的哈夫曼编码为2进制的,构造的方法也很容易(类似于NOIP2004 合并果子),本题也可以使用相同的思想。
首先明确需要维护什么。转换一下题意,不难知道我们需要维护的是最短的带权路径之和和该哈夫曼树的高度。然后便是如何维护,由于不需要知道哈夫曼树的具体形态,我们便可以按照哈夫曼树的构造方式,将当前最小的K个节点合并为1个父节点,直至只有一个父节点。看到“将最小K个节点合并”便可以明确使用优先队列(二叉堆)进行维护。
最后,我们需要注意一个细节。因为每次都是将k个节点合并为1个(减少k-1个),一共要将n个节点合并为1个,如果(n-1)%(k-1)!=0 则最后一次合并时不足k个。也就表明了最靠近根节点的位置反而没有被排满,因此我们需要加入k-1-(n-1)%(k-1)个空节点使每次合并都够k个节点(也就是利用空节点将其余的节点挤到更优的位置上)。
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
#include <ext/pb_ds/priority_queue.hpp> //pb_ds库
#define LL long long
using namespace std;
struct node{
LL w,h;
node(LL W, LL H){
w=W,h=H;
}
};
bool operator<(node a, node b){
if(a.w!=b.w) return a.w>b.w;
return a.h>b.h; //如果长度相等,高度小的优先
} //构造小根堆的操作。
__gnu_pbds::priority_queue <node, std::less<node>, __gnu_pbds::pairing_heap_tag> q; //优先队列
int n,k,cnt;
LL temp,maxh,ans;
int main()
{
scanf("%d%d",&n,&k);
for(int i=1; i<=n; i++){
scanf("%lld",&temp);
q.push(node(temp,1));
}
if((n-1)%(k-1) != 0) cnt=k-1-(n-1)%(k-1); //判断是否要补空节点
for (int i=1; i<=cnt; i++)
q.push(node(0,1)); //补空节点
cnt+=n; //cnt为根节点个数(最初每个根节点都为其本身)
while(cnt>1){
temp=maxh=0;
for(int i=1; i<=k; i++){
temp+=q.top().w;
maxh=max(maxh,q.top().h);
q.pop();
}
ans+=temp; //维护带权路径长度之和
q.push(node(temp, maxh+1)); //合并,高度为最高子树高度+1
cnt-=k-1; //减少根节点
}
printf("%lld\n%lld\n",ans,q.top().h-1);
return 0;
}
51Nod-1205-流水线调度/POJ2751
Johnson算法:
(1) 把作业按工序加工时间分成两个子集,第一个集合中在S1上做的时间比在S2上少,其它的作业放到第二个集合。先完成第一个集合里面的作业,再完成第二个集合里的作业。
(2) 对于第一个集合,其中的作业顺序是按在S1上的时间的不减排列;对于第二个集合,其中的作业顺序是按在S2上的时间的不增排列。
#include <bits/stdc++.h>
using namespace std;
struct node
{
int a,b;
};
vector<node> p,s;
int cmpp(const node& a, const node& b)
{
return a.a < b.a;
}
int cmps(const node& a, const node& b)
{
return a.b > b.b;
}
int main()
{
int n;
node tn;
scanf("%d",&n);
for(int i = 0; i < n; ++i)
{
scanf("%d %d",&tn.a,&tn.b);
if(tn.b > tn.a) p.push_back(tn);
else s.push_back(tn);
}
sort(p.begin(),p.end(),cmpp);
sort(s.begin(),s.end(),cmps);
p.insert(p.end(),s.begin(),s.end());
int res = p[0].a+p[0].b;
int sum = p[0].a;
for(int i = 1; i < p.size(); ++i)
{
sum += p[i].a;
res = sum < res ? res+p[i].b:sum+p[i].b;
}
printf("%d\n",res);
return 0;
}


