LOJ N！在不同进制的位数

lightoj1045 - Digits of Factorial (N！不同进制的位数)

对于一个B进制的数，只需要对其取以B的对数就可以得到他在B进制情况下的位数(取了对数之后可能为小数，所以还需要取整后再+1)

—  N ! 的位数就是  [lg(N!)]+1=[lg(1)+lg(2)+…+lg(N)]+1

—= (int) ceil[(n*ln(n)-n+0.5*ln(2*n*π))/ln(10)]      /*ceil是向上取整,[]符号为取整*/

—   最后一个式子被称为斯特林公式

 

 

 

cin>>n;
cout<<(int)(ceil((n*log(n)-n+0.5*log(2*n*pi))/log(10)))<<endl;

 

---

 

 

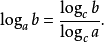【换底公式：logx (n!) = log(n!) /  log(x) 】

 

  【阶乘变加法：log (n!)=log1 + log2 + log3 + log4 +……+log(n),】

 

N !在10进制下的位数为log10 (n!) + 1;  所以在x进制下的位数为logx (n!) + 1;

但是计算机只能表示以10和e为底的对数，所以要用换底公式，logx (n!) = log(n!) /  log(x) ;【注意，等号右边的 log 都是默认以e为底】

log (n!)=log1 + log2 + log3 + log4 +……+log(n), 所以n比较大时计算log(n!)时已经把其他数的阶乘也算出来了，

如果给出一个n都要计算阶乘的话，费时间o(n),所以可以把 log (n!) 先用double型数组sum[]先存起来，令sun[i]=log(i!)

先预处理出sum[i]后面可直接调用；

#include<stdio.h>  
#include<string.h>  
#include<math.h>  
double sum[1000009];//数组要是double型的；   
int main()  
{  
    memset(sum,0,sizeof(sum));  
    sum[1]=log(1);  
    for(int i=2;i<=1000000;i++)  
    {  
        sum[i]=sum[i-1]+log(i);  
    }  
    int t,n,b,mm=1;  
    scanf("%d",&t);  
    while(t--)  
    {  
        scanf("%d%d",&n,&b);  
        if(n==0)  
        {  
            printf("Case %d: 1\n",mm++);//0的阶乘等于1，此时不能用sum[0],因为真数不能为0不符合所以要单独列出；   
        }  
        else  
        {  
            int c;//定义一个整形c,把double强制转换成int ;  
            c=sum[n]/log(b)+1;  
            printf("Case %d: %d\n",mm++,c);  
        }  
    }  
    return 0;  
}