洛谷 P1784 数独[DFS/回溯]
To 洛谷.1784 数独 类似题:CODEVS.4966 简单数独(4*4数独) CODEVS.2924 数独挑战)
题目描述
数独是根据9×9盘面上的已知数字,推理出所有剩余空格的数字,并满足每一行、每一列、每一个粗线宫内的数字均含1-9,不重复。每一道合格的数独谜题都有且仅有唯一答案,推理方法也以此为基础,任何无解或多解的题目都是不合格的。
芬兰一位数学家号称设计出全球最难的“数独游戏”,并刊登在报纸上,让大家去挑战。
这位数学家说,他相信只有“智慧最顶尖”的人才有可能破解这个“数独之谜”。
据介绍,目前数独游戏的难度的等级有一道五级,一是入门等级,五则比较难。不过这位数学家说,他所设计的数独游戏难度等级是十一,可以说是所以数独游戏中,难度最高的等级他还表示,他目前还没遇到解不出来的数独游戏,因此他认为“最具挑战性”的数独游戏并没有出现。
输入输出格式
输入格式:
一个未填的数独
输出格式:
填好的数独
输入输出样例
8 0 0 0 0 0 0 0 0 0 0 3 6 0 0 0 0 0 0 7 0 0 9 0 2 0 0 0 5 0 0 0 7 0 0 0 0 0 0 0 4 5 7 0 0 0 0 0 1 0 0 0 3 0 0 0 1 0 0 0 0 6 8 0 0 8 5 0 0 0 1 0 0 9 0 0 0 0 4 0 0
8 1 2 7 5 3 6 4 9 9 4 3 6 8 2 1 7 5 6 7 5 4 9 1 2 8 3 1 5 4 2 3 7 8 9 6 3 6 9 8 4 5 7 2 1 2 8 7 1 6 9 5 3 4 5 2 1 9 7 4 3 6 8 4 3 8 5 2 6 9 1 7 7 9 6 3 1 8 4 5 2
[分析]:
用三个数组进行标记每行、每列、每个子网格已用的数字,用于剪枝
bool row[10][10]; //row[i][x] 标记在第i行中数字x是否出现了
bool col[10][10]; //col[j][y] 标记在第j列中数字y是否出现了
bool g[10][10]; //g[k][x] 标记在第k个3*3子格中数字z是否出现了
row 和 col的标记比较好处理,关键是找出g子网格的序号与 行i列j的关系
即要知道第i行j列的数字是属于哪个子网格的
首先我们假设子网格的序号如下编排:
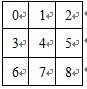
由于1<=i、j<=9,我们有: (其中“/”是C++中对整数的除法)
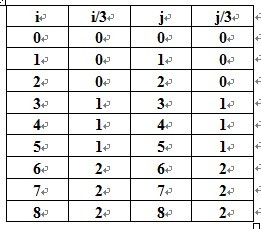
令a= i/3 , b= j/3 ,根据九宫格的 行列 与 子网格 的 关系,我们有:
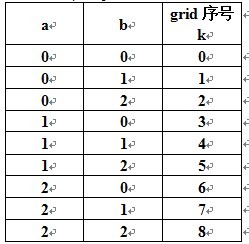
不难发现 3a+b=k
即 3*(i/3)+j/3=k
又我在程序中使用的数组下标为 1~9,grid编号也为1~9
因此上面的关系式可变形为 3*((i-1)/3)+(j-1)/3+1=k(第k个3*3子格中)
这样我们就能记录k个3*3子格中数字z是否出现了:
[代码]:

#include<cstdio> #include<cstring> #include<cstdlib> int a[10][10]; bool h[10][10],l[10][10],g[10][10];//行,列,第几个格子 void print()//输出函数 { for(int i=1;i<=9;i++) { for(int j=1;j<=9;j++) printf("%d ",a[i][j]); printf("\n"); } exit(0); } void dfs(int x,int y)//深搜 { if(a[x][y]!=0)//9*9中不为零的数直接跳过 { if(x==9&&y==9) print(); //搜索结束后输出 if(y==9) //行到顶端后搜索列 dfs(x+1,1); else //搜索行 dfs(x,y+1); } if(a[x][y]==0)//等于零时 待填数! { for(int i=1;i<=9;i++) { //true未访问过 if( h[x][i] && l[y][i] && g[(x-1)/3*3+(y-1)/3+1][i] ) //((i-1)/3)*3+(j-1)/3+1 { a[x][y]=i; //从1试到9 h[x][i]=false;//此格被占 (行) l[y][i]=false;//同上(列) g[(x-1)/3*3+(y-1)/3+1][i]=false;//同上 (格子) if(x==9&&y==9) //同a[x][y]!=0时 print(); if(y==9) dfs(x+1,1); else dfs(x,y+1); a[x][y]=0; //当前格退出返回初状态 h[x][i]=true; l[y][i]=true; g[(x-1)/3*3+(y-1)/3+1][i]=true; } } } } int main() { memset(h,true,sizeof(h)); memset(l,true,sizeof(l)); memset(g,true,sizeof(g)); for(int i=1;i<=9;i++) { for(int j=1;j<=9;j++) { scanf("%d",&a[i][j]); if(a[i][j]>0) { h[i][a[i][j]]=false;//表示格子上有数 l[j][a[i][j]]=false;//同上 g[(i-1)/3*3+(j-1)/3+1][a[i][j]]=false;//同上 } } } dfs(1,1); puts("\n"); return 0; }

/* 根据二进制的思想,用二进制的第i位是0或1来表示数字是否已出现。 用 | 运算符进行标记, 用 ^ 运算符去标记, 用 & 运算符进行判重, 这样只需要一维的数组。 */ #include<cstdio> #define z(i) (1<<i) #define g(x,y) (3*((x-1)/3)+(y-1)/3+1) int h[10],l[10],s[10],f[10][10],ok,sum=81; int read() { int _=0,___=1;char __=getchar(); while(__<'0'||__>'9'){if(__=='-')___=-1;__=getchar();} while(__>='0'&&__<='9'){_=_*10+__-'0';__=getchar();} return _*___; } void out() { for(int i=1;i<=9;i++) { for(int j=1;j<=9;j++) printf("%d ",f[i][j]); printf("\n"); } } void dfs(int x,int y,int tot) { while(f[x][y]) { y++; if(y>9) x++,y=1; } for(int i=1;i<=9;i++) { if(h[x]&z(i)||l[y]&z(i)||s[g(x,y)]&z(i)) continue; //用 & 运算符进行判重 f[x][y]=i; h[x]|=z(i); l[y]|=z(i); s[g(x,y)]|=z(i); //用 | 运算符进行标记 if(tot==sum) ok=1; else dfs(x,y,tot+1); if(ok) return ; f[x][y]=0; h[x]^=z(i); l[y]^=z(i); s[g(x,y)]^=z(i); //用 ^ 运算符去标记 } } int main() { for(int i=1;i<=9;i++) for(int x,j=1;j<=9;j++) { f[i][j]=x=read(); if(!x)continue; h[i]|=z(x); l[j]|=z(x); s[g(i,j)]|=z(x); sum--; } dfs(1,1,1); out(); return 0; }


