HDU 1568 Fibonacci【求斐波那契数的前4位/递推式】

Fibonacci

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Problem Description

2007年到来了。经过2006年一年的修炼，数学神童zouyu终于把0到100000000的Fibonacci数列
(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部给背了下来。
接下来，CodeStar决定要考考他，于是每问他一个数字，他就要把答案说出来，不过有的数字太长了。所以规定超过4位的只要说出前4位就可以了，可是CodeStar自己又记不住。于是他决定编写一个程序来测验zouyu说的是否正确。

 

Input

输入若干数字n(0 <= n <= 100000000)，每个数字一行。读到文件尾。

 

Output

输出f[n]的前4个数字（若不足4个数字，就全部输出）。

 

Sample Input

0 1 2 3 4 5 35 36 37 38 39 40

 

Sample Output

0 1 1 2 3 5 9227 1493 2415 3908 6324 1023

【分析】：

这是道神奇的题，求斐波那契数列的0到第100000000项的前四位，之前做过斐波那契数列的水题，求到63项

 

能用__int64解决，但是到100000000项的话用数组都会超时。

以下是大牛的解释：

先看对数的性质,loga(b^c)=c*loga(b),loga(b*c)=loga(b)+loga(c);
假设给出一个数10234432,那么log10(10234432)=log10(1.0234432*10^7)=log10(1.0234432)+7;

log10(1.0234432)就是log10(10234432)的小数部分.

log10(1.0234432)=0.010063744
10^0.010063744=1.023443198
那么要取几位就很明显了吧~
先取对数(对10取),然后得到结果的小数部分bit,pow(10.0,bit)以后如果答案还是<1000那么就一直乘10。
注意先处理了0~20项是为了方便。

这题要利用到数列的公式:an=(1/√5) * [((1+√5)/2)^n-((1-√5)/2)^n](n=1,2,3.....)

log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0)+log10(1-((1-√5)/(1+√5))^n)

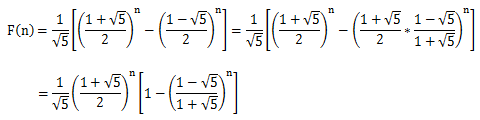
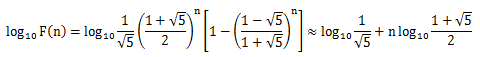
其中f=(sqrt(5.0)+1.0)/2.0;
因为log10(1-((1-√5)/(1+√5))^n)趋近于0
所以可以写成log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0);
最后取其小数部分。

而我们要取Fibonacci数的前4位，可以通过计算以10为底的对数，原理与HDU 1060 Leftmost Digit是一样的，不妨可以点开看看

另外，需要提及的一点是前20项Fibonacci数需要自己计算，一方面是因为Fibonacci数未满4位，更重要的一点是Fibonacci数较小时，公式的精确度不高

比如第17项Fibonacci应该是1597，但公式求得的是1596；而19项Fibonacci应该是4181，但公式求得的是4180

因此，我们需要先自己计算出Fibonacci数的前19项。

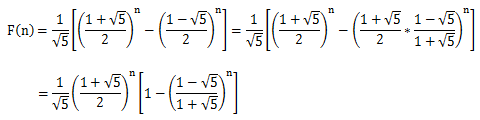
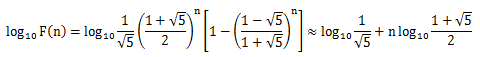
【代码】：

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 20;  
const int inf = 2147483647;  
const int mod = 2009;  
int f[N];  
int main()  
{  
    int n,i;  
    double s;  
    f[0]=0,f[1]=1;  
    for(i=2;i<N;i++)//由于接下来利用公式得出来的Fibonacci数不是精确的，越小的数则越不精确，所以前面一些Fibonacci数需要自己算  
        f[i]=f[i-1]+f[i-2];  
    while(~scanf("%d",&n))  
    {  
        if(n<N)  
        {  
            printf("%d\n",f[n]);  
            continue;  
        }  
        s=log10(1.0/sqrt(5.0))+n*log10((1+sqrt(5.0))/2);  //调用公式 
        s=s-(int)s;  //取小数部分
        s=pow(10,s);  
        while(s<1000)  //要求四位，所以要将小数点右边的数移到左边直到符合要求 
            s*=10;  
        printf("%d\n",(int)s);  
    }  
    return 0;  
}